Fixed-time group consensus of second-order multi-agent systems based on event-triggered control
2023-09-05XiaoshuaiWu武肖帅FenglanSun孙凤兰WeiZhu朱伟andrgenKurths
Xiaoshuai Wu(武肖帅), Fenglan Sun(孙凤兰),,3,†, Wei Zhu(朱伟), and Jürgen Kurths
1College of Automation,Chongqing University of Posts and Telecommunications,Chongqing 400065,China
2School of Science,Chongqing University of Posts and Telecommunications,Chongqing 400065,China
3Department of Complexity Science,Potsdam Institute for Climate Impact Research,Potsdam 14473,Germany
4Institute of Physics,Humboldt University of Berlin,Berlin 12489,Germany
Keywords: event-triggered control,group consensus,multi-agent system,fixed-time
1.Introduction
The cooperative control of multi-agent systems (MASs)has attracted many concerns in recent decades, and it has solved many important problems.The cooperative control of MASs has been widely used in traffic vehicle control,[1]formation,[2]sensor networks,[3]and other fields.[4]Among them, the consensus, which is the basic issue in the cooperative control of MASs,requires all agents in a system to finally reach the same state under a certain control protocol.
It is worth mentioning that one type of the consensus is the group consensus,[5]which means that various subgroup of a system converges to different states and the agents in the same subgroup achieve together.The group consensus theory could be applied to systems with multiple tasks.
In recent years, much attention was paid to the consensus problem for the first-order multi-agent system(MAS).[6–8]Compared with the first-order MAS, problems considered in second-order MASs[9–13]are more complex.In Ref.[6], the leader-following consensus for the first-order MAS was studied.A method of the dynamic hybrid quantizer was proposed,which overcomes the shortcomings of the static quantizer and improves the performance of the system.In Ref.[7], average consensus tracking for the first-order MAS was investigated.In Ref.[10],the second-order discrete-time MAS consensus with nonlinear terms was discussed via impulsive control.In Ref.[12],the leader-following consensus for nonlinear second-order MASs with intermittent control was studied.
It is worth noting that most of the above-mentioned works are concerned with asymptotic consensus, i.e., the consensus of MASs could be realized only in infinite time.In order to solve the convergence rate problem of a system, scholars proposed the finite-time consensus,[14,15]which has features such as stronger robustness against uncertain influences and faster convergence rate compared with asymptotic consensus.In Ref.[14],for second-order MASs,the finite-time consensus was investigated.A finite-time distributed observer was used to calculate each agent’s mismatched disturbance.For finitetime output consensus and tracking consensus, two alternative control techniques have been developed.In Ref.[15],the finite-time consensus of MASs with input saturation and disturbances was investigated.A sliding mode control approach was introduced to deal with bounded disturbances.Different control protocols were designed for both leader-following and leaderless scenarios.
Noticeably, for the finite-time consensus, the convergence time is related to initial conditions of a system.However,the fixed-time consensus overcomes this constraint.For fixed-time consensus, a system could achieve consensus in a bounded time, and the settling time is independent of initial states.[16–20]In Refs.[17,18],the fixed-time consensus of nonlinear heterogeneous MASs was studied.In Ref.[19], for high-order non-global limited chain systems with unknown parameters and nonlinear uncertainties, the robust fixed-time tracking consensus was explored.An upgraded power integration technique was proposed to make the fixed-time consensus in MASs with uncertain parameters.
Compared with biological populations in nature, there are not only cooperative but also competitive relationships between species,for example,the relationship between pouncing and being pounced between sheep and wolves.Groups of the same species cooperate with each other,while the relationship between different species is competitive.Therefore, considering both the cooperative and competitive relationships in a system is very important for practical applications.[21–24]The consensus achieved under the cooperative-competitive system is called bipartite consensus,which is a unique case of group consensus.In Ref.[21], the group consensus of heterogeneous MASs in weakly connected topology with cooperativecompetitive relationships was investigated.In the design of control protocols, adaptive and hybrid pinning control methods are adopted.In Ref.[24], the cooperative-competitive group consensus for discrete-time MASs without the velocity of second-order agents was investigated by considering the input delay,communication delay,and packet loss.
In addition, in order to reduce the energy consumption of a system in control process, the event-triggered control method was proposed.[25–28]In Ref.[25], the problem of event-triggered consensus for nonlinear MASs was investigated,in which the continuous communication between agents in the system was not required.In Ref.[27], the eventtriggered consensus for the first-order MAS with input delay and uncertain disturbances was investigated.
ContributionsInspired by the above discussion, the fixed-time event-triggered group consensus for second-order MASs with disturbances is proposed in this work.The primary contributions of this work could be summarized as follows:
(i)Fixed-time group consensus of second-order MASs is investigated,which ensures that the settling time of the system is independent of initial conditions.
(ii)Unlike in traditional studies,cooperative-competitive relations between agents is taken into account.A signed structurally balanced communication topology is considered.
(iii)There is no Zeno behavior under the designed eventtriggered group consensus control protocol,and the system is resistant to interference.
OrganizationSome of the necessary concepts, lemmas,and problem formulation are given in Section 2.Sufficient conditions for the fixed-time group consensus and fixed-time event-triggered group consensus, and related proofs are presented in Section 3.Several numerical examples are presented to check the accuracy of the obtained results in Section 4.The conclusions and perspective on the future work are given in Section 5.
2.Preliminaries
2.1.Notations
Symbols and meanings used in this article are listed in Table 1.
The sign function is defined as follows:
Let softsign(x)=.Note that sign(x)≈softsign(σx)whenσ ≫1.
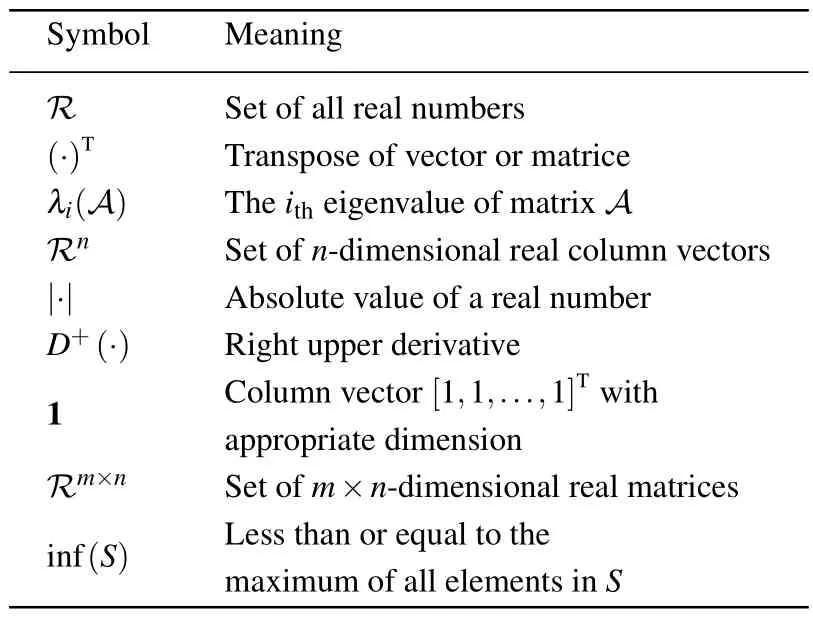
Table 1.Symbols and nomenclature.
2.2.Graph theory
2.3.Problem statement
Consider a second-order MAS consisting ofKagents with disturbances.The dynamics of each agent could be described as
wherexj(t),vj(t),uj(t)∈ℛdenote the position state, velocity state, and control input of the agentj, respectively,µ(xj(t),vj(t),t)∈ℛis the bounded disturbance.
2.4.Some definitions,lemmas and assumptions
Definition 1An undirected signed graphGis stated to connect if there exists a path between any two nodesνjand
νk.Gis said to be structurally balanced.If the vertex setVcould be divided into two partsV1andV2, then we have the following conditions:
whereV1∪V2=V,V1∩V2= /0.
Definition 2For MAS (1), if for any initial state, there
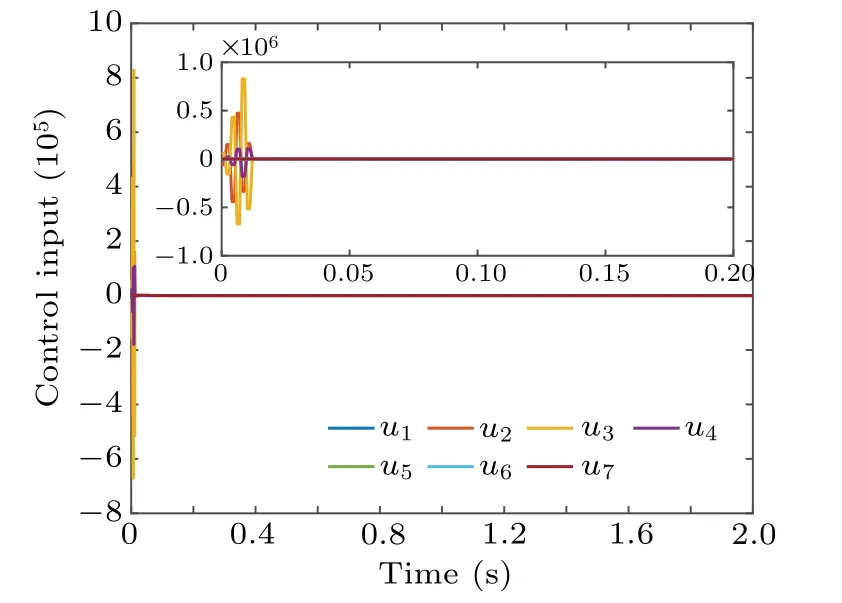
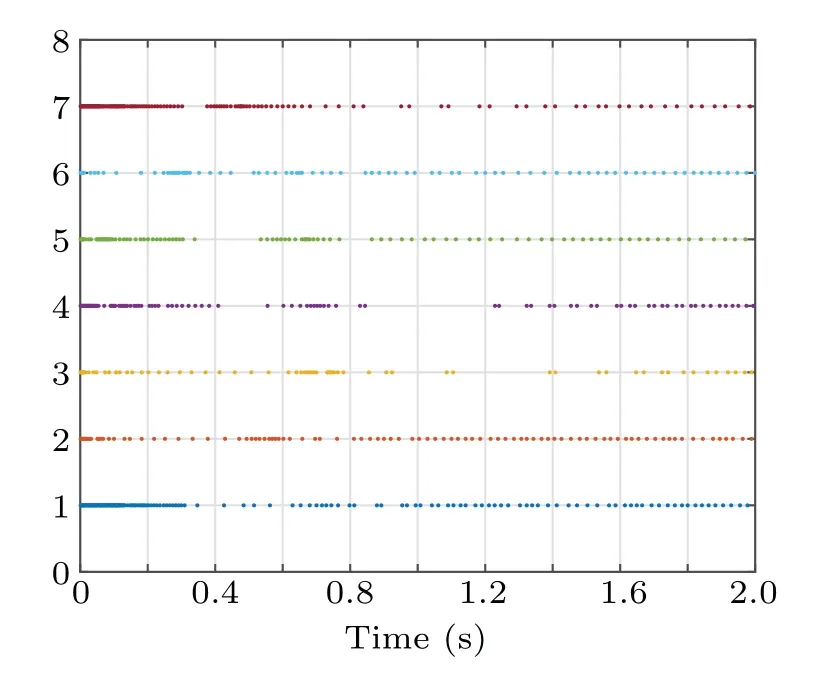
exists a settling time 0 Lemma 1[29]For a structurally balanced graph,there exists a transformationH=diag{h1,h2,...,hK}, such that all elements ofHAHare non-negative.Define a new Laplacian matrixℒgwhose elements are expressed as Then the eigenvalues ofℒare the same as those ofℒg. Lemma 2[30]For an unsigned undirected connected graphG, the Laplacian matrixℒsatisfies the following properties: (i)ℒis semi-positive definite and the eigenvalues ofℒcan be sequenced asλK>···>λ2>λ1=0. wherex=[x1,x2,...,xK]T. (iii)If 1Tx=0,thenxTℒx ≥λ2xTx. Lemma 3[31]Ifℓ1,ℓ2,...,ℓK ≥0,then there is Lemma 4[25]If there exists a continuous radially unbounded functionV:ℛn →ℛ+∪{0}satisfyingV(x) = 0 when and only whenx=0, and ˙V(x(t))≤−ρ1Vm(x(t))−ρ2Vn(x(t)),whereρ1,ρ2>0,m ∈(0,1),n ∈(1,∞),then the globally fixed-time stable could be derived and the settling timeTsatisfies Assumption 1The topology of system(1)is undirected signed,and structurally balanced. Assumption 2For the disturbanceµ(xj(t),vj(t),t),there is,j ∈ℐ, whereδis a nonnegative constant.That is,the disturbance is bounded. The problem of group consensus for second-order MASs with disturbances is analyzed in this section.Fixed-time control protocols and fixed-time event-triggered control protocols are designed,respectively. In the following,xj(t)−xk(t)andxj(t)+xk(t)represent the relationship between agentjand agentk,which are cooperative and competitive,respectively. Define whereSjandDjrepresent the set of neighbors that are in the same subgroup and different subgroup of agentj,respectively. For simplicity,rewriteχj(t),¯hj(t)as For MAS(1),the virtual velocity ˜vj(t)is introduced, Define the velocity errorzj(t)betweenvj(t)and ˜vj(t)as The control protocoluj(t)is designed to keep the actual velocity following the virtual velocity.That is, whereσ1,σ2,σ3,σ4,σ5>0 are control parameters,m ∈(0,1),n,r ∈(1,∞) are the ratio of positive odd numbers,d> 0,σ ≫1. Then,for derivative ofzj(t),there is Theorem 1Under the control protocol (4) withσ1,σ2,σ3,σ4,σ5>0,0 whereλ2is the minimum nonzero eigenvalue ofℒg,and ProofChoose the Lyapunov function as The derivative ofV1(t)along Eq.(5)is Due to∈(1,∞),according to Lemma 4,there exists a settling timeT1satisfying After the settling timeT1,the real velocityvj(t)could follow the virtual velocity ˜vj(t),thus the velocity errorzj(t)=0 fort>T1.From Eqs.(2)and(3),the real velocityvj(t)is Definex(t) = [x1(t),x2(t),...,xK(t)]T.Select the Lyapunov function as The derivative ofV2(t)along Eqs.(1)and(7)is From Lemma 2,one gets whereλ2andλKare the minimum nonzero eigenvalue and the maximum eigenvalue ofℒg,respectively. Combining Eq.(8)with Eq.(9)yields By now, whent ∈[0,T1], from Eq.(6), it follows that the errorszj(t) and ˜vj(t) are bounded.Combining Eqs.(1)and(3), it yields ˙xj(t)=zj(t)+˜vj(t), hence bothxandvare bounded.Whent ∈[T1,T2], from Eq.(8), MAS (1) could achieve fixed-time group consensus, and the settling timeTsatisfies Remark 1MAS(1)could achieve fixed-time group consensus under the control protocol (4).From Theorem 1, it could be shown that the settling timeTof the system (1) is independent of the initial conditions. The event-triggered control strategy is introduced on the basis of fixed-time group consensus.In comparison with general fixed-time group consensus methods, fixed-time eventtriggered control could better reduce the communication burden between agents.The study of an event-triggered technique is increasingly important when dealing with resource-limited microprocessors and bandwidth-limited networks. Therefore,design the control inputs for system(1)as Firstly,the measurement error is defined as Then,define the trigger function as whereι ∈(0,1).The performance of the system (1) could be adjusted by selecting the value ofι.Whenϕj(t)>0, the controller is triggered and the state of agentiis updated. The derivative ofzj(t)could be rewritten as Theorem 2Under the control protocol(11)withσ1,σ2,σ3,σ4,σ5>0,0 T ≤Tmax=T3max+T4max, whereλ2is the minimum nonzero eigenvalue ofℒg,and ProofThe Lyapunov function is chosen as The derivative ofV3(t)along Eq.(14)is Due to∈(1,∞),according to Lemma 4,there exists a settling timeT3satisfying After the settling timeT3,the real velocityvj(t)could follow the virtual velocity ˜vj(t),thus the velocity errorzj(t)=0 fort>T3.From Eqs.(2)and(3),the real velocity of agentj,j ∈ℐ,is Select the Lyapunov function as wherex(t)=[x1(t),x2(t),...,xK(t)]T. Along Eqs.(1) and (7), similar to the derivative ofV2(t)in Eq.(8),one can get the following derivative ofV4(t): Then, one can get that MAS (1) achieves fixed-time event-triggered control group consensus,and the settling timeTsatisfies Theorem 3For MAS(1),if the condition in Theorem 2 holds,then no Zeno behavior occurs under the event-triggered controller(11)with the event-triggered function(13). where Combined with the event-triggered conditionϕj(t)≥0, one obtains There is−≥>0.Hence, there is no Zeno behavior under the event-triggered controller (11) with the eventtriggered function(13). Remark 2If design control protocols based on sign function as usual,when the state error of agents in the system tends to 0, it will cause the control input to oscillate.Therefore,softsign function is introduced to replace the sign function in the control protocol,and it turns out that no Zeno behavior exists under the designed event-triggered controller(11)with the event-triggered function(13),which will be further illustrated in simulation examples. Suppose that the second-order MAS (1) contains seven agents, the communication topology is depicted in Fig.1,where the black solid lines represent a cooperative relationship between agents,andajk=1,the red solid lines represent a competitive relationship between agents,andajk=−1. Example 1The initial positions of agents are selected asx(0)=(1.3,−2.2,0.3,−3.5,−1.8,2.6,1.0)Tand the initial velocity asv(0)=(1,−3,5,−2,−6,2,−1)T. Under control protocol(4),setσ1=1.5,σ2=2.0,σ3=5.5,σ4=3.0,σ5=3.5,σ=20,m=5/9,n=23/9,r=7/5,d=1.6,δ=1.3,andµ(xj(t),vj(t),t)=0.8sin(xj(t))+0.5cos(vj(t)).Taking the transformation matrix to beH=diag{1,1,1,1,−1,−1,−1}, then it can be calculated that=1.382.Based on Theorem 1,one gets the settling timeT ≤1.21. Fig.1.The interaction topology G1. Fig.2.Trajectories of the position state. Fig.3.Trajectories of the velocity state. For MAS(1)overG1,Figs.2 and 3 give the position and velocity state trajectories of agents, which shows that agents 1, 2, 3, and 4 achieve to the same state, and agents 5, 6, and 7 tend to a different state.The system could achieve convergence within the settling timeTmax=2.5.Therefore, the desired goal of fixed-time group consensus is achieved. Example 2The initial positions of agents are selected asx(0)=(1,2.5,−3,1.5,−1,0.2,−0.6)Tand initial velocities are selected asv(0) = (2,−1.6,0.5,3.5,−3,2,−0.1)T.Under control protocol (11), setσ1=0.5,σ2=2.0,σ3=2.5,σ4=5.3,σ5=5.5,σ=10,m=5/7,n=3,r=9/7,d=0.8,δ=1.2,ι=0.3, and the disturbanceµ(xj(t),vj(t),t)=0.3sin(xj(t))+0.9cos(vj(t)).The transformation matrix isH=diag{1,1,1,1,−1,−1,−1}.It could be calculated that.Based on Theorem 2, one obtains the settling timeT ≤4.4. Fig.4.Trajectories of the position state. Fig.5.Trajectories of the velocity state. Fig.6.Control inputs of agents. Fig.7.The trigger instant of agents. For MAS (1) over theG1, the state trajectories of agents are given in Figs.4 and 5, the control inputs of agents are shown in Fig.6, and the trigger instant of agents in Fig.7.Under event-triggered control (11), the system could achieve convergence within the settling timeTmax=0.9, which illustrates that the desired goal of fixed-time event-triggered group consensus for second-order MAS(1)is achieved. The group consensus problem of second-order MASs with uncertain disturbances is explored in this paper.Separately, the fixed-time consensus with event-triggered control and without event-triggered control is investigated.Sufficient conditions for MASs to achieve group consensus are obtained.It is proved that no Zeno behavior is present under the designed event-triggered controller.The presented numerical simulations verify the potential correctness of the main results and the effectiveness of methods.The adaptive event-triggered group consensus for heterogeneous MASs will be studied in the future. Acknowledgements Project supported by the Graduate Student Research Innovation Project of Chongqing (Grant No.CYS22482),the National Natural Science Foundation of China (Grant No.61773082), the Science and Technology Research Program of Chongqing Municipal Education Commission(Grant No.KJZD-K202000601), and the Research Program of Chongqing Talent, China (Grant No.cstc2021ycjhbgzxm0044).3.Main results
3.1.Fixed-time group consensus
3.2.Fixed-time event-triggered consensus

4.Examples

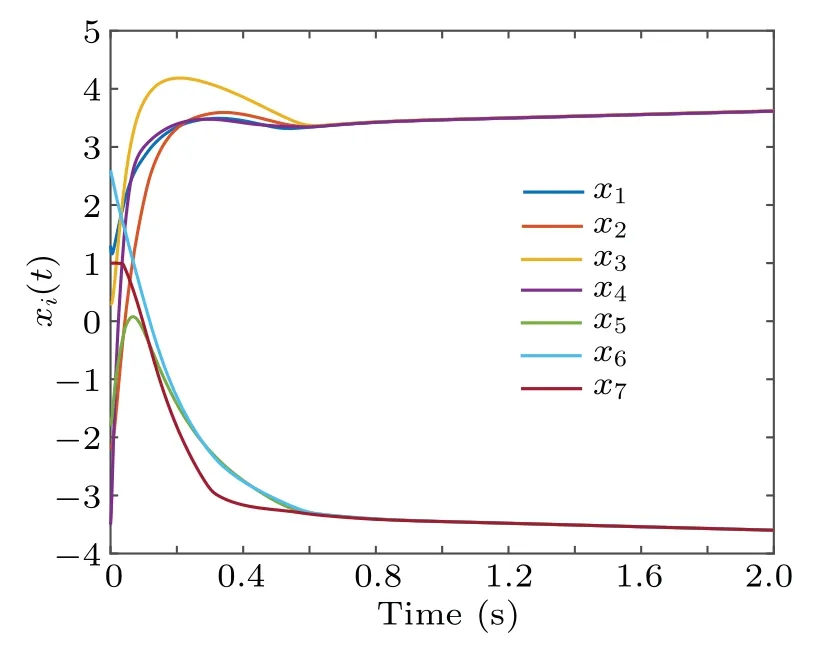
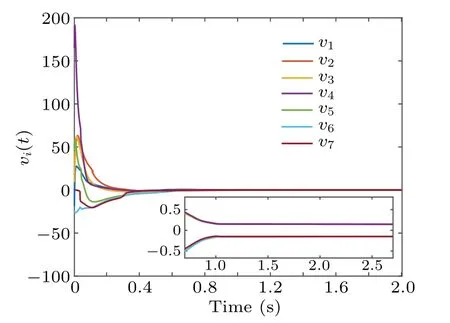
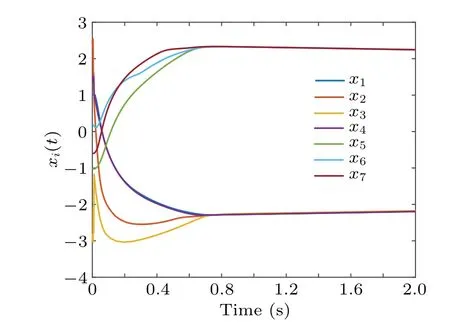

5.Conclusions
杂志排行
Chinese Physics B的其它文章
- First-principles calculations of high pressure and temperature properties of Fe7C3
- Monte Carlo calculation of the exposure of Chinese female astronauts to earth’s trapped radiation on board the Chinese Space Station
- Optimization of communication topology for persistent formation in case of communication faults
- Energy conversion materials for the space solar power station
- Stability of connected and automated vehicles platoon considering communications failures
- Lightweight and highly robust memristor-based hybrid neural networks for electroencephalogram signal processing
