一种改进的爬壁机器人全遍历路径规划

王 岩,李春书,张福龙

(河北工业大学机械工程学院,天津 300401)

1 引言

随着机器人技术的发展,对于一些高危、高空、有毒等工作环境比较恶劣或人工劳动强度比较大的场合,国内外研究者们开发了特种机器人系统去完成指定的作业任务。爬壁机器人在某些大型立面装置的检测、维修工作中得到了应用,如高层外墙、锅炉炉膛、船体壁面、石化储罐等装置的维护工作[1]。爬壁机器人在某些作业任务中需要遍历其工作区域,为了提高机器人的作业效率,全遍历路径规划需要考虑路径的覆盖率、重复率和遍历路径长度。

目前,国内外学者针对移动机器人全遍历路径规划的研究已有大量的研究成果[2-4],爬壁机器人在大型立面工作环境下采用的全遍历路径规划算法主要有生物激励神经网络算法、牛耕覆盖算法、內螺旋式遍历算法等[5-9]。陈克[10]针对桥梁检测爬壁机器人区域覆盖问题提出了一种改进生物激励神经网络全遍历算法,该算法结合了爬壁机器人能耗模型,实现了区域覆盖,但尚未考虑机器人陷入死区的情况。唐东林等[11]针对储罐检测爬壁机器人提出一种基于滚动窗口的优先级启发式路径规划算法,利用滚动窗口实现区域遍历,并且解决了机器人陷入死区的问题,但存在遍历路径过长和机器人转弯次数过多等问题。史国军[12]针对储油罐壁面爬壁机器人的漏磁探伤全遍历问题,提出了基于改进遗传算法与栅格法结合的完全遍历路径规划,减少了路径长度和运行时间,但该算法没有考虑含有U型障碍物的复杂环境。

针对立面维护作业的爬壁机器人,本文基于纵向迂回往复运动遍历方式,提出了优先级策略和逃离死区策略,实现了机器人对工作区域的全覆盖,并使其控制简单,易于设计和实现。

2 栅格地图构建

设爬壁机器人工作环境信息已知。根据机器人作业任务,首先将工作区域划分为若干个子区域,采用栅格法建立子区域栅格地图。栅格的大小是综合考虑机器人移动平台结构尺寸及其执行构件的运动特性来确定的,即机器人进入到某一栅格,可实现对此栅格的全覆盖作业。每一个栅格代表地图上的一个点。

设(xi,yi)表示第i个栅格的位置坐标,其中xi、yi分别表示栅格的横、纵坐标;同时对每一个栅格属性进行赋值,用“0、1、2”三种数值分别表示栅格的三种状态:障碍物栅格、未遍历栅格和已遍历栅格。通过对栅格属性进行赋值可判断机器人所处的环境状态;随着机器人的运动,已遍历栅格、未遍历栅格的数量也在变化和更新。

由于实际障碍物的形状通常与栅格形状不一致,因此建立的栅格地图中往往会存在一些无法与栅格单元边界完全相互重合的不规则障碍物,在进行栅格地图建模时就需要把这些障碍物做“膨胀”处理[13],变为有规则的栅格模型。如图1所示,其中黑色区域表示障碍物,白色区域表示需要遍历的区域。

图1 栅格地图环境建模

3 全遍历路径规划

3.1 改进的纵向迂回往复式遍历方案

对于轮式永磁吸附爬壁机器人,其在立面装置上竖直运动能耗小于水平运动[14],为了降低能耗选择纵向迂回往复运动方式进行路径遍历。在子区域中,为便于爬壁机器人的摘卸,设机器人的起始位置为栅格地图左下角,终点位置为栅格地图右下角。

机器人从起初位置出发,在纵向迂回往复式运动的基础上,设定其沿不同方向移动的优先级,将向左运动优先级设为最高,向上、向下运动优先级设为相同,向右运动优先级设为最低。当机器人运动至某一栅格位置,若左侧栅格为未遍历栅格,根据运动的优先级,机器人向左运动一个栅格;如果左侧栅格为障碍物栅格或已遍历栅格,再向上或向下方向检测是否为未遍历栅格,若不是未遍历栅格,则向右方向检测是否为未遍历栅格;以此确定机器人上下左右运动。

如图2所示为一子区域栅格地图,机器人从起始点出发,由于左侧为边界,根据纵向移动运动方式以及运动优先级策略,机器人将首先向其上方向检测,若为未遍历栅格,机器人将向上运动;若该方向没有障碍,则一直运动至边界,然后,向右运动一个栅格,再向下运动;当下方栅格为障碍物,左侧和向上的栅格为已遍历栅格,机器人将检测右边栅格,若为未遍历栅格,则向右运动一个栅格,再向下运动;依此类推。为使机器人的运动控制方便,其转向运动轨迹选择圆弧线。

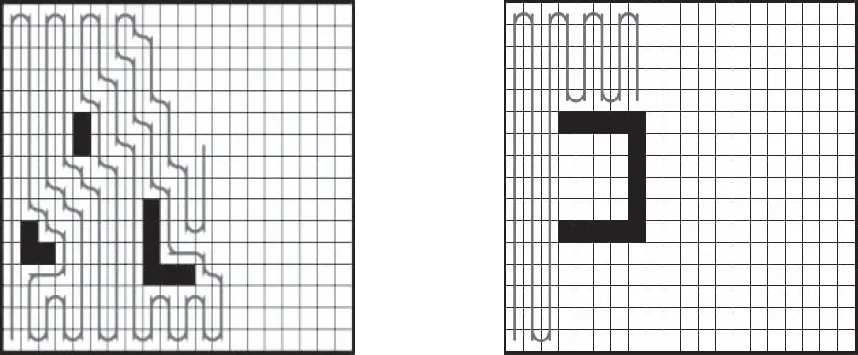
图2 纵向迂回遍历方案图3 U型障碍物开口向左

由于机器人向左运动设置为最高级别,从栅格地图上看遍历过程是从左向右沿着纵向迂回方式进行。当遇到类似U型障碍物开口向左时,会出现如图3所示的情况,无法对其内部遍历。为解决此问题,在此情况下将上述的优先策略切换为向右运动优先级设为最高,向上、向下运动优先级设为相同,向左运动优先级设为最低。这样,当机器人遍历这个U型内部区域后,再将优先策略切换回来。这也称为切换命令。切换命令将使机器人顺利遍历这种状态下的U型区域,如图4所示。其它状态下U型区域的遍历不需要执行切换命令,如图5所示。

3.2 逃离死区策略

当机器人运动到某一栅格位置,若其上下左右的栅格均为障碍物栅格或者已遍历栅格,且地图中仍存在未遍历栅格时,机器人即陷入死区位置。此时,为了提高遍历效率,机器人需快速寻找到一条尽可能短的路径来逃离死区。

针对此问题,本文提出了一种逃离死区策略。首先需要搜索一个预期目标点,然后,利用改进的灰狼路径规划算法计算出机器人移动至此目标点的路径,当机器人按照改进的灰狼路径规划算法计算出的路径移动至预期目标点时,则机器人逃离死区。

3.2.1 搜索预期目标点

当机器人陷入死区时,在利用改进的灰狼路径规划算法逃离死区之前,需要确定一个预期目标点,作为机器人逃离死区路径的终点。由于此目标点的选取影响机器人遍历重复率的高低,在充分考虑障碍物的基础上,选取实际距离机器人最近的点作为预期目标点,从而降低遍历重复率。

假设当机器人运行至P0(x0,y0)点时陷入死区,设定待选栅格位置为Pi(xi,yi),(i=1,…,m)m为待选目标点的总数。

1)当机器人与待选目标点位置连线不经过障碍物时,机器人与待选栅格之间的距离为di,如式(1)所示

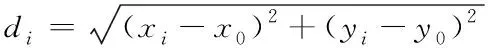
(1)

2)当机器人与待选目标点位置连线经过障碍物时,如图6所示,A、B、C、D为障碍物的四个顶点,此时机器人与待选栅格之间的距离为di为:

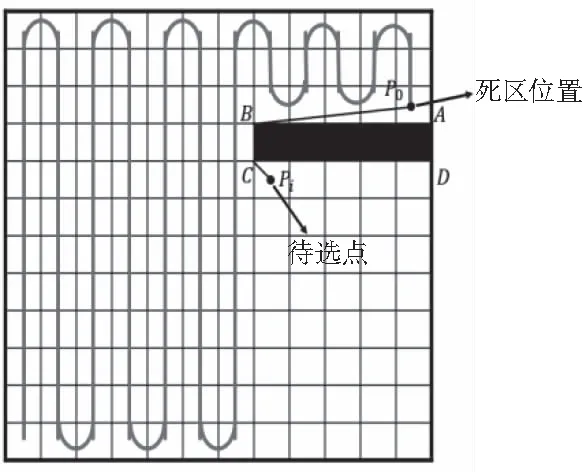
图6 存在障碍物时选取目标点

图7 改进的灰狼算法流程图

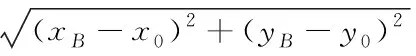
(2)

在求得所有待选点与机器人之间的距离di后,通过比较选取距离值最小的待选点为预期目标点。

3.2.2 改进的灰狼路径规划算法

当确定预期目标点后,机器人逃离死区的过程转化为点对点路径规划问题。本文采用改进的灰狼路径规划算法能够快速规划出最优逃离路径,较好地解决了此问题。

灰狼群体包括α、β、δ、ω四个群体,其α狼是最高领导者,拥有最高支配权,β和δ狼是支配权次之的两个群体,它们协助α狼管理狼群,并在狩猎时做出决定,ω狼是普通狼群。灰狼的狩猎过程描述如下:α狼带领整个群体搜索、跟踪、接近目标,β和δ狼在α狼的带领下围攻猎物,并带领ω狼狩猎目标,直到狩猎成功为止。传统的灰狼算法通过模拟整个灰狼群体的狩猎过程来实现目标的优化[16]。

灰狼确定目标位置后,包围目标的数学描述如下

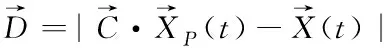
(3)

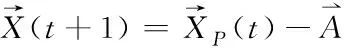
(4)

(5)

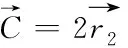
(6)

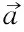
灰狼的狩猎行为数学描述如下

(7)

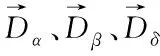
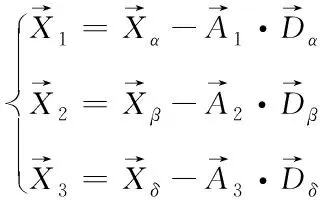
(8)

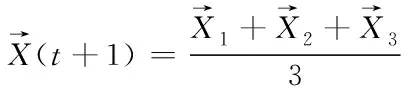
(9)

式(8)中分别定义了狼群中ω狼朝向α、β、δ狼方向前进的距离,式(9)定义了最终ω狼的位置。

(10)

其中,ω1、ω2和ω3取0.3,ω4取0.1。改进的灰狼算法流程图如下所示。

通过将改进的灰狼算法求解所得到的路径节点进行相连来确定规划的路径,设定灰狼算法路径规划的解为φ={(x0,y0),(x1,y1),…,(xn,yn),(xn+1,yn+1)},(x0,y0)为起点,(xn+1,yn+1)为终点,剩余其它点表示算法所需规划的坐标,n为改进灰狼算法求解得到的路径节点个数。如图8所示为利用改进的灰狼算法求解所得到的机器人路径规划。

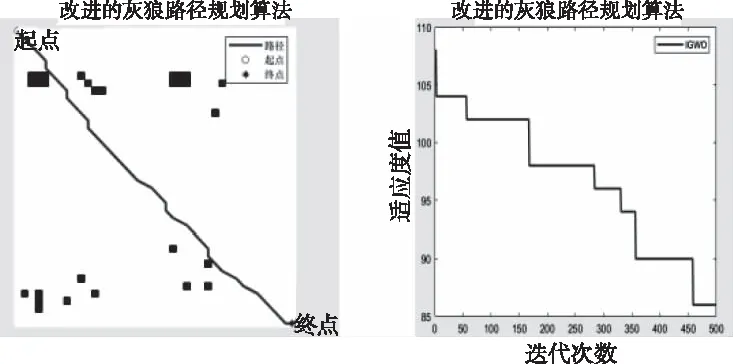
图8 改进的灰狼路径规划算法

如图9所示为机器人纵向迂回往复式遍历运动陷入死区位置及逃离死区位置的过程。在机器人逃离死区的过程中,只考虑障碍物栅格的影响,因此会增加遍历重复率,预期目标点的设计即为提高机器人遍历搜索的效率。

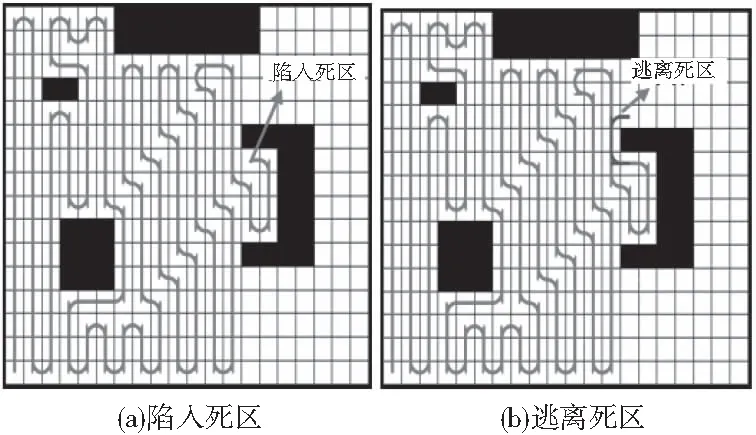
图9 逃离死区的过程

根据上述的改进全遍历路径规划方法,编制算法程序,其算法流程如图10所示。

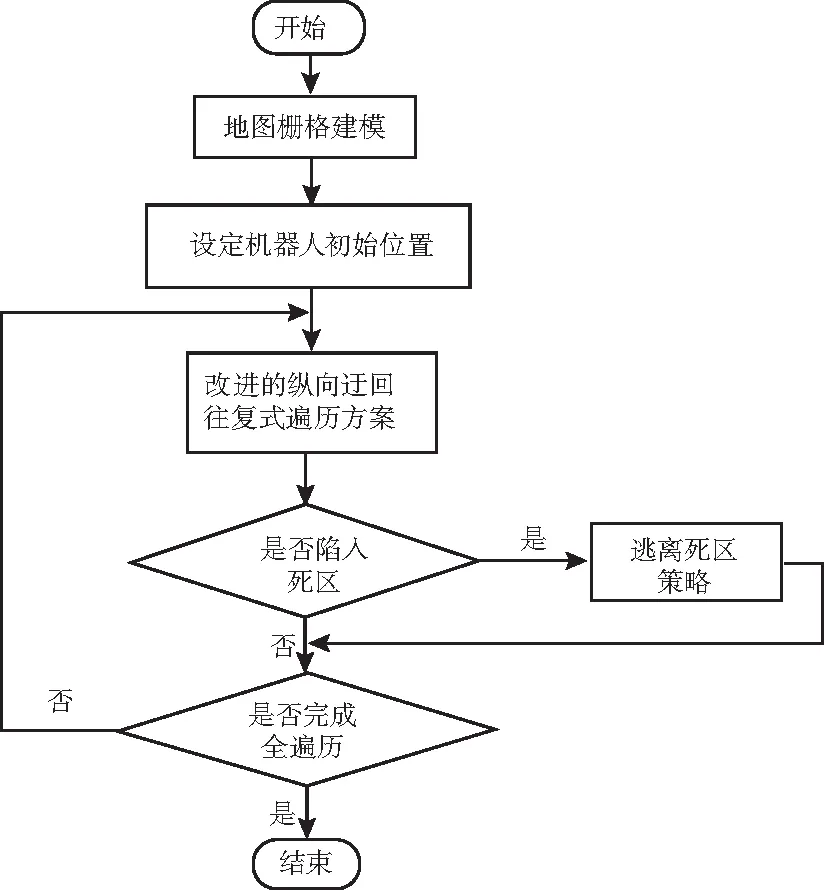
图10 全遍历路径规划算法流程图

4 仿真分析

为了验证本文提出算法的正确性,在相同的栅格地图上分别对文献[10]、文献[11]和本文算法进行了仿真,如图11所示。图中红色直线表示机器人遍历路径,蓝色直线表示重复遍历路径。

图11 不同算法仿真

通过图11的仿真结果得到不同算法下机器人全遍历的评价指标,如表1所示。通过分析可知,文献[10]算法不能完成全遍历工作,遍历覆盖率为98.91%;文献[11]算法遍历覆盖率为100%,重复率为5.82%;本文提出的算法遍历覆盖率为100%,且重复率和机器人转弯次数相对较低。

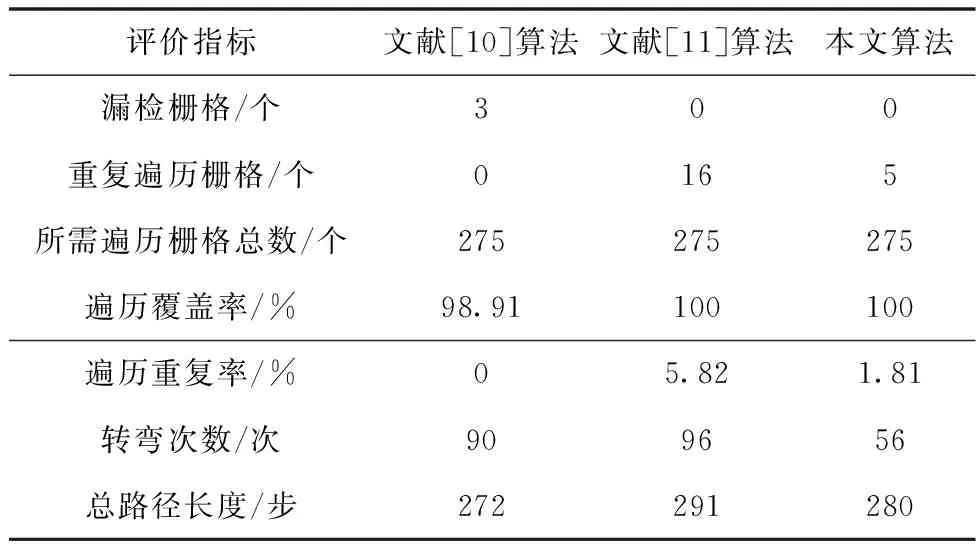
表1 不同算法全遍历评价

为了验证本文提出的算法在不同环境下的鲁棒性和有效性,分别在不同环境的栅格地图中进行仿真,遍历路径结果如图12所示。表2所示为不同环境下机器人全遍历的评价指标。

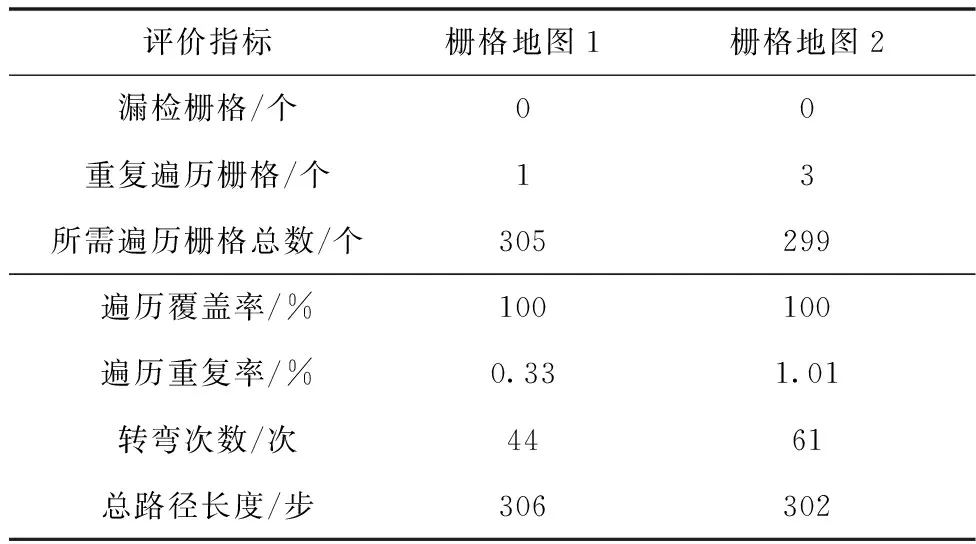
表2 本文算法全遍历评价

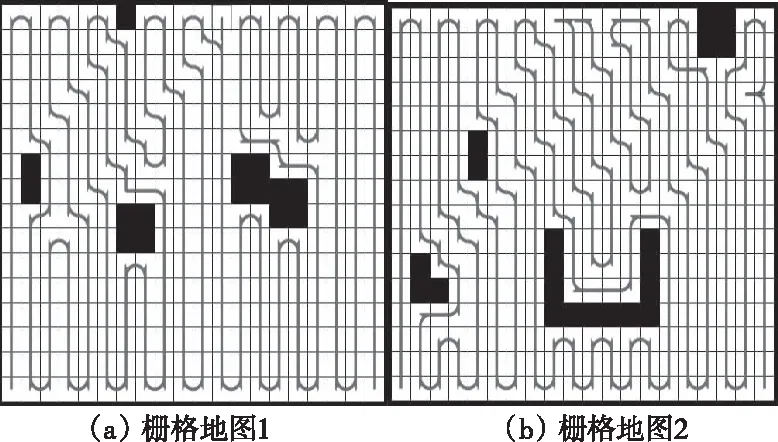
图12 不同地图仿真结果

仿真结果显示,当栅格地图中障碍物越多、形状越复杂,爬壁机器人的转弯次数就越多,相应的重复率较高、路径较长。本文所提出的改进全遍历路径规划算法遍历覆盖率高。

5 结论

本文提出了一种适用于立面维护作业的爬壁机器人全遍历路径规划,其将纵向迂回往复式运动与优先级策略相结合,在特定条件下启动切换命令,可实现机器人在有障碍物的环境中顺利遍历;当机器人陷入死区位置时,提出的逃离死区策略解决了机器人陷入死区的问题。在环境地图相同的条件下,将本文提出的全遍历规划方法与其它两种方法进行对比,仿真结果显示本文所提出的方法遍历覆盖率高、重复率较低。针对本文所提出的全遍历规划方法,在环境地图中障碍物的类型与布局不同的条件下进行仿真,结果显示其覆盖率高、重复率较低,是一种可行有效的全遍历路径规划。