线性离散时变系统的离散Walsh函数模型降阶
2023-09-04唐升国蒋耀林2王兆鸿
唐升国,蒋耀林2,,王兆鸿
(1. 新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046;2. 西安交通大学数学与统计学院,陕西 西安 710049)
1 引言
近年来,在众多工程应用领域,如电子系统、控制系统、微电子系统等,都涉及大型复杂动力系统的计算机仿真、优化与控制。这些系统一般用微分方程或差分方程描述。随着人们对系统精确度要求的不断提高,导致方程的维数也越来越大,有时甚至可以达到1011数量级。然而在实践中由于受到计算机有限内存空间和运算时间的限制,大规模系统的分析和仿真有时甚至是无法实现的。因此, 能否在有限计算资源下快速分析和仿真系统成为了制约工业前期设计的一个重要因素。模型降阶方法能够有效地解决这些问题[1]。此方法用一个低维系统去近似原始高维系统,并且可以保持原始系统的一些重要特性,如稳定性、可控性和可观性等。目前学者们已经提出了许多针对线性定常系统的模型降阶方法,如正交多项式模型降阶方法[2]、平衡截断模型降阶方法[3,4]和最优化模型降阶方法[5]等。
线性时变系统作为一类特殊的动力系统已被广泛研究[6,7],其中关于线性时变系统模型降阶的研究已获得大量关注。文献[8]利用TVP(time varying Padé)算法,将大规模线性时变系统变为具有相似输入输出传输特性的降阶系统。文献[9]提出了离散和连续时间线性时变系统的平衡截断模型降阶方法,同时还分析了误差界和保稳定性。文献[10]定义了线性时变对称系统的交叉Gram矩阵,并且基于可控、可观和交叉Gram矩阵之间的联系,研究了平衡截断模型降阶方法的保对称性。针对线性周期时变系统,文献[11]利用积分全等变换提出了基于投影的模型降阶算法,其中降阶系统能够匹配原始系统一定数目的矩。文献[12]借助离散Laguerre多项式,提出了线性离散周期时变系统基于Krylov子空间的模型降阶方法。经查阅文献发现,目前关于线性离散时变系统基于离散正交多项式的时域模型降阶方法的研究较少。因此本文研究线性离散时变系统基于离散Walsh函数的时域模型降阶。
针对线性离散时变系统,本文提出两种基于离散Walsh函数的模型降阶方法:①根据递推法得到线性离散时变系统状态方程的解,借助离散Walsh矩阵的性质得到离散Walsh函数系数矩阵,用所得系数矩阵构造正交投影矩阵,进而得到降阶系统。②把系统的各个变量用Walsh函数展开,从而获得对应的矩阵方程。通过求解矩阵方程得到状态变量的离散Walsh函数系数矩阵,再结合状态变量的非零初值得到正交投影矩阵并构造降阶系统。在单侧投影的理论框架下,理论分析表明这两种方法所得降阶系统分别能够匹配原始系统一定数目的展开系数。数值算例验证了本文所提方法的可行性和有效性。
2 预备知识
在本节中,将介绍离散Walsh函数的定义和性质。文献[13]给出了关于k的第i阶离散Walsh函数φi(k)。该函数被定义在N=2l个点上,其中l是非负整数;i和k是小于N的非负整数。令
(i)decimal=(il-1il-2…i0)binary
(k)decimal=(kl-1kl-2…k0)binary
(1)
则离散Walsh函数定义为
(2)
其中
g0(i)=il-1,g1(i)=il-1+il-2, …,gl(i)=i1+i0
例如,求N=24时的φ3(k),首先将十进制数3表示为四位的二进制数
(3)decimal=(0011)binary,
同时求出
g0(3)=i3=0,g1(3)=i3+i2=0,
g2(3)=i2+i1=1,g3(3)=i1+i0=2。
于是由式(1)和(2)可以得到
φ3(k)=(-1)[g0(3)k0+g1(3)k1+g2(3)k2+g3(3)k3]
即
φ3(k)=[1 1 1 1-1-1-1-1 1 1 1 1-1-1-1-1]。
离散多项式{φi(k),i=0, 1, …,N-1}构成一个完备集并满足正交性
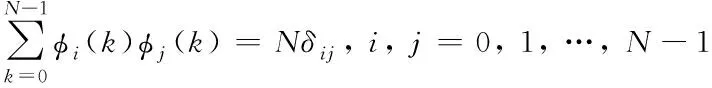
(3)
其中δij是克罗内克δ函数(Kronecker delta)。
给定任意有界离散序列x(k)∈Rn,x(k)可以被展成离散Walsh级数
(4)
其中
X=[x0x1…xN-1],xi∈Rn,
Φ(k)=[φ0(k)φ1(k) …φN-1(k)]T,
上标“T”表示向量或矩阵的转置。利用正交性(3),xi可以被计算出,即
离散Walsh矩阵W定义为[14]
W=[Φ(0)Φ(1) …Φ(N-1)]
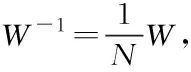
离散Walsh函数具有移位性质[15],即存在唯一的矩阵P∈RN×N使得
PΦ(0)=0,PΦ(k+1)=Φ(k)
(5)
成立,其中k=0, 1, …,N-2。事实上,式(5)还满足PW=WM,其中M被定义为
离散Walsh函数还具有乘法性质,它适用于适当维数的向量c,即
Φ(k)Φ(k)Tc=CΦ(k)
(6)
其中矩阵C是一个与向量c相关的矩阵[16]。进一步,当k=0, 1, …,N-1时,由式(6)可得[Φ(0)Φ(0)TcΦ(1)Φ(1)Tc…Φ(N-1)Φ(N-1)Tc]=CW,
即
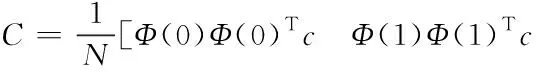
…Φ(N-1)Φ(N-1)Tc]W。
3 线性离散时变系统的离散Walsh函数模型降阶方法
在这一节,将提出两种基于离散Walsh函数的模型降阶方法。考虑如下线性离散时变系统
(7)
其中A(k)∈Rn×n,B(k)∈Rn×p,C(k)∈Rq×n是系数矩阵;x(k)∈Rn是n维状态变量,x(0)是初值;u(k)∈Rp和y(k)∈Rq分别是p维输入变量和q维输出变量。
本文的主要目的是构造正交投影矩阵V∈Rn×(≪n),然后在单侧投影框架下构造系统(7)的降阶系统
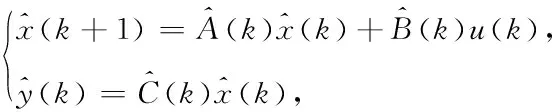
(8)
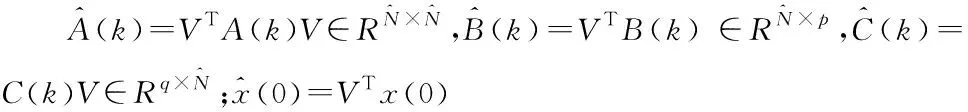
3.1 基于系统状态方程解的模型降阶方法
采用递推法,由系统(7)的第一个方程可知
x(k)=A(k-1)A(k-2)…A(0)x(0)+
×A(k-2)…A(j+1)B(j)u(j),
其中k≥2。根据式(4)可得
[x(0)x(1) …x(N-1)]
=X[Φ(0)Φ(1) …Φ(N-1)],
(9)
从而
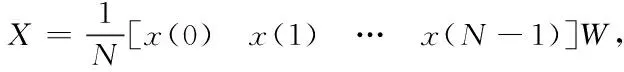
(10)
其中W是离散Walsh矩阵。
接下来,利用离散Walsh系数矩阵X构造正交投影矩阵V。需要执行Gram-Schmidt(GS)过程来构造V的列vi(i=0, 1, …, N-1)。此外,QR分解和改进的Gram-Schmidt(MGS)过程也可以用来构造正交投影矩阵V。上述降阶过程可以总结为如下算法。
算法1:基于系统状态方程解的模型降阶方法
输入变量:离散时变系统{A(k),B(k),C(k)}及初值x(0)
1)通过式(10)计算出离散Walsh系数矩阵X;
2)构造投影矩阵V∈Rn×N,它满足
colspan{X}⊆colspan{V},VTV=IN;
注 1:在式(10)中, 由于离散Walsh矩阵W∈RN×N非奇异,所以有X∈Rn×N(N≪n)和V∈Rn×N(N≪n), 因此降阶系统的阶数为=N=2l。
注 2:在式(10)中,如果x(0)=0或X不是列满秩的,则可以选取X的列向量中最大线性无关组来构造正交投影矩阵V∈Rn×N1(N1 事实上,在3.1节中已经提出了具有系统非零初值的模型降阶方法。在这一节将研究另外一种具有系统非零初值的模型降阶方法。 根据离散Walsh级数的性质,x(k+1)∈Rn可以被展开为 于是有 [x(1)x(2) …x(N)] (11) 又由于 [x(0)x(1) …x(N-1)] =[x(1)x(2) …x(N)]M+[x(0) 0 … 0], 所以将式(9)和(11)带入上式并化简可得 (12) 其中 X0=x(0)Φ(0)T=[x(0)x(0) …x(0)]∈Rn×N。 根据离散Walsh级数的性质,系统(7)中的各个变量还可以表示为 x(k)=XΦ(k)=(Φ(k)T⊗In)vec(X), u(k)=UΦ(k)=(Φ(k)T⊗Ip)vec(U),U∈Rp×N, 其中⊗表示Kronecker积,vec(·)表示矩阵的按列拉直算子。用类似得到式(10)的方法, 还可以得到 于是, 将上述各式代入系统(7)的第一个方程中可得 接着应用性质(6)可得 由于上述各式对k=0,1,…,N-1都成立,所以利用离散Walsh矩阵W,有 从而 (13) 成立。结合式(12)和(13)可得 (14) 算法2:具有系统非零初值的模型降阶方法 输入变量:离散时变系统{A(k),B(k),C(k)}及初值x(0) 2)构造正交投影矩阵V∈Rn×,它满足关系 相似地,原始系统(7)的输出变量y(k)也可以表示为 于是,由算法1得到的降阶系统(8)满足如下定理。 证明:在算法1中,由于x(k)的离散Walsh函数系数矩阵为 (15) 对系统(15)的第一个方程左乘矩阵VT,有 (16) 相似地,由算法2得到的降阶系统(8)也满足如下定理。 定理 2:若V是由算法2得到,则当k=0, 1, …,-1时,成立。进一步,有X=V和Y=。 所以x(k)⊆colspan{X}⊆colspan{V}成立,k=0, 1, …,-1。因为接下来的证明过程与定理1的证明过程类似,所以此处省略。证毕。 在这一节中,将应用一个数值例子验证算法1和算法2的可行性和有效性。 考虑如下偏微分方程[12] (17) 用500个网格,对偏微分方程(17)进行有限差分离散,根据初值条件可以得到499阶的连续时变系统。令p=+∞和时间步长Δt=0.5,利用向后欧拉法可以得到一个n=499的线性离散时变系统。令ξ(t)=1+t,ξ1(t)=t+tsin(t),ξ2(t)=1,z(0,0.002)=0.1, …,z(0,0.6)=0.1,z(0,0.602)=0,…,z(0,0.998)=0。假设算法1的降阶阶数为=8,算法2的降阶阶数为=9。当u(t)=(-1)2te0.01t时,图1描述了原始系统和降阶系统的输出;图2给出了原始系统和降阶系统输出的绝对误差。从图1可以看出由算法1和算法2得到的降阶系统的输出能够很好地逼近原始系统的输出。在图2中,可以观察到由算法1得到的降阶系统的输出能够匹配原始系统的前8个输出y(k),然而由算法2得到的降阶系统的输出能够匹配原始系统的前9个输出y(k)。因此,由算法1和算法2得到的降阶系统分别满足定理1和定理2的结论。 图1 原始系统和降阶系统的输出 图2 绝对误差 本文利用离散Walsh函数研究了线性离散时变系统的时域模型降阶,并提出了两种模型降阶方法:①采用递推法,得到线性离散时变系统的状态变量x(k)(k=0, 1, …,-1),并结合离散Walsh函数的性质得到状态变量x(k)的离散Walsh函数系数矩阵,将得到的系数矩阵构造正交投影矩阵,进而得到降阶系统。②将线性离散时变系统在离散Walsh函数构成的空间中展成矩阵方程,通过求解矩阵方程得到状态变量的离散Walsh函数系数矩阵。利用所得系数矩阵和非零初值x(0)构造正交投影矩阵并得到降阶系统。理论分析表明上述两种方法得到的降阶系统分别能够匹配原始系统一定数目的展开系数。数值算例验证了本文所提方法的可行性和有效性。3.2 具有系统非零初值的模型降阶方法
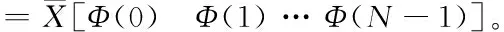
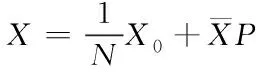


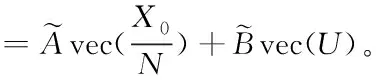
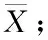
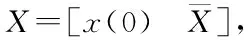
3.3 系数匹配
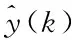
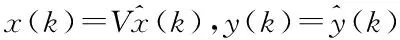
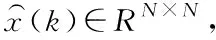
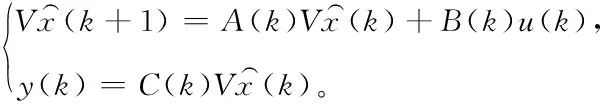


4 数值实验
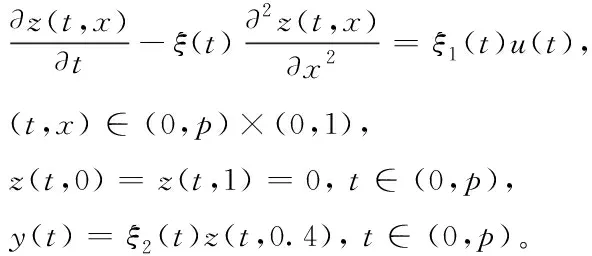
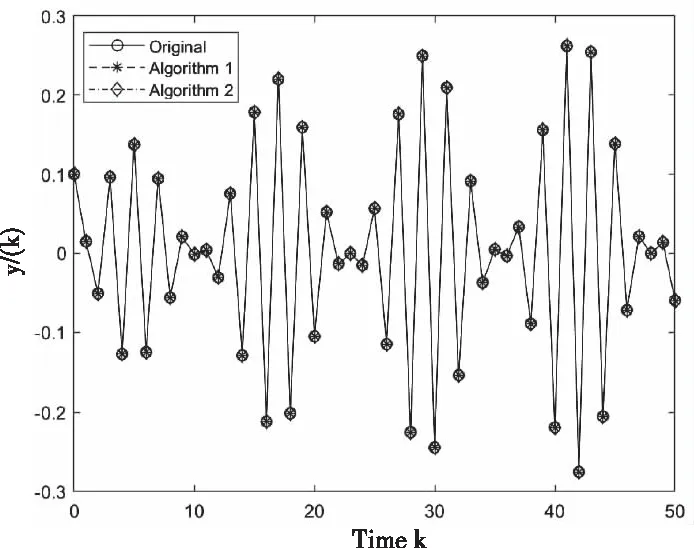
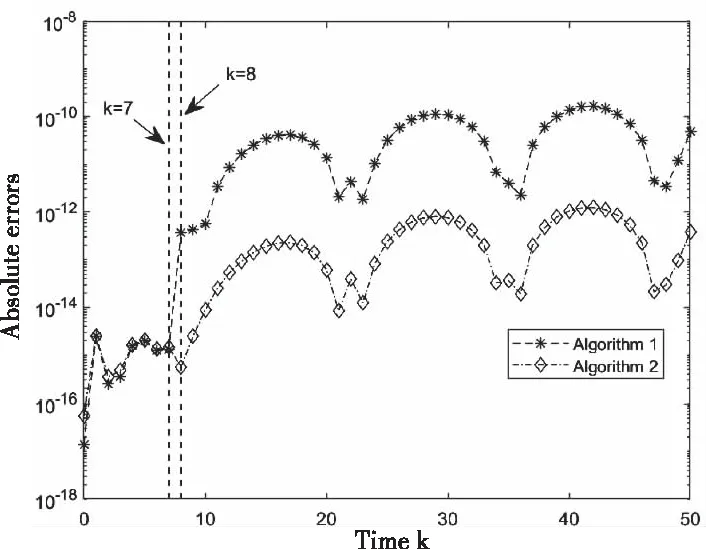
5 结论
