基于遗传算法的工业炸药仓储优化研究与仿真
2023-09-04徐钒诚谌海云杨帅东
徐钒诚,谌海云,杨帅东,李 洋
(西南石油大学,四川 成都 610500)
1 引言
随着我国基础建设的大力开展,民爆行业伴随着这种需求得到极大发展,工业炸药作为民爆行业中的支柱产业,其需求量也得到极大上升[1],但由于工业炸药的特殊性,一直受到监管部门的严格管控,尤其在工业炸药的仓储管理中,更是有着极其严格的要求。这也导致工业炸药仓储目前仍采用人工管理的方式,存在管理效率低下,货位摆放混乱等问题。如何实现工业炸药仓库群以及炸药高效的货位动态分配及优化问题已成为一个迫切需要解决的难题。文献[2]中要求民爆生产企业以现代化仓储管理技术为依托,提高仓库作业效率及仓库空间使用率。文献[3]中鼓励企业建立工业炸药产品仓储的信息化、智能化和可视化监管体系。因此对工业炸药仓储过程进行优化,对于降低工业炸药仓储运行成本、提高仓库群的整体空间利用率具有非常重要的现实应用意义。
工业炸药作为一种特殊的物品,其仓储过程由于行业的局限性,目前关于工业炸药仓储过程的研究很少。Anonymous[4]等首次在文章中提出爆炸物安全存储要求和标准,成为许多国家工业炸药管理标准。李宇[5]等将RFID(Radio Frequency Identification)技术应用在雷管产品的安全管理,算是国内首次将电子产品用于危爆物品中。孟广雄[6]对于混装炸药的智能化生产与管理进行了探究,在文中提出了炸药产品管理方式的智能化改造和升级的新构思。付华伟[6]等第一次完整的提出工业炸药仓库货位优化模型,但仅仅研究的是将多种类炸药产品放置在一个仓库下的优化问题。之后由于行业特殊性和局限性,工业炸药仓储过程的研究处于停滞不前的状态。
工业炸药仓储是一个复杂的货物存取过程,属于组合优化问题,亦是一个典型的NP难题[6]:炸药产品不同规格的产品的包装质量是相同的;不同时间内市场对于炸药的需求量存在较大的差异,如何保证实时调整炸药存放位置以及同类货物如何做到集中存放;工业炸药产品有着时效性的问题,如何保证产品的先入先出等。针对上述问题,本文首先在分析工业炸药仓储过程特点的基础上,对工业炸药仓储过程进行数学建模;然后基于构建的数学模型,使用遗传算法进行求解,针对遗传算法求解过程中出现的早熟收敛、进度不足的问题,提出一种基于信息熵及改进的自适应算子的混合遗传算法,并将本文算法与传统遗传算法进行对比,验证算法的有效性;最后使用新算法对模型求解,实现炸药仓储的操作优化。
2 问题描述
2.1 问题提出
工业炸药产品在生产到使用的过程中,都需要存放至指定的仓库中。由于其产品的特殊性,在炸药产品进出库时,同时需要考虑多种因素:
1)产品摆放的安全性问题。工业炸药产品仓库内摆放的安全性监管部门关注的重点,文献[8]中对于炸药产品在仓库中的摆放位置有着严格的要求,不合理的摆放布局方式将会导致仓库库容的下降的同时降低炸药存放的安全系数。具体要求如下表1所示。

表1 安全存放要求表
2)炸药产品存放的安全性问题。工业炸药因为类别的不同,其危险性和易爆性也不同。这就要求在进行库区分配时具有高爆性的炸药不能同时存放在一个仓库内,此外在同类产品在安全系数越低的个体也应距离出入口更近。
3)产品存储的时效性问题。工业炸药产品是根据国家的规定及需求按量生产,且产品会随着存放时间的增加降低其安全性,进而增加安全隐患,因此工业炸药产品应该严格遵循先入先出原则。
4)产品出入库的不确定性问题。由于工业炸药出入库作业的时间、数量等完全由市场决定,充满不确定性,存在几天都不进出库或一天进出几次库的情况且每次出库产品的种类不尽相同的情况。
5)产品进出库的不同类问题。工业炸药产品在实际使用中存在混装的情况,因此在单次出入库时可能会存在几类炸药产品同时出入库的情形。
6)仓库群分布的地理性问题。工业炸药仓库群为安全性考虑通常只有一个出入口,通常情况下工人们对于仓库群的管理仅简单的根据产品出入库的数量将炸药产品堆放至离出入口最近的仓库。这也直接导致离出入口最近的仓库经常满仓且堆放产品种类较多,而距出入口较远的仓库经常空库,进而致使仓库群的整体使用效率低下。
2.2 模型假设
本文根据某工业炸药公司仓储现状将模型简化,描述如下:仓库库区中共有5座结构、容量相同的独立仓库,每个仓库内含有两个库区且均可存放任意种类的工业炸药产品,将距离出入口最近的仓库标记为1号仓库,对应库区为1,2号库区。图一为某工业炸药仓库群及库区示意图。
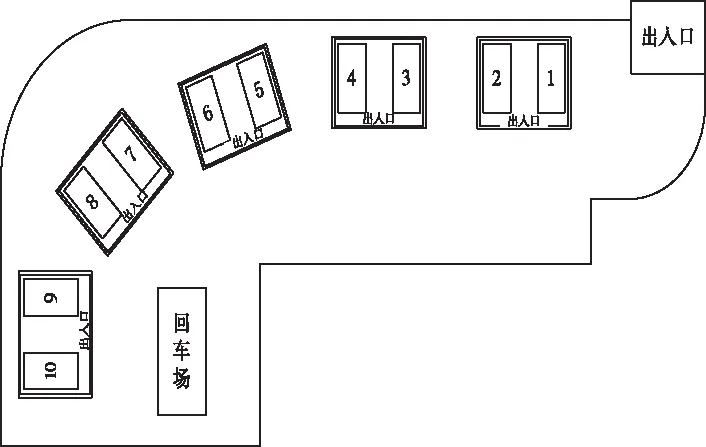
图1 仓库群及库区示意图
仓库库区中,炸药产品以堆垛的形式进行存放,以仓库出入口位置为坐标原点,将距离仓库出入口最近的一排记为第1排,以出入口对应为y轴,将仓库分为两个库区,其靠近出入口的为第1列。那么该库区内的货位坐标可记为(x,y),(x=1,2,…,P;y=1,2…,Q),仓库内具体摆放布局如下图2所示。
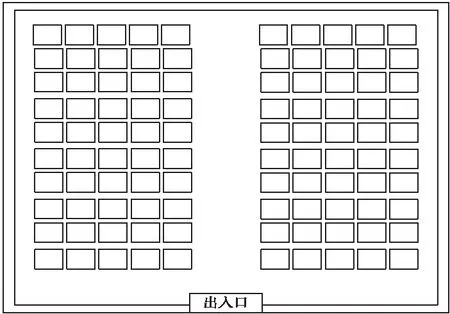
图2 仓库摆放布局图

图3 本文算法流程框图

根据以上描述,将本文进行仓储优化的假设总结如下:
1)工业炸药存放的种类已知,且摆放的堆垛长宽以及形状都相同;
2)每种工业炸药的周转率、质量和初始安全系数已知;
3)每个仓库最多可存放两类货物,每个库区只能存储一类产品;
4)仓库及仓库群出入均采用单端出入库的方式。
5)假定同类别的炸药其初始安全系数及变化幅度均相等,设定sk≤β时,该类炸药为不易爆产品,sk>β时为易爆产品。同时对于单一产品个体可能会随着被保存时间的增加变为易爆产品。
3 工业炸药仓储优化数学模型
根据以上问题描述及模型假设。本文将以提高仓库群整体空间利用率和产品进出仓库效率为优化目的;针对单一仓库内货位优化,以就近存放原则、货物相关性原则和出入库效率最高作为具体优化的目标,建立货位优化的多目标数学模型。
3.1 仓库群动态分配模型
针对仓库群的动态分配问题,国内外学者做了大量研究。张永强[9]等人使用SLP和SHA对林产品仓储布局进行优化,提出根据订单动态分配仓库功能区域,并对仓库功能区域面积和作业区域进行优化;赵雪峰[10]等人采用Heskett给出的立方体索引号(Cube-per-Order,COI)规则实现仓库内的货位动态分配;曹现刚[11]等人在自动化立体仓库优化研究中使用专家打分法实现对仓库群的动态分配。综合以上文献,本文针对仓库群动态分配问题,建立仓库群动态分配模型如下:
1)库区分配权重函数

(1)
式中:fk为某种货物在某一时间段内的出入库频率,Ck为某种货物仓库存储所需的总量,n为炸药产品的类别数,模型(1)中M的值代表货物在仓库群分配中所占权重,M越大,产品存放仓库距离仓库群出口越近。
2)每个库区内存放工业的炸药类型由以下模型决定
D[i][j]=D[rank(Mi)] [Si] *D[rank(Mi+1)] [Si+1]T
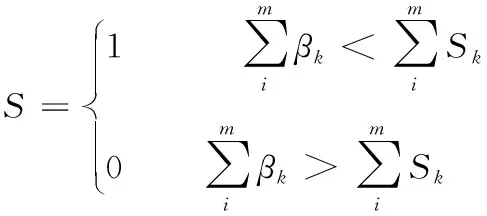
(2)
其中D[i][j]为存放权值矩阵,D[i][j]为1时,表明相邻库区存放的炸药产品不全为高危险性炸药产品。i代表所存放的库区号,j表示存放的货物是否为高危险性产品,rank(M)为产品库区动态分配权重值,S=0时代表该类产品为高爆性炸药产品。

(3)
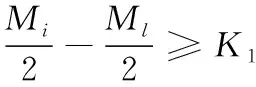
(4)
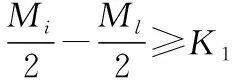

Lk=rand(rank(Mi,Mj)*D[i][j])
(5)
模型(5)表示当两种类型的产品出入库频率相近时,其库区的选择首先根据式(2)及M的值确定存放的仓库范围,再在此范围内随机选择放入的产品类型。
3.2 仓库内货位动态分配模型
根据问题描述,考虑以产品先入先出、同一库区存放同类货物原则、就近存放原则为主要,以保存时间和出入库频率作为次要考虑因素,建立如下货位分配模型:
1) 设仓库内搬运小车在水平和竖直方向运动速度分别为Vx以及Vy且恒定,堆垛的长度记为a,宽度为b,judge=0or1,其中judge=0代表货位未存放货物、judge=1为货位已存放货物,此时改货位不可存放,就近存放可由函数F1表示
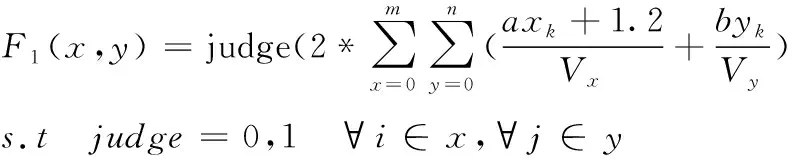
(6)
2)以单位时间内单一库区出入库频率及保存时间建立函数F2,统计单位时间内某一类炸药出入库频率记为fk,炸药的保存时间记为Pk,故
F2=fk*Pk
(7)
s.tXk=0,1 ∀k∈(x,y)
(8)
模型中函数(7)为存储时间矩阵,X=0时代表此时处于入库状态,产品保存时间都统一为1,若X=1则为出库状态,随着保存时间的增加其权值系数会呈指数增长,以保证先入先出。
3)考虑到同批次的货物进出库的货物可能不尽相同,甚至会存在多种类别的产品同时进出库的情形,因此同类产品应严格存放在同一库区且存放位置相邻,建立炸药存放相关性函数为
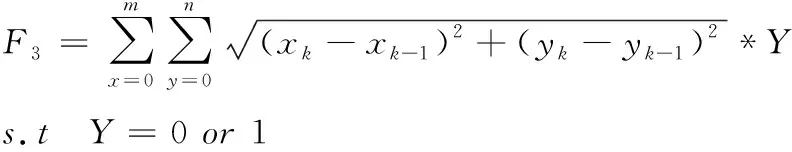
(9)
其中为xk与xk-1为同类货物是Y=1,反之则为0。
根据以上模型构建,仓库内货位动态分配模型实际是一个多目标组合优化问题,并可拆分为出库和入库两种状态,且在出入库时对应函数所求值的冲突较小,因此构建总的货位动态分配函数F如式(9)(10)所示,其中X代表出入库状态,X=0时为入库状态。

(10)
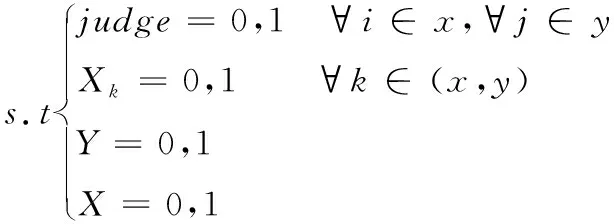
(11)
经过以上处理,炸药存放变为了一个货位只能存放一个堆垛,一个区内只能存放同一类货物,货位分配分为出库和入库两种状态,即模型整体变为了0-1指派问题,降低了模型求解难度。
4 改进遗传算法求解
4.1 标准遗传算法设计
遗传算法(GA)作为一种经典的普适性随机优化算法,于1975年由Holland教授首次提出,它是一种模拟自然生物的遗传进化模型[12],具有搜索速度快、随机性强、过程简单等优点[7],
1)编码:将存储坐标与出(入)库选择点对应关系作为解,因此采用整数编码,个体编码由存放的坐标点构成。因实际操作中单次出入库时共需操作的堆垛数在10个左右,共分两次出入库,故本文中单条染色体的长度设为5,如某一类炸药产品的优化求解坐标分别是(02,05)、(04,05)、(05,07)、(01,03)、(08,02),则这5个货位坐标作为基因组成一个具体的染色体可表示为“02050405050701030802”;
2)初始种群得到产生:初始的种群在解空间中用随机的方法产生;
3)适应度函数设计:遗传算法中的适应度函数用来评定群体中各个个体对于环境的适应性,有助与帮助找到最优解。由本文所提模型总的目标函数可知为求解全局最小值问题,本文中适应度函数如下所示
minf(x,y)=F(x,y)
(12)
4)选择:锦标赛选择算子作为比较流行的选择策略,相比于轮盘赌的选择方法,其选择出的个体一定是当代种群中最优个体。使用锦标赛选择后的个体可以直接进行交叉操作。
5)交叉。变异算子
交叉和变异分别是GA产生新个体的主要方法和产生新个体的次要途径[13]。其中变异算子直接影响着算法的局部搜索能力和种群的多样性。交叉方式按照单点交叉进行交叉操作;变异方式采用随机选择变异位的方式进行变异操作。变异的概率由自适应遗传算法(AGA)计算,其计算公式如下
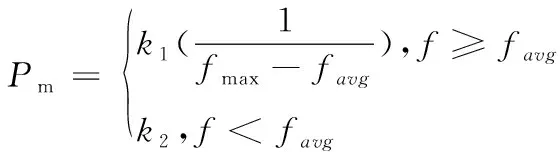
(13)
其中fmax、favg为当前种群的最大适应度值和平均适应度值,k1,k2为人为定义的一个参数值。由式(12)可以看出该方法定义下的自适应函数其实在整个种群基础上进行的计算,无法对每个个体概率进行精准操作。
4.2 改进后的遗传算法
由于传统遗传算法的局部寻优能力不足,随着迭代的进行,随着种群质量的上升,种群适应度的下降,反而不能获得足够的优秀个体,常常几个坐标收敛于同一个坐标下,且仍存在收敛速度慢,精度不足等问题。因此本文根据信息熵概念,提出使用信息熵作为种群多样性评价标准,以解决种群多样性过低导致的最优解集中问题。并在自适应遗传算法(AGA)的基础上,提出改进后的自适应算子。
4.2.1 信息熵值
信息熵是信息论中的一个重要概念,由香农发表的著名论文《A Mathematical Theory of Communication》首次提出,奠定了信息论的理论基础。在这一理论中,熵值定量描述了随机变量的不确定程度[14],即可以将信息熵用于衡量信息或者选择中的不确定性程度。
确定的信息熵通常代表信息源X可能发布的不同特征的信息在信息源概率空间的统计平均值[15],即熵值越高代表信息源的不确定性程度越高。其计算公式如下:

(14)
其中P(X)为不确定值在整个信息源中的概率。综上,本文尝试将信息熵作为种群多样性的度量标准。即,种群多样性越复杂,对应的熵值越高,反之亦然。
4.2.2 自适应变异算子
为克服自适应遗传算法(AGA)中存在的无法有效得到全局最优点的问题[16],本文在AGA的基础上,提出改进后的自适应变异算子。
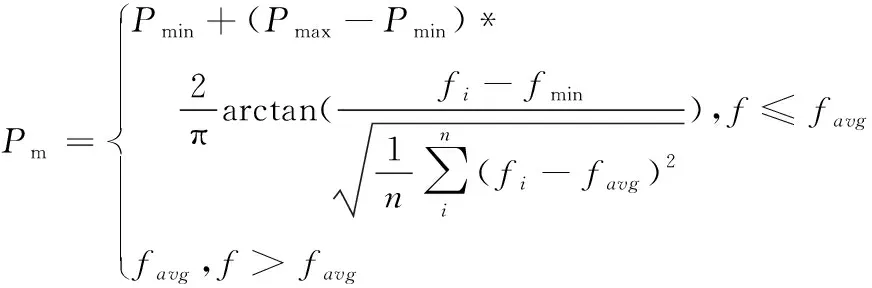
(15)
Pmax,Pmin为最大、最小变异概率;fmax为个体的最大适应度值;favg为种群适应度均值;fmin为个体的最小适应度值;fi为变异个体适应度值。由式(15)可知,适应度值越小的个体(即本应在自然选择时被淘汰的个体),对应变异概率越大,进而增大了被选择的概率,从而提升种群多样性。
4.3 改进后的遗传算法步骤
综上所述,确定基于信息熵及改进后的自适应变异算子的遗传算法流程如下:
5 实验对比及结果分析
5.1 算法对比
为验证改进后的算法的有效性,本节将使用改进的算法与标准遗传算法在测试函数—比尔函数 (Beale Function)下进行比较;比尔函数是取值范围x,y∈[-4.5,4.5]上的一个多峰函数,其函数图像共有四个峰顶极值、四个峰谷极值,在[3,0.5]时取得全局最优值0。故使用比尔函数测试算法时,能够有效检验算法的寻优能力。
同时为验证信息熵以及自适应变异算子在算法中的作用,实验使用标准GA算法、仅自适应变异算子、仅信息熵、以及本文混合算法下的结果进行比较。
首先设定初始种群个体数nind=50;最大遗传代数maxgen=100代;初始交叉概率为Pc=0.8;初始变异概率Pm=0.1,变异概率取值范围为Pm∈[0.05,0.1]和Pm∈[0.075,0.15],Pm的取值范围随种群信息熵值自适应选择,信息熵阈值S0=[3.5,6],具体的值随着nind的值改变而改变;实验结果如下所示。
根据图4,在比尔函数下,标准遗传算法比本文算法多运算了30代并在40代附近收敛;同时在仅信息熵和仅变异算子条件下,算法虽未收敛至全局最优,但其中期陷入局部收敛的时间大幅缩小。同时由图5可以看出信息熵值随着种群的迭代都呈不断下降的趋势。在使用信息熵作为种群多样性的度量标准的条件下,种群信息熵值均大于标准遗传算法和仅使用变异算子,即信息熵能够实现对种群多样性的动态调整;此外,从第7次迭代开始,标准遗传算法的种群多样性大于仅变异算子的作用下,但在第8代后种群多样性得到明显提升,故自适应的变异算子起到了其本身的作用。
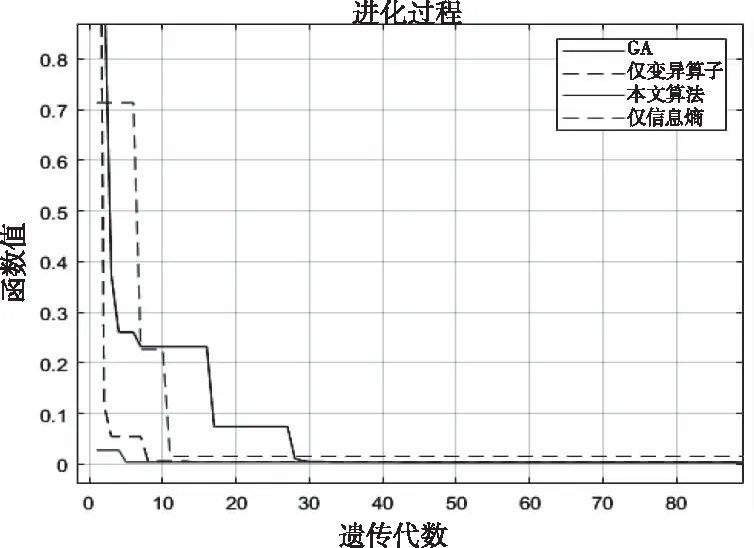
图4 nind=50时,算法迭代对比图
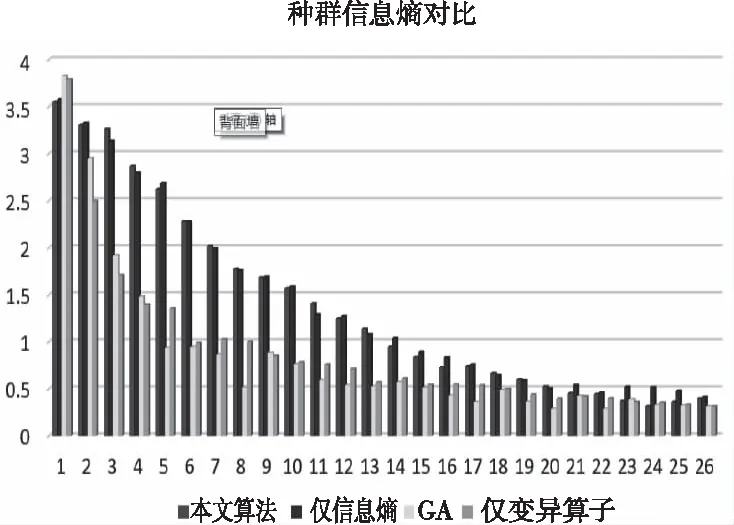
图5 nind=50时,种群信息熵值比较
为避免偶然因素导致算法比较错误,本文在上文的基础上,仅改变初始种群个体数nind的大小,重复进行实验,特别注意,为保证种群信息熵值比较效果,实验时统一取25代迭代并求其平均做统计;其统计数据如下表2所示。
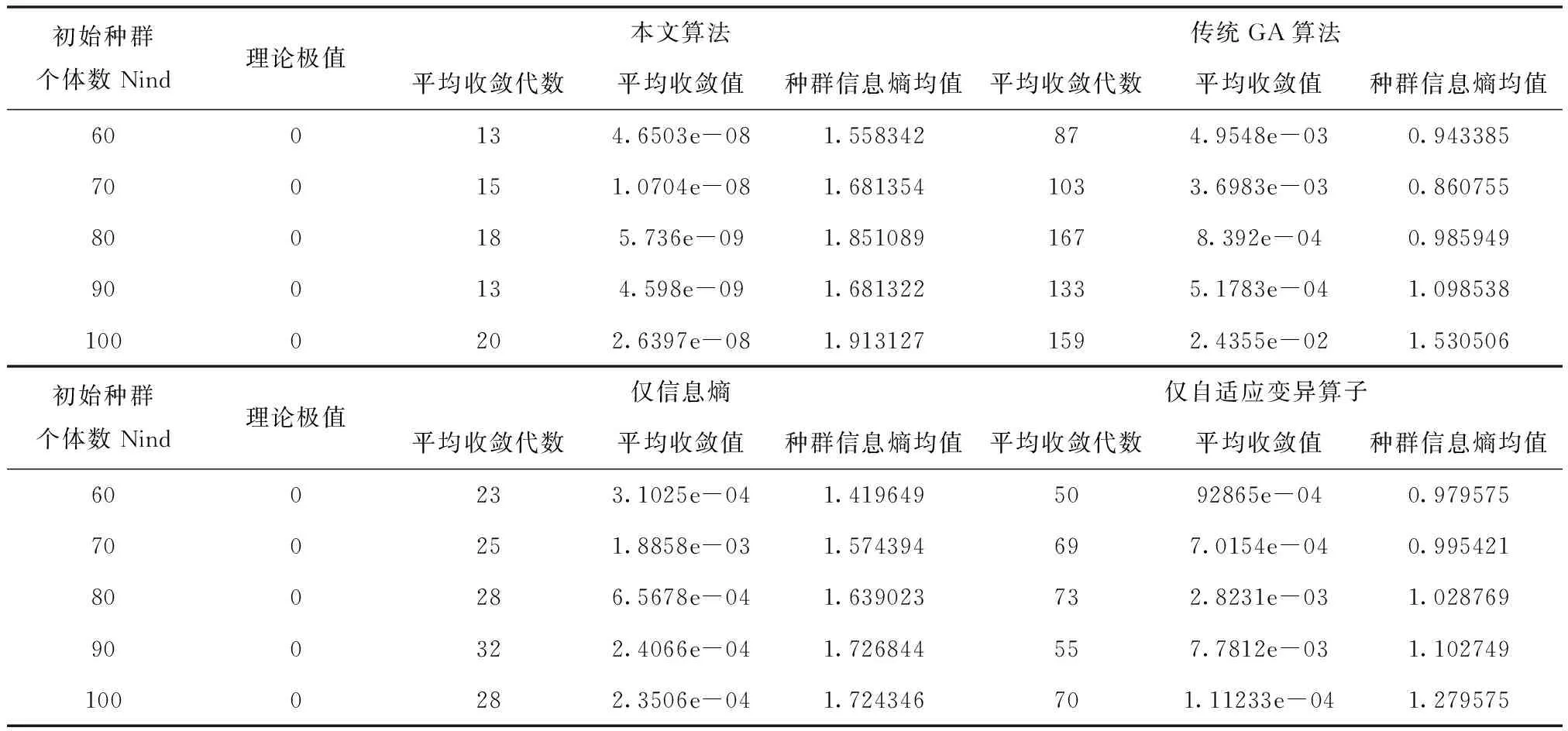
表2 不同初始种群下优化结果对比
由表2可以看出各算法均能对比尔函数进行全局寻优且最终都能收敛至近似全局最优值,虽仍有一定的误差。随着初始种群个数的增加,算法的平均收敛代数总体呈增加的趋势,同时种群信息熵均值逐渐增加。此外本文算法平均只需迭代15次就能收敛至最优解,相比较于传统GA算法收敛速度提升了87%,相较于仅使用信息熵收敛速度提升了41.91%;对比于仅自适应变异算子收敛速度提升了75.58%。同时,收敛精度明显优于其它对比算法。
经过对比实验证明,在测试函数下本文算法在收敛精度和速度上均取得较大提升,算法改进取得较为良好的效果。
5.2 模型求解
5.2.1 基本参数设定
通过统计某工业炸药公司仓库群一段时间内的进出库变化,计算得出每类炸药的出入库频率为fk,某种货物仓库存储总量Ck。如下表3所示,表4为仿真优化的基本参数:
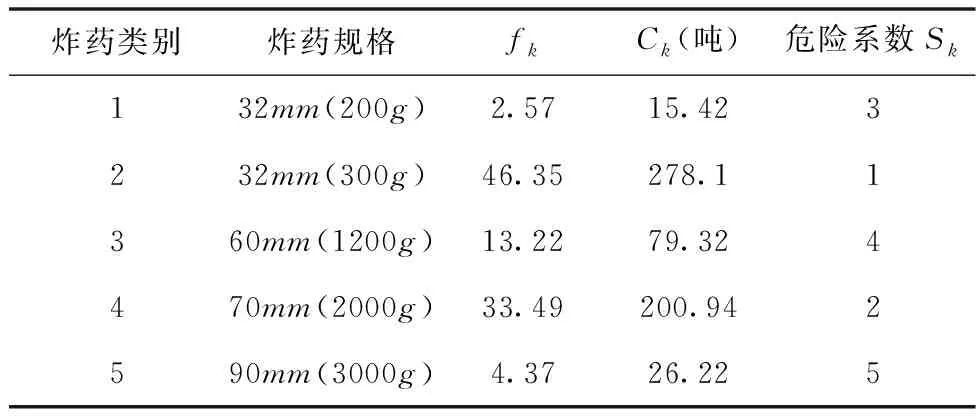
表3 不同规格炸药详细参数
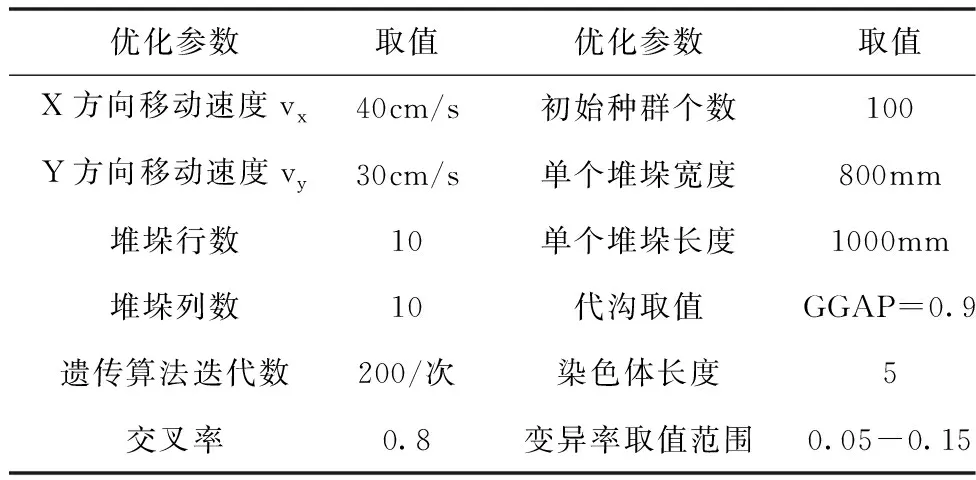
表4 优化仿真基本参数
5.2.2 实验结果分析
本文实验结果由MATLAB仿真实现,带入本文提出的仓储优化模型后进行对比实验,仍采用本文算法、标准GA算法、仅信息熵、仅自适应变异算子四种算法进行求解。以验证改进后的算法对于模型仍具备有效性。
1)仓库群动态分配:设置阈值K1=15,β=3,将fk,Ck带入式(1),(2),(3),(4),得出仓库分配方案(3,7,4,5,8,6,9,1,2,10)即将第2类炸药第1-2个库区内;将第4类和第3类炸药随机放入第3-6库区,即第2和第3座仓库;第1类炸药和第5类炸药随机放入第7-10库区。
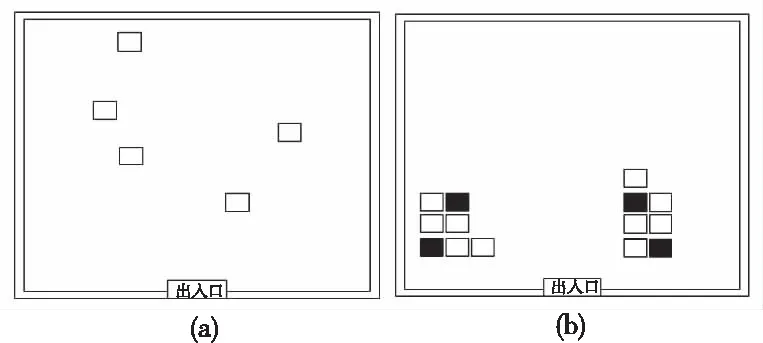
2)仓库内货位动态分配:根据实际情况,模型解空间大小为100,故设置初始种群数量为nind=100,对应信息熵阈值取值为4.5当种群多样性hk 通过随机选取假设(-3,4),(-5,1), (-2,6),(1,3), (3,5),(-4,3),(-5,4),(5,10),(2,1),(4,3)已存放有货物,同时在解空间中随机选取5个坐标作为货位优化前的坐标,进行寻优求解。实验得出结果如下:最优染色体为(-5,5),(-4,5),(-4,4),(-3,5),(-2,5)。即第一个堆垛放入坐标(-5,5)下,以次类推。同时得出目标函数最优值Y=-396.7。其收敛曲线如下图6所示。 图6 模型收敛对比 由图6可以看出,标准遗传算法在迭代至180代时仍不能完全收敛,并且解的质量差。本文改进后的算法在模型中使用取得良好的效果,在20代左右就开始收敛,最终接近全局最优值,解的质量及收敛速度明显优于传统遗传算法。通过对比亦可看出信息熵机制和自适应变异算子的收敛效果亦优于标准遗传算法。其种群信息熵值变化如图7所示。 比较图7可以发现,信息熵作为种群多样性的评价指标,在本文所述模型中依然取得较好的效果。此外使用信息熵机制后,随着迭代次数的上升,相较于标准遗传算法种群信息熵值的变化不会出现断崖式下跌,进而提升算法跳出局部收敛的能力,保证算法的收敛精度及速度。 表5为同一随机坐标下,多次通过改变初代保存位置坐标后,不同的存放方案。从表5中取初始坐标、实验1和实验3画出优化前后的货物坐标如图8所示,其中红色方块代表当前位置已存放有货物。 图8 优化后货物摆放示意图 表5 优化前后坐标变化对比 由表5和图8可以看出,货位优化前布局完全随机,分配杂乱无序,经过货位优化后,货位的分配都尽可能的靠近仓库出入口且与上一次得出的摆放坐标相邻,货位的分配布局变得有序且合理;同时假如存放点已经存放有货物时,算法也能够有效辨别。 从实验结果上来看,利用本文所提算法及模型能够快速找到对应的仓库及库区内的货位,使同种规格的工业炸药产品能够集中存放,且满足先入先出和距离出入口最近的原则。 本文通过对工业炸药仓储过程的特点、难点和要求进行分析,建立了工业炸药仓储优化数学模型;并根据遗传算法对模型求解存在的问题,提出基于信息熵和改进后的自适应变异算子的混合遗传算法;在与遗传算法进行对比后,使用本文算法对模型求解。实验仿真结果表明本文算法相对于标准遗传算法在收敛精度及速度上均有较大提升;同时对于本文的模型求解亦取得了较为良好的效果,能够在一定程度上提高工业炸药仓库群的空间利用率;提高工业炸药产品出入库效率;提升单一仓库内产品存放效率。较好的解决了受工业炸药存放有效期以及存放安全性等约束的优化问题。此外本文在研究过程中对于仓库群的动态分配仅仅只考虑了仓库的分配,对于如何实现货物在仓库群中的动态调配以及闲时优化问题有待进一步研究;对于仓库内货位动态分配如何直接使用多目标优化算法进行求解值得进一步研究。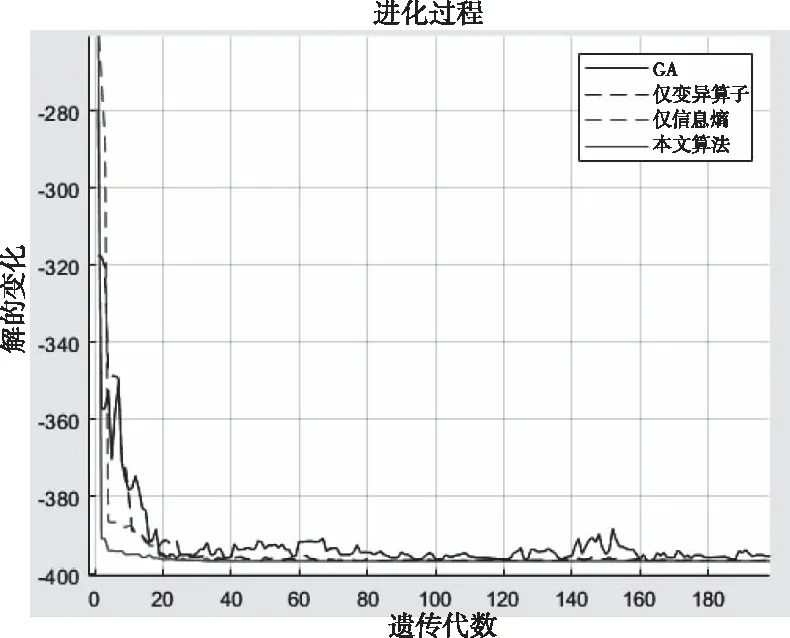

6 结论
