基于小波变换的混沌图像加密算法

李 立,向 菲

(河南科技大学,河南 洛阳 471023)

1 引言

随着互联网的迅速发展,以及物联网、“互联网+”等概念的不断提出,越来越多的人使用多媒体设备。然而在网络传播过程中,这势必会导致各种各样的敏感信息被不法者复制、窃取、篡改的现象,因此图像信息安全技术问题逐渐成为学者们的研究重点之一[1]。在对图像加密的研究过程中,混沌系统相关算法众多,这都是源于其因具有伪随机性、初值敏感性等独特的密码学特点[2]。Robert Matthews首次把混沌系统应用到文本加密中[3],他研究了Logistic混沌映射,提出了一种基于其变形的密钥流生成方法。基于混沌系统处理图像,主要集中在两个方面。空域图像加密方面,文献[4]设计了一种高效的复合型映射,能够有效抵御选择明文和密文的攻击,但是算法最终计算得到的信息熵与理想值差距较大,即加密后的图像随机性不强。文献[5]提出基于Logistic混沌置乱的图像加密算法,该算法简单高效,但是加密图像相邻像素的相关性较大,不能够有效降低明文像素之间的相关性。文献[6]将Logistic映射进行改进,解决了图像相邻像素相关性的问题,但是仍存在加密后的密文图像随机性不强的问题。文献[7]研究了Logistic映射在数字图像加密算法中的应用,说明了混沌映射有着很好的发展前景;同时发现算法运算效率高适用于系统加密,将其应用在机房网络系统能够有效的实现对网络的整体管理,节约了带宽资源。但是由于算法结构简单,抗差分攻击能力不强。而变换域图像加密方面,主要是通过将图像转换到变换域之后再进行加密处理。基于小波变换算法简单、运算速率高等特点,用小波变换处理图像的算法层出不穷。文献[8]通过分析小波变换引出了分数阶小波变换的加密算法,其结果显示加密效果显著。但是仍存在相邻像素之间的相关性变化不大的问题,不能很好地降低图像相关性。文献[9]介绍了一种通过不安全的数据网络或数据库存储进行传输的过程,将虹膜图像中的感兴趣区域在变换域中加密。与基于一维混沌的系统相比,该加密方案增加了密钥空间和高度安全性。文献[10]将小波变换的特点与混沌映射的优点结合,提出一种新的图像压缩与加密方法。将图像从空间域转换为波段转换的频率域,同时混合噪声添加到波段转换的高频部分,不仅减少了密钥消耗和压缩时间消耗,而且提高了解码和重建图像的质量。综上所述,可以得出研究基于小波变换的混沌图像加密不仅可以提高加密算法的效率还能提高加密算法的安全性,有着良好的应用前景。

本文提出了一种将小波变换与改进的二维Logistic混沌映射相结合的图像加密算法。利用小波变换算法简单、运算速率高等特点,首先将明文图像通过小波族db中的“db1”小波函数进行二维单尺度小波变换,接着对变换产生的低频子带系数矩阵和高频系数矩阵进行置乱处理。然后对置乱后的矩阵进行小波逆变换,并使用改进的二维Logistic映射产生混沌系列对逆变换后的加密图像进行扩散处理,实现二次加密产生最终的密文图像。最后对图像加密效果进行安全性分析测试,其仿真结果表明,该算法使用两种置乱方式可以更好地加密置乱明文,同时使用改进的二维Logistic映射和小波变换结合的加密方式使密文敏感度高,能够有效抵御各类攻击。

2 混沌系统与小波变换

2.1 Logistic映射

经典的Logistic映射是由Li-Yorke给出[11],它的公式为

xn+1=λxn(1-xn)

(1)

其中控制参数λ∈[0,4];迭代状态值xn∈[0,1];x0是迭代初值。

Logistic映射存在周期性的混沌现象是由科学家Feigenbaum首次提出的,同时他还指出分岔点的参数值会逐渐形成一个无穷序列,并且存在一个极限值约为3.57,当λ处于这个极限值和4之间时,就会出现混沌现象。随着混沌映射不断被应用于图像加密领域[12],不少学者研究发现一维Logistic映射存在控制参数范围受到限制、点分布不均匀等问题[13]。因此,越来越多的学者开始专注于研究和改进现有的混沌系统和混沌映射。文献[14]中提出一种基于级联调制耦合(CMC)模型的新型二维逻辑ICMIC级联映射(2D-LICM)。根据文章最终的性能评估表明,这种改进的二维Logistic映射具有复杂度大、范围宽等超混沌行为优点。因此本文中采用了这种混沌映射对图像进行扩散处理。它的具体计算公式如下

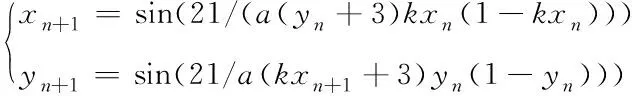
(2)

2.2 小波变换

小波变换是一种针对时间或者空间频率的局部化分析方法[15]。设ψ(t)∈L2(R),其傅里叶变换为ψ(ω),当满足Cψ<∞时称此时的ψ(t)为一个基本小波,其中

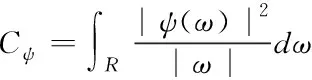
(3)

同其它的变换域方法一样,小波变换也分连续和离散两种。连续时的表达式为:

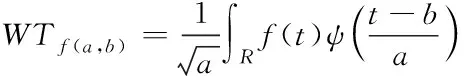
(4)

数字信号处理是在计算机上运行的,因此需要进行离散化处理。而与傅里叶变换不同,小波变换并不是指时间上的连续和离散,离散小波变换就在连续小波变换的基础上对伸缩参数a和平移参数b进行离散化[16]。因此可以得到离散化的表达式

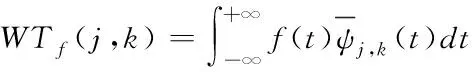
(5)

其中离散小波

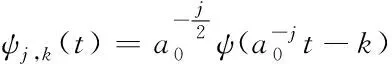
(6)

a0>0且∈C,j、k∈Z。

3 加密过程

本文首先读取目标图像,采用小波族db中的“db1”小波函数对灰度图像进行二维单尺度小波变换;其次,对变换后得到的高低频率系数矩阵进行处理;然后,对加密的矩阵进行小波逆变换实现第一次加密;最后使用改进的二维Logistic映射产生混沌系列进行二次加密产生最终的密文图像。具体的算法实现步骤如下:

1)使用MATLAB软件读取大小为m×n的灰度图像,通过dwt2函数进行二维单尺度小波变换。按照从左到右,从上到下的顺序图像被均分为4个部分,每个部分都是由原灰度图像与一个小波图像内积后,在x和y方向都进行2倍的间隔抽样生成。4个部分的像素值构成对应的高低频系数矩阵。

2)对低频系数矩阵LL、高频系数矩阵HL、LH和HH进行行列置乱处理,其中对低频系数矩阵和LL高频系数矩阵HL、LH通过randsample函数创建行列向量作为指针来达到行列置乱的效果;而对高频系数矩阵HH则通过HL和LH异或的遍历矩阵对其进行分块置乱。在分块置乱部分,创建三个和HH矩阵大小一样的矩阵Alh、Ahl和Ahh以及三个每块含16个像素值分组细胞矩阵Alhf、Ahlf和Ahhf。同时为避免分块环节出现像素除16除不够的现象,对Alh、Ahl和Ahh进行像素补0产生新的矩阵Alht、Ahlt和Ahht。

3)对置乱后的产生的新的频率系数矩阵通过idwt2函数进行二维单尺度小波逆变换,生成第一次加密后的图像。

4) 使用改进的二维Logistic映射公式进行迭代产生混沌系列y1和y2,接着使用y1和y2对第一次加密后的图像进行二次加密,形成最终的密文图像。

加密过程反向操作即可实现解密,得到相应的解密图像。

4 仿真结果及安全性分析

4.1 仿真结果

本文加密系统的仿真测试在64位window11系统,频率为2.90GHz,安装内存为8GB的环境下利用MATLAB 2016b仿真软件256×256的灰度图像进行加密。

映射初始值为: k=0.8,a=0.6,x=0.5,y=0.5。仿真结果如图1所示。

图1 图像加密效果对比

4.2 相邻像素的相关性分析

像素相关性与图像破解密切相关,相关性越高,破解越容易。相关性的计算公式为

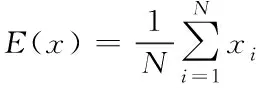
(7)

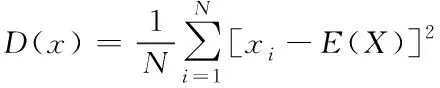
(8)

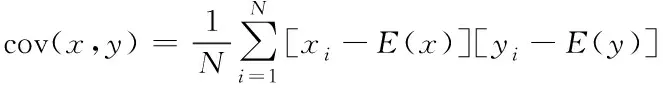
(9)

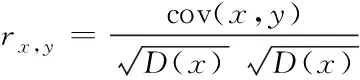
(10)

本文对明文图像和加密图像采用以上的计算公式,得到行、列和对角三个方向上的相关系数,见表1。图2是加密前后对比图。

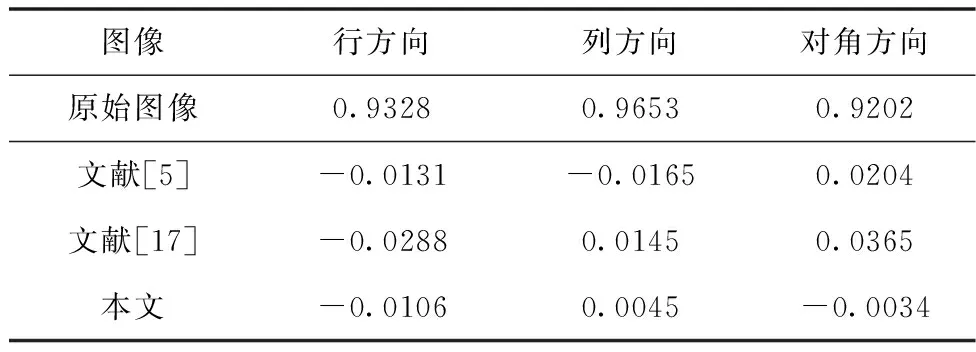
表1 相邻像素相关系数对比

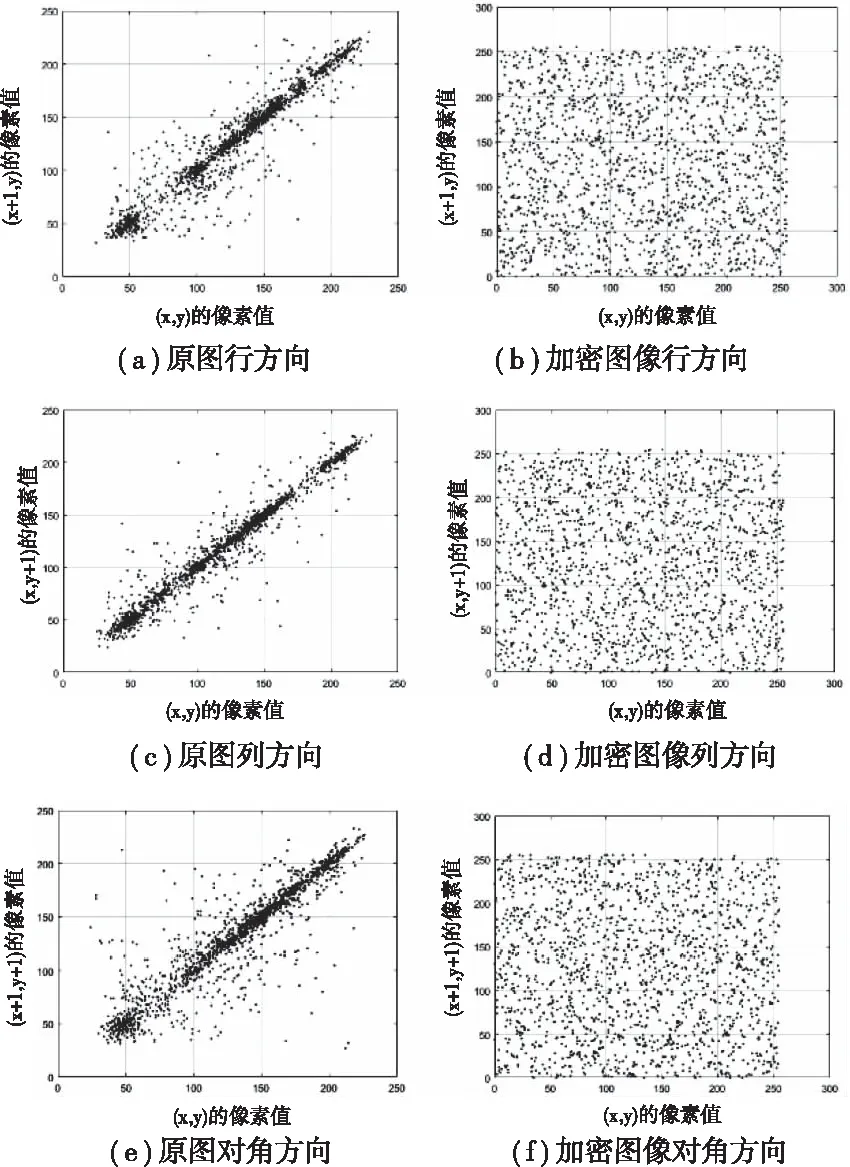
图2 明文与密文相关性对比

表1是本文算法与参考文献的相邻像素相关系数的比较。通过数据可知,原始图像相关系数数值与1接近,故原始图像相关性强。而将表1中的数据结合图2直观可以看出,本文算法加密后的密文图像与文献[5]和文献[17]相比,行、列和对角方向上的相关性与0的差值更小,说明本文算法能够有效降低明文像素之间的相关性。

4.3 直方图分析

直方图将图像中灰度级分布进行统计。直方图分布越均匀则说明图像抗攻击性越强。图3是加密前后的直方图分布。

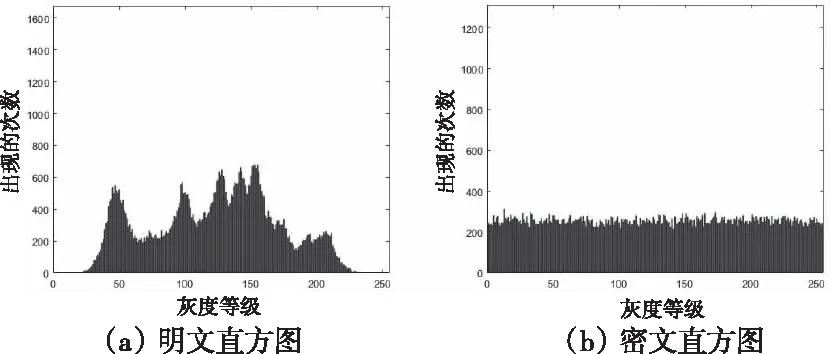
图3 加密前后的直方图分布

4.4 信息熵分析

香农首先提出信息熵的概念,用来反映图像的不确定性[18]。图像信息熵的值越接近理论值则说明该图像信息越不稳定。信息熵的计算公式为

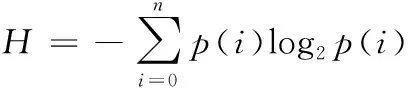
(11)

其中n是灰度等级数,p(i)是灰度值出现的概率。对于n=256的灰度图像理论上的信息熵是8。表2是将本文信息熵与文献[6]和文献[19]进行对比的结果,可以看出本文算法的信息熵更接近理想值,因此可以更好地抵御信息熵攻击。

表2 信息熵对比

4.5 差分攻击分析

差分攻击可以检测算法对明文的敏感性,检测抵御差分攻击的重要指标是像素变化率NPCR和归一化像素平均改变强度UACI[20]。两者的计算公式为

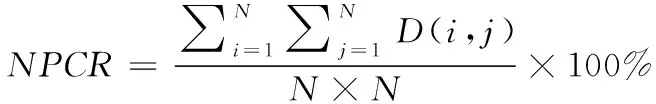
(12)

(13)

其中Ie1(i,j)和Ie2(i,j)是两幅加密图像大小为N×N的Ie1和Ie2中坐标为(i,j)的像素值。如果Ie1(i,j)≠Ie2(i,j),D(i,j)=1,否则D(i,j)=0。

改变明文图像任意一个像素点后,重新加密产生密文图像。对新加密得到的图像与原明文图像加密后的图像进行测试,并利用上述的公式计算得到NPCR数值为0.9958,UACI的数值为0.3368。与文献[5]的对比结果见表3,结果表明本算法更加接近理想值,具有较强的密钥敏感性,能够有效抵御差分攻击。

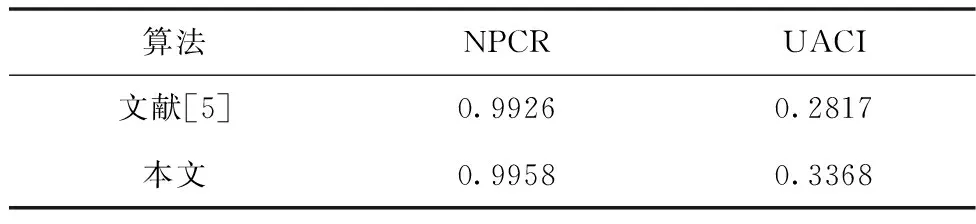
表3 NPCR与UACI对比结果

4.6 密钥空间分析

密钥空间越大,攻击时间和代价就越高。本文算法的密钥包括x,y,a,k,且它们都步长都为10-14,所以可以计算得到密钥空间大小为1014×1014×1014×1014=1056>2100。因此该算法密钥空间大,攻击时间和代价足够高,可以有效抵抗穷举密钥攻击。

4.7 敏感性分析

对事物敏感是指反应迅速敏锐,而一个算法的密钥敏感性则是指对密钥进行很小的变动都会引起结果的很大变化。本文算法的密钥精度是双精度,正确解密的图像以及对四个密钥x,y,a,k分别改变10-14后的解密图像如图4所示。

图4 正确密钥和密钥改变后解密图

5 结论

本文基于小波变换结合混沌映射,通过对小波变换产生的高低频率系数矩阵进行置乱处理实现第一次加密,接着小波逆变换后通过改进的二维Logistic映射对加密图像进行二次加密形成最终的密文图像,并对算法的安全性进行分析。最后按照图像加密效果测试的依据对密文进行仿真检测,相关结果表明,该算法使用两种置乱方式可以更好地加密置乱明文,同时使用改进的二维Logistic映射和小波变换结合的加密方式使密文敏感度高,能够有效抵御各类攻击。