滑雪跳台修整机械臂轨迹控制方法

刘 拓，李艳杰，卜春光，眭 晋，范晓亮

(1.沈阳理工大学机械工程学院，沈阳 110159；2.中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳 110016)

跳台作为空中技巧项目训练、比赛场地的核心设施，对保障运动员训练具有重要作用。 国内外针对跳台修整主要依赖人工。 由于跳台空间跨度大、跳台曲面曲率非线性，人工方法存在以下问题:天气寒冷、修整人员体力消耗大，工作舒适性差；跳台为非线性曲面，仅规定了必要的点位和角度，即关键点表单，没有标准修整曲线，“尺量铲修”的人工修整方法难以保证修整精度，对修整人员的技术要求极高；人工测量难度大，教练员难以定量评估跳台动态变化对运动员训练的影响。

采用机械臂对滑雪跳台的修整需要解决的问题有:一是要建立一条滑雪跳台修整规定的跳台标准曲线；二是针对标准曲线进行轨迹规划，以方便机械臂的修整工作。

针对第一个问题，国内外一般采用样条曲线拟合的解决方案，其中最常用的有三次样条曲线、B 样条曲线和NURBS 曲线等[1]。 Yeh 等[2]采用了最小二乘法将离散的数据点拟合成连续的NURBS 曲线，再样条插补。 Wang 等[3]设计了NURBS 插补器，可以先将多个关键点连成短线段，然后拟合成NURBS 曲线进行插补。 针对NURBS 无法经过部分关键点的问题，袁旭华等[4]通过在B 样条曲线原有控制点上添加新控制点的方式对传统B 样条曲线进行改进，以保证其能通过全部控制点。 董甲甲等[5]通过在B样条曲线上增加型值点的方式，在不损害曲线原有的连续性、凸包性等优点的情况下，提高了曲线的拟合精度。 张跃明等[6]通过对曲率进行约束，实现了多段B 样条曲线的二阶连续。 孔庆博等[7]通过在五次多项式插值的不平滑处引入B 样条插值，使关节运动更加稳定，有效减少了冲击和震动。

针对自由曲线的轨迹规划问题，王旭浩等[8]在相邻轨迹段间采用圆弧模型对衔接拐角处平滑过渡，在给定轨迹衔接点坐标和过渡圆弧半径等参数的情况下，规划出衔接圆弧处的最优速度。倪晓伟等[9]通过使用三次B 样条曲线对多示教点进行拟合，并用复化辛普森积分求取B 样条曲线的曲线长度和姿态转角作为参数进行轨迹规划。 Li 等[10]则是将三次B 样条曲线应用到机械臂抓取和放置运动中，通过限制初始速度、终止速度和加速度实现关节空间下B 样条曲线的轨迹规划。 陆原超等[11]则构造了关节空间下的轨迹规划函数，但该方法只适用于关节空间，无法应用于笛卡尔空间。

基于上述文献，本文将多路径点拟合和自由曲线轨迹规划相结合，提出一种通过多路径点的平滑拟合曲线的梯形波轨迹规划方法，并将该方法运用到滑雪跳台修整，研究内容如下:

1)针对修整作业用机械臂进行运动学建模，通过Matlab 对机械臂运动学模型进行仿真验证；

2)针对滑雪跳台模型基于多关键点表示的特点，采用曲线拟合方法确定跳台修整曲线；

3)针对滑雪跳台修整曲线为多段相连非线性曲线，长度计算困难的问题，提出丈量法结合梯形波的修整轨迹规划方法。

1 修整机械臂运动学建模

建模包括正向运动学模型和逆向运动学模型。 本文研究的修整机械臂为六自由度工业机械臂，正运动学建模通常采用Denavit-Hartenberg(D-H)参数法[12-13]，其逆运动学模型为复杂非线性方程，采用解析方法建立逆向运动学模型。

1.1 D-H 参数确定

修整机械臂本体和关节连杆坐标系定义如图1 所示，图中定义了各关节连杆坐标系的x轴方向和z轴方向，而y轴方向则通过x轴和z轴的方向共同确定。 根据D-H 建模方法，确定的D-H 参数见表1，表中i(i＝1，2，3，4，5，6)为关节连杆编号，θi为绕zi轴、从xi-1轴到xi轴所需的角度，di为沿zi轴、从xi-1轴到xi轴所需的距离，ai-1为沿xi-1轴、从zi-1轴到zi轴所需的距离，αi-1为绕xi-1轴、从zi-1轴到zi轴所需的角度。

表1 机械臂D-H 参数

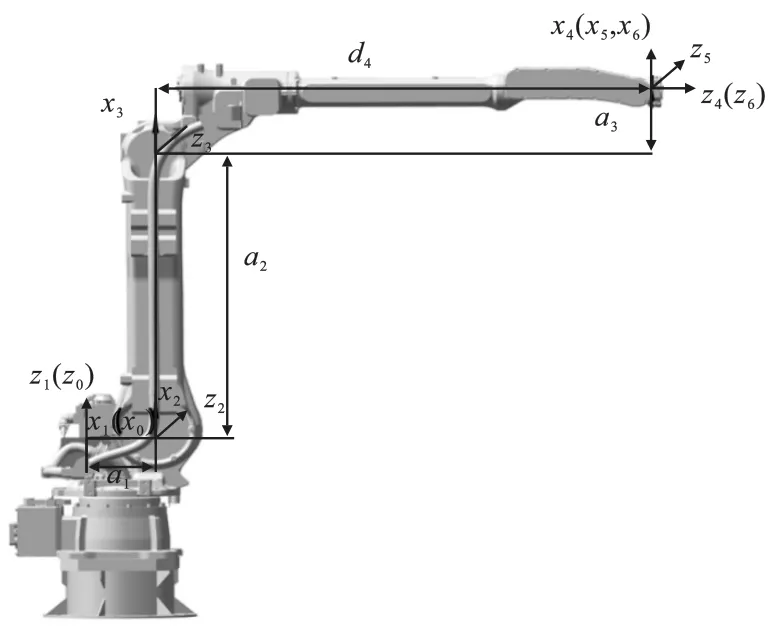
图1 机械臂坐标系及D-H 参数

1.2 正运动学分析

依据表1，可得相邻关节间的坐标变换矩阵[14]如式(1)所示。

其中:

以上表达式即构成了正运动学方程，表示各关节角度到机械臂末端执行点位姿的变换关系。

1.3 逆运动学分析

本文采用解析法进行修整机械臂逆向运动学推导。 对式(2)两边进行逆转换运算，筛选矩阵两端合适的对应元素进行求解，求出各关节角的解。 基于上述思路解得各关节角度的表达式如下。

其中:

以上为机械臂逆运动学的解析解，共存在八组，需要确定最优解，本文使用构型法确定最优解。 根据机械臂六个关节的关节范围，从第一关节开始到机械臂末端进行逐一限定，通过保持构型不变条件，筛选得到最优解，如仍然存在多解，则取上一点角度相近的一组解为最优解。

1.4 机械臂运动学仿真

本文使用Matlab 仿真软件对机械臂的运动学进行验证，分别用Matlab 机器人工具箱和1.2中推导出的机械臂正运动学公式编写脚本，设置一组关节角度值θ＝[0°， -90°，60°，60°， -60°，-60°]，其结果对比如图2 所示。

图2 正运动学验证

图2中modt06 为机器人工具箱所得正运动学矩阵，modmyt06 为利用机械臂正运动学公式得到的结果，从图2 中可以看出两者保持一致，证明了1.2 中推导的正运动学公式的有效性。

将图2 中的正运动学矩阵代入机械臂逆运动学方程中，可得出针对该姿态矩阵的解析解，其结果如图3 所示。

图3 逆运动学验证

图3中ikine_t 为逆运动学给出的之前由正运动学得出的位姿矩阵的八组解，而ik06 为从该组解中选出的最优解，其在八组解中的位置图中加粗表示，其结果和正运动学验证中预先设置的角度θ相同，由此验证了该逆运动学算法的正确性。

2 跳台修整曲线拟合

图4所示为体育部门提供的滑雪跳台修整的标准模型，表2 为滑雪跳台的关键点表单。 为适应机器人修整轨迹控制需要，本文需要利用关键点拟合确定跳台修整曲线，考虑跳台为柱体形状，截面曲线形状相同，利用修整曲线沿着跳台宽度方向移动，可得到覆盖跳台的全部修整曲线。

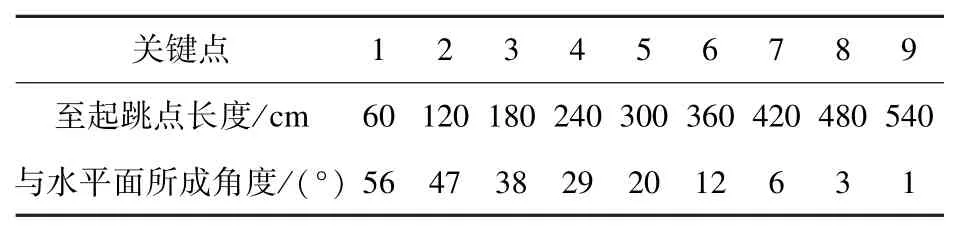
表2 关键点表单

图4 滑雪跳台修整标准模型

为确保拟合后的跳台曲线能经过关键点，本文在每两个相邻的关键点之间建立一条三阶贝塞尔曲线，即三个关键点由两条贝塞尔曲线连接，其中间的关键点为两条曲线交点。 一条三阶贝塞尔曲线由首尾点和两个控制点组成，相邻关键点为其首尾点，以两条贝塞尔曲线在交点处一阶导数相等为限制条件，确定其与交点相邻的控制点，从而确定各条三阶贝塞尔曲线。 确定贝塞尔曲线控制点的过程如图5 所示。

图5 贝塞尔曲线确定控制点

假设P0和Pn为图4 中跳台的关键点9 和跳台终点，Pi-2、Pi-1、Pi、Pi＋1、Pi＋2均为跳台控制点，也为两条三阶贝塞尔曲线的交点。 以Pi为例，若达到其两端的两条三阶贝塞尔曲线在该点处平滑，要求两曲线在该点的切线斜率相同，则过Pi点作曲线的切线，将位于Pi左侧的贝塞尔曲线控制点Bi-1和位于Pi右侧的贝塞尔曲线控制点Ai均取在过Pi点所作的切线上。 连接Pi-1和Pi＋1作直线，使过Pi点的切线的斜率与直线Pi-1Pi＋1的斜率相等，此时控制点Ai、Bi-1的坐标可以表示为

式中:(xi-1，yi-1)、(xi，yi)、(xi＋1，yi＋1)分别为Pi-1、Pi和Pi＋1坐标；k1、k2为任意给定的正数。

同理可以得到Pi-1两侧控制点Ai-1、Bi-2。 通过Pi、Pi-1、Ai-1和Bi-1可确定Pi和Pi-1两点之间的三阶贝塞尔曲线。

通过上述方法，可以获得包括跳台终点在内的10 个关键点形成的9 条曲线中的7 条。 但也存在特殊情况，在求取P0右侧控制点A0时，如使用公式(30)，则需要P0左侧存在关键点P-1，但P-1点不存在，因此需要用P0的值作为P-1的值，可得P0右侧控制点A0的坐标为

式中:(x0，y0)、(x1，y1)分别为P0、P1的坐标；k0为任意给定的正数。

同理，在求取Pn的左侧控制点Bn-1时，如使用公式(31)，则需要关键点Pn的右侧存在关键点Pn＋1，该点同样不存在。 因此需要用Pn的值作为Pn＋1的值，可得Pn左侧控制点Bn-1的坐标为

式中:(xn，yn)、(xn-1，yn-1)分别为Pn、Pn-1的坐标；kn为任意给定的正数。

通过上述方法得到滑雪跳台的参考曲线如图6 所示。

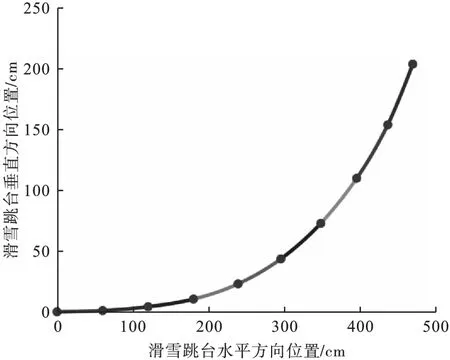
图6 滑雪跳台参考曲线

由图6 可见，整个曲线由9 段不同曲线组成，其整体首尾相连，其中实心点为关键点。 根据该曲线得出的跳台三维模型如图7 所示。

3 跳台修整轨迹规划算法

机器人修整轨迹规划是在保证运动速度平滑的前提条件下，确定修整机械臂在每个运动控制周期的位姿，以实现跳台修整的精确性、修整运动的稳定性和机械臂的安全性。

因为整体曲线是由多段三阶贝塞尔曲线拟合而成，所以需要进行整体曲线的速度规划，不能分段规划，否则在两段曲线的连接点处会出现速度不一致的问题，为此本文提出采用丈量法进行修整轨迹规划。

丈量法是利用基于梯形波速度规划确定的轨迹点间隔为半径，通过丈量圆与修整曲线的交点确定机械臂修整运动轨迹的方法。 丈量法实现简单，不仅满足了速度平滑要求，同时也避免了非线性贝塞尔曲线求解曲线长度的难题。 基于丈量法的修整轨迹规划算法示意图如图8 所示。

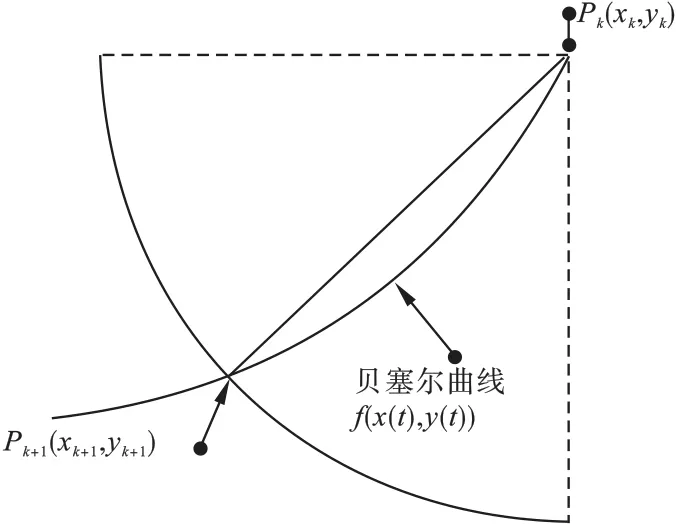
图8 丈量法示意图

在运用丈量法过程中，首先需要确定丈量圆的原点和半径。 设跳台修整曲线上某点Pk(xk，yk)为丈量圆原点，为确定丈量圆半径，假设速度为v，给定加速度为a，给定时间间隔为te，最大速度为vmax。 基于梯形波规划的机械臂修整轨迹方程为

式(37)中基于梯形波速度规划确定的轨迹点间隔长度s即为丈量圆的半径。

在得到原点和丈量圆的半径后，以Pk(xk，yk)为圆心，以s为半径画圆，该丈量圆与贝塞尔曲线f(x(t)，y(t))相交，可得以当前贝塞尔曲线参数t为未知数的一元二次方程式如下。

采用牛顿迭代法[15]对式(38)进行求解得出未知数t的当前值，将其代入当前贝塞尔曲线参数方程即可得出该圆弧与当前贝塞尔曲线f(x(t)，y(t))的交点，记为Pk＋1(xk＋1，yk＋1)，即符合梯形加减速轨迹规划的轨迹点。

以点Pk＋1(xk＋1，yk＋1)为新的原点，以新的轨迹间隔长度为半径，可得新的交点，重复这一过程得出整条曲线的速度轨迹，且速度变化符合梯形加减速变化。

因为跳台修整曲线由多段三阶贝塞尔曲线头尾相连，所以当丈量法进行到两段三阶贝塞尔曲线的交点处时，因半径长度大于圆心到该段曲线末点的距离，故无法产生有效交点，此时应以该点为圆心，以当前路程为半径画圆，求与下一段三阶贝塞尔曲线的交点，以解决由多段贝塞尔曲线连接构成的修整曲线的轨迹规划问题。

针对上述算法，利用Matlab 软件画出滑雪跳台轨迹规划曲线，如图9 所示。

图9 滑雪跳台轨迹规划曲线

由图9 可知，通过丈量法进行轨迹规划的曲线与图6 所示滑雪跳台参考曲线保持一致，其整体轨迹误差值保持在0.02 mm 以内。 其速度和加速度曲线分别如图10 和图11 所示。

图10 轨迹规划速度曲线

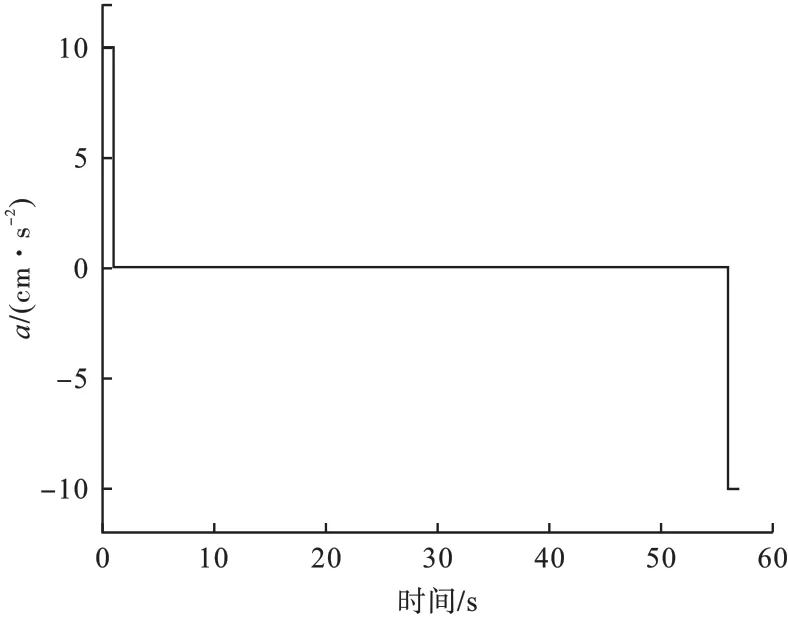
图11 轨迹规划加速度曲线

从图10 和图11 可以看出，轨迹规划后整体速度符合梯形加减速的要求。

4 实验与分析

4.1 实验系统与流程

在仿真验证的基础上，课题组在沈阳市白清寨空中技巧训练基地通过现场应用试验，对自由式滑雪跳台修整机械臂轨迹控制算法进行测试。测试结果通过量测和目视两种方法确定。

如图12 所示，试验用滑雪跳台为自由式滑雪跳台的单周台，该滑雪跳台的关键点表单如表2所示。 本文实验系统由移动平台、机械臂和修整工具、视觉定位系统、地面指挥系统构成。

实验过程如下:

1)控制机器人进入试验场地、接近单周跳台，使跳台处于修整机械臂工作空间内；

2)开启视觉定位系统测量跳台位姿，将位姿数据发送给机械臂；

3)控制机械臂以直线运动方式移动到目标修整点；4)控制机械臂开始进行滑雪跳台修整作业；5)作业结束后，机械臂自动回到工作姿态。

4.2 实验结果与分析

图13所示为一条轨迹修整完成后的跳台，其中数字1 为机械臂修整跳台曲面，数字2 为人工修整跳台曲面。

图13 机械臂实际修整雪面

1)量测法。 采用人工修整测量，用高精度水平仪针对滑雪跳台机器人修整的曲面进行测量。高精度数显水平仪如图14 所示，水平尺的长度为60 cm。

图14 高精度数显水平仪

对应图4 中各关键点测量得到的相对大地水平面的角度值见表3。

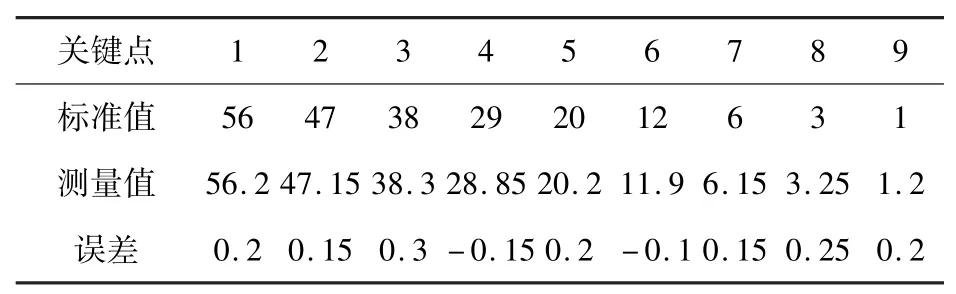
表3 量测法误差(°)

人工修整标准要求关键点角度误差小于正负0.3°。 由表2 可见，全部关键点的角度值误差均小于人工修整误差的要求。 量测法显示，机器人修整误差满足修整精度要求。

2)目视法。 图13 为机械臂修整与人工修整的效果对比，从图中可以明显看出，人工修整的跳台表面相对粗糙，整体可见起伏，而机械臂修整的跳台表面平滑、整体无可见起伏，目视结果显示，机器人修整效果优于人工。

综合量测、目视两种方法的评估，表明机械臂跳台修整效果优于人工方法，本文自由式滑雪跳台修整机械臂轨迹控制方法有效。

5 结论

针对自由式滑雪跳台修整自动化需要，研究了机械臂轨迹控制算法。

1)采用三阶贝塞尔曲线拟合方法，将由关键点表达的标准跳台模型转换为由曲线表示的跳台模型。

2)针对由多段贝塞尔曲线构成的修整曲线，研究了丈量法轨迹规划算法，降低了规划难度。

3)采用D-H 建模方法，建立了修整机械臂的正逆运动学模型，打通了机械臂轨迹规划和控制的通道。

4)借助视觉定位技术，进行了跳台修整控制算法的现场测试并对比人工修整效果，验证了机械臂修整轨迹控制研究的有效性。