基于DEM的Priority-flood并行填洼算法优化

王朔,修佳鹏,杨正球

(北京邮电大学 计算机学院(国家示范性软件学院),北京 100089)

0 引言

数字高程模型(digital elevation model,DEM)是存储为浮点或整数值的矩形阵列,用来表示地面高程的一种实体地面模型。越来越多学者将DEM用于提取某一地区的水文和地貌特征。洼地指近似封闭的比周围地面低的地形,在DEM中体现为一块区域的高程完全被其相邻的较高高程包围,如图1(a)所示,黄色的单元即为洼地。有些洼地是真实的自然地形,但大多数的洼地是伪洼地,因DEM收集和处理中的技术问题产生[1]。

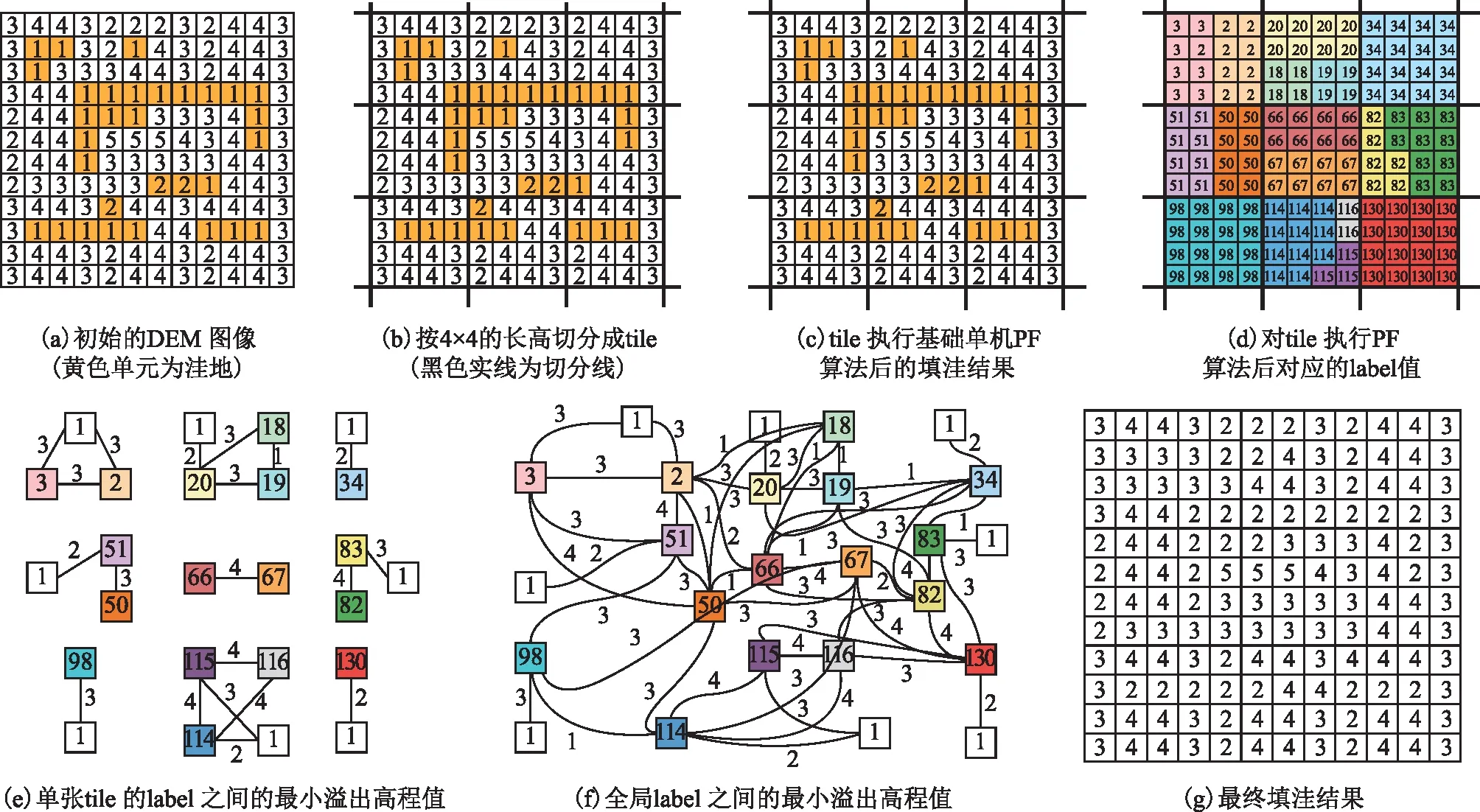
注:流向同一边缘点的单元label一致,label 1为环绕DEM的低地势点,连接label 1的都是DEM边缘点label。图1 平行PF算法示意图

因DEM中存在洼地或伪洼地,在进行水文分析时,二者都会使DEM中的水流方向不能判断或水流逆流,导致大部分水文提取算法无法直接依据DEM进行计算[2]。所以首先要对DEM进行填洼,这是水文分析的必要预处理[3]。

填洼指填充洼地,在DEM中通过提高单元的高程值使得洼地得以填充,从而获得平整的土地,使得DEM中任何单元都有一条通向DEM边界的非上升路径[4],图1(g)即为填洼后的DEM。近年来,许多填洼算法被提出并应用,其中有3类最具代表性[5]。第一类是J&D算法[6],先扫描 DEM识别出其中的洼地,然后将洼地提升相邻单元中高程值最低者,但该类算法的时间复杂度过高,为O(N2)。第二类是P&D算法[7]。该算法以一极大高程值水面淹没整个DEM,在水流可流出的前提下,不断迭代去除多余的水,直到每个单元的高程都具有到相邻单元的下坡。理论上,P&D算法最坏情况的时间复杂度为O(N1.5),相比J&D算法,降低了时间成本。第三类算法[8-11],即Priority-Flood(PF)算法。该算法引入优先队列这一数据结构,队列内高程值递增排列。首先将DEM的所有边缘单元入队,再将它们依次出队,对出队单元的相邻单元进行填洼,然后将相邻单元入队,直到队列为空,算法结束。对于浮点数据,该算法的时间复杂度为O(NlogN),对于整形数据,该算法的时间复杂度为O(N),相较于J&D和P&D算法,大大缩短了时间成本。

如果单张DEM可以完全适应计算机的内存(random access memory,RAM),那么上述3种算法都可以有效地执行填洼操作。但随着机载激光雷达技术的发展,DEM的分辨率不断提高,分辨率高达1 m或万亿单元的超大规模DEM已可以获取。虽然计算机的处理性能和内存显著增加,但增速远远低于DEM数据规模增速,DEM通常不能适应一台普通计算机的RAM[12],则现有的3类单机串行填洼算法无法实施填洼。

1 并行PF算法

针对单机串行填洼的缺陷,许多学者提出了J&D算法、P&D算法的并行化。但对于效率最高的PF算法,受限于洼地可能横跨切分区域,直到2016年才由Richard Barnes提出了PF算法的并行实现。该并行算法的执行效率高于原PF算法,同时实现了大尺度DEM的填洼,该算法成功对2万亿单元DEM进行填洼,这个测试集比以前文献中的任何测试都要大3个数量级,但计算时间只增加了1～2个数量级,是目前效率最高的平行填洼算法。图1描述了该算法的全过程。首先,将单张DEM按指定长高切分为多张小尺度的、可以适应内存的虚拟图块(tile)。如图1(b)所示,切分时遇到了并行填洼最为棘手的情况:一块洼地被切分到了多张tile里。该算法分为3个阶段进行计算。

第一阶段,处理单张瓦片(tile)。生产者(producer)将tile分配给各个消费者(consumers)节点,各节点依据文献[12]的algorithm 1对所有tile并行执行基础PF算法,得到每个tile填洼后的高程值(非全局的填洼结果)。将所有流向该tile同一边缘点的单元都标记相同的标签(label),同时得到label之间的最小溢出高程值映射(assMap)。最小溢出高程值的定义见式(1)。

assMapLabelA_LabelB=min{max(demc,demn)|c∈LabelA,n∈LabelB且n∈c的邻点}

(1)

式中:c和n是属于dem的两个栅格点;demc和demn分别指c点和n点在dem的高程值;assMapLabelA_LabelB指水流如果在LabelA与LbaelB间流动应满足的最小高程值。

第二阶段,处理边缘。依据文献[12]的algorithm 2,通过tile之间的相邻边,关联起tile与tile之间label的最小溢出高程值,由此得到了全局label间的最小溢出高程(globalAssMap)。

第三阶段,对globalAssMap执行PF算法,得到每个label应填洼到的最小高程值labelWithMin,并将tile中所有label所属单元提升到该label对应的labelWithMin值。此时的tile即为填洼后的最终结果。可以根据用户需求将tile合并成一张总的DEM,或者直接将tile分块存放。

2 Barnes并行PF算法的优化

本文基于Barnes的并行PF算法(简称原算法),针对输入为一张大尺度DEM的场景,在切分策略及label的标记策略提出优化(简称优化算法)。将原算法第一、第二阶段的所有操作都限制在一张tile,而无需等待其他tile构建完毕,节省了原算法需要跨8张tile处理边缘边和构建全局映射所消耗的时间,从而提高算法的整体效率。

2.1 带halo的切分策略

原算法在DEM切分tile的时候,严格按tile指定的长和高进行切分,见图1(b)。本文提出一种带光环(halo)的切分方法。halo是以tile为中心,来自其相邻的8个tile的相邻单元格,值为高程值,这些额外的单元像光环一样围绕在原始tile周围。halo和tile的边缘边(edge)各为4条边。以图2为例,以4×4为尺寸进行DEM切分,切分为了9张tile,以tile4为例,黄色区域即tile4的halo,紫色区域为tile4的edge,紫色区域加蓝色区域即为tile,tile加黄色区域即为tileWithHalo。tileWithHalo里存在12个四角点(corner),corner是指tile中的左上、右上、左下、右下4个顶点,依次定义为corner0、corner1、corner2、corner3。如图2所示,包括tile的4个corner以及相邻tile的8个corner,分别位于edge与halo。若指定tile的尺寸为a×a,经此切分策略切分后,tileWithHalo的尺寸为(a+2)×(a+2)。

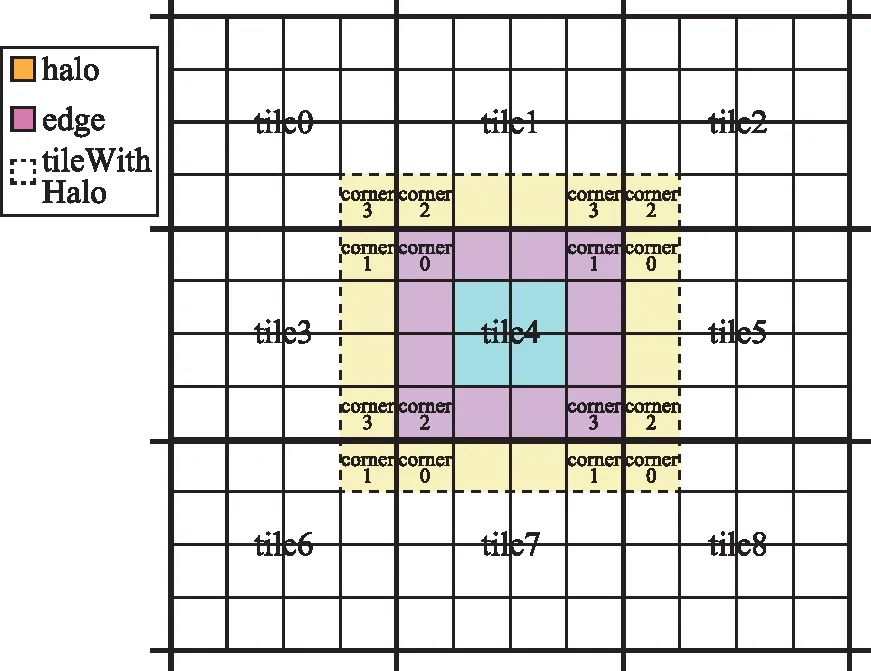
图2 带halo的切分策略

2.2 label的标记及globalAssMap构建

原算法要等所有tile都执行完毕PF算法,再去其他节点寻找该tile的相邻8个tile来构建全局的globalAssMap。是同步操作,因等待其他tile执行完毕,会消耗过多时间。

优化算法经过2.1节的切分策略得到tileWithHalo,tileWithHalo已经带有相邻8个tile的edge,所以在构建globalAssMap的过程中,只要按照一定的label的标记策略,根据halo计算出相邻tile的edge的label值,就可以将原算法的第一、第二阶段整合,将所有操作限制在一张tileWithHalo中进行,不涉及其他tile或其他节点,也不需要等待所有tile构建完毕再去构建globalAssMap。具体的标记策略如下。

步骤1:计算tile的label起始值(startNum)。对每个tile分配唯一值num,每个tile最大label数量为tileSize×4个。当num等于0时,若label从0开始标记,会与1冲突,因为1已经置为了DEM边缘低地势点label,为保证label唯一性,统一定义为偏移2个数值,每个tile的startNum为num×tileSize×4+2。

步骤2:计算corner的label值。corner的label值是固定的,要保证edge的corner label值和相邻tileWithHalo中通过halo算出的label值一一对应。本文赋予corner一个固定值(式(2)),labelcornern为该label对应4个corner的值,可以推出相邻tile的8个corner的label值。以tile4为例,计算出tile4及相邻tile的startNum后,其corner值见式(3),startNumtilen对应tile下的startNum。

(2)

(3)

步骤3:计算edge非corner的label值。要保证tileWithHalo通过edge计算的label值和相邻tileWithHalo中通过halo算出的label值一一对应。以tile4为例,tile4的labeledge_top每个单元和tile2的labelhalo_bottom都相等。若以计算corner的方式给edge中每个非corner一个固定的label值,这样虽然简单易行,但会产生过多的label值,影响算法的效率。本文通过优先队列,设定startNum+4、startNum+4+(edgeSize-2)、startNum+4+(edgeSize-2)×2、startNum+4+(edgeSize-2)×3分别为上、下、左、右4条edge的非corner的起始label(startLabel),如式(4)所示,startLabeln表示该tile对应边缘边的起始label,为减少label值,且保证流向tile同一边缘点的单元label值相同,本文设计PFBORD算法,将edges所有单元分别进入一个最小优先队列,见algorithum 3。

(4)

algorithm 3 PFBORDInput: Q, tileWithHalo, labels, startLabelOutput: labels1:whileQ 不为空 do2:c ← Q.pop3: iflabels(c) == 0then4:foreach n ∈ c 的邻点且同为 edge 或同为 halo do

步骤4:计算halo非corner的label值。要保证tileWithHalo通过halo计算的label值和相邻tileWithHalo中通过edge算出的label值一一对应。流程同步骤3,但startLabel与edge不同,以tile4为例,如式(5)所示,需要与相邻tileWithHalo的edge对应。将4条halo分别进入最小优先队列,注意此时的halo要剔除左上、右上、左下、右下tile的corner点,然后执行PFBORD算法。

(5)

步骤5:构建globalAssMap。首先对tile执行基础PF算法,得到:tile填洼后的高程值(非全局填洼结果),存放在tileWithHalo中;tile所有单元的label;tile的assMap。由于halo的label相同于相邻tile edge的label,所以通过tileWithHalo构建edge与halo label的assMap,即可把相邻tile相关联,与原算法的第二阶段达到的结果一致。最后,将所有tileWithHalo的assMap进行合并即为globalAssMap。

经过以上5步,得到关键的globalAssMap,接下来的步骤与原算法一致,本过程的伪代码见algorithm 4。图3描述了优化算法的整体流程。

algorithm 4 label 的标记及 globalAssMap 构建输入: tileWithHalo,tileSize,tileOff,offStartNum输出: assMap,labels,tileWithHalo1: 定义二维数组 labels 且与 tileWithHalo 维度相同,初始值置为 02: 定义 assMap 为空 Map3: 定义 Q1,Q2,Q3,Q4 为最小优先队列4: 根据 tileOff 找到该tile相邻的8个tile的tileOff,再根据offStartNum找到相邻的8个 tile。

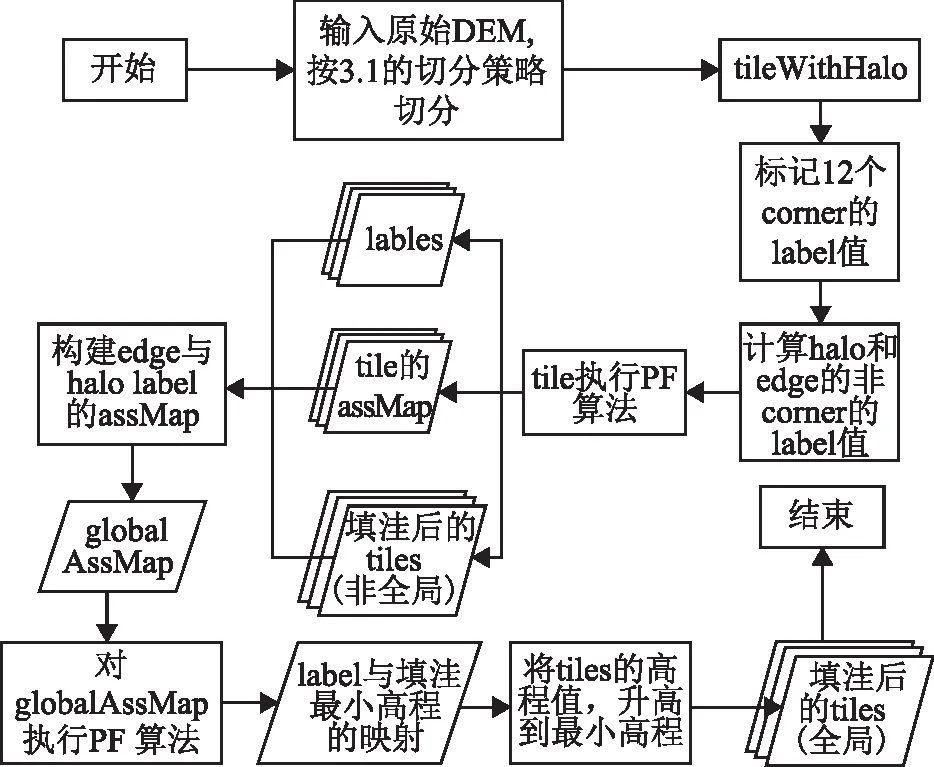
图3 优化算法流程

2.3 优化算法的Spark实现

原算法与优化算法,实际上是两个MapReduce过程,可以通过OpenMP、MPI、Spark等技术实现,原文选择了MPI进行实现。MPI的语言更原生,速度更快,但是代码量巨大,非常繁琐,在接口的易用性上,也低于spark。用spark来实现原算法及优化算法,可为并行填洼算法提供一个新的解决方案。

spark是大数据领域基于内存的快速而通用的计算引擎。弹性分布式数据集(resilient distributed datasets,RDD)是spark的基本数据结构,是位于内存中的对象集合,同时可以将每个RDD分成多个分区,不同的分区保存在不同的集群节点上。同时,spark为用户提供了丰富的算子对RDD进行操作。优化算法的spark实现,就是将数据抽象成RDD并进行操作,在由一个主节点(master)和多个从节点(slave)的集群中,以经纬1°作为DEM划分tile的范围,tileSize为tile的尺寸,整个优化算法的伪代码见algorithm5。

algorithm 5 优化算法主流程输入: DEM,tileSize输出: 填洼后的 tile1: 定义 numOff为 Map //tile 与经纬度的映射2: 定义 offStartNum 为 Map //经纬度与 Label 起始值的映射3: 获取 DEM 的维度范围 (xStart, xend)4: 获取 DEM 的经度范围 (yStart, yend)5: num ← -16: forx = xStart to xenddo7:fory = yStart to yenddo8:num ← num + 19:numOff.put(num,(x, y))10:offStartNum.put((x, y), num * 4 * tile-Size + 2)//每个 tile 的 label 起始值11: end for12: end for

3 实验与分析

本文在spark3.1.1集群上,验证优化算法的正确性及高效性,集群配置如表1所示,采用GDAL2.4开源库,选取了3个数据集,分别在正确性、执行时间上将原算法与本算法进行对比。

表1 spark集群配置

3.1 测试数据集

测试数据集覆盖了中国经度73°E～135°E,纬度18°N～53°N的区域,在此区域分别选取10 m、30 m、90 m分辨率的DEM数据,3个数据集的信息见表2。

表2 测试数据集

3.2 正确性实验

将优化算法分别与原算法、单机PF算法对比,来验证优化算法填洼结果的正确性。首先,分别用3种算法进行填洼,得到每个tile填洼后的结果,再将tile合并成整张DEM,分别记为DEMoptimize_n、DEMoriginal_n、DEMsingle_n,其中n为DEM里所有单元数。将DEMoptimize_n分别与DEMoriginal_n、DEMsingle_n对应相等的单元高程值一一相减,若差值和为0,则说明两种算法得到的结果一致,优化算法能得到正确的结果。因为单机PF算法不支持大分辨率的数据集,所以只能在small数据集上对比,n为1.3×107,见式(6),result表示结果差值,tileoptimize_n、tileoriginal_n、tilesingle_n分别表示n点在优化算法、原算法、单机串行算法的高程值。对比结果见表3、表4,可以得到result=0,从而验证优化算法的填洼结果正确。

表3 优化算法与原算法的正确性对比

表4 优化算法与单机PF算法的正确性对比

(tileoptimize_n-tilesingle_n)] (6)

(6)

3.3 执行时间

选取10 m、30 m、90 m数据集,在集群分别执行优化算法与原算法进行填洼,各执行3次,取3次的平均值作为执行时间。将执行时间进行对比,来验证优化算法效率优于原算法,结果如图4所示。由分析可知,优化算法在3个数据集都至少减少14%的执行时间,在10 m数据集优化效果最明显,减少了约37%。效率优化体现在label的标记及globalAssMap构建上,原算法是同步的,而优化算法是异步的,优化算法将所有的操作限制在一张tileWithHalo上,无需等待相邻tile构建完毕再去遍历。

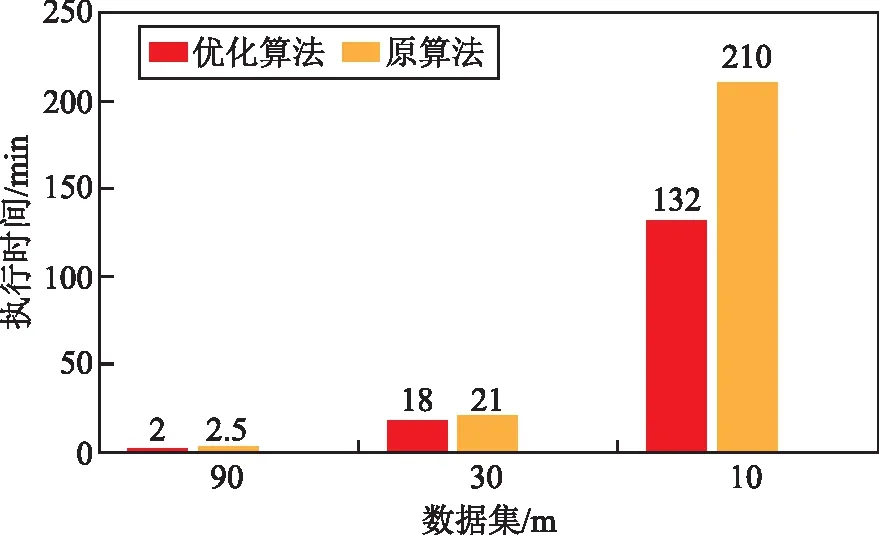
图4 执行时间对比结果

优化效果在小数据集体现并不明显,这是因为优化算法halo的切分策略及label标记也会增加少量耗时。在数据集小的情况下,单张tile仅有144万的单元点,同步异步构建并不会出现较大时间差。优化算法更适用于需要大量label标记或切分tile较多、构建globalAssMap需要等待相邻tile的执行结果的场景,优化算法异步的优势才会体现得更为明显。

4 结束语

随着机载激光雷达技术的发展,DEM规模的增速远远大于普通计算机RAM的增速,若单张DEM不能完全适应RAM,则传统的单机PF算法无法进行填洼。Barnes提出的并行PF算法解决了上述问题。本文基于此并行PF算法,针对输入一张大规模DEM且未进行划分的情况,提出了带光环的划分策略,将相邻tile的边缘边划入到一张tileWithHalo中,由此可以优化原算法的第一、第二阶段,将label的标记及globalAssMap构建完全限制在一张tileWithHalo进行操作,节约了等待相邻tile构建完毕及遍历相邻tile的时间。在填洼实验中,3个测试数据集都至少减少14%的执行时间。通过本文的研究,提高了并行填洼的计算效率,为并行填洼提供了新的视角和方法。