基于光滑整形的钢包快速精准定位研究*

聂国强 孟文俊 廖宣琳

太原科技大学 太原 030024

0 引言

铸造起重机是钢铁冶炼厂的主要生产设备，主要用于转炉加料以及转炉时勾兑铁水。在将钢包吊运至精炼炉或连铸回转台时，将盛有金属液的钢包迅速吊运至浇铸口的上方进行浇铸，此过程要求起重机的动作迅速且精准。由于钢丝绳存在摆动现象，较轻时会延长起重机的运行时间，造成钢水过早的冷却，降低产品的质量和工作效率；严重时会导致金属液溅到浇铸口外，引发安全事故[1]。钢水在吊运过程中由钢包的周期性摆动所激励而产生晃动，反过来又造成钢包负载重心发生偏移，这种影响对其吊运系统的防摇、精确定位、大小车运行及浇注等后续工艺流程都会产生不利影响。目前，针对钢包吊运系统防摇控制的研究很少，多是在传统起重机防摇的基础上加一个干扰信号去模拟刚睡晃动的影响[2，3]。随着智能化时代的到来，铸造起重机也将逐步实现无人化，钢包吊运系统作为重要的一环，其系统的表现显得越来越重要。因此，建立相对准确地数学模型以及为其精准定位控制至关重要。针对这一问题，本文基于等效力学原理建立了钢包吊摆系统的物理模型，基于拉格朗日方程推导出其运动方程，并在该运动方程的基础上设计了级联光滑整形控制器。

1 等效力学建模

根据等效力学原理，本文采用一系列质量－弹簧－阻尼构成的等效力学模型模拟近似钢包内钢水晃动的情况。图1 所示质量－弹簧－阻尼中的每一个都代表了钢水的各个模态。

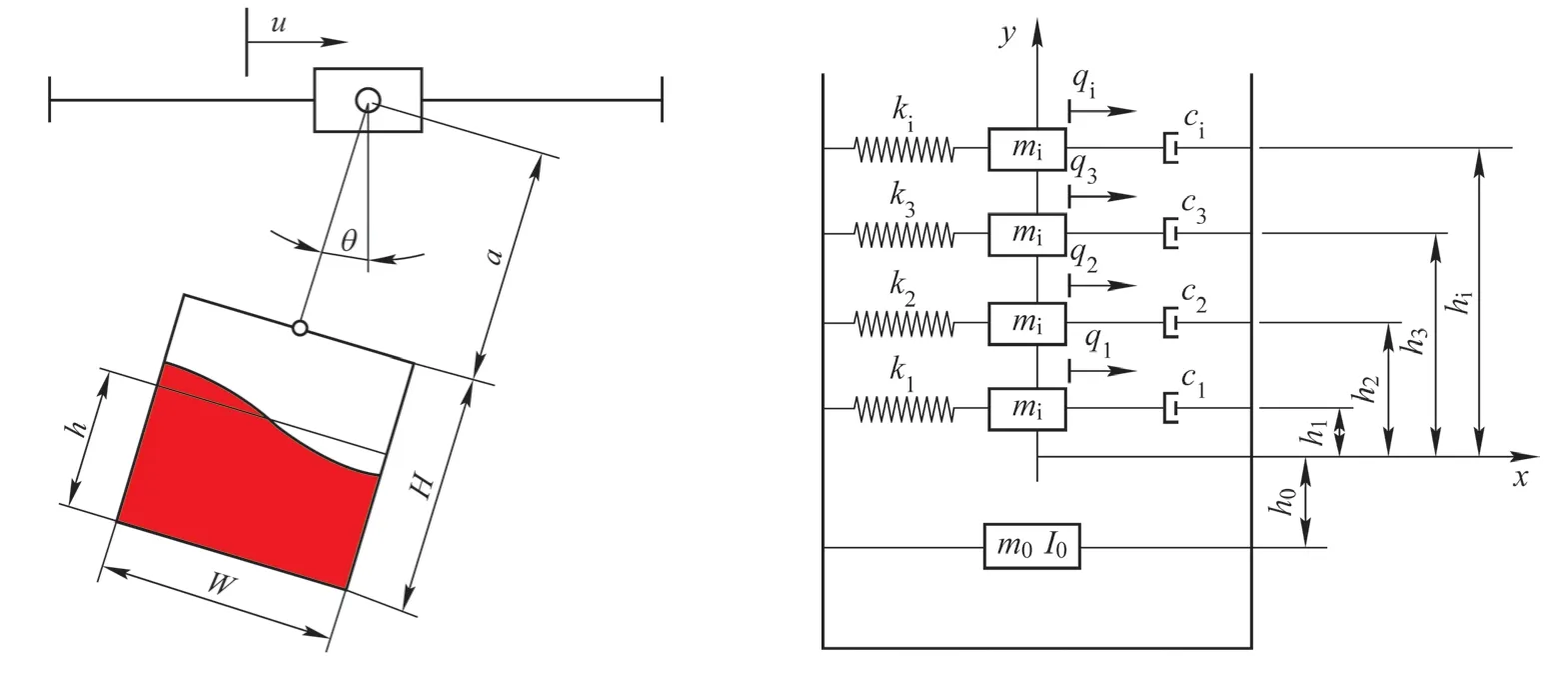
图1 吊运钢包系统等效力学模型

钢包通过长度为a的钢丝绳连接到小车上，小车在水平方向以加速度u‥(t)移动，而钢包在xy平面以摆动角θ摆动。每个质量块mi沿钢包横轴移动，相对于钢包具有相对位移qi(t)；每个qi(t)代表对应于第i阶晃动模态的广义位移。定义容器质心、液体固定质量m0和第i个点质量块mi的位置向量，对时间取导数得到速度向量，进而得到容器的动能、势能，并根据拉格朗日方程得到全耦合非线性微分方程

式中：lc、l0、li分别为小车到钢包质心、液体固定质量m0和第i个集中质量mi的距离，g为重力加速度，ζ、ωi分别为钢水晃动阻尼比和钢水晃动的i阶（i＝1，2，…，n）晃动模态频率。

由等效模型与横向激励下的解析解的力和力矩的等效、自然频率等效可以求得等效模型参数[4]，即有

在式（2）、式（3）中，ζ1n为Bessel 第1 类函数一阶导数的根，由低到高排列，对应晃动频率的特征值ξ11～ξ15为1.841 2、5.331 4、8.536 3、11.706、14.863。质量块的高度根据质量矩守恒方程：，其中h0为固定质量到钢水质心高度h/2 的距离；mf为钢包内钢水质量，mf=ρπR2h，晃动阻尼比ζ可表示为

式中：v=μ/ρ为钢水的运动粘度，ρ为钢水的密度，μ为钢水的动力粘度。

系统对于小车的等效转动惯量为

负载对小车的等效力矩为

钢水相对于其质心的转动惯量为[3]

若钢包吊运系统由静止开始吊运，则微分方程满足初始条件为

式中：θ0、0为钢丝绳的初始摆角和初始摆动速度，qi，0、i，0为质量块质量mi相对于钢包壁的初始位移和速度。

考虑到钢水包在实际工况中以静止开始搬运，故运动方程中的初始条件设为零初始条件。通过假设较小的振荡角θ和较小的表面波振荡qi来线性化，可将式（1）简化为

等效模型中钢水自由液面在钢包内壁处的高度为[4]

式中：δ(t)为钢包内壁液位高度变化，用来表征等效模型中钢水晃动程度。

为了尽可能地符合生产实际要求，模型参数选取了一组具有代表性的参数，钢水动力粘度系数随其温度、各元素含量等影响，查阅相关文献[5]设置0.02 Pa·s，系统模型详细参数如表1 所示。

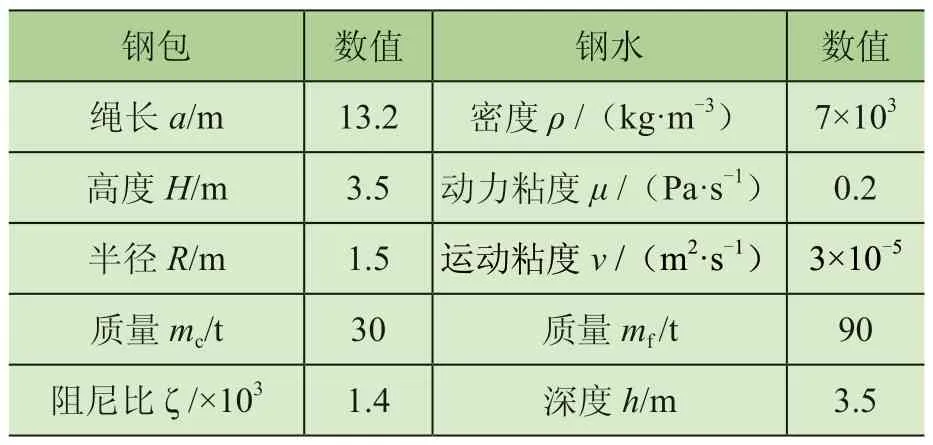
表1 钢包吊运系统参数

2 系统特性分析

钢水晃动主要集中在晃第一阶反对称模态[6]，为了使得模型更简洁，控制器的设计仅考虑第一阶反对称模态，然后将模型线性化得到

令x1＝θ，x2＝θ，x3＝q1，x4＝q1，得到状态空间方程并化成标准形式。为了分析桥式起重机系统模型的稳定性、能控性、能观性，将表1 参数带入到上述状态方程中，即有

由以上关系解得其特征根为eigA＝[0.807 8i-0.807 8i-0.005+3.528 5i-0.005-3.528 5i]T，特征值均未出现在虚轴的右平面，该系统为临界稳定性。从物理意义讨论，式（6）的模型系统忽略了空气阻尼等非必要干扰，但因现实工况下存在抑制阻尼，摆幅会逐渐减小，最终吊重的摆动会衰减为零，使钢包吊运系统达到稳定状态。

矩阵A、矩阵C可以评估可观测性，可观测性判据是可观测矩阵为满秩，可表示为

将系数矩阵A和矩阵C代入式（8） 即有：rankQO=4，由可观测性判据可认为该系统是可观的。常系数矩阵A及常系数矩阵B可以评估可控制性，这2个矩阵组成的可控性矩阵为满秩，可表示为

把系数矩阵A和矩阵B带入式（9） 即有：rankQc=4，根据可控性判据可认为系统是可控的。

3 光滑整形控制介绍

输入整形算法是将小车的控制信号经过整形后输入到系统中，从而消除摇摆。利用滑车的速度变化控制摆角大小是一种前馈控制方法，广泛应用于起重机防摇摆。在当前电子防摇中，大多需要安装吊重摆角传感器，成本较高，而在输入整形算法控制中无需实时测量吊重的摆角，可以大幅节约成本[7]。虽然输入整形控制为开环控制，受风力等外界因素的影响较大，而吊运钢包的吊运钢包的起重机位于室内厂房，故采用该算法的经济性非常高。光滑整形算法原理如图2 所示。

图2 输入整形算法原理图

首先确定幅值，以保证增益在整形前后的幅值相同，设定整形控制器脉冲幅值之和为1，。为了使系统不发生超调现象，整形控制器脉冲幅值应全部为正数，则Ai＞0。为了提高系统响应速度，最大程度地减小延迟时间，则t1=0；而实际上，输入整形控制器延迟脉冲的延迟时间应全部为正数，则ti＞0。

加入输入整形控制器，系统对单位脉冲响应为

将式（10）进行三角级数展开然后变形可得

其中

式中：ωn为固有频率，ξ为系统阻尼比，ωd为阻尼振荡频率。

对式(10)和式(11)进行比较，即可得到残留振荡为

对于墨西哥而言，发展竹建筑的意义不仅仅是出于经济方面的考虑，还可以缓解5个世纪以来土著群体所受的社会压迫。墨西哥土著居民尽管被殖民化，但他们的传统仍然存在，而且他们的生产潜力也仍然存在。正如墨西哥谚语所说“他们试图埋葬我们，但他们不知道我们是种子”。

为了抑制振荡，只要令C（ωn，ξ）、C（ωn，ξ）关于ωn的各阶导数等于零，然后联立、t1=0 即可得到光滑整形控制器的脉冲幅值Ai和延时ti为

其中

式中：T为系统振动周期。

通过以上计算，分别求得整形器的幅值和延时即可设计光滑整形器，然后利用Simulink 建立级联光滑整形器仿真，如图3 所示。

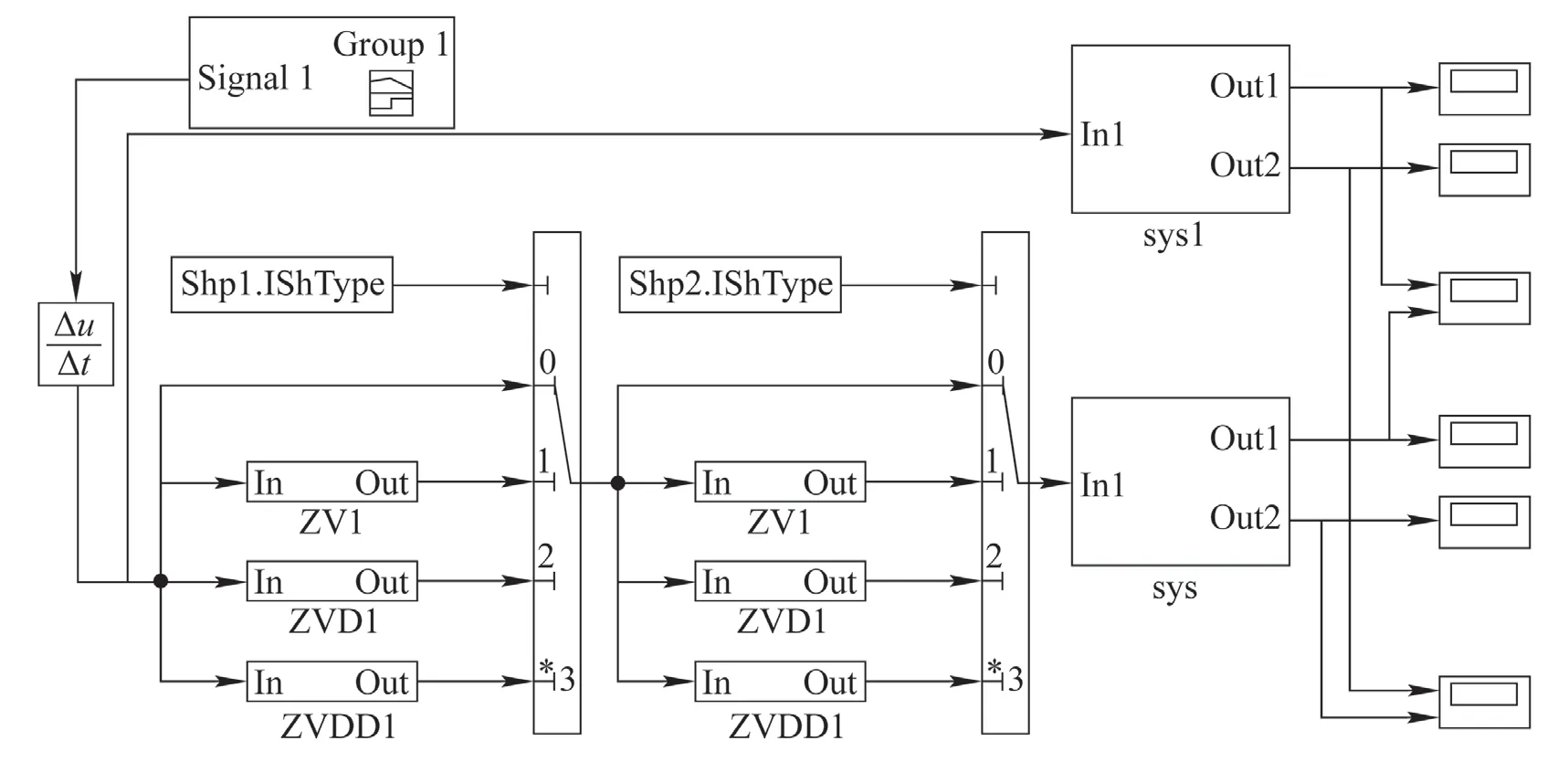
图3 级联光滑整形器Simulink 仿真图

4 算例研究

为了探索钢包吊运系统在极限工况时的系统响应，分析不同光滑整形器的控制效果，本文采用较大加速度曲线对系统施加驱动，在表1 所示系统参数及外部激励作用下，采用3 种整形控制器分别对钢包吊运系统进行振荡抑制，这3 种整形控制器的效果如图4 ～图8 所示。

图4 加速度曲线图

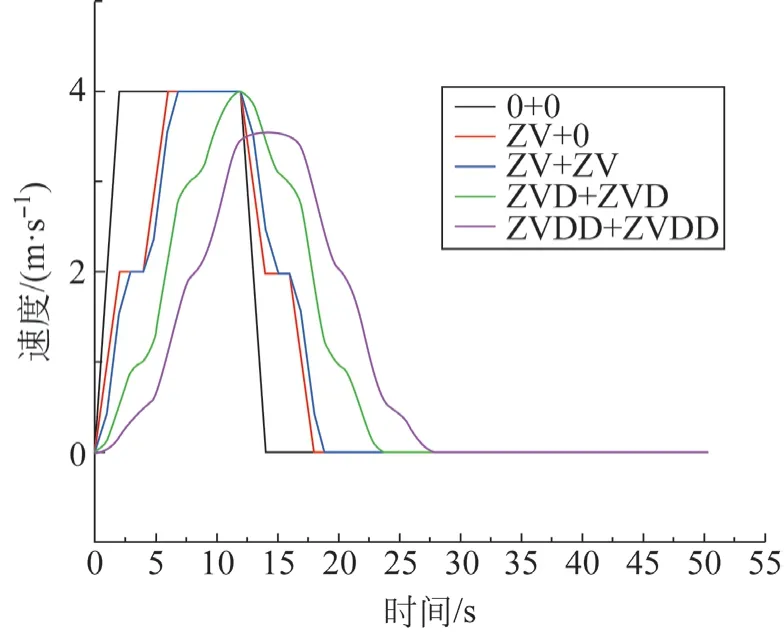
图5 速度曲线图

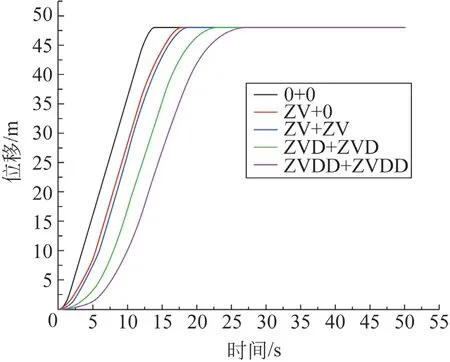
图6 小车位移曲线图

图7 钢丝绳摆角图

图8 钢水晃动响应

由图4 可知，在加入ZV 整形控制器后，系统的输入加速度幅值减半，但整个驱动过程相比于原加速曲线延时了约4 s；在加入双ZV 级联整形控制器后，加速度曲线进一步平滑，但其加速度延时相比于ZV 整形控制器基本不变；当加入双ZVD 级联整形控制器后，加速度曲线进一步平滑，但加速度曲线延时至23 s 附近；当加入双ZVDD 级联整形控制器后，加速度曲线幅值进一步降低，变得更加平滑，但稳定时间延时至29 s 附近。

由图5 可知，当加入ZV 整形控制器后，小车速度曲线的斜率有降低，匀速运行时间减小，且小车停止时间增加了约4 s；当加入双ZV 级联整形控制器后，小车的速度曲线斜率和小车停止的时间基本不变；当加入双ZVD 级联整形控制器后，小车速度曲线斜率继续降低，且小车匀速运行时间几乎减小到零，小车停止时间延时至23 s 附近；当加入双ZVDD 级联整形控制器后，小车的最大速度有所减小，小车停止的时间增加至28 s附近。

由图6 可知，从小车的位移曲线可以看到5 种方案都能将小车送达指定位置，但相比于未整形方案加入整形控制器后，到达指定位置的时间有所延长，且引入的整形控制器越复杂，则小车到达指定位置的时间越长。

由图7 可知，未加入整形控制器的钢丝绳摆角非常大，在极限加速度驱动下，钢丝绳最大摆角达到了30°以上，这对起重机特别是钢水包吊运来说非常危险。然而，在加入整形控制器后，钢丝绳摆角得到较大改观。当加入ZV 整形控制器后，钢丝绳的最大摆角降到8.5°左右，在17.5 s 以后摆角下降至2°以内；当加入双ZV 级联整形控制器后，钢丝绳白响应与ZV 整形控制器结果基本一致；当加入双ZVD 级联整形控制器后，钢丝绳最大摆角下降到5°以内，且在22 s 以后下降到1°以内；当加入双ZVDD 级联整形控制器后，钢丝绳的最大摆角下降到4°以内，且在25 s 以后基本做到了0 振荡。

由图8 可知，未加入整形控制器的钢水最大晃动达到12 cm，这对钢水运输来说非常危险。在加入ZV整形控制器后，晃动的最大的幅值下降至5 cm，在18 s 后残余晃动幅值也能保持在3 cm 以内；当加入双ZV 级联整形控制器后，钢水晃动的最大幅值下降至2 cm 左右，在20 s 后钢水晃动基本为零震荡；在加入双ZVD 及ZVDD 级联整形控制器后，钢水晃动的幅值进一步减小，分别达到1 cm 和0.5 cm，且在25 s 后使钢水晃动为零震荡。

5 结论

钢包吊运系统的定位防摆在重型铸造行业具有非常重要的意义，由于我国大多依据工人经验手动消摆，精度差稳定性低。为此，根据铸造起重机吊运钢水的特殊作业状态，建立吊运系统等效力学模型，通过建立钢包吊运系统的质量－弹簧－阻尼模型推导出运动方程。采用双级联光滑整形器对钢包吊运系统进行安全快速精准定位控制。结果表明：光滑整形器不仅可以消除小车停止后钢丝绳残余摆角和钢水晃动，还能保证整个吊运过程中钢丝绳摆角和钢水晃动始终保持较低水平。采用更复杂的光滑整形控制器控制效果会更好，但计算成本及系统稳定的时间将会增加。在实际工程应用当中，出于经济上的考虑，在满足控制目标的前提下，应当尽可能地降低整形控制器复杂度。