基于拉普拉斯变换法的简支梁桥振动频率研究

高彦鑫，仝瑞金

（1.天津市政工程设计研究总院有限公司南沙分公司，广东广州 510000）2.广州南沙交通投资集团有限公司，广东广州 510000）

0 引言

结构振动频率是动力特性的重要指标，反映了结构的整体刚度、组成体系和质量分布等。在桥梁竣工或者运营阶段，通常需要对结构进行持续监测，获得其振动频率。如果实测值大于理论计算值，说明桥梁结构的实际刚度较大，反之则说明桥梁结构的刚度偏小，可能存在开裂或其他不正常现象。因此，准确测量桥梁结构的振动频率至关重要。对于刚度较大的桥梁，如简支梁桥，自然激励通常较难获得准确的振动频率，通常需要进行跑车或者跳车试验，对桥施加激振荷载，才能较准确地获得其振动频率。但由于车辆的存在，车辆和桥梁组成了车-桥耦合系统，因此在动力试验中，得到的桥梁振动频率实际上是以桥梁振动为主要振动形式的车-桥耦合系统的振动频率，而非桥梁自身的固有频率，工程上常把车-桥耦合系统的桥梁振动频率称为桥梁有载频率[1]。在动载试验中，如果忽略车辆质量的影响，通常会造成频谱分析时的波峰漂移，从而难以判定桥梁的真实频率及阶次，如图1 所示。

图1 频谱分析时的波峰滑移

早在1997 年，Charles R Farrar 等[2]和2003 年Chul-Young Kim[3]通过桥梁动载试验，发现桥梁有载频率与固有频率误差较大的现象，揭示了车辆位置对桥梁频率的影响。应怀樵[4]利用传递矩阵分析得到了移动荷载在简支梁不同位置处的各阶频率变化曲线，表明了移动荷载的位置和大小对系统的各阶频率有很大的影响。唐贺强[5]根据桥梁固有频率的定义求解桥梁振动微分方程，给出了列车荷载作用下简支梁桥有载频率的解析表达式。程永春等人[6]利用模态分析对车桥系统方程解耦得到多个车辆作用下桥梁的有载频率。

桥梁有载频率与固有频率不仅在车桥耦合系统中误差较大，在人行桥耦合振动方面同样如此。因此，研究桥上移动荷载对桥梁振动频率的影响十分必要。本文利用拉普拉斯变换[7]，通过多点叠加的方法，分析车重在不同位置时的简支梁桥振动频率，为理论计算及测量分析提供理论依据。

1 振动频率计算理论

结构振动频率是结构动力分析与控制的重要参数，我国规范中将冲击系数定义为桥梁基频的函数，因此结构振动频率的求解有重要的意义。结构振动频率的求解主要有试验法[8]、数值法[9]和解析法[10-11]。试验法一般是利用加速度传感器测量加速度时程数据，然后通过频谱分析获得响应的振动频率。数值法主要是建立有限元模型，对结构进行动力分析，得出振动频率及相应的振型。解析法则通过显式求解振动方程获得频率公式，有效地避免了试验法和数值建模的繁琐，具有简单、高效和准确等优点，一直以来都是研究人员关注的重点。为了分析车重在不同位置时的简支梁桥振动频率，本文的理论模型如图2 所示，车轴重Mi位于xi处，同时不考虑轴力N的影响。

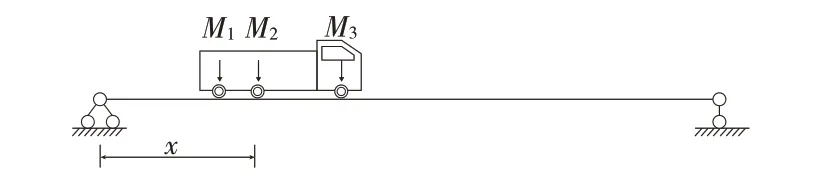
图2 理论模型图

已知欧拉梁的横向振动方程[12]如式（1）：

式中：ρ为密度，kg/m3；A为横截面面积，m2；I为截面惯性矩，m4；E为弹性模量，N/m2；u为梁的横向位移，m；P为外加荷载，N。

质量M可以看成是作用在梁上的外荷载，即外荷载为Mδ(x-xi)∂2u(x,t)/∂t2，由于车辆荷载的车轮数不同，外力增加的个数与位置也会不同，得到图2 中简支梁的横向振动方程为：

式中：R为施加外力的个数。

利用Laplace 变换的微分性质：

对式（4）做Laplace 变换并化简后可得象函数如式（6）：

通过查表法对式（6）进行Laplace 反变换：

解方程s4-k4= 0，得s1=k，s2= -k，s3=ik，s4= -ik，无重根。

因为Y( 0 )= 0，Y''( 0 )= 0，可得Y(x)和Y''(x)表达式如式（7）：

对式（7）进行二次求导：

l处的位移与弯矩表达如式（9）、式（10）：

式中：

又由于Y(l)= 0，Y''(l)= 0，所以求行列式得特征方程如式（11）所示：

由式（11）可求出非零k值，最终激振荷载位于任意位置下简支梁桥的各阶振动频率可由式（12）求出：

2 算例

以某简支梁桥为例，利用本文理论计算方法和有限元方法[13-14]进行对比验证。有限元模型如图3 所示，桥长为30 m，桥宽4.8 m，梁高1.9 m，容重为25 kN/m3，横截面积A为2.58 m2，弹性模量E为3.25×1010N/m2，截面惯性矩I为1.226 606 m4，无荷载作用下的利用有限元计算基频为4.297 Hz，采用规范方法计算所得的基频则为4.337 Hz。现有一辆三轴加载车，其质量约为14.5 t，其轴间距如图4 所示，前轴重40.635 kN，中后两轴重相等，为52.245 kN。

图3 单箱单室简支梁桥有限元模型

图4 试验车平面尺寸（单位：m）

通过有限单元法软件Midas Civil 模拟全车通过桥梁时的频率变化情况，与本文的理论计算结果进行对比。计算结果如表1 所示（以车辆中轴位置为准）。

表1 频率对比

对应的加载位置与频率的关系如图5 所示。

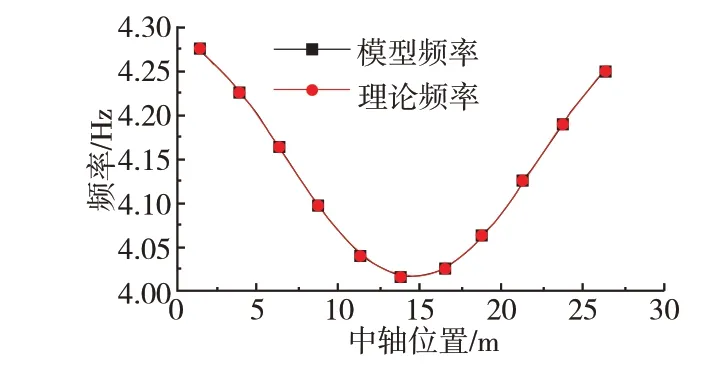
图5 频率对比图

跨中有载频率与桥梁固有频率降低值计算如式（13）：

结果表明，车辆移动过程中，桥梁振动频率呈现从跨中向支座两端逐渐增大的规律。车辆荷载行驶到桥梁跨中时，桥梁自振频率降低了6.47%，车重对简支梁振动频率的影响不可忽略。本文推导的公式的计算结果与模型计算结果基本一致，证明该理论解的正确性。

3 结论

在桥梁的动载试验中，对于刚度较大的桥型通常需要使用激励法获得其振动频率，而跑车和跳车试验是主要的激励方式。本文利用拉普拉斯变换，通过多点叠加的方法，考虑激励源质量并获得了行车质量在不同位置下简支梁振动频率的理论解。主要结论如下：

a）车重对简支梁振动频率的影响不可忽略，车辆移动过程中，桥梁振动频率从跨中向支座两端逐渐增大。

b）车辆重量越大，有载振动频率的变化范围越大；桥跨越长，有载振动频率的变化范围越大；桥梁质量越大，有载振动频率的变化范围越小。

c）利用本文方法，可以准确获得振动过程的频率上下限，得到有载振动频率峰值滑移的范围，从而准确确定振动频率阶次。