考虑弦杆约束的新型板桁加劲梁扭转变形计算方法

王路，侯文崎，张哲滔，张晓勇，温伟斌

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. 山东高速工程检测有限公司，山东 济南，250000；3. 中南大学 力学教学实验中心，湖南 长沙，410083；4. 中铁大桥勘测设计院集团有限公司，湖北 武汉，430056)

随着高速铁路建造技术的发展，京沪高铁沪通长江大桥[1-2]、连镇铁路五峰山长江大桥[3]、荆岳铁路洞庭湖大桥[4-5]等千米级跨度的铁路桥梁相继建成。千米级跨度铁路桥梁设计关键在于结构合理刚度取值，加劲梁刚度是重要控制指标之一。目前，加劲梁竖向刚度和横向刚度均已有较明确的规定限值，但扭转刚度尚无明确控制指标和规定限值[6-8]。受车辆偏载和横向风荷载作用，加劲梁存在扭转变形，会引起同一轨道横截面上两侧钢轨高差，直接影响到列车运行的安全性和旅客乘坐的舒适性[8-9]。李迎九等[7-8]提出加劲梁扭转变形限值可参考高速铁路轨道水平几何状态幅值评价允许偏差验收值，即梁体扭转角度为2.0‰ rad，同一截面轨道横断面高差不大于1.5 mm。但对于板桁加劲梁扭转刚度设计，上述参考值缺乏理论指导意义和可操作性。因此，亟待对千米级跨度铁路桥梁加劲梁扭转变形及其影响因素进行研究。公铁合建模式的板桁加劲梁由于桁高大、桥面宽、竖向刚度和横向刚度大，成为千米级跨度铁路桥梁首选加劲梁型[7-8]。板桁加劲梁由钢桁梁和正交异性钢桥面板组成，通常下层桥面系设置有横梁，上层桥面系设置有上横联，以将桥面荷载横向传递至钢主桁。但考虑车辆限界要求，往往主桁桁高较大。为更充分利用主桁截面空间，近年来出现取消上横联、采用多横梁式正交异性整体钢桥面的新型板桁加劲梁，如拟建的李埠河公铁两用悬索桥(主跨1 090 m)和江阴悬索斜拉长江大桥(主跨1 780 m)。相比于传统板桁加劲梁，新型板桁加劲梁竖向刚度和横向刚度变化不大，但扭转刚度控制问题更加突出。板桁加劲梁扭转变形复杂，影响因素较多[10-13]，不同理论或方法所得结果差异较大。目前，板桁加劲梁扭转变形分析方法主要有离散模型分析法和连续模型分析法。离散模型分析法如板梁组合单元法[14-17]、等效空间梁单元法[18-19]和板桁结构精细化有限元法[20]是考虑钢主桁与正交异性钢桥面板的组合作用，将板桁加劲梁离散为各种空间单元力学行为进行分析。离散模型分析法的计算结果较精确，但建模精度要求高，尤其应用于大跨板桁组合体系桥梁时，单元数量多，计算效率较低。连续模型分析方法是将实际为空间杆系结构的钢桁梁等效为闭口薄壁箱梁，再依据薄壁箱梁扭转理论分析其扭转变形。该方法最早应用于钢桁梁扭转分析，通过与模型试验结果对比，计算精度已得到验证[21]。相比于离散模型分析法，连续模型分析法的单元数量少，计算效率大幅提高，更适于板桁加劲梁扭转变形计算方法及影响因素研究。

基于薄壁箱梁自由扭转理论，有研究者采用连续模型法，提出了板桁加劲梁扭转惯性矩质量、扭转惯性矩简化计算公式及连续化等效模型，并应用于大跨度悬索桥扭转变形分析[22-24]。但薄壁箱梁扭转研究表明[13,25-26]，箱梁梗腋处对应板桁加劲梁的主桁弦杆，对加劲梁扭转变形的约束作用不可忽略[27]。上述基于自由扭转理论的板桁加劲梁扭转刚度研究未考虑主桁弦杆、桥面系等构件的约束作用，计算精度较低。基于乌曼斯基约束扭转理论，彭旺虎[28]通过参数形式统一的钢桁架和正交异性钢桥面板的等效厚度建立了板桁加劲梁连续化等效薄壁梁模型，刘凯园[11]建立了板桁加劲梁横截面刚性扭转和剪切变形微分方程组。这些模型和计算方法虽然精度有所提高，但计算公式和计算过程复杂。为此，本文以某拟建千米级跨度铁路桥梁为背景，基于约束扭转理论构建新型板桁加劲梁连续化等效模型，考虑弦杆对加劲梁扭转变形的纵向约束作用，提出加劲梁扭转变形计算方法，以便为千米级跨度铁路桥梁扭转刚度研究提供参考。

1 新型板桁梁构造

某拟建千米级跨度高速铁路悬索桥，跨度布置为(122+1 090+120+92) m，主梁采用公铁合建模式的新型板桁加劲梁，节间长度a为16 m，主桁高h为12 m，桥面宽度b为38 m。图1 所示为该桥结构示意图，图2 所示为新型板桁加劲梁构造示意图。相比于传统板桁加劲梁[3]，新型板桁加劲梁主桁桁高由16 m 优化至12 m，桁内空间利用更充分，钢材用量也大大节省。图2中，主桁上弦杆和下弦杆均为箱型截面，内设板式加劲肋；竖杆和斜腹杆均为工字型截面，在腹板中间设有沿杆件长度方向的加劲肋；桥面系则为由倒T形横梁、U形加劲肋和钢桥面板共同组成正交异性钢桥面，其中，下层桥面系还有小纵梁。表1所示为该桥各主要组成部分材料参数。

图1 悬索桥结构示意图Fig. 1 Structural diagram of suspension bridge

图2 新型板桁加劲梁构造示意图Fig. 2 Structural diagrams of new plate truss stiffening girder

表1 新型板桁加劲梁悬索桥主要构件材料参数Table 1 Material parameters of main components of suspension bridge with new plate truss stiffening girder

2 连续化等效模型的构建

2.1 连续化等效方法

板桁加劲梁连续化等效的目的是将主桁腹杆、U 肋、纵梁、横梁等效为连续薄板，与主桁弦杆、钢桥面板共同形成闭口薄壁箱形梁。等效原则为：在相同扭矩T作用下，等效闭口薄壁箱梁的扭转变形θ与板桁加劲梁的扭转变形θ'相同，即扭转变形示意图(图3)中的θ=θ'。需要指出的是，在主桁的等效中，假设弦杆其他变形与弯曲变形相比，对主桁等效的贡献很小，可以忽略不计。在扭矩T作用下，板桁加劲梁的上层桥面系、主桁和等效闭口薄壁箱梁的顶板、腹板受力变形状态如图4 所示。图4中，扭矩T可等效为2对力偶V·b和H·h，则桥面系或主桁受横向力H或竖向力V作用。桥面系或主桁的剪切变形等效原则为：在相同H或V作用下，对于等效闭口薄壁箱梁的顶(底)板和腹板的剪切变形(γ′q和γ′z)与板桁加劲梁的桥面系和主桁的剪切变形(γq和γz)，有γq=γ′q，γz=γ′z。

图3 扭转变形等效示意图Fig. 3 Diagrams of equivalent torsional deformation

图4 受力变形状态等效示意图Fig. 4 Diagrams of equivalent stress and deformation state

2.2 主桁等效厚度

主桁由竖杆、斜腹杆和弦杆组成，弦杆仅考虑抗弯刚度对主桁剪切变形的贡献。依据剪切变形等效原则[32]，主桁等效厚度tz为

式中：Af为斜腹杆面积；d为斜腹杆长度；Isx和Ixx分别为上、下弦杆面内惯性矩。

2.3 桥面系等效厚度

桥面系等效厚度包括3部分：1) 正交异性钢桥面板，等效厚度记为t′；2) 主桁上弦杆和横梁组成上层桥面框架，等效厚度记为3) 主桁下弦杆、横梁和小纵梁组成下层桥面框架，等效厚度记为此处，弦杆仅考虑面外弯曲刚度，则上层桥面系等效厚度为下层桥面系等效厚度为

2.3.1 正交异性钢桥面板

正交异性钢桥面板由钢桥面板和U 肋组成，如图5(a)所示。图中，tu为U 肋板厚，tm为桥面板板厚，Lu为U肋上口宽度，Lm为相邻U肋净间距，Lus为U 肋周长。在横向剪力作用下，正交异性钢桥面板上剪力流可分为3 部分：1)qm，对应Lm范围内钢桥面板上的剪力流；2)qum，对应Lu范围内钢桥面板上的剪力流；3)qu，对应沿U 肋周长Lus分布的剪力流。为简便计算，将U 肋简化为如图5(b)所示倒梯形，其中，β为简化U 肋上肢倾角，Lus1为单上肢长，Lus2为底边长。

图5 正交异性钢桥面板剪力流示意图Fig. 5 Diagrams of shear flow of orthotropic steel deck

沿顺桥向取dz长度正交异性钢桥面板微段，如图5(c)所示。由qum引起的Lu范围内钢桥面板的剪应变γum和剪切变形Δum分别为

由qu引起U 肋单侧上肢的剪应变γs1和剪切变形Δs1分别为

如图5(d)所示，qu引起U肋的剪切变形Δus为

根据U 肋与Lm范围内钢桥面板的剪力平衡和变形协调条件，有qm=qu+qum，Δum=Δus，据式(2)和式(4)得

根据剪切变形等效原则，U 肋与Lu范围内钢桥面板的等效厚度t′u为

进一步考虑Lm范围内钢桥面板与的剪切刚度等效，得正交异性钢桥面板等效厚度tqu为

2.3.2 桥面框架

取1 个节间的上层桥面框架为隔离体，如图6(a)所示。该多层框架在节点横梁处受横向剪力H作用，将其分解为若干单层框架，每个单层框架受力状态如图6(b)所示。相比上层桥面框架，下层桥面框架增加了小纵梁，见图6(d)和图6(e)。

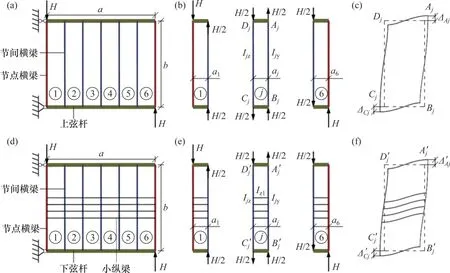
图6 桥面框架等效厚度计算示意图Fig. 6 Calculation diagrams of equivalent thickness of deck frame

将上层桥面框架中第j(j=1～6)号单层框架的右上、右下、左下、左上角点分别命名为Aj、Bj、Cj、Dj。在H作用下，上层桥面框架中第j(j=1～6)号单层框架变形如图6(c)所示，Aj和Cj这2 点相对各自原始位置的侧移ΔAj和ΔCj分别为

式中：Isy为上弦杆面外惯性矩；Ijz和Ijy分别为第j号单层框架两侧横梁的抗弯惯性矩，可取节间(点)横梁面外惯性矩的一半，即。

第j号单层框架中Aj和Cj这2点的相对侧移为Δj=ΔAj+ΔCj。将全部单层框架的相对侧移相加得到桥面系框架的总相对侧移，即。等效厚度为

在H作用下，下层桥面框架中第j号单层框架变形如图6(f)所示。当两点发生相对侧移时，4根小纵梁所受剪力为

式中：Izl为小纵梁的面外惯性矩。

根据式(8)，下弦杆和节点(间)横梁组成的框架所受剪力为

式中：Ixy为下弦杆面外惯性矩。

由H=H1+H2得

据式(9)，同理可求得下层桥面框架等效厚度t2″。

2.4 连续化等效模型

按照上述方法，可将新型板桁加劲梁等效闭口薄壁箱梁并约定x＞0和x＜0的上弦杆分别为1、2号弦杆，x＜0和x＞0的下弦杆为3、4号弦杆，等效模型示意图如图7 所示。图7 中，A1、A2、A3、A4分别为1、2、3、4号弦杆的面积，t1、t3分别为闭口薄壁箱梁顶、底板厚度，t2、t4分别为闭口薄壁箱梁左、右腹板厚度。

图7 新型板桁加劲梁连续化等效模型示意图Fig. 7 Schematic diagram of continuous equivalent model of new plate truss stiffening girder

3 扭转变形计算方法

3.1 基本假定

基于上述连续化等效闭口薄壁箱梁，进行如下假定：

1) 箱梁截面符合符拉索夫刚性周边假定，即截面形状不发生改变。

2) 忽略新型板桁加劲梁扭转变形中横截面桁内竖杆的影响。

3) 考虑主桁弦杆轴向刚度对等效闭口薄壁箱梁纵向翘曲的约束作用。

4) 材料采用线弹性本构模型。

3.2 截面扭矩

取长度为dz的等效闭口薄壁箱梁微段为隔离体，如图8所示。图8中，Tk为微段横截面上的扭矩，σ1、σ2、σ3、σ4分别为1、2、3、4号弦杆轴向应力；N1、N2、N3、N4分别为1、2、3、4 号弦杆轴力，q1、q2、q3、q4分别为在扭矩Tk作用下，等效闭口薄壁箱梁顶板、左腹板、底板、右腹板上剪力流。图9所示为等效闭口薄壁箱梁微段各薄壁剪切变形示意图，其中，u、v、w分别为等效梁截面上任一点沿坐标轴x、y、z方向的位移。

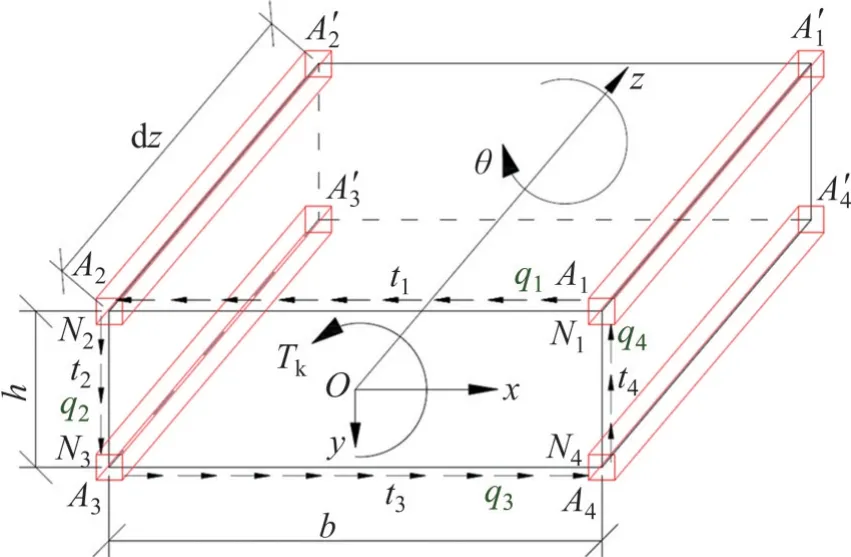
图8 等效闭口薄壁截面梁示意图Fig. 8 Diagram of equivalent thin walled beam

图9 薄壁剪切变形示意图Fig. 9 Diagrams of shear deformation of thin wall

根据各弦杆平衡条件，有

对于等效闭口薄壁箱梁，有q1=q2，q2=q4，则

3.3 几何方程

在扭矩Tk作用下，在图8所示等效闭口薄壁箱梁微段上任一截面绕z轴的扭转角为θ，有

记在扭矩Tk作用下，等效闭口薄壁箱梁微段顶板、左腹板、底板、右腹板的剪切变形分别为γ1、γ2、γ3、γ4，薄壁剪切变形示意图(图9)。根据剪切变形定义，可得

此即为等效闭口薄壁箱梁扭转变形几何方程。

3.4 扭转平衡微分方程

4 算例验证

4.1 算例设计

采用图2 所示新型板桁加劲梁，节间长度为16 m，考虑每跨分别设置1～4 个节间，设计4 个5跨连续梁算例，如图10 所示。新型板桁加劲梁各构件参数见表2。采用本文连续化等效方法，可将新型板桁加劲梁等效为图7所示闭口薄壁箱梁，等效壁厚见表3。

图10 4种算例示意图Fig. 10 Schematic diagrams of four example girders

表2 新型板桁加劲梁构件参数Table 2 Structural parameters of the members of new type of plate truss stiffening girder

表3 等效闭口薄壁箱梁壁厚Table 3 Wall thickness of equivalent closed thin-walled box girder

采用大型有限元软件Midas Civil 建立各算例的空间精细化有限元模型，其中，上弦杆、下弦杆、竖杆、斜腹杆、节点横梁、节间横梁、桁内竖杆、小纵梁均采用空间梁单元离散，正交异性钢桥面板采用板单元离散。单个节间共665个梁单元，876个板单元。图11所示为算例1的精细化空间有限元模型。

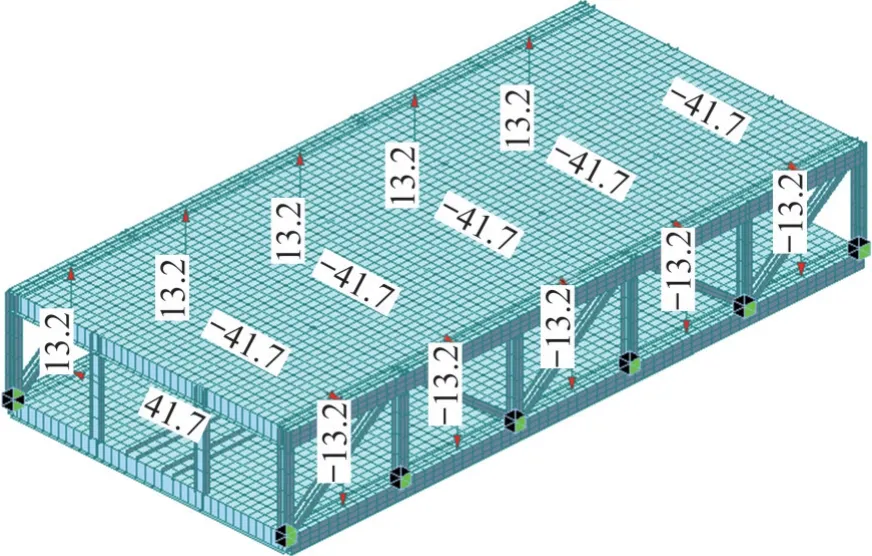
图11 算例1空间有限元模型Fig.11 Spatial finite element model of example 1

在各跨跨中截面4 个角点上施加扭矩T=1.0 MN·m，以1 对水平力偶和1 对竖向力偶实现，水平力偶为41.67 kN×12 m，竖向力偶为13.16 kN×38 m，如图11 所示。在该扭矩作用下，新型板桁加劲梁扭转角θ如图12所示。

图12 新型板桁加劲梁扭转角示意图Fig.12 Diagram of torsion angle of new plate truss girder

式中：Δy1和Δy2分别为角点A1和A2沿y向的位移。

4.2 计算结果对比分析

分别采用空间精细化有限元法、按照式(22)(考虑弦杆纵向约束)和式(23)(不考虑弦杆纵向约束)，计算上述4 个算例扭转角沿梁长分布，见图13。表4所示为不同算例跨中加载截面的扭转角计算结果。由图13和表4可见：

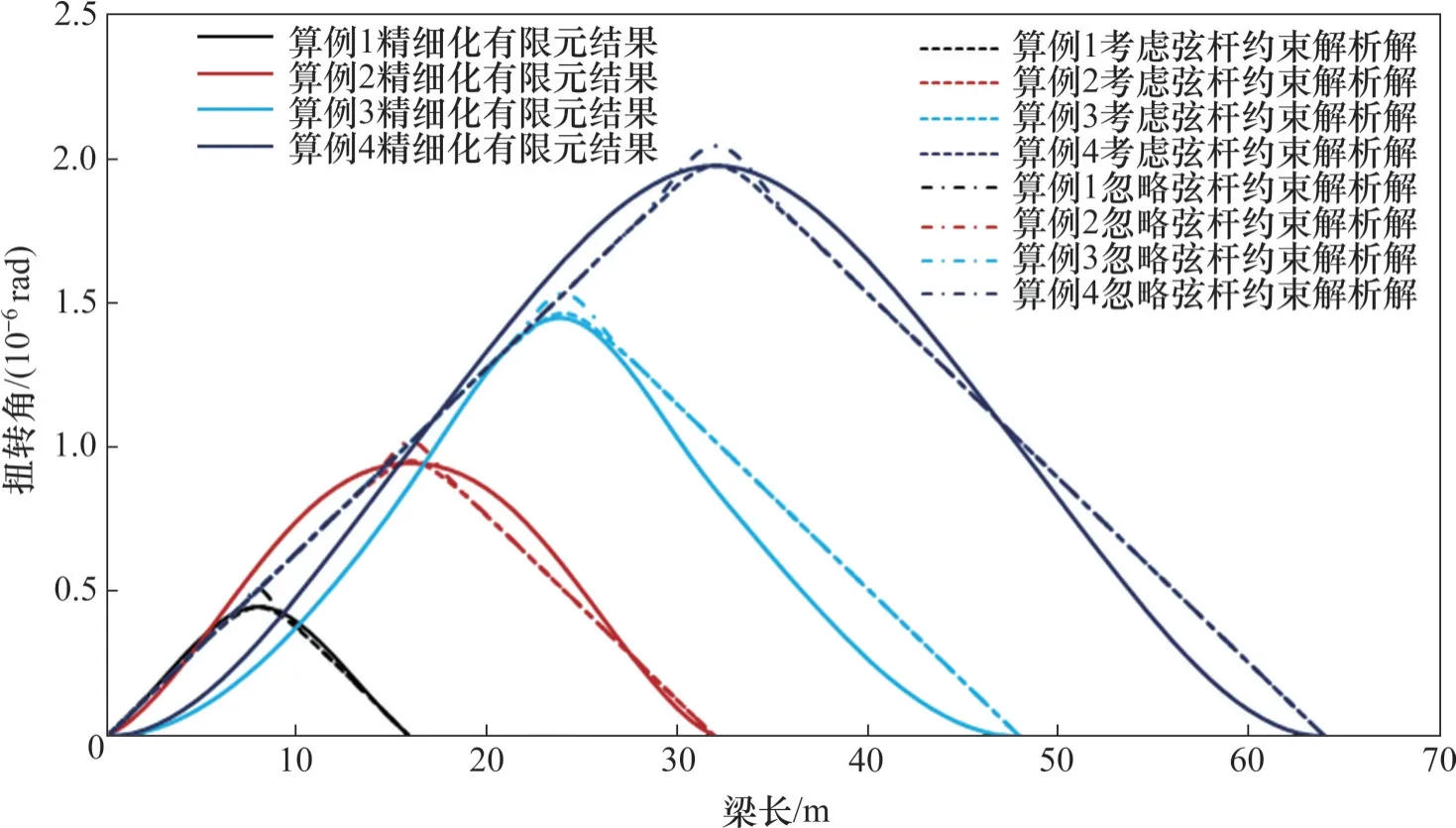
图13 不同方法计算所得扭转角沿梁长分布Fig. 13 Torsion angle of example girders obtained by different methods

表4 不同算例跨中加载截面扭转角Table 4 Torsion angle at the mid-span loading cross-section of example girders

1) 弦杆纵向约束对新型板桁加劲梁扭转变形的影响不可忽略。相比于空间精细化有限元计算结果，考虑弦杆纵向约束时，计算所得连续化等效模型扭转角的相对误差最大仅为1.2%；不考虑弦杆约束作用时，计算所得连续化等效模型扭转角的相对误差最小也有3.6%，最高达14.9%。

2) 随连续梁跨度增大，弦杆纵向约束对加劲梁扭转变形的影响逐渐减小。对比算例1 和算例4的连续化等效模型扭转角计算结果，当每跨主桁节间由1增加到4时，考虑弦杆纵向约束影响的扭转角由13.7%降至3.3%。

但是，需要指出的是，当新型板桁加劲梁应用于大跨度悬索桥时，主桁节点处的主缆吊索作用相当于加劲梁的弹性支撑，类似于本文算例1，弦杆纵向约束仍不可忽略。

5 新型板桁加劲梁悬索桥扭转变形分析

5.1 实桥空间有限元模型

图14所示为采用Midas civil建立的图1所示梁悬索桥的全桥空间精细化有限元模型，其中，主塔采用梁单元离散，主缆和吊索采用索单元离散，板桁加劲梁的上弦杆、下弦杆、竖杆、斜腹杆、节点横梁、节间横梁、桁内竖杆、小纵梁采用梁单元离散，正交异性钢桥面板采用板单元离散。全桥共12 662 个梁单元，5 420 个板单元，266 个索单元。

收获现值法主要运用了财务管理中计算现值的方法，通过预测林木到达主伐期的木材量，利用木材市场价格倒算出木材价值并折现，才扣除核算日到主伐期可能产生的各项支出的现值，剩余即为该核算对象的核算价值。其计算公式为：

图14 悬索桥空间精细化有限元模型示意图Fig. 14 Diagram of spatial refined finite element model of suspension bridge

图15 所示为扭转计算工况示意图。其中，下层桥面系布置单线铁路(ZK 活载)+两车道公路(Ⅰ级车道荷载)，上层桥面系布置四车道公路(Ⅰ级车道荷载)。计算时，每延米外扭矩mt=528.37 kN·m，按均布线荷载施加。

图15 扭转计算工况示意图Fig. 15 Schematic diagram of torsion condition calculation

5.2 等效单梁有限元模型

根据图7 和表3，采用Midas Civil 建立新型板桁加劲梁悬索桥等效单梁有限元模型，如图16 所示，新型板桁加劲梁等效参数见表5。表5 中，等效扭转惯性矩Izz按式(22)计算得到，其余参数按实际截面计算得到。主塔仍采用梁单元离散，主缆和吊索仍采用索单元离散。该等效单梁有限元模型共289 个梁单元，266 个索单元，单元数量相比图14 所示空间精细化有限元模型大幅度减少。扭转计算工况与图15 中相同，按偏心均布线荷载施加，荷载集度为p=52.837 kN/m，偏心距e=10 m。

表5 新型板桁加劲梁等效参数Table 5 Equivalent parameters of new plate truss stiffening girder

图16 等效单梁有限元模型Fig. 16 Finite element model of equivalent single girder

5.3 加劲梁扭转角解析解

当新型板桁加劲梁应用于悬索桥时，据文献[29]所得悬索桥闭口薄壁箱形加劲梁扭转变形计算方法，式(22)可修改为

式中：v为加劲梁竖向位移；为恒载状态下主缆线形；f为主缆垂度；L为主缆跨长；，为恒载引起的主缆拉力的水平分量；q为恒载集度；Hp为相应于竖向挠度v的活载主缆拉力；HL和HR分别为扭转位移引起的左、右主缆附加缆力，HL=-HR；Lc为缆索长度项，；Ec为主缆弹性模量；Ac为主缆的截面面积，2Ac1=Ac。

5.4 计算结果对比分析

分别采用上述空间精细化有限元模型、等效单梁模型、解析式(25)，所得悬索桥加劲梁主跨挠度和扭转角分别见图17 和图18，主缆缆力和吊索索力见图19和图20。由图17～20可见：

图17 不同方法计算所得悬索桥加劲梁挠度对比Fig.17 Deflection comparison of suspension stiffening girder obtained by different methods

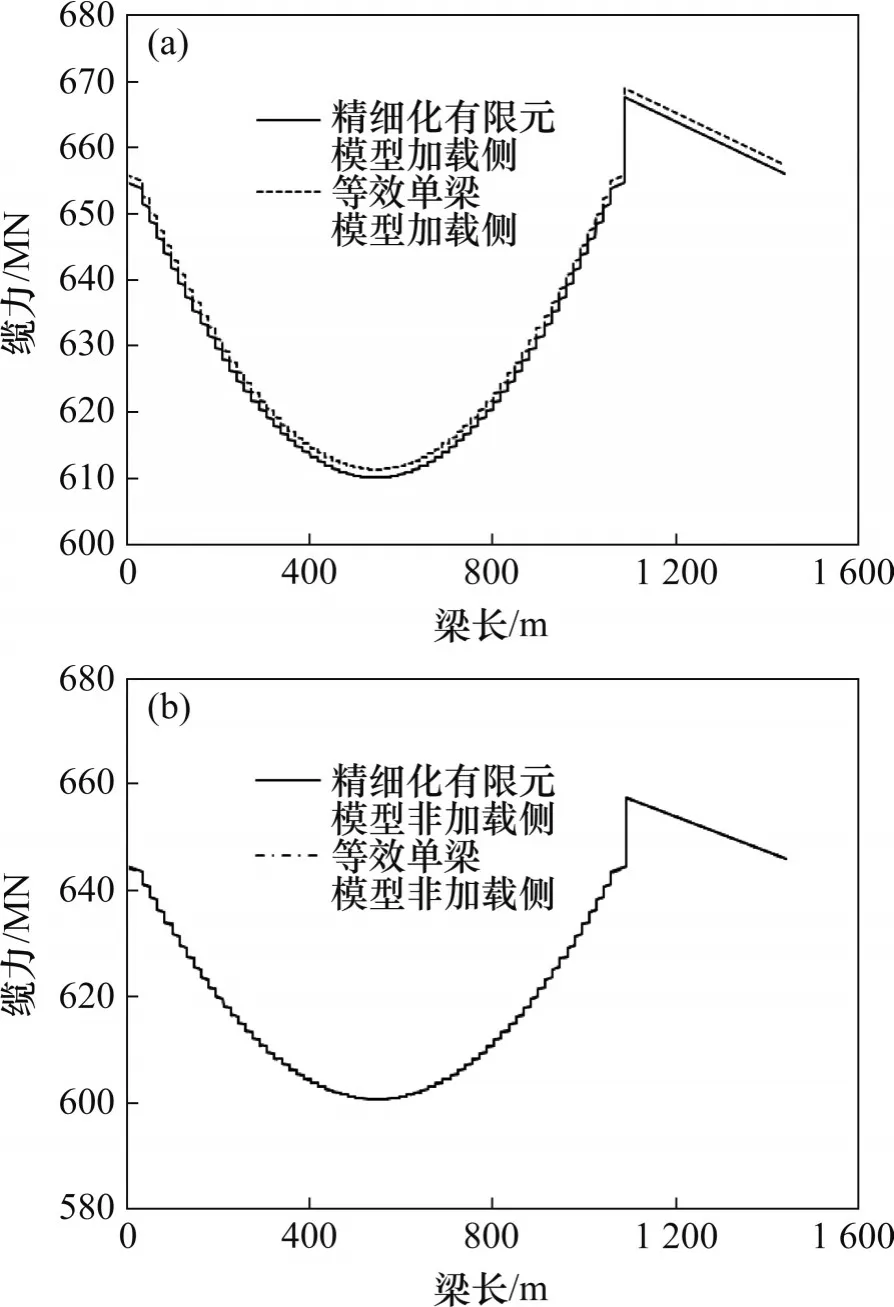
图19 不同方法计算所得加载侧和非加载侧主缆缆力对比Fig.19 Cable force comparison of the main cable of loading side and non-loading obtained by different methods

图20 不同方法计算所得加载侧和非加载侧吊索索力对比Fig. 20 Internal force comparison of the main cable of loading side and non-loading obtained by different method

1) 等效单梁模型与空间精细化有限元模型相比，加劲梁挠度和扭转角均偏大，2个模型计算结果之间的误差由主塔处向跨中逐渐增大。在主跨跨中，加劲梁挠度相对误差最大为1.8%，扭转角最大相对误差为14.7%，其原因是该等效单梁模型未考虑主桁截面畸变和纵向翘曲。但在悬索桥加劲梁刚度初步设计阶段，上述误差均在可接受范围内。

2) 等效单梁模型与空间精细化有限元模型相比，加劲梁主缆缆力和吊索索力计算结果非常接近，其中，主缆缆力在加载侧的最大相对误差为0.22%，在非加载侧为0.04%；吊索索力在加载侧与非加载侧的最大相对误差均为2.6%。这说明主缆缆力和吊索索力对等效单梁模型加劲梁刚度影响很小。

3) 解析式(25)的计算结果与空间精细化有限元计算结果相比，加劲梁挠度和扭转角均偏大，两者之间的误差也是由主塔处向跨中逐渐增大。其中，加劲梁挠度相对误差最大为7.1%，相比等效单梁模型有所增大，但扭转角最大相对误差为6.3%，相比等效单梁模型降低了57.1%。产生误差的原因有：实际加劲梁抗弯刚度沿节间长度略有变化，而解析式(25)中的新型板桁加劲梁等效抗弯刚度为定值，相比实际加劲梁刚度偏小，故计算所得挠度偏大；此外，相比于等效单梁模型，解析式(25)中考虑了弦杆纵向约束对加劲梁扭转变形的影响，这在一定程度上提高了扭转角计算精度。对于悬索桥加劲梁刚度初步设计阶段，本文解析式(25)的计算误差总体不超过10%，在可接受范围内。

6 结论

1) 针对无上横联的新型板桁加劲梁，依据剪切刚度等效，构建了闭口薄壁箱形梁连续化等效模型，给出了箱形截面各薄壁等效厚度计算公式。

2) 基于截面刚性周边假定，考虑弦杆纵向约束作用，建立了新型板桁加劲梁连续化等效模型的扭转平衡微分方程，推导得到了扭转角解析公式。采用上述连续化等效方法，依据该解析公式计算所得的新型板桁加劲梁扭转角与由空间精细化有限元模型所得结果较吻合。

3) 弦杆纵向约束作用对新型板桁加劲梁扭转变形的影响不可忽略。算例表明，相比于空间精细化有限元计算结果，考虑弦杆纵向约束时，依据解析式计算所得连续化等效模型扭转角的相对误差最大仅1.2%；不考虑弦杆约束作用时，该相对误差最高达14.9%。

4) 针对新型板桁加劲梁在千米级大跨度悬索桥中的应用，构建了悬索桥连续化等效单梁有限元模型，进一步推导了悬索桥加劲梁扭转角解析式。结果表明，相比于空间精细化有限元模型，连续化等效单梁模型计算所得悬索桥加劲梁挠度和扭转角最大相对误差分别为1.8%和14.7%，依据解析式计算所得相对误差分别为7.1%和6.3%。对于悬索桥加劲梁扭转刚度的设计，上述2种方法的计算误差均在可接受范围内，但计算效率大幅度提高，具有较好的适用性。