正弦脉动激励对气膜冷却特性的影响
2023-09-01王宇楠王春华李录博张靖周
王宇楠,王春华,李录博,张靖周
(南京航空航天大学 能源与动力学院 航空飞行器热管理与能量利用工信部重点实验室,江苏 南京,210016)
随着航空事业的迅猛发展,航空燃气涡轮发动机拥有了更高的性能与效率,但同时涡轮部件的热负荷也不断提升[1]。气膜冷却是一种典型的冷却换热技术[2],冷气通过气膜孔出口流出,一部分与主流发生掺混,其余部分因被主流所压制,贴在壁面处形成一层连续的低温气膜,从而起到保护外部热端部件的作用[3-4]。因此,提升气膜射流冷却能力对于降低涡轮部件热负荷有着重要意义。
然而,传统的气膜冷却展向覆盖率低,并且会在孔出口下游处形成肾形涡对,加剧冷气与主流的掺混,降低冷却效率。一些学者提出,改进冷气孔形状可以作为一种提升气膜冷却效率的手段,比如横槽孔、扇形孔、凹坑孔和收敛缝型孔等[5-7]。近年来,人们把目光集中在了脉动气膜冷却上,即通过对冷气施加一种激励形式,将冷气震荡吹出。它不仅能实现传统气膜冷却的冷却作用,还能将自身的激励特性引入到流场中[8-9]。为了进一步提升冷却效果,脉动气膜冷却已经受到越来越多国内外学者的重视[10]。
学者们对脉动气膜冷却的影响进行了广泛研究[11]。COULTHARD 等[12-13]通过实验阐释了脉动气膜冷却对冷却效果的影响,发现脉冲冷却效果有限,在低吹风比下连续性射流的整体冷却效率更高。JOHARI等[14]对射流的占空比和脉冲频率进行了实验研究,发现在固定的喷射时间内增加占空比可以减少冷气对主流的穿透,主流与次流的掺混率最高增幅可达到50%。在冷却性能方面,BIDAN 等[15]对连续性射流和脉动射流展开研究,发现在相同吹风比和周期相同的情况下,脉动气膜冷却在减少冷气量的同时还具备提高冷却效率的潜力。EKKAD等[16]发现脉动射流可以更好地保护表面。JUNG等[17]在研究中指出脉冲射流相较于传统的气膜冷却可以使冷气更均匀地分布在平板上,并且在流向上获得更高的冷却效率。MULDOON 等[18]采用DNS 方法进行仿真分析,发现脉冲可以增强涡的诱导,且在脉冲启动时,会出现一个起始涡,它可以帮助冷气附着在壁面上。SEO 等[19-20]的实验结果表明,主流脉动可以帮助冷气射流在燃气轮机涡轮表面更均匀地扩散。
大涡模拟(LES)作为一种数值预测湍流运动的工具,不仅能够捕捉到RANS方法非平衡过程中出现的大尺度效应和拟序结构,而且克服了直接数值模拟方法中需要求解所有湍流尺度而带来的巨大计算成本的问题,是目前研究湍流问题中最有效的方法。本研究利用大涡模拟方法,针对正弦脉动气膜冷却射流与平板主流的相互作用展开研究,并结合红外热成像实验测试结果进行验证;重点关注时均吹风比、脉动频率及脉动幅值等参数对涡系结构演化的影响,从时均和瞬态特征两方面针对脉动气膜冷却的流动传热机制进行研究。在关于脉动气膜冷却的研究中,人们大多采用方波激励,但对于不同波形激励展开基础研究也是非常必要的,故本文对冷气侧施加正弦脉动激励,将正弦激励特性引入到流场中,观察脉动频率和幅值在不同吹风比下对气膜冷却流动传热的影响,以期进一步揭示正弦脉动在特定情况下的强化/弱化冷却机制,并为实际情况中根据不同的场景采用不同的脉动频率与幅值提供理论依据。
1 计算方法与模型验证
1.1 物理模型
本文的计算模型如图1所示,包括主流通道、气膜孔和冷气通道3个部分。圆柱孔直径D为5 mm,倾角为35°,高度为3D。主流通道长为30D,宽3D,高6D。冷却通道的长度为15D,宽度为3D,高度为4D。坐标轴的原点位于气膜孔出口中心位置,x、y和z轴分别对应于流向、展向和壁面法线方向。
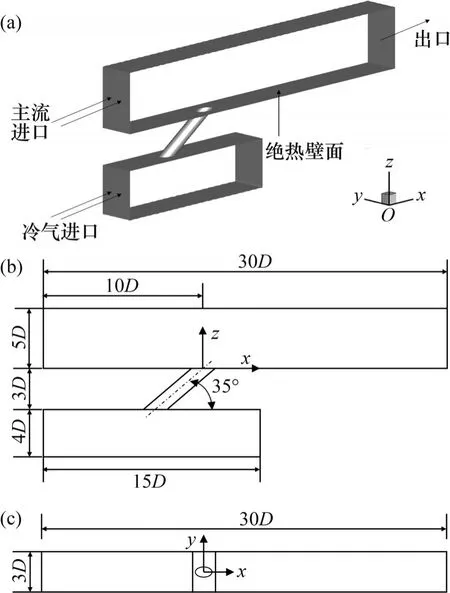
图1 计算模型Fig. 1 Computational model
计算域的边界条件设置如下:主流和冷气入口均设置为速度入口,主流的平均速度为20 m/s,温度为353 K,边界层内速度采用1/7 指数分布规律,主流进口边界层厚度为δ=0.4D,湍流强度为2%。冷气的速度由吹风比决定,其温度为300 K,混合气体出口设置为压力出口,出口静压为一个标准大气压,主流通道和冷气通道两侧壁面均设置为周期性边界条件,并将主流通道的上表面设置为自由流边界,其余面均设为无滑移绝热边界条件。其中,吹风比M是影响气膜冷却性能的关键性热力参数,定义为
气膜冷却效率的计算公式为:
式中:ρ∞和ρc分别为主流和冷气的密度;u∞和uc分别为主流和冷气的平均速度;T∞为主流的来流温度;Taw为绝热壁面温度;Δy为展向距离;η(x,y)为某一位置的绝热气膜冷却效率;Tc为冷气的来流温度;ηloc为局部绝热气膜冷却效率;ηlat为流向平均绝热气膜冷却效率。
1.2 计算方法
本文基于涡黏性的假设[21]来建立应力模型,该模型采用各向同性滤波,假设过滤的小尺度涡为局部平衡状态;涡黏性假设认为非各向同性部分与亚格子黏性系数和大尺度变形张量的乘积成正比。
式中:τij为湍流应力张量;τkk为亚网格各向同性应力;µt为亚网格湍流黏性力;δij为边界层厚度;为应变变化率,
式中:ui和uj分别为滤波后气体速度;xi和xj分别为流动位置;亚格子焓通量qh,j及μt均由Smagorinsky模型定义如下:
本文通过改变冷气进口条件,对比0.5 和1.5这2种吹风比,并计算了5种不同幅值和频率的脉动工况,分别用Case1~Case5 来表示,其中Case5是冷气不加任何脉动的情况。脉动幅值A和频率f的定义如图2所示。图2中,T为冷气脉动变化的1个完整周期;频率f=1/T,这些参数取值如表1所示。

表1 计算工况的脉动参数Table 1 Pulsation parameters for the computation cases

图2 脉动参数定义Fig. 2 Definition of pulsation parameters
用商业软件ANSYS ICEM CFD 19.2 进行结构网格划分,整体和局部的网格划分如图3所示。在气膜孔和壁面附近进行局部加密,在气膜孔出口壁面法线方向网格最大增长率为1.1,为了满足湍流模型中壁面函数的要求,要保证壁面法向即垂直壁面方向的量纲一长度y+≈1。经过网格独立性验证,最后确定总网格单元数约为750万个。

图3 整体网格划分及局部网格划分Fig. 3 Global meshing and local meshing
采用ANSYS FLUENT 软件进行大涡模拟计算。利用Realizblek-ε模型并结合标准壁面函数进行稳态计算,待计算稳定后将其数值作为LES的初始值。压力离散项采用二阶格式,采用最小二乘法离散梯度项。分别采用二阶迎风格式和有界中心差分方法求解能量方程和动量方程。瞬态项的求解采用二阶隐式格式。压力-速度耦合采用SIMPLE 算法实现。为了确保CFL(Courant-Friedrichs Lewy)数小于1.0,在本文中将时间步长设置为10-5s。
1.3 模型验证
为了保证计算结果的准确性,对湍流模型进行验证,将数值模拟结果(7 个周期的平均值)与BIDAN 等[15]实验结果进行对比。图4 所示为在不同吹风比下大涡模拟结果与实验结果对比。实验选取频率f=10 Hz,占空比为0.5,吹风比分别为0.5 和1.0。根据图4(a)和图4(b)可知,数值模拟方法可以较为准确地预测壁面温度变化趋势和数值。在低吹风比下,中心线壁温与展向平均壁温的平均相对误差分别为7.8%和5.3%;在高吹风比下,中心线壁温与展向平均壁温的平均相对误差分别为9.5%和7.2%,这归因于高动量射流引发的流动分离很难被准确捕捉[22]。总体而言,实验结果和LES的仿真结果基本一致。
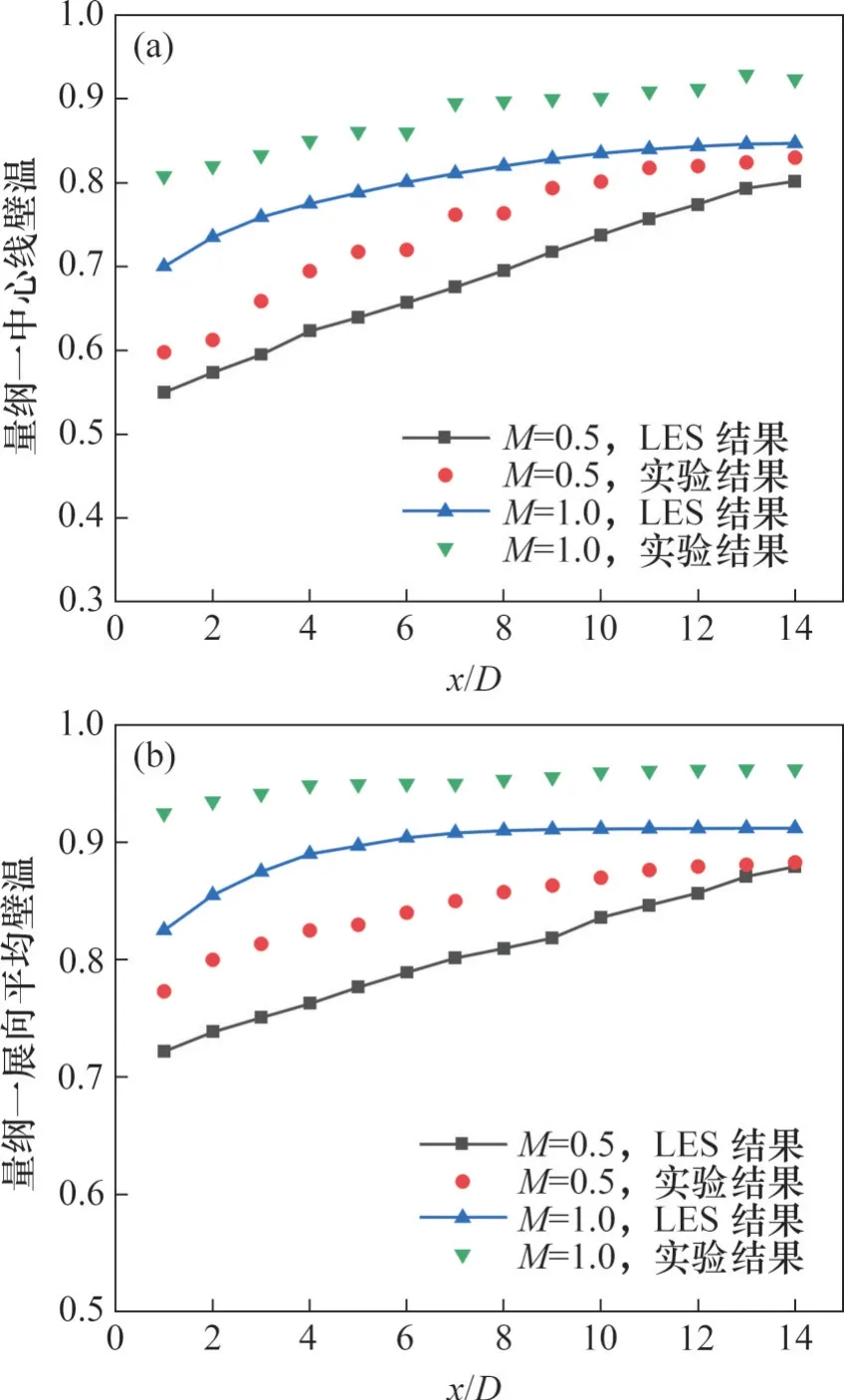
图4 LES结果与实验结果对比Fig. 4 Comparison of LES results and experimental rusults
2 结果分析
2.1 低吹风比(=0.5)
图5所示为绝热壁面沿流向的时均温度分布云图。Θ为量纲一温度,具体公式为Θ=(T∞-T1)/(T∞-Tc),T1为平板上每个点的温度。从图5可知,在低吹风比下,脉动幅值对冷却效率的影响要远大于频率对冷却效率的影响,Case2的平均壁面温度最高,Case5 的平均壁面温度最低,而Case1、Case3、Case4 这3 种情况的平均壁温分布没有出现明显区别。对于Case2,其冷气侧经历周期性脉动激励,其中吹风比最高可达1,最低至0。当吹风比升高时,增强了冷气射流对主流的穿透,此时圆孔下游发生气膜分离,从而降低了冷却效率;而当吹风比过低时,冷气量不足,难以形成良好的气膜保护。随着脉动频率改变,壁面温度并未发生明显变化。Case5的壁面温度最低,说明处于最佳吹风比,冷气紧贴壁面形成了较好的冷气覆盖。
图6 所示为冷却效率沿流向和展向的变化(=0.5)。图6(a)所示为圆孔下游展向平均绝热气膜冷却效率沿流向的变化。在低吹风比下,所有Case 的时均气膜冷却效率沿流向都呈单调递减趋势,其中Case5 冷却效率最高,Case2 冷却效率最低,而Case1、Case3和Case4的冷却效率相差不大且变化规律相同,说明引入脉动冷气的确改变了流动特性,且脉动幅值的影响要大于脉动频率的影响。图6(b)所示为不同流向位置的局部冷却效率沿展向的变化。在流向x/D=4 和x/D=12 两个位置进行对比,发现冷却效率均随着中心线向两侧展向区域逐步递减,且随着流向距离增大,冷却效率也随之降低,但整体规律保持一致。

图6 冷却效率沿流向和展向的变化( =0.5)Fig. 6 Variations of cooling efficiencies with the streamwise and spanwise distances(=0.5)
在气膜孔下游x/D=2截面上的时均流线分布见图7。综合5个Case来看,肾形涡对的尺度最大且占据了主导地位,且在肾形涡对两侧出现了与其旋向方向相反的反肾形涡。肾形涡对将冷气向法向方向上卷吸,从而增强了冷却射流对主流的穿透,同时使得本来附着在壁面的冷气向上抬升,降低了气膜冷却效率。反肾形涡可以抑制冷气的法向抬升,且使得冷气沿展向流动,增强了孔下游展向的冷气覆盖。改变脉动频率对涡对基本没有影响,增大脉动幅值反而会使肾形涡对尺度增大,减弱反肾形涡的强度,降低气膜的贴壁性。

图7 x/D=2.0( =0.5)截面上的流线分布Fig. 7 Streamline distribution on cross-section of x/D=2.0( =0.5)
图8所示为低吹风比下脉动射流(Case2)与连续性射流(Case5)相干结构的比较。其中,t0为起始时刻。从图8(a)可以看到,正弦脉动在T/4 处冷气量达到峰值,此时射流动量增大,加剧了冷气对主流的穿透,降低了冷却效率。由于正弦激励是连续性脉动且具有明显的周期性,所以它产生的气膜也具有明显的周期特征。如文献[12]所述,连续性射流在吹风比为0.5时整体效果最好,射流剪切层涡向下游发展,逐渐演变成一排连续的发夹涡,覆着在墙壁表面。图8(c)所示为两者瞬态拟序结构的局部视图。其中发卡涡头部与射流剪切层涡对应,垂直涡腿与垂直尾迹涡对应,水平涡腿与肾形涡对应[21]。射流剪切层涡加剧了冷气对主流的穿透,肾形涡则将一部分冷气裹挟进主流中,带走了部分冷气,这些都会导致气膜冷却效率下降。对两者进行对比分析,发现脉动射流破碎程度更大,形成了更高强度湍流的脉动特征;而连续性射流的湍流拟序结构形成了平板的边界层特征。
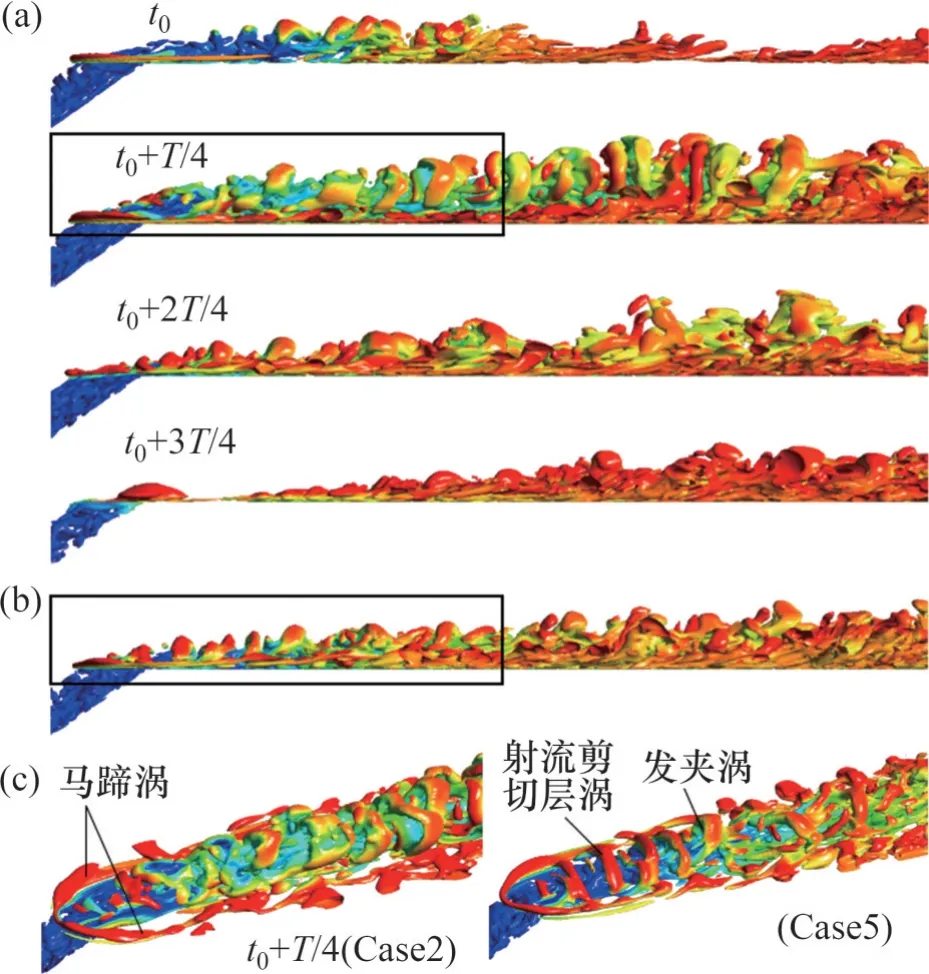
图8 脉动射流和连续性射流相干结构比较( =0.5)Fig. 8 Comparisons of coherent structures in pulsating jet and continuous jet( =0.5)
图9所示为低吹风比下(=0.5)圆孔下游不同截面速度脉动信号的统计学特征。图9(a)所示为湍动能ETKE的分布,其中分别为x、y、z方向的均方根速度。圆孔高湍动能的区域集中在射流出口中心处,射流两侧受马蹄涡的影响,也会出现部分高湍动能区域。与Case5相比,引入脉动射流会明显提升湍动能,当脉动幅值一定时,提高脉动频率后湍动能的增加不太明显,但提高脉动幅值能显著增强湍动能,即冷气与主流的动量交换加强,强化射流与主流之间的相互掺混,导致冷气对壁面的覆盖效果变差。图9(b)所示为中心线上的法向速度均方根分布,可见速度脉动主要集中在边界层内,引入脉动射流会导致增大,且增大脉动幅值会明显提升近壁面x/D=2处的,而且随着流向距离增加,脉动对的影响逐渐减弱。整体而言,脉动频率对圆孔下游湍动能和速度脉动的影响弱于脉动幅值的影响。

图9 速度脉动信号统计( =0.5)Fig. 9 Statistical characteristics of velocity fluctuation(=0.5)
图10 所示为低吹风比(=0.5)下x/D=2.0 处速度波动的功率谱分布,其中探测点处于截面中心正上方垂直高度为0.5D的位置。在频率为1 000~10 000 Hz 的区域内,有一个斜率为-5/3 的线性剖面,这与充分发展的湍流特征一致。
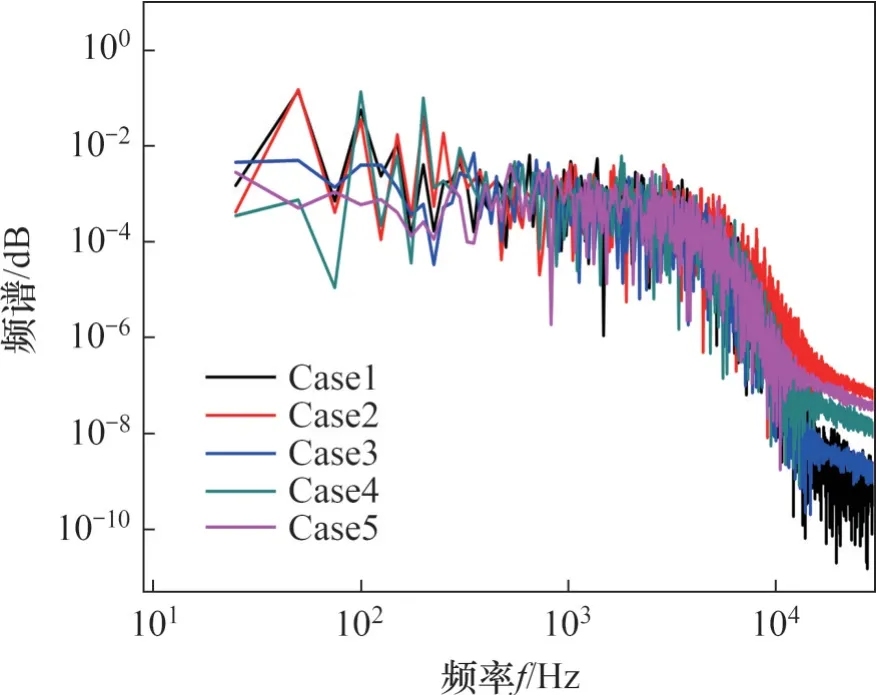
图10 速度脉动的功率谱分析(x/D=2.0)Fig. 10 Power spectrum analysis of velocity fluctuation(x/D=2.0)
2.2 高吹风比( =1.5)
图11 所示为高吹风比(=1.5)下绝热壁面沿流向的时均温度分布。其中,Case5的壁面温度最高,这是因为高动量的射流冲出气膜孔,射流核心位置抬升,没有紧贴壁面形成良好的气膜覆盖。在引入脉动射流后,Case1、Case3和Case4的冷却效果最好,且三者的差异不大,这说明改变脉动频率对冷却效率的影响小。对于Case2而言,它的吹风比最低为0、最高达到3,增大最高吹风比使它的冷却效率下降,壁面温度比Case5的略低但比其余Case 的高,说明在高吹风比下,引入脉动冷气可以提升冷却效率,这与低吹风比时的结论相反。另外,改变脉动幅值对冷却效率的影响较大,这一结论与在低吹风比下的结论一致。率随展向的变化。在展向上仍然是连续性射流的冷却效率最低,在y/D=0.6内的区域冷却效率急剧下降。总体而言,在高吹风比下,引入脉动冷气会提升冷却效率,但是增大脉动幅值后会使提升幅度下降,且改变脉动频率对冷却效率的影响很小。
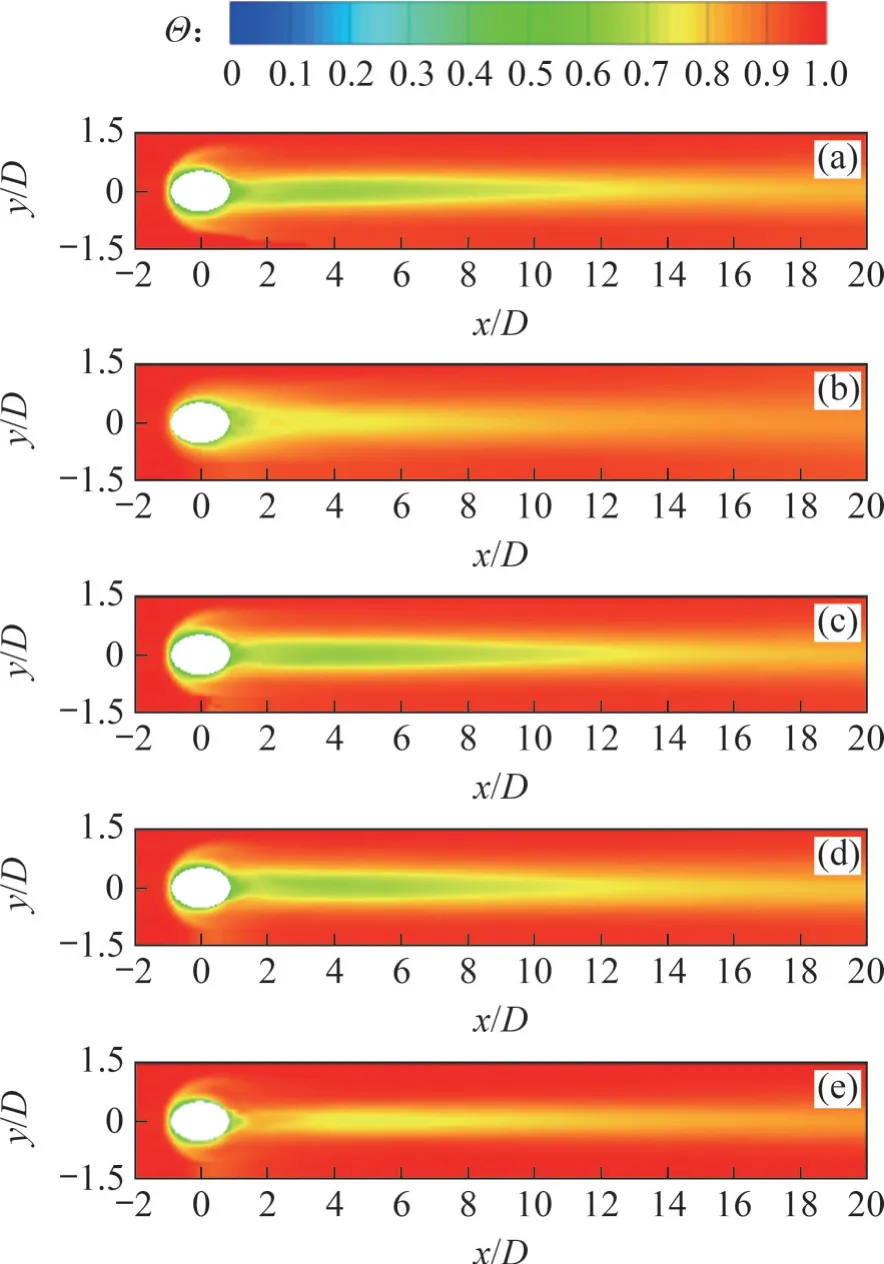
图11 绝热壁面沿流向的时均温度分布( =1.5)Fig. 11 Distributions of streamwise time-averaged temperature on adiabatic wall(=1.5)
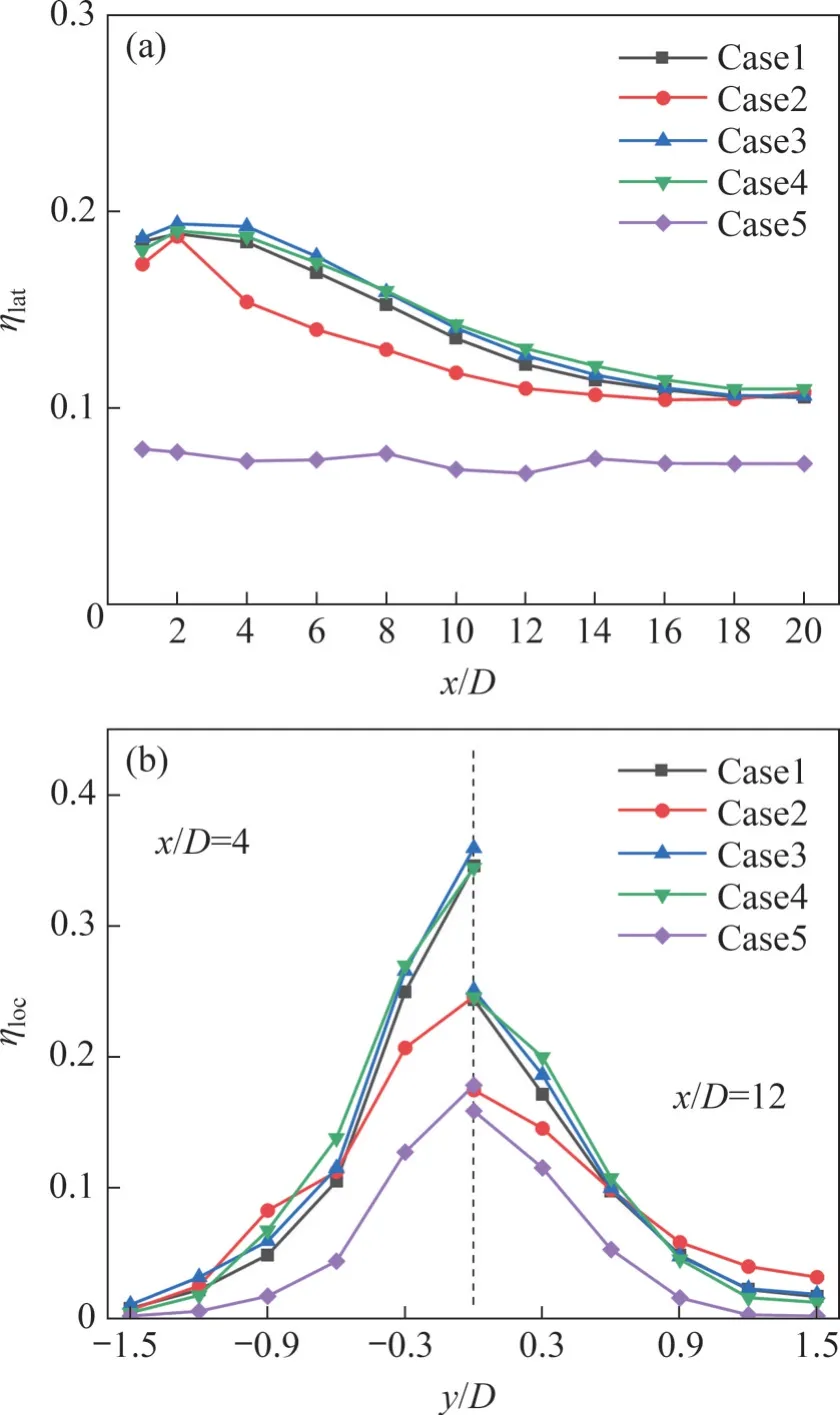
图12 冷却效率沿流向和展向的变化(=1.5)Fig. 12 Variations of cooling efficiencies with the streamwise and spanwise distances( =1.5)
图13所示为高吹风比下x/D=2.0截面上的流线分布。可以明显看到,肾形涡占据了主导地位,并且没有出现反肾形涡。对比其他Case 后发现,引入脉动后肾形涡的尺度明显要大于连续性射流时的涡尺度,随着频率增大,Case1、Case3、Case4的肾形涡对差异并不大,而增大幅值后涡尺度明显增大。
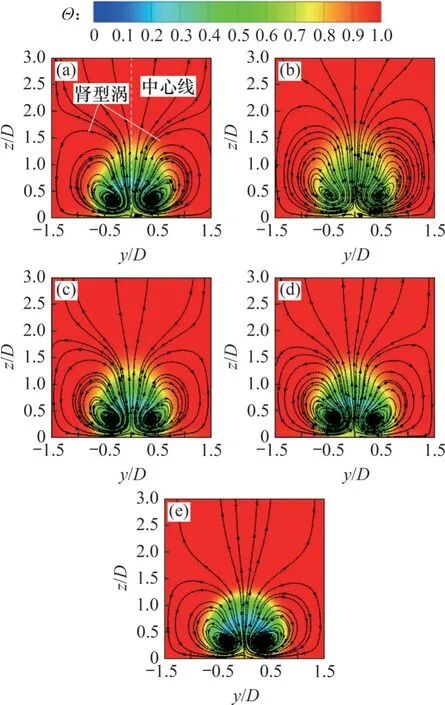
图13 x/D=2.0(=1.5)截面上的流线分布Fig. 13 Streamline distribution on the cross-section of x/D=2.0( =1.5)
图14 所示为高吹风比下脉动射流(Case2)与连续性射流(Case5)相干结构的比较。相较于低吹风比,马蹄涡尺度明显减小。由于冷气动量急剧增大,大量冷气不再附着于壁面,出现流动分离现象,流场中大尺度拟序涡占据了主导地位,冷却效率下降。但和连续性射流相比,由于正弦激励的非连续性射流具有周期性,冷气在部分时刻处于较低水平,可以在一段时间内形成较好的气膜覆盖。因此,在高吹风比下,非连续性射流下的冷却效率比连续性射流下的更高。

图14 脉动射流和连续性射流相干结构比较(=1.5)Fig. 14 Comparisons of coherent structures in pulsating jet and continuous jet( =1.5)
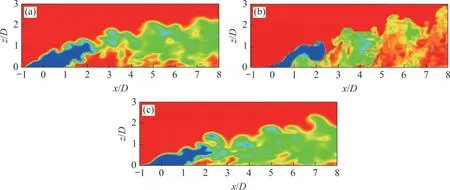
图15 在不同条件下起始涡比较(=1.5)Fig. 15 Starting vortex in different conditions(=1.5)
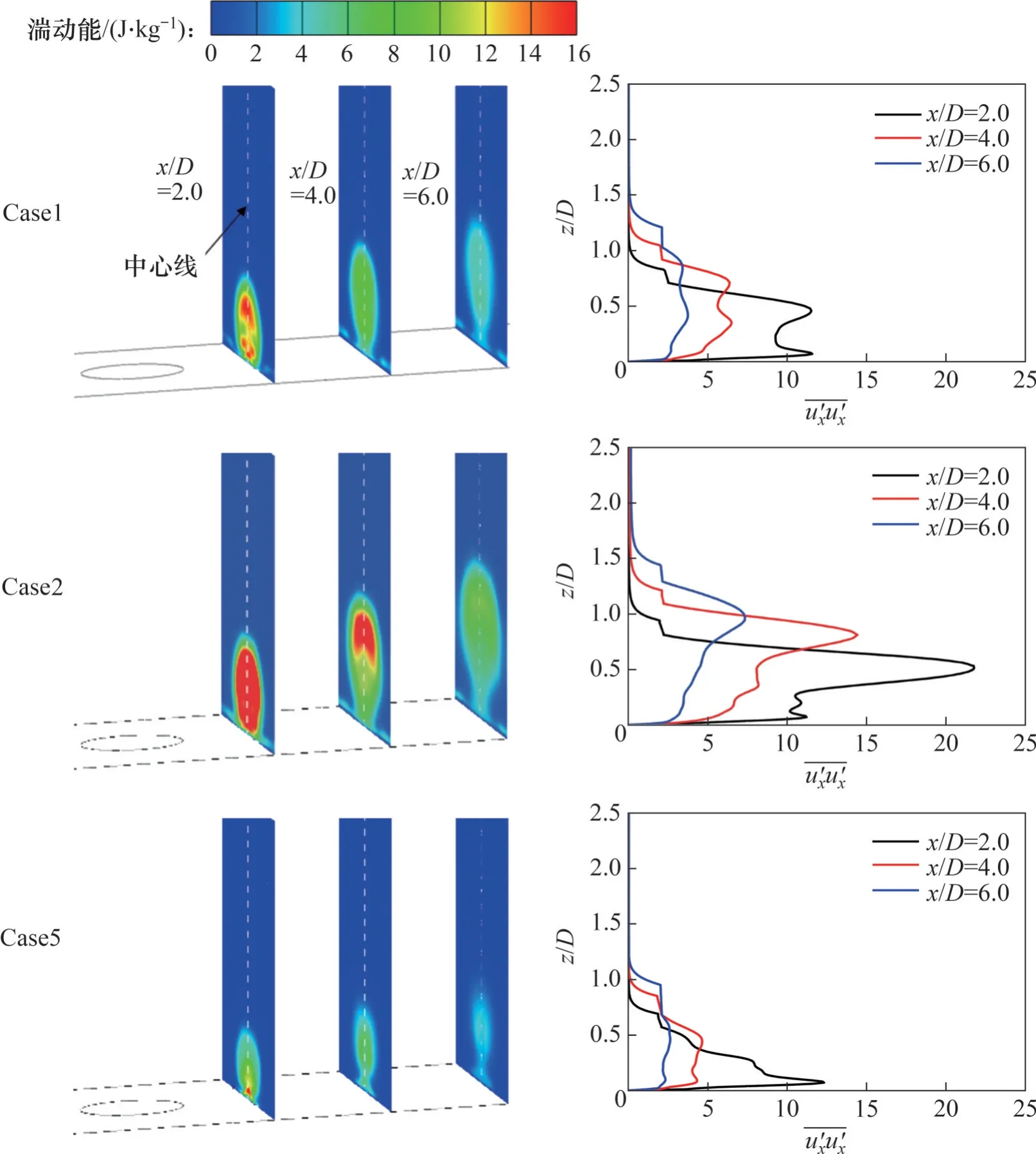
图16 速度脉动信号统计(=1.5)Fig. 16 Statistical characteristics of velocity fluctuation(=1.5)
图17 所示为高吹风比下x/D=2.0 处速度波动的功率谱分布,其中探测点处于截面中心正上方垂直高度为0.5D的位置。在频率为1 000~10 000 Hz 的区域内,也存在一个斜率为-5/3 的线性剖面,说明圆孔出口下游的流动是完全发展的湍流。
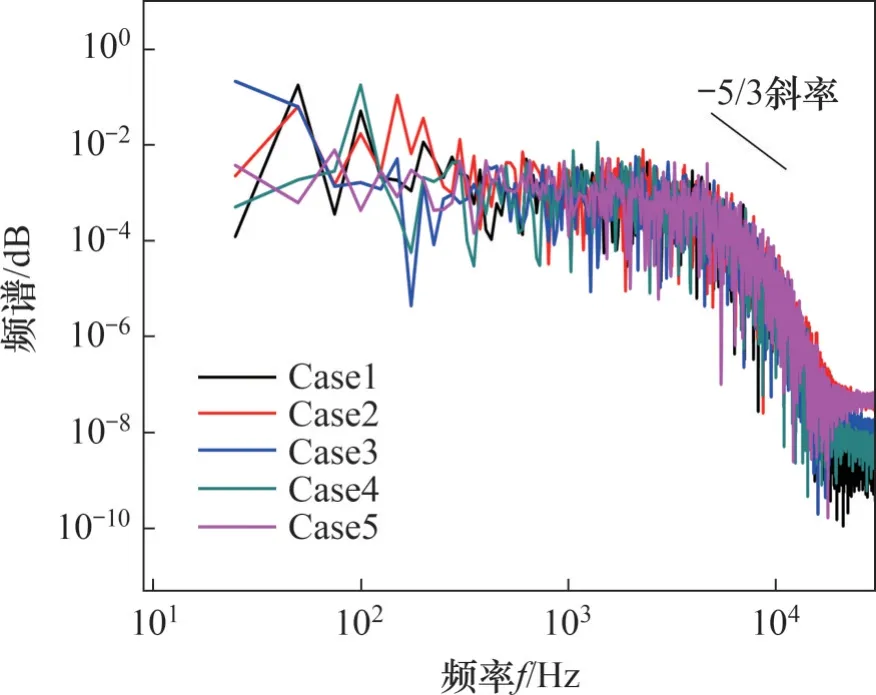
图17 速度脉动的功率谱分析 (x/D=2.0)Fig. 17 Power spectrum analysis of velocity fluctuation(x/D=2.0)
3 结论
2) 在时均流场中,肾形涡对是影响气膜冷却效率的重要结构,高幅值的脉动射流对肾形涡对有促进作用,但改变频率几乎不会影响涡对尺度。
3) 在正弦激励的脉动射流与主流的相干作用下形成了马蹄涡、发夹涡等经典湍流拟序结构。与连续性射流不同的是,脉动射流的涡结构更为无序,形成了更高湍流的脉动特征。由于正弦激励是连续性脉动且具有明显的周期性,没有出现方波脉动那样大尺度起始涡结构,产生的气膜也具有明显的周期特征。
4) 引入脉动冷气可以显著提升湍流动能,且脉动幅值增大会使湍动能急剧增加,但改变频率对湍动能的分布几乎没有影响。由中心线上的法向速度均方根分布可知,引入脉动冷气会导致增大,特别是增大脉动幅值后近孔出流侧这一现象尤为明显,随着流向距离增加,脉动对速度分布的影响也逐渐减弱。
