浅谈三种解析几何中的常考题型

王立奎

(湖北省利川市民族中等职业技术学校,湖北 利川 445400)

高中数学解析几何内容包含各种问题,考查形式灵活多变,掌握更多题型能帮助同学们理解解析几何问题并且高效解答.在众多题型中,与向量结合是最常见的考查形式,除此之外还有和面积、直线相关的常见问题,分析区别并总结这些问题,能提高解题效率和准确度.

1 求向量的倍数λ的取值范围问题

向量和解析几何内容综合在一起考查,一般会把解析几何上的线段看做向量,探讨不同线段之间的等量关系,可总结成一类解析几何中的向量倍数λ大小问题.求解这类问题可以通过构造不等式进行,常用的构造不等式思路包括利用曲线方程中的变量的范围构造、利用判别式构造、利用点与圆锥曲线的位置关系构造等.求解λ的取值范围问题,第一步根据题意确定构造不等式的具体方向;第二步根据图像和相关的圆锥曲线的性质分析题中的几何关系,并列出具体不等式;第三步根据不等式结构特点,结合不同知识点运算得到最终答案[1].

解析根据题意可知,其图像如图1所示:

图1 作y轴垂线

分别作经过曲线C的上顶点A和下顶点B且垂直于y轴的垂线,令这两条垂线与直线l的交点为P、Q,据此进行分析:

①当|DM|>|DN|时:

|DM|≤|DQ|,|DN|≥|DP|,

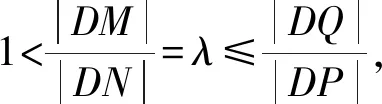
所以1<λ≤3,

②当|DM|<|DN|时,

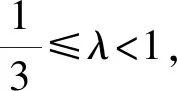
2 求面积最大值问题

解析几何的最大值问题也是常见的一类题型,常以解析几何为载体,对构成的图形面积的最大值考查.求解思路如:利用圆锥曲线的定义、图形对称性和几何性质解题.解答解析几何面积最大值的问题,第一步需要确定题目所求的图形面积的表示公式;第二步根据所求解题目中的已知条件,列出具体解析式;第三步结合相关定义及性质、定理代入具体值计算,进而求得所求最大值即可.

剖析假设圆心O分别到AC、BD弦的距离,再利用圆心到交点的距离OM和四边形的面积公式列出具体式子,运算求解得到所求四边形的面积最大值.

解析根据题目已知条件可知:

假设圆心O到弦AC、BD的距离为d1、d2,

综上所述,四边形ABCD的面积最大值为5.

剖析问题对面积的最大值进行考查,首先确定如何表示四边形面积,结合面积公式对其进行表达,凭借圆的性质对表达式进行简化和替换,进而代入具体值求得最终值[2].

解析如图2所示,作OE⊥AC,OF⊥BD,

图2 向弦作垂线

垂足为E、F,

因为AC⊥BD,

所以四边形OEMF是矩形,

设圆心O分别到弦AC、BD的距离为d1、d2,

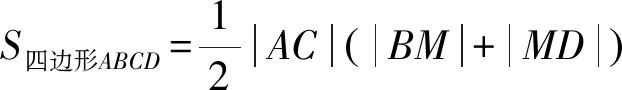
综上所述,四边形ABCD面积最大值是10.

3 求直线斜率k问题

例4已知直线l:y=k(x+2)(k>0)与抛物线C:y2=8x有两个交点A、B,如果抛物线C的焦点为F,且|FA|=2|FB|,则k=____.

剖析首先已知直线解析式不需要对其假设,其次联合抛物线方程式消去变量y得到一元二次方程式,结合已知线段等量关系列式,得到交点坐标之间的关系,并用相关坐标表示斜率,化简即可得知k的具体值.

解析如图3所示,

图3 向准线作垂线

因为抛物线C:y2=8x,

所以焦点F(2,0),准线l:x=-2,

可知直线y=k(x+2)(k>0)经过的定点为P(-2,0),过点A、B作准线l的垂线,垂足为M、N,

即AM⊥l,BN⊥l,

因为|FA|=2|FB|,

故|OB|=|BF|,

因为xB=1,

通过上述三种题型的分析可知,要想正确解答与解析几何相关的问题,不仅需要学生熟练掌握各种圆锥曲线的定义和性质等,还需要学生能够灵活运用所学知识.除此之外,还需要学生具有较强的抽象思维能力和一些相应的解题方法、技巧,才能准确无误地解答这类型题目.希望同学们针对不同类型问题,采取相对应的解题方法进行解答.在解题过程中,加强对问题条件的分析应用,借助已知条件和相关性质去灵活解答,以此提高解题的效率.不同思路对应解题方式各不相同,有助于同学们快速采取正确合理的思路解答这一类问题.