化归思想在高中数学解题中的应用研究

郭琼梅

(泉州第十七中学,福建 泉州 362000)

高中教师应当根据每个学生的不同情况,为学生详细讲解各种数学思想,培养学生举一反三、触类旁通、融会贯通的能力,借助化归思想,学生会养成不断反思、善于总结的学习习惯,且教师也会在该思想的引导下持续关注学生的学习过程,有助于调整教学模式.

1 化归思想的原则

1.1 熟悉化原则

在实际的解题中,运用化归思想,应该是根据以往解题经验为基础,与同种类型的数学题相结合,将其转化成已知量,找到问题的解答思路,教师都应当引导学生通过总结和反思找到应用的优势,并让学生将这些优势内化于心,外化于行.

1.2 简单化原则

在高中数学解题过程中,应用化归思想,其目的是简化数学题目,将数学题目相关的信息进行提炼,实现数学题目的简化,将无价值或者干扰信息剔除,避免解题环节出现错误.

1.3 逆反性原则

化归思想的应用不仅可以单独进行,也可以与其他方法融合使用,如逆向思维,教师让学生根据问题向前推导,总结已知信息之间的关系,也可以达到快速解答问题的目的.

2 化归思想在高中数学解题中的应用措施

2.1 实现动和静之间的转化

化归思想的主要内容就是动和静之间的关系,通常在函数解题中就要借助化归思想,找到各种变量之间的关系,并构建正确的数学模型.在该数学模型中,学生也会对某一数值的运动以及变化规律进行深度探究,再借助相关的函数知识,提炼出各种变量之间的关系,最终把各种静态问题直接转化成动态关系,站在不同的角度,找到函数问题的解答方法[1].

2.2 实现数与形之间的转化

数学知识的学习通常会涉及到数字和图形之间的转化,化归思想中的特别形式也是指代数和图形之间的巧妙转化和结合,这样能够让学生把各种抽象的问题转化为直观形象的问题,便于学生的理解和掌握[2].

分析该题可发现,该题需要求出两个函数在特定区间的交点.教师也会发现,如果只采用传统的教学方式,如利用两个函数相等构建相应的方程、分式和三角函数形式,会加大学生的运算量,甚至还会让部分学生出现难以正确解答的问题.此时,教师可以发挥化归思想的优势,再融合数形结合思想,借助图形分析数量关系,并画出具体的函数图象,如下图1所示.学生通过观察区间[-1,5]上的图象会发现,两个函数图象一共有6个交点,并关于(2,0)成三组对称关系,因此可得出,(2,0)是每组对称点的中点,学生就可轻松求出横坐标.

图1 画图

2.3 实现等价和非等价之间的转化

化归思想中等价转化和非等价转化也属于常见的形式,使用等价转化时,需要对题目中的各种因素进行了解,这样才能够保证转化的正确性.通常情况下,学生在解决翻折、对称的题型时,需要借助曲直转化思想,通过将立体图形转换成平面图形,降低解题难度.

例如,在以下例题中,在直三角柱ABC-A1B1C1中,∠BCA是直角,M是A1B1的中点,N是A1C1的中点,若CC1=CA=BC,求BM和AN所成角的余弦值是____.

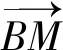
图2 建系

需要注意的是,整个过程中虽然有教师的引领,学生顺利利用化归思想进行等价转化,但教师依旧要向学生强调逻辑准确的重要性,必要的时候结合相关概念,将其转化并顺利求解.

2.4 实现一般和特殊之间的转化

高中数学解题过程中,通常会遇到很多有难度的题,在这样的题目解答中,学生需要使用化归思想,从特殊向一般转化,如特殊值,特殊情况等,再根据题目中的各种已知条件找到特殊值存在的情境[3].

在解答该题目的过程中,学生要仔细分析题目中所包含的已知条件,然后可得出,坐标系所围成的图形面积是确定的,因此该图形的面积和点P位置没有任何关系,这样就可以在解题过程中把P点看做是任意值,然后确定P点的特殊位置,最后根据函数式中a和b的值,求出图形的面积.

2.5 化虚为实,强化学生的化归思想

化归思想的正确运用离不开学生的正确解读,如果学生对化归思想的内涵无法做到深度了解,在具体使用中,也会出现各种问题.为此,课堂上教师就应当为学生多多展示使用化归思想的各种案例,让学生通过不断训练,达到强化理解的目的.

例如,在解答以下例题中

第一题,若关于x的方程9x2+(4+a)3x+4=0,有正解,则实数a的取值范围是____.

第二题,设f(x)是定义在R上的单调增函数,若f(1-ax-x2)≤(2-a),对任意a[-1,1]恒成立,那么x的取值范围为____.

在解答这个题目时,首先,学生会观察到原方程有一定的复杂性,此时可以采用化归思想进行简单处理,设t=3x,则原命题可以等价换成关于t的方程,即

t2=(4+a)t+4=0,

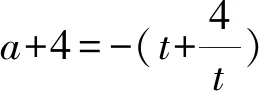
又因为题目中关于x的方程有正解,那么可得出x>0,因此t>0,

所以a+4≤-4,

a≤-8,实数a的取值范围应当在(-∞,-8).

在解答第二题时,也可以由题目得出f(x)在R上是增函数,因此f(1-ax-x2)≤(2-a)

得知1-ax-x2≤2-a,a∈[-1,1]

所以a(x-1)+x2+1≥0,即a∈[-1,1]恒成立.

若g(-1)=x2-x+2≥0,g(1)=x2+1≥0恒成立.

最终得出x≥0或者x≤-1.

2.6 化繁为简,有效借助各种数学定理

在解答立体几何或者不等式以及数列的相关内容题目时,学生都可以使用化归思想.尤其是几何题目,教师应当增强自己对数学教材知识的理解,并学会举一反三,通过对问题进行仔细对比和筛选,逐渐理清解题思路,这样才能够将解题过程不断优化.

例如,在讲解以下例题中,学生就可以借助化归思想进行如下作答.

图3 例题解析

又由点M处于圆C上

得(2x+3-3)2+(-2y+3-3)2=4,即x2+y2=1.

综上所述,在教育改革力度不断加大的当下,培养学生的综合能力已经成为高中数学教学中的基本目标.高中数学教师首先应当意识到课堂上为学生讲授化归思想的重要性,然后要借助各种各样的例题,使学生在不断变化的训练中,强化对化归思想的理解,实现综合能力的发展.