基于分类讨论提高高中生数学解题能力的研究

卢向英

(甘肃省金昌市龙首高级中学,甘肃 金昌 737100)

随着新课改的深入,以数学核心素养的落实来对整个教学的流程及内容进行优化及改进,是促进课程教学深入改革、助力学生综合素质发展的根本要求与必然选择.在数学解题教学中,强化解题思想方法的渗透,帮助学生提高解题能力,已成为当今数学教学的重要任务之一.

1 分类讨论及其在高中生数学解题能力发展中的意义

分类讨论实际上就是由于解题条件存在不确定的情况,为了保证最终问题分析的全面性与准确性,对一切可能存在的解题条件进行分情况讨论,将整个问题相应地划分成若干个小问题来进行分别讨论、分析及求解,最终再将不同分类讨论得到的结果进行汇总.在数学问题解决中,如果可以指导高中生灵活运用分类讨论思想来求解问题,那么可以锻炼学生思维的发散性、严密性与准确性,保证他们在求解问题中可以保持思维的灵动性和能辨性,避免因为思维定势而造成错解问题.特别是数学知识及问题本身的繁杂、抽象等特征非常突出,如果巧用分类讨论思想来分析问题,那么对学生逻辑思维能力和解题能力的发展都有积极的促进作用.当下许多高中生在解题过程中经常出现解题不全面、解题不准确等问题,而造成这些问题出现的原因都是因为自身思维能力和解题能力不足.此时通过有效运用分类讨论思想,对增强学生思维的严谨性,提高数学解题能力等有积极的意义[1].

2 基于分类讨论的高中生数学解题能力提高策略

2.1 运用于求解函数问题

“函数”是高中数学知识体系的重要组成部分,本身涉及到图象、性质、定理等众多方面的知识点,知识的综合性以及相关数学问题本身的繁杂等特性都非常显著.作为高中数学考试的必考知识点,函数部分的数学题型种类繁多,对高中生自身的解题能力要求较高,尤其是容易在该部分数学问题求解中遇到难题,主要表现为答题结果不全面、不完整或者不准确等等[2].比如,许多学生在求解的时候容易忽视函数本身的定义域,以至于因为定义域范围判断不准而影响了最终的解题准确性.而如果可以在指导学生求解函数问题中灵活融合分类讨论思想,那么可以锻炼学生思维的严谨性,让他们可以立足于宏观题干信息与条件视角来对其中的变量、隐含条件或者特殊要求等进行深入把控,并且可以结合实际情况进行分类分析及讨论,确保了整体函数问题求解中学生考虑的全面性,避免因为考虑不周全而直接影响最终的准确解题.

例1已知某一函数f(x)=(m+3)x2m+1+4x-5(x≠0)为一次函数,试求参数m的取值是多少?

分析由于给定的函数f(x)本身已经确定是一次函数,而函数式中相应的包含x的项中的(m+3)x2m+1中的(2m+1)次项或(m+3)系数本身不确定,为了满足实际的求解需求,(2m+1)次项可以为0或1,而(m+3)系数可以为0,这些情况下都能够确保最终所构成的函数为一次函数.在这种分类讨论思路下,学生就可以针对不同分类讨论的情况分别进行列式计算,具体如下:

(2)在2m+1=1,即m=0的时候,相应的函数是f(x)=7x-5,构成了一次函数.

(3)在m+3=0,即m=3的时候,相应的函数是f(x)=4x-5,构成了一次函数.

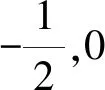
2.2 运用于求解集合问题

集合部分知识是高中数学学习阶段入门的一类基础知识,本身也是高中生最早接触的一类全新的数学内容.虽然这部分知识以及相关类型题本身的求解难度不大,没有涉及到繁琐的计算过程,但是却属于高考数学考试中必考的知识点.通过指导高中生在求解该类数学问题中有效运用分类讨论思想可以有效提高他们解题准确度,增强他们解题的自信心.而分类讨论思想运用主要表现为要指导学生对集合与元素,集合与集合等彼此之间的相应关系开展分类讨论及分析,尤其是针对那些含有参数的集合问题,求解中更是依赖于分类讨论,之后方可借助有效的计算方法来提高整体的问题分析及求解准确性,避免出现重复计算或者遗漏计算等问题[3].

例2已知集合M⊆{1,2,3,4,5},假定a∈M,试求满足(6-1)∈M的非空集合M有多少个?(注:写出相应的集合.)

分析针对本道集合题的求解,如果忽视了分类讨论思想的有效运用,那么会造成解题结果不准确.因为根据题干给出的条件以及待求解的结论,为了保证高中生在解题中做到全面分析,严谨求解,就需要结合集合M当中的实际元素个数开展分类讨论,以保证最终结果的准确性,具体分类讨论结果如下:

(1)如果集合M当中仅包含1个元素,假定3∈M,那么此时可知6-a=6-3=3∈M,故此时相应的集合M为M={1};

(2)如果集合M当中仅包含2个元素,那么这时候满足有关条件的M数目总计为2,即M={1,5},M={2,4};

(3)如果集合M当中仅包含3个元素,那么这时候满足有关条件的M数目总计为2,即M={1,3,5},M={2,3,4};

(4)如果集合M当中仅包含4个元素,那么这时候满足有关条件的M数目总计为1,即M={1,2,4,5};

(5)如果集合M当中仅包含5个元素,那么这时候满足有关条件的M数目总计为1,即M={1,2,3,4,5};

综上所述,满足题干条件的集合M的相应数量总计是7,且分别为{1}、{1,5}、{2,4}、{1,3,5}、{2,3,4}、{1,2,4,5}和{1,2,3,4,5}.

2.3 运用于求解数列问题

数列问题同样是高中数学又一重要问题,主要是等差或等比两种类型的数列.该种类型数学题本身难度不大,但是一般会包含有未知量、变量等,为了可以对相应数列问题进行准确求解,也要注意在求解问题中应用分类讨论思想,更好地帮助高中生对其中包含的数量关系问题或者周期性问题进行求解,降低了相应问题求解的难度[4].因此,在该部分数学题求解教学中,可以选择恰当的一些类型题来帮助学生借助分类讨论的方法来对整个问题求解过程进行简化,保证不断提高他们解题的准确性与效率.

例3 现有一个数列1,2x,3x2,4x3,…,试求其Sn?

分析本道数列问题中没有对数列本身所属的类型进行确定,在实际的求解中许多高中生可能会片面地认为其为等差数列或者等比数列,那么求解问题过程中就容易出现考虑不周的问题.此时如果学生懂得利用分类讨论思想来分析问题,那么可以在分类讨论的过程中快速简化问题求解过程,尤其是注意到对x=0这一特殊情况进行考虑.

假设Sn=1+2x+3x2+4x3+…+nxn-1,之后可以在此基础上进行下述分类讨论:

(1)当x=0时,a1=1,a2=2x=0,a3=3x2=0,…,an=nxn-1=0,这时候化简可以确定Sn=1+2x+3x2+4x3+…+nxn-1=1.

(3)当x≠0且x≠1时,基于Sn=1+2x+3x2+4x3+…+nxn-1①可以相应地得到下式:xSn=x+2x2+3x3+4x4+…+nxn②.

由①-②,得

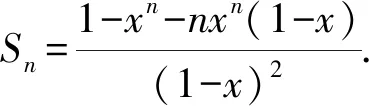
2.4 运用于求解几何问题

几何问题也是高中生觉得难度比较大的一类数学问题,相应的数学知识点在整个数学知识体系中占有较大比重.虽然高中生在经过以前的数学学科知识学习之后对平面几何知识形成了深刻认知,但是在进入高中后碰到立体几何方面知识及问题,却容易因为这些知识或问题的繁杂性特征比较突出而影响了他们学习的效果.在指导高中生求解立体几何问题过程中,为了可以巩固他们课堂所学部分的数学知识,以及提高他们求解几何问题的能力,要注意结合题干信息应用分类讨论思想,对数学问题题干信息进行剖析来确定问题的关键类型,之后结合关键信息来进行认真分析,明确其中可能存在的各种可能情况,并且要逐一列出来,避免因为遗漏而造成解题不准确.

总之,分类讨论是提高高中生数学解题能力和思维能力,助力他们数学综合素质全面发展中非常关键的一种数学思想.在实际的数学问题求解教学中,可以结合集合问题、函数问题、数列问题和几何问题等常见问题,指导学生运用分类讨论去对问题进行分类讨论及求解,保证不断提高他们基于分类讨论思想解题的能力.