基于激电法评价含水合物沉积物渗透率数值模拟研究*

邢兰昌，王 硕，张欢欢，魏 伟，韩维峰，杨金秀，葛新民

基于激电法评价含水合物沉积物渗透率数值模拟研究*

邢兰昌1,†，王 硕1，张欢欢1，魏 伟2，韩维峰2，杨金秀3，葛新民3

（1. 中国石油大学（华东） 控制科学与工程学院，山东 青岛 266580；2. 中国石油勘探开发研究院 新能源研究所，河北 廊坊 065007；3. 中国石油大学（华东） 地球科学与技术学院，山东 青岛 266580）

含水合物沉积物样品渗透率的实验测量过程中存在成本高、周期长、水合物相态变化等问题，水合物开采过程中缺乏可对储层渗透率动态变化进行实时监测的技术。提出基于激电响应评价含水合物沉积物渗透率的新方法，构建含水合物多孔介质的流场与电场有限元数值模型，探讨水合物饱和度、骨架颗粒尺寸等因素对复电导率和渗透率的影响规律及机理，建立基于复电导率参数的含水合物多孔介质渗透率评价模型。研究结果表明：（1）随着多孔介质骨架颗粒粒径及等效孔径的增大，复电导率谱的弛豫时间增大，复电导率虚部极大值所对应频率降低，双电层极化主导频率范围内的复电导率虚部增大，多孔介质有效渗透率增大；（2）随着孔隙填充型水合物的饱和度增加，双电层极化主导的频率范围内复电导率虚部减小，界面极化主导的频率范围内复电导率虚部增大，含水合物多孔介质有效渗透率及其变化率持续减小；（3）双电层极化主导的频率范围内复电导率虚部与渗透率之间存在确定性关系，在饱和水条件下选取的固定频率处复电导率虚部与渗透率呈幂函数关系，结合饱和与非饱和条件下复电导率之间的关系以及归一化渗透率与饱和度之间的关系可建立基于复电导率虚部的含水合物多孔介质有效渗透率评价模型。研究结果可为开发基于激电法的含水合物沉积物样品渗透率实验测量技术以及天然气水合物储层渗透率动态监测技术提供理论与模型基础。

天然气水合物；渗透率；激发极化；复电导率；水合物饱和度；数值模拟

0 引 言

天然气水合物储量巨大，具有能量密度高、清洁无污染等优点，被认为是继页岩气、煤层气、致密气之后最具开采潜力的战略性接续能源[1-2]。我国已完成多次海域天然气水合物试采，为将来实施“生产性试采”奠定了坚实的基础。为了最终实现海域天然气水合物的商业化开发，仍需解决一系列的难题，如具有开采潜力水合物资源的评估、水合物甜点的精准探测、水合物经济高效开采等[3]。我国南海天然气水合物大多赋存于未固结成岩的粉砂、黏土质粉砂、粉砂质黏土等沉积物中，水合物储层呈现高泥质含量、低渗透性和高非均质性等特点[4]。降压试采结果表明，水合物储层渗流能力差、天然气产量低、储层改造困难，尚未达到商业化开采要求。天然气水合物降压开采涉及热量传递、水合物相变分解、气−水两相渗流、储层变形等多个相互耦合的物理/化学过程，储层的温度、孔隙压力、水合物/水/天然气含量等持续发生变化。水合物分解吸热和气流焦耳−汤姆逊效应等综合作用会引起储层局部温度降低，可能导致地层水结冰以及水合物二次生成，此外水合物分解产出的水促使黏土发生体积膨胀，继而堵塞流体流动通道，最终导致地层渗透率显著降低。可见地层中水合物分解所引起的上述系列变化严重制约了天然气产出效率的提升[5-7]。掌握天然气水合物开采过程中储层渗透率的实时变化规律对制定科学、高效的水合物开发方案，评价储层改造效果，以及现场实时调整和动态优化开发策略具有重要的意义。

针对天然气水合物储层的渗透性评价问题，研究人员已经开展了理论分析、数值模拟、实验室测试以及现场原位测试等工作[5-14]。测试含水合物沉积物渗透率的方法可分为流动测试法、非流动测试法以及两者相结合的方法。流动测试法又可分为稳态法和非稳态法，其特点在于测试过程涉及单相或多相流体的渗流过程，属于侵入式、直接式测量方式。典型的非流动测试法包括声波法、电阻率法、基于X射线计算机断层成像（X-ray computed tomography,X-CT）技术以及基于核磁共振（nuclear magnetic resonance, NMR）技术的测试法，其特点在于测试过程中不涉及流体渗流过程，属于非侵入式、间接式测量方式。非流动测试法对渗透率模型的可靠性要求较高。由于水合物对环境条件非常敏感，采用侵入式测量方式的流动测试法在实施过程中容易受到水合物分解、二次形成的影响，从而引入不可预测性测量误差；而采用非流动测试法可以有效地降低上述影响，其中部分方法（如NMR测井法）在储层原位渗透率评价方面更具优势。但是，由于NMR测井存在作业成本高、探测深度较浅等问题，在天然气水合物开采过程中难以对储层渗透率进行实时、长期的远探测。

本文提出基于激电法定量评价天然气水合物储层渗透率的新思路。激电法，又称为激发极化（induced polarization, IP）法，是一种以岩矿石的激电效应、激电特性差异为物理基础的电性勘探方法[15]。激电法可分为时间域激电法和频率域激电法，前者在断电后测量瞬态响应随时间的衰减特性，后者在供电期间记录稳态响应随频率的变化特性。在一定频率范围（如1 mHz ～ 100 Hz）内开展扫频测量可以得到复电导率谱，通过分析复电导率谱来研究地层的激电特性，称为谱激电法（spectral induced polarization, SIP）或复电导率（complex conductivity, CC）法。SIP或CC法是一类低频地电方法，通过将SIP响应参数与多孔介质的结构特征参数相关联，可实现对多孔介质渗透率的定量评价，其基本假设为激电效应主导的电极化（如低频电化学极化）过程的长度尺度与控制渗透率的几何长度尺度密切相关[16-18]。目前，低频段电学阻抗谱方法在天然气水合物相关实验研究中得到了初步应用。TZIRITA等[19]测试了四氢呋喃水合物及其与砂和高岭石混合物的阻抗（50 ～ 1 000 Hz），实验数据展示了水合物体系电学参数的频率依赖特性。DU FRANE等[20]测试了甲烷水合物的阻抗谱（20 Hz ～ 2 MHz）并确定了水合物的电导率，随后对水合物与石英砂和玻璃珠混合物（不含孔隙水）进行了测试[21]，但是在数据分析时把低频（如低于100 kHz）部分作为噪声过大的无效数据进行了舍弃。邢兰昌等[22]测试了四氢呋喃水合物生成和分解过程中的阻抗谱（10 mHz ～ 8 MHz），通过分析等效电路元件参数的变化规律探讨了水合物生成和分解过程的阻抗谱参数特征。李栋梁等[23]利用以甲烷为主的混合气为模拟气在砂岩样品中合成了水合物并测试了其电阻抗（0.05 kHz ～ 200 kHz），结果显示含水合物岩石的介电常数在1 kHz ～ 100 kHz频段呈现频散特性。为了实现基于低频（SIP频率范围）电阻抗谱对松散沉积物中水合物饱和度进行定量评价的目标，邢兰昌等[24-29]开展了系列研究工作，设计了复电阻率/复电导率与声学参数的联合探测（ultrasound combined with electrical impedance, UCEI）系统，在开展水合物模拟实验测试的基础上提取了用于构建电声联合岩石物理模型的有效特征参数，以宽频复电导率谱及其导出参数为基础，结合泥质修正阿尔奇公式、Simandoux公式、Cole-Cole模型、频散度模型等建立了一系列水合物饱和度计算模型，形成了基于SIP的多孔介质中水合物饱和度评价方法。

在提出利用激电法定量评价含水合物沉积物渗透率新思路的基础上，讨论激电效应参数与渗透率的关系模型，建立含水合物多孔介质的流场与电场有限元数值模型，研究水合物饱和度、骨架颗粒尺寸等因素对复电导率和渗透率的影响规律及机理，基于此建立基于复电导率参数的含水合物多孔介质渗透率评价模型，提出有待进一步解决的问题。本研究可为将来开发基于激电法的含水合物沉积物样品渗透率实验测量新技术以及水合物储层渗透率动态监测技术提供理论与模型基础。

1 基于激电法评价渗透率基本原理

1.1 多孔介质复电导率与渗透率

激电响应主要受到岩石的岩性所控制，直接感知矿物与流体之间界面的极化效应[30]。通过对多孔介质进行SIP测量可以获得多孔介质的复电导率，复电导率综合了孔隙水导电、矿物颗粒表面导电、矿物颗粒−流体界面处电化学极化的贡献。颗粒表面电导率可表示为一个复数，其实部描述了电荷沿着颗粒−流体界面的电迁移现象，虚部刻画了电荷在颗粒−流体界面处的极化过程。多孔介质骨架颗粒表面电导率、内比表面积等参数与孔隙尺寸密切相关，而孔隙尺寸是用于预测渗透率的关键参数[31]。

如式（1）所示，多孔介质复电导率可以采用模值与相位角或者实部与虚部的形式来表示。

式中：*为复电导率，S/m；||为复电导率模值，S/m；为相角，rad；′为复电导率实部，S/m；″为复电导率虚部，S/m。

对于饱和水溶液的多孔介质，其复电导率实部可表示为

式中：w为孔隙水的电导率，S/m；为地层因子，结合阿尔奇公式可将表示为

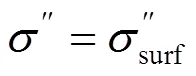
在多孔介质材料中，流体在压力差的作用下发生运移，通常可采用渗透率来定量表示流体流动的难易程度。以达西定律为基础可将多孔介质中流体流动的量表示为

当多孔介质的孔隙被单相流体所饱和时（如上述饱和水溶液的多孔介质），式（6）所定义的渗透率为多孔介质的绝对渗透率；当多孔介质孔隙中含有多相流体时，每相流体的渗透率称为该相流体的有效（绝对）渗透率；有效渗透率与绝对渗透率的比值称为相对渗透率或归一化渗透率[33]。

1.2 多孔介质渗透率计算模型

1.2.1 采用几何尺度参数的模型

将多孔介质的不规则孔隙空间简化为等径平行毛细管束，则对于半径为、长度为的根毛细管束，利用Hagen-Poiseuille方程可以得到总流量为

对比式（6）和式（7）可得渗透率的计算式

实际岩石多孔介质的孔隙空间具有不规则性，流体实际流动路径a比定义压力梯度的直线距离更长。于是可引入迂曲度参数a= (a/)2，用实际路径a替代式（7）中的直线距离可得

(10)

上述推导过程均立足于毛细管截面为圆形的假设，对于非圆形截面的情况，将式（11）拓展为[34-37]

式中：eff为等效水力半径；s为形状因子。

对于具有单一粒径尺寸的球形颗粒多孔介质材料，其渗透率计算式可表示为

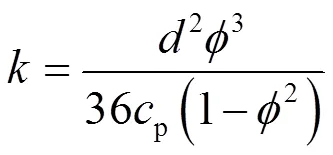
式中：为颗粒直径，m。CARMAN[38]指出对于均匀球形颗粒常数p= 4.8 ± 0.3，通常近似为5。

式中：por为内比表面积。考虑到岩石内比表面积的分形特征，PAPE等[40]提出如下渗透率计算模型：

上述渗透率模型中仅考虑代表几何长度尺度的参数（包含电/水力迂曲度相等的情况），为了实现利用激电参数评价渗透率的目的，需要采用等效的地球物理长度尺度参数[44]。以下将基于SIP参数的渗透率评价模型分为两类，第一类模型采用激电效应的作用强度（以复电导率虚部或极化率来表示）参数来评价渗透率，第二类模型采用激电效应的演化速度（以复电导率谱弛豫时间表示）参数来评价渗透率。

1.2.2 采用激电效应强度参数的模型

基于对激电效应强度与比表面积存在关联的认识，BÖRNER等[30]对泥质砂、粉砂和黏土进行了复电导率测量，证明了复电导率虚部与比表面积存在线性相关性，进而得到以下渗透系数（）计算模型：

式中：为拟合常数（下文相同）；′′(0)为角频率为0时复电导率的虚部，S/m；为渗透系数，m/s。渗透系数与渗透率的关系为=/，其中：为流体的密度，kg/m3；为重力加速度，m/s2。

SLATER等[45]研究了渗透系数模型对松散多孔介质材料的适用性，结果表明地层因子变化范围较小，因此将其忽略，仅利用复电导率虚部对渗透系数进行计算。

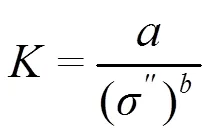
针对Börner模型适用岩性条件范围较窄的问题，SLATER等[46]提出了如下渗透系数模型：

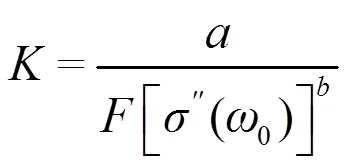
根据水力半径与电荷密度的关系、复电导率虚部与电荷密度的关系以及地层因子与孔隙度的关系，REVIL[47]建立了渗透率、地层因子与复电导率虚部之间的关系模型。

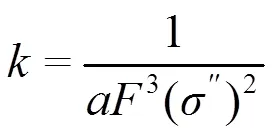
WELLER等[31]测量了从不同地区获取的纯砂岩、泥质砂岩样品的复电导率，利用复电导率虚部和地层因子来计算渗透率。

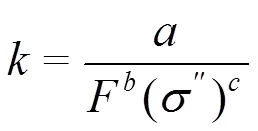
考虑到比表面积、复电导率虚部以及表面电导率等参数之间的比例关系，可将这些参数统一表示为，进而得到以下渗透率计算通式。

1.2.3 采用激电效应速度参数的模型

SCOTT等[48]的研究结果表明，特征孔隙半径与弛豫时间之间存在较强关联。通过对未固结砂进行测试，BINLEY等[49]建立了弛豫时间与渗透系数之间的幂律关系式；此外，KEMNA等[50]的研究结果也表明弛豫时间与渗透率之间存在幂律关系：

ZISSER等[51]建立了弛豫时间、地层因子与渗透率之间的关系模型。

2 含水合物沉积物电场和流场数值模型建立

2.1 数值建模方案

1.2节中所引入的多孔介质渗透率评价模型仅适用于多孔介质被水溶液完全饱和的条件，若要对非饱和条件下多孔介质的有效绝对渗透率进行评价，则需进一步考虑含水饱和度的影响。对于含水合物多孔介质而言，可将其看作孔隙中部分水被水合物所替代的情况，即非饱和条件下的多孔介质包括骨架颗粒、水合物和孔隙水三部分。

基于多物理场耦合计算平台COMSOL Multiphysics建立含水合物沉积物电场和流场的有限元数值模型。首先，建立含水合物多孔介质的几何结构，采用二维几何结构以节省数值计算量，采用圆面代表多孔介质中的骨架颗粒和水合物颗粒；然后，计算并设定含水合物多孔介质中各相的电参数，如带有双电层的骨架颗粒、水合物颗粒、孔隙水；最后，在剖分网格的基础上对电场和流场控制方程进行数值求解，最终计算不同条件下的复电导率和渗透率。

2.2 几何结构与材料参数

图1所示为数值建模中所采用的代表性几何结构，其中水合物以悬浮模式赋存于孔隙空间中。石英砂颗粒直径为48 μm时，多孔介质模型的长度为0.864 mm、宽度为0.432 mm。通过调节水合物颗粒的尺寸以实现对不同水合物饱和度条件的模拟。

图1 二维多孔介质几何结构

为了对流场和电场模型进行求解，需要对材料的特性参数进行设定。孔隙水的密度和黏度分别为1 000 kg/m3和0.001 Pa∙s。采用式（28）对孔隙水的电导率进行计算，孔隙水相对介电常数设定为80。水合物的电导率和相对介电常数分别设定为1 × 10−5S/m和60[20,54-55]。采用文献[27]中的方法对带有双电层的石英砂颗粒的等效电导率和等效介电常数进行计算。

式中：f为孔隙水电导率，S/m；f为孔隙水盐度，mol/L。

2.3 流场/电场控制方程及边界条件

在流场模型中，不可压缩流体的连续性方程为

式中：为速度矢量，m/s。不可压缩流体的动量守恒方程为

式中：为压力，Pa；为单位矩阵；为体积力矢量，N/m3；上标T表示转置运算。通过对以上流动控制方程进行数值求解，可以得到多孔介质出口边界处的质量流量，进而可得到渗流速度。通过联立式（31）和式（32）即可计算得到多孔介质的绝对渗透率。

式中：为渗流速度，m/s；为绝对渗透率，m2；∇为压力梯度，Pa/m；为多孔介质的长度，m。

在电场模型中，交变电场作用下总电流密度为传导电流密度c与位移电流密度d之和。数值模型中求解的电场控制方程如下

式中：为电导率，S/m；为电场强度矢量，V/m；为电位移矢量，C/m2；0为真空中的绝对介电常数，取值为8.854 × 10−12F/m；为相对介电常数。

在流场模型中，将流体入口以及出口均设置为压力边界，入口与出口之间的压差设定为1 000 Pa。在电场模型中，对模型施加交流电场，即在模型左端设置正弦交流电压= sin()，频率范围为1 × 103～ 1 × 106Hz，将模型右端接地。

2.4 网格剖分与数值求解

有限元网格单元的数量直接影响数值计算的稳定性、模型求解所需的时间和算力、模型解的准确度。以下利用模型解的网格依赖性检验来获取合理的有限元网格单元数量。采用自由三角形网格将几何区域离散化。流场求解采用广义最小残差法（generalized minimum residual method, GMRES）；电场计算采用并行稀疏直接法（multi-frontal massivelyparallel sparse direct solver, MUMPS）。以石英砂颗粒直径为48 μm为例，饱和水多孔介质的复电导率虚部和绝对渗透率随网格单元数变化的曲线如图2所示。复电导率虚部和绝对渗透率的数值随着单元数的增加而趋于稳定，当网格数量达到2.41 × 106时，网格单元最大和最小尺寸分别为0.70 μm和8.64 × 10−3μm。

3 含水合物多孔介质渗透率评价模型建立

3.1 石英砂粒径对复电导率/渗透率影响

图3和图4分别展示了水合物饱和度为30%条件下石英砂颗粒粒径不同时多孔介质的复电导率虚部频散曲线和有效绝对渗透率变化曲线。

分析图3可知：①复电导率虚部呈现随频率升高先增大后减小、继而再增大的总体变化趋势，双电层极化和界面极化（Maxwell-Wagner效应）分别在低频段（低于虚部取极大值的频率）和高频段（高于虚部取极小值的频率）占据主导地位，在两者之间的中频段双电层极化强度随着频率升高而减弱、界面极化随着频率升高而增强；②复电导率虚部极大值所对应的频率随着粒径的增大而降低，即弛豫时间随着粒径的增大而增大，已有的理论与实验结果也表明双电层极化弛豫时间与颗粒粒径的平方成正比[56-57]；③在低于虚部极大值所对应频率的频率段范围内（双电层极化主导频率范围），复电导率虚部随着粒径增大而增大，其原因在于弛豫时间增大引起颗粒表面电导率虚部增大，从而使得多孔介质复电导率虚部增大[58]。

图4 有效绝对渗透率随石英砂颗粒粒径的变化趋势

分析图4可知，含水合物多孔介质的有效绝对渗透率随粒径增大而增大，在双对数坐标平面中有效绝对渗透率与石英砂颗粒粒径的平方值呈现近似线性关系（2= 0.996）。当孔隙度保持不变时，颗粒粒径增大的同时颗粒间孔隙尺寸增大，多孔介质样品尺寸不变的条件下则孔隙数量减小。孔隙直径增大引起过流断面面积的增大、孔隙数量减少导致绕流路径缩短，两者均使得渗透率增大[59-62]。

3.2 水合物饱和度对复电导率/渗透率影响

图5和图6分别展示了粒径为48 μm时不同饱和度条件下多孔介质的复电导率虚部频散曲线和有效绝对渗透率变化曲线。

图5 水合物饱和度不同时复电导率虚部的频散曲线

图6 水合物饱和度不同时有效绝对渗透率曲线

分析图5可知，随着测试频率的升高，复电导率虚部随着水合物饱和度的增加呈现先减小后增大的趋势。在双电层极化作用主导的低频范围，颗粒表面电导率虚部随水合物饱和度增加而减小，而颗粒表面电导率近似等于多孔介质复电导率虚部［参见式（5）］；在界面极化作用主导的高频范围，水合物饱和度增加致使界面极化作用增强，导致多孔介质复电导率虚部增大。

分析图6可知，随着水合物饱和度的升高，多孔介质的有效绝对渗透率呈现下降趋势。水合物饱和度的增加使得孔隙空间减小，导致流体可流通孔隙的等效半径减小[63-64]，从而引起渗透率的下降。当水合物饱和度较低时（如图中20%以下），多孔介质有效绝对渗透率下降速率相对较高，这与公开发表的研究结果相一致[65-67]。对于水合物以孔隙填充微观模式赋存于多孔介质中的情况，水合物的形成导致流动通道迂曲度的增加。由于水合物更容易在大孔隙中形成且大孔隙对渗透率的贡献度相对更高，因此在水合物生成初期（水合物饱和度较低时），水合物饱和度的增加所引起的有效绝对渗透率下降速率相对更高。随着水合物饱和度的逐步升高，水合物所占据小孔隙的数量逐渐增多，但是小孔隙对渗透率影响相对较小，因此有效绝对渗透率的下降速率有所降低。

3.3 基于复电导率的渗透率评价模型

以上探讨了水合物饱和度、骨架颗粒粒径对多孔介质复电导率和渗透率的影响规律。在此基础上，首先建立水饱和条件下基于复电导率参数的绝对渗透率评价模型，然后引入水合物饱和度的影响，从而获得含水合物多孔介质的有效绝对渗透率评价模型。

图7展示了水饱和（即无水合物）条件下多孔介质的绝对渗透率与复电导率虚部之间的关系。

图7 多孔介质绝对渗透率与复电导率虚部的关系

分析图7可知，采用幂函数对绝对渗透率与复电导率虚部之间的关系进行拟合可取得良好的效果，拟合模型如式（34）所示（2= 0.993）。

图8 基于复电导率虚部的绝对渗透率模型计算结果

Fig. 8 Calculation results from the absolute permeability model based on the imaginary part of complex conductivity

DAI等[63]提出了以水合物饱和度为变量的归一化渗透率计算模型，如式（35）所示。同时，非水饱和条件下的复电导率虚部可表示为水饱和条件下复电导率虚部和水合物饱和度的函数[27,68]，如式（36）所示。结合式（34）～ 式（36）可得式（37）所示的有效渗透率计算模型。为了提高式（37）中有效渗透率的计算准确度，对常数1进行重新拟合，在式中表示为2。

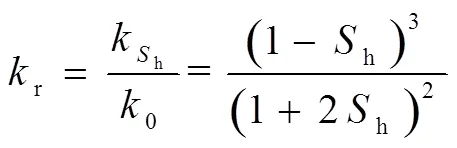
图9所示为多孔介质骨架颗粒粒径为24 μm时，通过式（37）计算得到的有效绝对渗透率与其参考值之间的对比图。其中，常数和2的取值分别为3.0和305。图中可见，在水合物饱和度低于40%范围内，有效绝对渗透率的计算误差均在±15%以内。

图9 基于复电导率虚部的有效绝对渗透率模型计算结果

4 讨 论

4.1 黏土矿物对电场/流场的影响

我国海域天然气水合物主要赋存于未固结成岩的粉砂、黏土质粉砂、粉砂质黏土等沉积物中。其中南海神狐海域水合物储层中多为富含有孔虫等古生物化石的沉积物，沉积物主要成分的粒径低于63 μm[4,14]。黏土具有比表面积大、阳离子交换能力强的特点，从而对复电导率的实部和虚部影响特别显著，同时部分黏土矿物（如蒙脱石）遇水后发生体积膨胀，也会显著降低沉积物的渗透率。

水合物分解产生纯水，从而为黏土矿物的吸水和体积膨胀提供了物质条件，推测可知地层中水合物分解过程中存在因水合物饱和度降低引起的渗透率升高、黏土矿物体积膨胀引起的渗透率降低等相互对立的复杂情况。同时，黏土矿物的类型（如蒙脱石、伊利石、高岭石等）、黏土含量、黏土的微观分布特征（如分散状、层状、包裹状、层状等）均对复电导率的实部和虚部产生显著影响[69-70]。综上所述，黏土矿物对电场和流场参数的影响效应显著、影响规律复杂，需要深入探讨存在黏土矿物条件下的含水合物沉积物的渗透率与复电导率之间的定量关系。

4.2 水合物赋存模式对电场/流场的影响

储层中的天然气水合物以固体相态存在，呈现出多种赋存模式。水合物赋存模式可概括为颗粒排挤型、孔隙浸润型两大类[4]。其中，颗粒排挤型主要包含裂隙填充、脉状、层状等，孔隙浸润型可分为孔隙填充、接触胶结、颗粒包裹、骨架支撑、局部聚集等形式[71]。由于天然气水合物对温度和压力等环境条件非常敏感，水合物分解过程中易出现二次生成的现象，在水合物分解/二次生成等过程中水合物的赋存模式可能发生动态转变。

有研究表明，在水合物饱和度相同的条件下，水合物赋存模式的差异也会导致沉积物的孔隙特征尺寸及其统计分布发生变化，进而引起沉积物复电导率、渗透率的变化。据此可以推测，水合物赋存模式必然影响复电导率与渗透率之间的关系，因此需要深入研究水合物赋存模式对复电导率虚部、渗透率的影响规律与机理。

4.3 渗透率相关激电响应特征参数的提取

多孔介质的孔隙度和孔隙表面积（与孔隙尺寸负相关）是控制多孔介质渗透率的关键参数。有研究人员将直流电导率与多孔介质渗透率相关联[18]。沉积物的直流电导率来源于两类导电机制，即孔隙流体导电、骨架颗粒与流体界面处的双电层导电（即表面电导）。孔隙流体导电机制受到孔隙流体化学性质以及连通孔隙度的影响，而表面电导与沉积物内比表面积有关。对于表面电导足够小并可以忽略的情况（如孔隙水电导率较高），直流电导率与渗透率之间存在正相关关系；然而在表面电导不可忽略的条件下（如较低的孔隙水电导率、含黏土的沉积物等），则表面电导主导多孔介质直流电导率的变化，此时渗透率随着直流电导率的上升而呈现降低的趋势。由以上分析可见，单独利用多孔介质的直流电导率来预测渗透率存在显著的局限性。

从激电效应中可以获得复电导率虚部、弛豫时间等参数，如1.2节中所述，研究人员提出了多个基于激电响应参数的渗透率预测模型，但是这些模型的推广应用遇到困难。在实际应用中，利用激电法测试得到的数据往往受到电磁耦合效应的干扰，如何从激电/电磁耦合响应中分离出真实的激电响应数据是一个具有挑战性的课题。此外，多孔介质的激电响应受到若干物理性、化学性、结构性因素以及测试所采用电场频率的影响，因此激电响应本身具有极高的复杂度。由上可见，即使能够获取真实的激电响应数据，针对含有多种赋存模式水合物的含黏土沉积物，采用何种激电响应参数来建立其与渗透率之间的关系模型以及如何提取出这些参数仍然是值得进一步深入研究的问题。

5 结 论

提出基于激电法定量评价含水合物沉积物渗透率的新思路，构建了含水合物多孔介质的流场与电场有限元数值模型，探讨了水合物饱和度、骨架颗粒尺寸等对复电导率和渗透率的影响规律及机理，建立了基于复电导率参数的含水合物多孔介质渗透率评价模型，提出了值得深入研究的问题。得到以下结论：

（1）建立含水合物沉积物渗透率评价模型的激电响应参数可分为两类，即描述激电效应强度的复电导率虚部或极化率、描述激电效应演化速度的复电导率谱弛豫时间；

（2）多孔介质骨架颗粒粒径增大、等效孔径增大，引起复电导率谱弛豫时间的延长、复电导率虚部极大值所对应频率的降低、双电层极化主导频率范围内复电导率虚部的增大以及多孔介质渗透率的增大；

（3）随着孔隙填充型水合物的饱和度增加，双电层极化主导的频率范围内复电导率虚部减小、界面极化主导的频率范围内复电导率虚部增大，多孔介质渗透率及其变化率持续减小；

（4）双电层极化主导的频率范围内复电导率虚部与渗透率之间存在确定性关系；在饱和水条件下选取的固定频率处的复电导率虚部与渗透率呈幂函数关系，结合饱和与非饱和条件下复电导率之间的关系以及归一化渗透率与饱和度之间的关系可建立基于复电导率虚部的含水合物多孔介质有效渗透率评价模型。

为了开发基于激电法的天然气水合物储层渗透率动态监测新技术，需要深入研究黏土矿物类型及含量、水合物微观赋存模式、骨架颗粒/孔隙尺寸分布、游离气饱和度及微观分布、孔隙水及其与骨架颗粒界面化学性质等因素对沉积物低频交变电场响应和渗流特性的影响规律及机理，设计含水合物沉积物复电导率谱与渗透率联合测试实验装置，在实验的基础上进一步优化激电响应数据处理与特征参数提取方法以及渗透率评价模型。

[1] LI X S, XU C G, ZHANG Y, et al. Investigation into gas production from natural gas hydrate: a review[J]. Applied energy, 2016, 172: 286-322. DOI: 10.1016/j.apenergy. 2016.03.101.

[2] 李清平, 周守为, 赵佳飞, 等. 天然气水合物开采技术研究现状与展望[J]. 中国工程科学, 2022, 24(3): 214-224. DOI: 10.15302/J-SSCAE-2022.03.022.

[3] 孙金声, 程远方, 秦绪文, 等. 南海天然气水合物钻采机理与调控研究进展[J]. 中国科学基金, 2021, 35(6): 940-951. DOI: 10.16262/j.cnki.1000-8217.2021.06.014.

[4] 宁伏龙, 梁金强, 吴能友, 等. 中国天然气水合物赋存特征[J]. 天然气工业, 2020, 40(8): 1-24. DOI: 10.3787/ j.issn.1000-0976.2020.08.001.

[5] REN X W, GUO Z Y, NING F L, et al. Permeability of hydrate-bearing sediments[J]. Earth-science reviews, 2020, 202: 103100. DOI: 10.1016/j.earscirev.2020.103100.

[6] 刘乐乐, 万义钊, 李承峰, 等. 天然气水合物储层有效绝对渗透率现场测试进展[J]. 海洋地质前沿, 2022, 38(11): 40-55. DOI: 10.16028/j.1009-2722.2022.232.

[7] 曾家明, 李栋梁, 梁德青, 等. 天然气水合物储层渗透率研究进展[J]. 新能源进展, 2021, 9(1): 25-34. DOI: 10.3969/j.issn.2095-560X.2021.01.004.

[8] LI G, XU Z L, LI X S, et al. Permeability investigation and hydrate migration of hydrate–bearing silty sands and silt[J]. Journal of natural gas science and engineering, 2021, 89: 103891. DOI: 10.1016/j.jngse.2021.103891.

[9] CHOI J H, MYSHAKIN E M, LEI L, et al. An experimental system and procedure of unsteady-state relative permeability test for gas hydrate-bearing sediments[J]. Journal of natural gas science and engineering, 2020, 83: 103545. DOI: 10.1016/j.jngse.2020.103545.

[10] MAHABADI N, DAI S, SEOL Y, et al. Impact of hydrate saturation on water permeability in hydrate-bearing sediments[J]. Journal of petroleum science and engineering,2019, 174: 696-703. DOI: 10.1016/J.PETROL.2018.11.084.

[11] PAN L L, LEI L, SEOL Y. Pore-scale influence of methane hydrate on permeability of porous media[J]. Journal of natural gas science and engineering, 2021, 87: 103758. DOI: 10.1016/j.jngse.2020.103758.

[12] WU Z R, LIU W G, ZHENG J N, et al. Effect of methane hydrate dissociation and reformation on the permeability of clayey sediments[J]. Applied energy, 2020, 261: 114479. DOI: 10.1016/j.apenergy.2019.114479.

[13] ZHANG Y C, LI C F, MA J S, et al. Investigating the effective permeability evolution as a function of hydrate saturation in the hydrate-bearing sands using a kinetic-theory-based pore network model[J]. Computers and geotechnics, 2022, 150: 104930. DOI: 10.1016/j.compgeo. 2022.104930.

[14] 秦绪文, 陆程, 王平康, 等. 中国南海天然气水合物开采储层水合物相变与渗流机理: 综述与展望[J]. 中国地质, 2022, 49(3): 749-769. DOI: 10.12029/gc20220306.

[15] 何继善. 频率域电法的新进展[J]. 地球物理学进展, 2007, 22(4): 1250-1254. DOI: 10.3969/j.issn.1004-2903. 2007.04.035.

[16] STINGACIU L R, WEIHERMÜLLER L, HABER-POHLMEIER S, et al. Determination of pore size distribution and hydraulic properties using nuclear magnetic resonance relaxometry: a comparative study of laboratory methods[J]. Water resources research, 2010, 46(11): W11510. DOI: 10.1029/2009WR008686.

[17] HUBBARD S S, LINDE N. Hydrogeophysics[EB/OL]. 2011. [2023-03-27]. http://escholarship.org/uc/item/11c8s8d4.

[18] SLATER L. Near surface electrical characterization of hydraulic conductivity: from petrophysical properties to aquifer geometries—a review[J]. Surveys in geophysics, 2007, 28(2/3): 169-197. DOI: 10.1007/s10712-007-9022-y.

[19] TZIRITA A. A study of electrical and thermal properties and their use to detect natural gas hydrates in ocean sediments[D]. College Station: Texas A&M University. 1992.

[20] DU FRANE W L, STERN L A, WEITEMEYER K A, et al.Electrical properties of polycrystalline methane hydrate[J]. Geophysical research letters, 2011, 38(9): L09313. DOI: 10.1029/2011GL047243.

[21] DU FRANE W L, STERN L A, CONSTABLE S, et al. Electrical properties of methane hydrate + sediment mixtures[J]. Journal of geophysical research: solid earth, 2015, 120(7): 4773-4783. DOI: 10.1002/2015jb011940.

[22] 邢兰昌, 陈强, 刘昌岭. 基于电化学阻抗谱测试方法研究四氢呋喃水合物的生成和分解过程[J]. 岩矿测试, 2015, 34(6): 704-711. DOI: 10.15898/j.cnki.11-2131/td. 2015.06.016.

[23] 李栋梁, 卢静生, 梁德青. 祁连山冻土区天然气水合物形成对岩芯电阻率及介电常数的影响[J]. 新能源进展, 2016, 4(3): 179-183. DOI: 10.3969/j.issn.2095-560X. 2016.03.003.

[24] 邢兰昌, 祁雨, 朱泰, 等. 含甲烷水合物沉积物电–声响应特性联合探测: 装置开发与实验研究[J]. 新能源进展, 2018, 6(2): 119-129. DOI: 10.3969/j.issn.2095-560X.2018.02.006.

[25] XING L C, ZHU T, NIU J L, et al. Development and validation of an acoustic-electrical joint testing system for hydrate-bearing porous media[J]. Advances in mechanical engineering, 2020, 12(3): 1-11. DOI: 10.1177/ 1687814020908981.

[26] 邢兰昌, 牛佳乐, 魏伟, 等. 基于宽频复电阻率的含黏土沉积物中水合物饱和度计算方法[J]. 新能源进展, 2020, 8(4): 251-257. DOI: 10.3969/j.issn.2095-560X. 2020.04.001.

[27] XING L C, QI S Y, XU Y, et al. Numerical study on complex conductivity characteristics of hydrate-bearing porous media[J]. Journal of natural gas science and engineering, 2021, 95: 104145. DOI: 10.1016/j.jngse. 2021.104145.

[28] XING L C, NIU J L, ZHANG S L, et al. Experimental study on hydrate saturation evaluation based on complex electrical conductivity of porous media[J]. Journal of petroleum science and engineering, 2022, 208: 109539. DOI: 10.1016/j.petrol.2021.109539.

[29] 徐源, 张欢欢, 邢兰昌, 等. 基于电-力-声多物理场耦合数值模型的含水合物多孔介质声速和衰减特性研究[J].新能源进展, 2022, 10(5): 400-409. DOI: 10.3969/j.issn.2095-560X.2022.05.002.

[30] BÖRNER F D, SCHOPPER J R, WELLER A. Evaluation of transport and storage properties in the soil and groundwater zone from induced polarization measurements[J]. Geophysical prospecting, 1996, 44(4): 583-601. DOI: 10.1111/j.1365-2478.1996.tb00167.x.

[31] WELLER A, SLATER L, BINLEY A, et al. Permeability prediction based on induced polarization: insights from measurements on sandstone and unconsolidated samples spanning a wide permeability range[J]. Geophysics, 2015, 80(2): D161-D173. DOI: 10.1190/geo2014-0368.1

[32] VINEGAR H J, WAXMAN M H. Induced polarization of shaly sands[J]. Geophysics, 1984, 49(8): 1267-1287. DOI: 10.1190/1.1441755.

[33] 蔡建超, 夏宇轩, 徐赛, 等. 含水合物沉积物多相渗流特性研究进展[J]. 力学学报, 2020, 52(1): 208-223. DOI: 10.6052/0459-1879-19-362.

[34] ZHANG Z Y, WELLER A. Fractal dimension of pore-space geometry of an Eocene sandstone formation[J]. Geophysics, 2014, 79(6): D377-D387. DOI: 10.1190/ geo2014-0143.1.

[35] KOSTEK S, SCHWARTZ L M, JOHNSON D L. Fluid permeability in porous media: comparison of electrical estimates with hydrodynamical calculations[J]. Physical review B, 1992, 45(1): 186-195. DOI: 10.1103/ PhysRevB.45.186.

[36] THOMPSON A H, KATZ A J, KROHN C E. The microgeometry and transport properties of sedimentary rock[J]. Advances in physics, 1987, 36(5): 625-694. DOI: 10.1080/00018738700101062.

[37] SCHEIDEGGER A E. The physics of flow through porous media[M]. 3rd ed. Toronto: University of Toronto Press, 1974. DOI: 10.3138/j.ctvfrxmtw.

[38] CARMAN P C. Fluid flow through granular beds[J]. Chemical engineering research and design, 1997, 75(S1): S32-S48. DOI: 10.1016/S0263-8762(97)80003-2.

[39] GUÉGUEN Y, PALCIAUSKAS V. Introduction to the Physics of Rocks[M]. Princeton: Princeton University Press, 1994.

[40] PAPE H, RIEPE L, SCHOPPER J R. A pigeon-hole model for relating permeability to specific surface[J]. The log analyst, 1982, 23(1): 5-13.

[41] JOHNSON D L, KOPLIK J, SCHWARTZ L M. New pore-size parameter characterizing transport in porous media[J]. Physical review letters, 1986, 57(20): 2564-2567. DOI: 10.1103/PhysRevLett.57.2564.

[42] AVELLANEDA M, TORQUATO S. Rigorous link between fluid permeability, electrical conductivity, and relaxation times for transport in porous media[J]. Physics of fluids A: fluid dynamics, 1991, 3(11): 2529-2540. DOI: 10.1063/1.858194.

[43] REVIL A, CATHLES III L M. Permeability of shaly sands[J]. Water resources research, 1999, 35(3): 651-662. DOI: 10.1029/98WR02700.

[44] FIANDACA G, MAURYA P K, BALBARINI N, et al. Permeability estimation directly from logging-while-drilling induced polarization data[J]. Water resources research, 2018, 54(4): 2851-2870. DOI: 10.1002/2017WR022411.

[45] SLATER L, LESMES D P. Electrical-hydraulic relationships observed for unconsolidated sediments[J]. Water resources research, 2002, 38(10): 1213. DOI: 10.1029/2001WR001075.

[46] SLATER L D, GLASER D R. Controls on induced polarization in sandy unconsolidated sediments and application to aquifer characterization[J]. Geophysics, 2003, 68(5): 1547-1558. DOI: 10.1190/1.1620628.

[47] REVIL A. Spectral induced polarization of shaly sands: influence of the electrical double layer[J]. Water resources research, 2012, 48(2): W02517. DOI: 10.1029/ 2011WR011260.

[48] SCOTT J B T, BARKER R D. Determining pore-throat size in Permo-Triassic sandstones from low-frequency electrical spectroscopy[J]. Geophysical research letters, 2003, 30(9): 1450. DOI: 10.1029/2003GL016951.

[49] BINLEY A, SLATER L D, FUKES M, et al. Relationship between spectral induced polarization and hydraulic properties of saturated and unsaturated sandstone[J]. Water resources research, 2005, 41(12): W12417. DOI: 10.1029/2005WR004202.

[50] KEMNA A, MÜNCH H M, TITOV K, et al. Relation of SIP relaxation time of sands to salinity, grain size and hydraulic conductivity[C]//Near Surface 2005-11th European Meeting of Environmental and Engineering Geophysics. Houten: European Association of Geoscientists & Engineers, 2005: cp-13-00047. DOI: 10.3997/2214-4609-pdb.13.P054.

[51] ZISSER N, KEMNA A, NOVER G. Relationship between low-frequency electrical properties and hydraulic permeability of low-permeability sandstones[J]. Geophysics, 2010, 75(3): E131-E141. DOI: 10.1190/1.3413260.

[52] REVIL A, FLORSCH N. Determination of permeability from spectral induced polarization in granular media[J]. Geophysical journal international, 2010, 181(3): 1480-1498. DOI: 10.1111/j.1365-246X.2010.04573.x.

[53] REVIL A, KOCH K, HOLLIGER K. Is it the grain size or the characteristic pore size that controls the induced polarization relaxation time of clean sands and sandstones?[J]. Water resources research, 2012, 48(5): W05602. DOI: 10.1029/2011WR011561.

[54] WAITE W F, SANTAMARINA J C, CORTES D D, et al. Physical properties of hydrate-bearing sediments[J]. Reviews of geophysics, 2009, 47(4): RG4003. DOI: 10.1029/2008RG000279.

[55] HAUKALID K, FOLGERØ K, BARTH T, et al. Hydrate formation in water-in-crude oil emulsions studied by broad-band permittivity measurements[J]. Energy & fuels, 2017, 31(4): 3793-3803. DOI: 10.1021/acs.energyfuels. 6b03416.

[56] TITOV K, KOMAROV V, TARASOV V, et al. Theoretical and experimental study of time domain-induced polarization in water-saturated sands[J]. Journal of applied geophysics, 2002, 50(4): 417-433. DOI: 10.1016/S0926-9851(02)00168-4.

[57] LEROY P, REVIL A, KEMNA A, et al. Complex conductivity of water-saturated packs of glass beads[J]. Journal of colloid and interface science, 2008, 321(1): 103-117. DOI: 10.1016/j.jcis.2007.12.031.

[58] REVIL A. Effective conductivity and permittivity of unsaturated porous materials in the frequency range 1 mHz–1GHz[J]. Water resources research, 2013, 49(1): 306-327. DOI: 10.1029/2012WR012700.

[59] SHEPHERD R G. Correlations of permeability and grain size[J]. Groundwater, 1989, 27(5): 633-638. DOI: 10.1111/j.1745-6584.1989.tb00476.x.

[60] GHASSEMI A, PAK A. Pore scale study of permeability and tortuosity for flow through particulate media using Lattice Boltzmann method[J]. International journal for numerical and analytical methods in geomechanics, 2011, 35(8): 886-901. DOI: 10.1002/nag.932.

[61] 乔太斌, 杨玉双, 李如如, 等. 多孔介质中固体体积分数与颗粒尺度对流体绝对渗透率的影响[J]. 山西大学学报(自然科学版), 2017, 40(1): 92-99. DOI: 10.13451/ j.cnki.shanxi.univ(nat.sci.).2017.01.013.

[62] 杨斌, 徐曾和, 杨天鸿, 等. 高水力梯度条件下颗粒堆积型多孔介质渗流规律试验研究[J]. 岩土力学, 2018, 39(11): 4017-4024. DOI: 10.16285/j.rsm.2017.0643.

[63] DAI S, SEOL Y. Water permeability in hydrate-bearing sediments: a pore-scale study[J]. Geophysical research letters, 2014, 41(12): 4176-4184. DOI: 10.1002/2014GL060535.

[64] 李世龙, 李刚, 魏纳, 等. 含甲烷水合物的石英砂渗透率实验和分形模型对比研究[J]. 新能源进展, 2020, 8(4): 264-271. DOI: 10.3969/j.issn.2095-560X.2020.04.003.

[65] CHEN Y, SUN B J, CHEN L T, et al. Simulation and observation of hydrate phase transition in porous medium via microfluidic application[J]. Industrial & engineering chemistry research, 2019, 58(12): 5071-5079. DOI: 10.1021/acs.iecr.9b00168.

[66] LUO Y, SUN Y, LI L, et al. Image-based pore-network modeling of two-phase flow in hydrate-bearing porous media[J]. Energy, 2022, 252: 124044. DOI: 10.1016/j. energy.2022.124044.

[67] XU J C, BU Z W, LI H Y, et al. Pore-scale flow simulation on the permeability in hydrate-bearing sediments[J]. Fuel, 2022, 312: 122681. DOI: 10.1016/j.fuel.2021.122681.

[68] DENG Y P, SHI X Q, REVIL A, et al. Complex conductivity of oil-contaminated clayey soils[J]. Journal of hydrology, 2018, 561: 930-942. DOI: 10.1016/j. jhydrol.2018.04.055.

[69] XING L C, ZHANG H H, WANG S, et al. Pore-scale modelling on complex-conductivity responses of hydrate-bearing clayey sediments: implications for evaluating hydrate saturation and clay content[J]. Geoenergy science and engineering, 2023, 221: 211356. DOI: 10.1016/j. geoen.2022.211356.

[70] XING L C, ZHANG S L, ZHANG H H, et al. Saturation estimation with complex electrical conductivity for hydrate-bearing clayey sediments: an experimental study[J]. Journal of ocean university of China, 2023. DOI: 10.1007/s11802-023-5492-x.

[71] DAI S, SANTAMARINA J C, WAITE W F, et al. Hydrate morphology: physical properties of sands with patchy hydrate saturation[J]. Journal of geophysical research: solid earth, 2012, 117(B11): B11205. DOI: 10.1029/ 2012jb009667.

Numerical Study on Permeability Evaluation for Hydrate-Bearing Sediments Based on Induced Polarization Principle

XING Lanchang1,†, WANG Shuo1, ZHANG Huanhuan1, WEI Wei2,HAN Weifeng2, YANG Jinxiu3, GE Xinmin3

(1. College of Control Science and Engineering, China University of Petroleum (East China), Qingdao 266580, Shandong, China;2. Department of Alternative Energy, PetroChina Research Institute of Petroleum Exploration & Development, Langfang 065007, Hebei, China; 3. School of Geosciences, China University of Petroleum (East China), Qingdao 266580, Shandong, China)

There are significant problems such as high cost, long period and phase-state change of hydrate in the experimental process for measuring the permeability of hydrate-bearing samples. Moreover, real-time monitoring technologies for the dynamic evolution of reservoir permeability in hydrate exploitation processes are still lacking. A new method for evaluating the permeability of hydrate-bearing sediments based on induced polarization (IP) responses was proposed, and finite-element numerical models of flow field and electrical field for hydrate-bearing porous media were constructed. The effects and corresponding mechanisms of hydrate saturation and skeleton particle size on the complex conductivity and permeability were analyzed. Finally, a permeability evaluation model of hydrate-bearing porous media based on complex conductivity was established. It was demonstrated that: (1) with the increase of the skeleton particle size and the equivalent pore diameter of porous medium, the relaxation time of the complex-conductivity spectrum increases, the frequency corresponding to the maximum imaginary complex conductivity decreases, the imaginary complex conductivity within the frequency range of electrical-double-layer (EDL) polarization increases, and the effective permeability of the porous medium increases; (2) with the increase of the pore-filling-hydrate saturation, the imaginary complex conductivity within the frequency range of EDL polarization decreases, the imaginary complex conductivity within the frequency range of interface polarization increases, and the effective permeability and its changing rate of the hydrate-bearing porous medium decrease continuously; (3) there is a definite relationship between the imaginary complex conductivity and permeability within the frequency range of EDL polarization; the imaginary complex conductivity at a fixed frequency under water-saturated conditions exhibits a power-law relationship with permeability; combining the relationship between the complex conductivity under saturated/unsaturated conditions and that between the normalized permeability and saturation, an evaluation model for the effective permeability of hydrate-bearing porous media can be established based on the imaginary complex conductivity. This study can provide a theoretical and model basis for the development of an experimental measurement technology for the permeability of hydrate-bearing samples based on IP principle and a dynamic monitoring technology for the permeability of natural gas hydrate reservoirs.

natural gas hydrate; permeability; induced polarization; complex conductivity; hydrate saturation; numerical simulation

2095-560X（2023）04-0320-13

TK01；P631

A

10.3969/j.issn.2095-560X.2023.04.004

2022-12-21

2023-03-27

中石油“十四五”前瞻性基础性重大科技项目（2021DJ4901）；国家留学基金项目（202106455003）；中央高校基本科研业务费专项资金项目（20CX05005A）；中国石油科技创新基金项目（2018D-5007-0214）；山东省自然科学基金项目（ZR2019MEE095）

邢兰昌，E-mail：xinglc@upc.edu.cn

邢兰昌, 王硕, 张欢欢, 等. 基于激电法评价含水合物沉积物渗透率数值模拟研究[J]. 新能源进展, 2023, 11(4): 320-332.

： XING Lanchang, WANG Shuo, ZHANG Huanhuan, et al. Numerical study on permeability evaluation for hydrate-bearing sediments based on induced polarization principle[J]. Advances in new and renewable energy, 2023, 11(4): 320-332.

邢兰昌（1983-），男，博士，副教授，硕士生导师，主要从事天然气水合物与多相流相关检测理论与方法、多物理场耦合数值模拟方法、智能感知与检测技术、计算机测控系统研究。

王 硕（1997-），女，硕士研究生，主要从事天然气水合物与多相流相关检测及数值模拟方法的研究。

张欢欢（1997-），女，硕士研究生，主要从事天然气水合物与多相流相关检测及数值模拟方法的研究。