基于HBA-ICEEMDAN和HWPE的行星齿轮箱故障诊断*

2023-08-31陈爱午王红卫

机电工程 2023年8期

陈爱午,王红卫

(1.江苏联合职业技术学院泰兴分院,江苏泰兴 225400;2.东南大学机械工程学院,江苏南京 210096)

0 引言

行星齿轮箱目前被广泛应用于风力发电领域。由于工作环境恶劣,齿轮箱轮齿的关键部位易发生点蚀、断齿等单点故障或复合故障,若故障持续演化将诱发严重的安全事故。因此,准确可靠地检测行星齿轮箱的故障具有重大意义[1,2]。

目前,研究人员一般基于振动信号来对行星齿轮箱进行故障诊断和健康监测[3,4]。李昌林等人[5]提出了集成经验模态分解(ensemble empirical mode decomposition,EEMD),利用EEMD引入白噪声,对振动信号进行分解,以改变信号的极值特征;但EEMD依然存在模态混叠现象。TORRES M E等人[6]提出了自适应噪声完备经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEE-MDAN),在信号分解过程中引入自适应的白噪声使重构信号非常精确;但CEEMDAN分解的分量中依然存在噪声和伪分量。为此,COLOMINAS M A等人[7]对CEEMDAN进行了优化,提出了改进自适应噪声完备经验模态分解(ICEEMDAN),改善了IMF分量的噪声残留问题。顾云青等人[8]将ICEEMDAN与排列熵相结合,用于提取滚动轴承的故障特征,结果证明了ICEEMDAN的优越性;但ICEEMDAN方法的参数均人为设置,盲目设置参数无法发挥算法的最佳性能。为实现EEMD参数的自适应设置目的,CHEN WEI-jia等人[9]利用人工蜂群算法对EEMD的参数进行了优化,实现了噪声幅值系数自适应设置的目的;但其未对总体平均次数进行优化。王海锋等人[10]采用细菌觅食算法对EEMD的噪声幅值系数和总体平均次数进行了协同优化,取得了较好的优化结果;但EEMD的性能不佳。

针对ICEEMDAN的参数优化问题,笔者引入蜜獾算法(HBA)对ICEEMDAN的参数进行优化搜索,以实现参数自适应最优化设置的目的,并利用HBA-ICEEMDAN剔除行星齿轮箱振动信号中的噪声。

完成行星齿轮箱振动信号的降噪重构后,需要进行特征提取。以样本熵和排列熵为代表的特征提取指标目前被广泛用于行星齿轮箱的故障诊断中[11]。但上述指标均只是从单一尺度来表征信号的复杂度,难以全面地描述信号的故障特性。

为此,谢棕等人[12]采用多尺度排列熵(multiscale permutation entropy,MPE)提取齿轮信号的故障特征,取得了较高的识别准确率;但MPE无法提取信号的高频信息。黄海滨[13]基于层次分析和排列熵,提出了层次排列熵(hierarchical permutation entropy,HPE)方法,并用于滚动轴承的故障诊断,结果表明,相较于MPE,HPE对特征提取得更加全面和充分;但HPE忽略了信号的幅值信息,特征存在遗漏。

针对上述问题,笔者提出一种基于HBA-ICEEM-DAN、层次加权排列熵(HWPE)的行星齿轮箱故障特征提取方法。

该方法利用HBA-ICEEMDAN的自适应信号分解优势,结合HWPE的特性(能够准确反映齿轮箱信号动态特性),完成信号的故障特征提取工作;最后,采用支持向量机(经灰狼算法优化的)对行星齿轮箱的故障进行诊断。

为验证行星齿轮箱故障诊断方法的有效性和优越性,笔者设置多组对比实验,进行多个维度的综合分析,包括信号分解算法对比、熵值方法对比和分类器对比实验。

1 算法原理

1.1 蜜獾算法优化的改进自适应噪声完备经验模态分解

1.1.1 改进自适应噪声完备经验模态分解

ICEEMDAN方法中加入的是第h个IMF分量(白高斯噪声经过EMD分解后获得),是一种特殊的噪声Eh[wi]。ICEEMDAN的计算过程如下:

1)向原始信号X中添加白噪声E1[wi]:

X(i)=X+β0·E1[wi]

(1)

式中:wi为被加入的第i个白噪声;

2)利用ICEEMDAN方法对原始信号进行分解,得到第1个IMF分量:

(2)

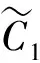
3)求解第2个IMF分量:

(3)

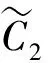
4)以此类推,能够得到第h个IMF分量:

(4)

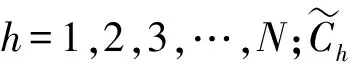
1.1.2 蜜獾算法

通过模拟蜜獾挖掘和觅食蜂蜜的行为,HASHIM F A[14]提出了蜜獾算法,原理如下:

1)种群初始化

随机初始化蜜獾个体的坐标:

xi=lbi+r1·(ubi-lbi)

(5)

式中:xi为第i个蜜獾个体的坐标;ubi,lbi为寻优空间的上边界和下边界;r1为[0,1]内的随机变量;

2)嗅觉系数定义

嗅觉系数Ii与蜜獾和蜂蜜之间的距离di以及蜂蜜的聚集程度S相关,可写为:

(6)

S=(xi-xi+1)2

(7)

di=xprey-xi

(8)

式中:r2为[0,1]内的随机变量;

3)密度因子更新

密度因子a的大小随着迭代次数的增加而不断衰减,以保证从探索到采集的平滑过渡,可写为:

a=C·exp(-t/tmax)

(9)

式中:t为当前迭代次数;tmax为总的迭代次数,C为不小于1的常数(默认为2);

4)个体坐标更新

蜜獾坐标的更新包括挖掘阶段和采蜜阶段。在挖掘部分,蜜獾在蜂巢周围搜寻,其坐标的更新基于嗅觉系数Ii、蜜獾和蜂蜜之间的距离di和密度因子a。挖掘部分的数学形式如下:

xnovel=xprey+F·β·Ii·xprey+F·r3·

a·di·|cos(2π·r4)·[1-cos(2π·r5)]|

(10)

式中:r3,r4,r5为[0,1]内的随机变量;β≥1(默认为6)为蜜獾得到蜂蜜的能力;xprey为蜂蜜的坐标,也即最佳个体的坐标;F为方向控制系数,能够增强蜜獾探索的全局性能。

F的算式如下:

(11)

式中:r6为[0,1]内的随机变量。

在采蜜部分,蜜獾追寻向导鸟直接往蜂巢移动,蜜獾根据距离信息di在xprey周围进行探索。在该部分,探索受密度因子a的影响,探索的数学形式为:

xnovel=xprey+F·r7·a·di

(12)

式中:r7为[0,1]内的随机变量。

1.1.3 参数优化流程

由于ICEEMDAN方法的分解效果取决于白噪声幅值权重(Nstd)和噪声添加次数(NE),因此,笔者采用HBA对ICEEMDAN的2个参数进行优化,适应度函数采用包络熵,当适应度值越小,则代表分解的效果越好;通过优化和更新,来确定最终的最佳参数组合(Nstd,NE)。

优化的步骤如下:

1)HBA算法的种群初始化,设置HBA的迭代次数和种群规模,并设置ICEEMDAN算法的参数优化范围;

2)利用ICEEMDAN分解齿轮箱振动信号,并计算各个IMF分量的包络熵,以包络熵的最小值为适应度函数;

3)判断优化是否达到算法的终止条件,若是,则继续下一步;若否,则更新种群位置,并返回第2)步;

4)保存最优的ICEEMDAN参数组合,并将其代入至ICEEMDAN中,为ICEEMDAN构建HBA算法;

5)利用HBA-ICEEMDAN方法分解齿轮箱振动信号,得到最佳的IMF分量。

1.2 层次加权排列熵

加权排列熵仅从单一尺度来描述信号的动态特性,描述得不够全面,为此,陈柯宇等人[15]提出了多尺度加权排列熵(multi为scale weighted permutation entropy,MWPE),实现了信号多尺度计算的目的。但粗粒化处理本质上是一个低通滤波器,其过滤了信号的高频特征信息,因此,笔者采用层次处理方式对时间序列进行分割,结合加权排列熵,提出了层次加权排列熵[16]。

HWPE能够同时提取信号的低频和高频节点信息,对信号进行全面分析,计算流程如下:

1)对于信号{u(i),i=1,…,N},定义平均算子Q0和差分算子Q1,公式如下:

(13)

(14)

其中,N=2n,n是正整数。算子Q0和Q1的长度为2n-1。

利用算子Q0和Q1,则原始信号可以重构为:

u={Q0(u)j+Q1(u)j,Q0(u)j-

Q1(u)j}j=0,1,2,…,2n-1

(15)

当j=0或j=1,定义矩阵Qj算子如下所示:

Qj(u)=

(16)

2)生成一个n维向量[δ1,δ2,…,δn]∈{0,1},则定义整数γ为:

(17)

其中,正整数γ对应于向量[δ1,δ2,…,δn];

3)在向量[δ1,δ2,…,δn]∈{0,1}的基础上,定义信号u(i)的每一层分解的节点序列如下:

uk,e=Qδn·Qδn-1·…·Qδ1(u)

(18)

式中:k为层次分解中的第k层。

当k=2时,原始信号的两层层次分解的示意图如图1所示。

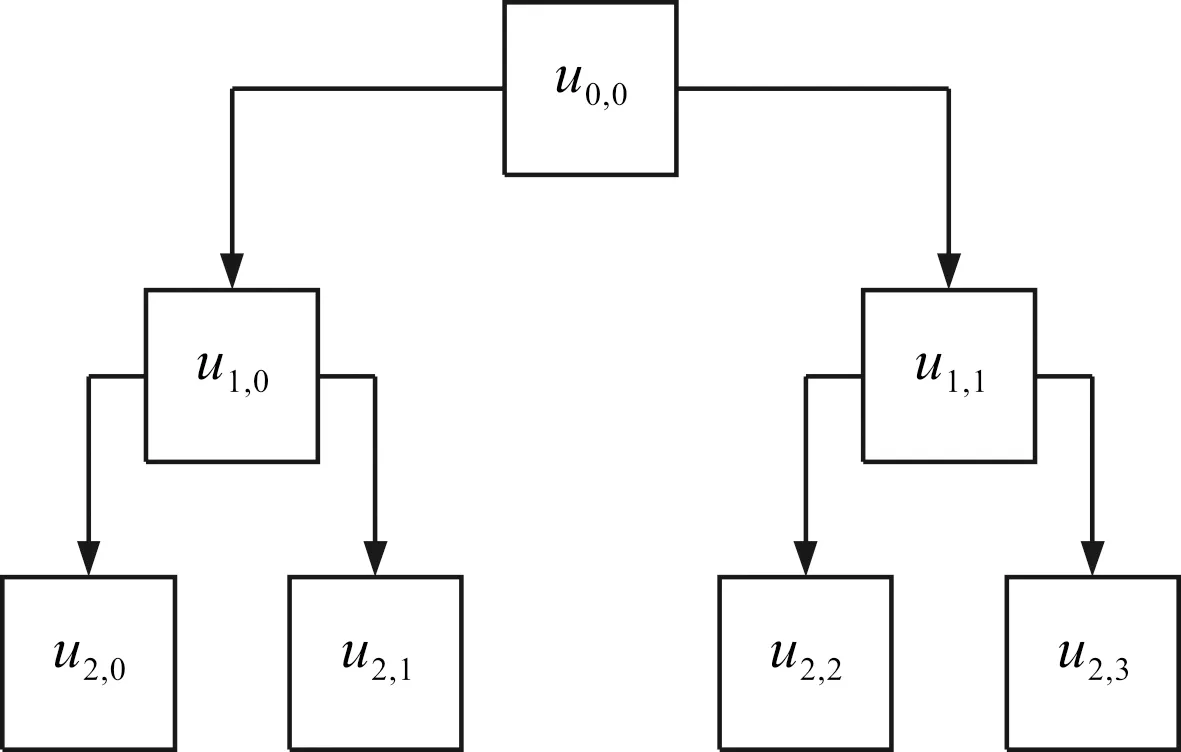
图1 信号u(i)的层次分解示意图

4)计算每个层次分量的加权排列熵,得到2k个层次分量的加权排列熵值,即HWPE定义为:

HWPE(u,k,γ,m,t)=WPE(uk,γ,m,t)

(19)

综上所述,Q0和Q1算子是信号的低频和高频成分,与Haar小波的低通和高通滤波器原理一致;

在图1中最左侧的分解节点u1,0和u2,0的加权排列熵值分布对应于多尺度计算中各尺度的加权排列熵值,也就是分解节点uk,0对应于多尺度计算中各尺度的加权排列熵值。

上述分析说明,多尺度加权排列熵仅分解了信号低频部分的故障信息,遗漏了高频成分的故障信息,而层次加权排列熵在提取信号高频信息的同时,还提取了低频成分的故障信息。

在实际工作中,行星齿轮箱振动信号的高频部分也包含了关键的损伤信息,单一低频成分的信息无法全面表征齿轮箱损伤的固有特性,这证明了对信号进行层次分析的必要性。

1.3 灰狼算法优化支持向量机

1.3.1 灰狼算法

针对支持向量机算法的惩罚系数c和核函数g需要优化的问题,笔者采用灰狼算法进行优化[17]。GWO的种群结构为金字塔形,最上方为α狼,第2层为β狼,第3层为δ狼,最下层ω狼是整个种群的基础。狼群狩猎包含3个阶段,分别是追捕阶段、围猎阶段和攻击阶段。

根据算法生成GWO数学模型,设定t为迭代次数,XP为猎物坐标矩阵,X为种群坐标矩阵,则种群与猎物之间的距离d如下所示:

d=|C·Xp(t)-X(t)|

(20)

种群不断更换坐标,如下所示:

X(t+1)=Xp(t)-A·d

(21)

式中:A,C为系数向量。

A,C可写为:

(22)

式中:r1,r2为范围0到1内的随机数;a为收敛系数。

a可写为:

(23)

式中:Tmax为允许的迭代次数。

狼群抓捕猎物坐标变换如下所示:

(24)

(25)

式中:dα,dβ和dδ为对应α,β和δ狼与猎物的距离;A1,A2,A3和C1,C2,C3为对应于α,β,δ的参数向量;Xα(t),Xβ(t),Xδ(t)为t时刻猎物的详细坐标;X1,X2,X3为对应种群的坐标;Xα,Xβ,Xδ为对应猎物的坐标。

1.3.2 灰狼算法优化支持向量机流程

GWO算法优化支持向量机的流程如下:

1)设置狼种群的规模、允许的迭代次数、优化参数c和g的允许优化范围;

2)随机生成灰狼种群,各灰狼种群的个体坐标包含两个维度,分别是c和g;

3)根据初始给定的参数c和g,对支持向量机进行训练,个体的适应度值由训练样本的诊断准确率来表征;

4)计算每条灰狼的适应度,依据适应度值的大小将灰狼划分为α,β,δ和ω,4个等级,对种群中的每个个体进行坐标更新;

5)若迭代次数超出允许次数,则结束优化,输出最佳的组合参数;否则,继续执行步骤4),直至获得最优的参数。

2 行星齿轮箱故障诊断方法

笔者采用HBA对ICEEMDAN的参数进行优化,并利用具有最佳参数的ICEEMDAN对行星齿轮箱的振动信号进行分解,得到若干个IMF分量,筛选出具有较大相关系数的分量,进行重构;随后,利用HWPE提取重构信号的故障特征;最后,利用GWO-SVM进行故障识别和分类。

基于HBA-ICEEMDAN-HWPE-GWO-SVM的行星齿轮箱故障诊断方法算法的具体流程如下:

1)利用HBA-ICEEMDAN对行星齿轮箱的振动信号进行分解,得到若干个IMF分量;

2)根据相关系数筛选出系数大于0.2的分量,进行重构;

3)利用HWPE提取重构信号的熵值,生成齿轮箱的故障特征样本;

4)利用GWO对支持向量机的参数进行优化,并对特征样本进行训练和测试,输出识别结果,完成故障类型的诊断工作。

基于HBA-ICEEMDAN-HWPE-GWO-SVM的行星齿轮箱故障诊断方法的流程图如图2所示。

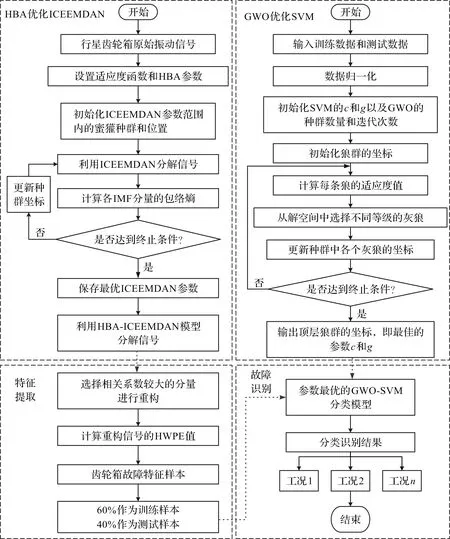
图2 基于HBA-ICEEMDAN-HWPE-GWO-SVM的行星齿轮箱故障诊断方法的流程图

3 故障诊断实验及分析

3.1 实验数据

为了验证基于HBA-ICEEMDAN-HWPE-GWO-SVM的行星齿轮箱故障诊断方法的有效性,笔者利用行星齿轮箱的振动数据进行实验。基于QPZZ-II旋转机械故障模拟实验台进行实验数据的采集,利用该平台能够模拟行星齿轮箱的多种故障形式。

QPZZ-II旋转机械故障模拟实验平台[18]如图3所示。

图3 QPZZ-II型旋转机械故障实验台

齿轮箱实验台的结构配置为:小齿轮齿数为55,大齿轮齿数为75,模数为2 mm。实验模拟了齿轮箱在转速为1 500 r/min下的6种损伤类型。

样本的详细信息如表1所示。

表1 齿轮箱的损伤类型

表1中,6种损伤类型的振动信号由布置在齿轮箱上的加速度传感器进行采集而得到。传感器布置在输入轴电机侧轴承的Y方向;信号的采样频率为5 120 Hz。

笔者选择2 048个数据点为一组样本,每种工况选择45组样本,则共能够获得270组样本;将样本依据6∶4的比例进行分割,得到训练样本和测试样本。

齿轮箱6种损伤振动信号的波形如图4所示。

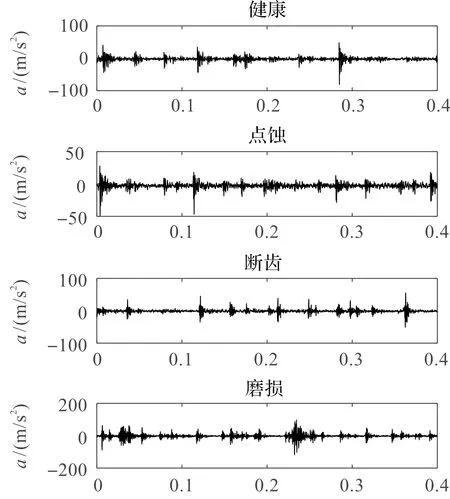
图4 齿轮箱振动信号波形

从图4可以发现:仅通过波形无法直接判断齿轮箱的故障类型,需要采用更加智能的方法进行故障的识别。

3.2 特征提取

3.2.1 HBA-ICEEMDAN分解与信号重构

首先,笔者利用HBA优化ICEEMDAN的2个关键参数。其中,噪声幅值权重的优化范围设置为[0.15,0.6],噪声添加次数的优化范围为[50,600],而筛选迭代次数设置为100次。

为了验证HBA算法在优化中的有效性,笔者利用粒子群算法(particle swarm optimization,PSO)、遗传算法(genetic algorithm,GA)和鲸鱼优化算法(whale optimization algorithm,WOA)进行对比;每种算法的种群规模和迭代次数均为10和30,以局部包络熵最小为适应度函数。

4种算法的优化迭代曲线如图5所示。

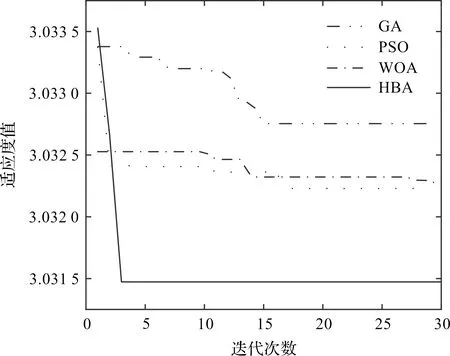
图5 4种算法的适应度迭代曲线

从图5可以发现:在迭代3次后,HBA就达到了最优,而且其最优解优于另外3种算法,证明了HBA在优化过程中的高效和性能。GA最终收敛于一个较大的适应度值,这证明了GA的全局优化性能较差,易陷入局部最优。WOA在迭代过程中未实现收敛目的,证明局部寻优能力较差,无法收敛。

经过优化后,4种算法优化得到的ICEEMDAN最佳参数如表2所示。

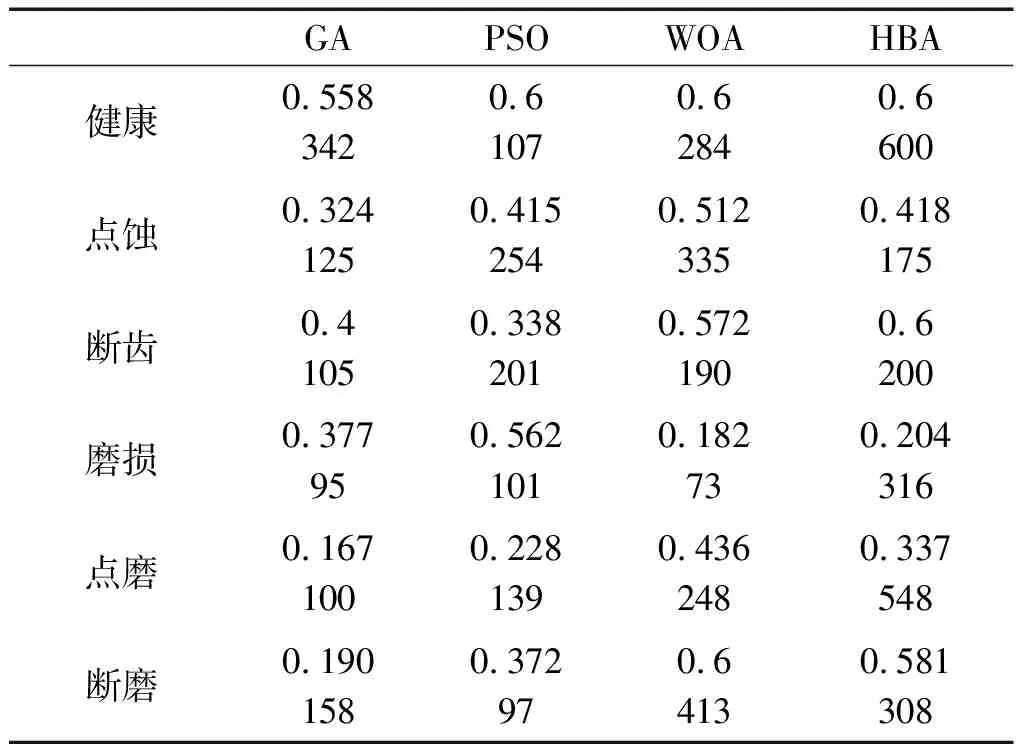
表2 ICEEMDAN最佳参数

笔者将经过HBA优化得到的参数代入至ICEEMDAN中,对齿轮箱振动信号进行分解。

以健康状态信号的分解为例,其分解结果如图6所示。

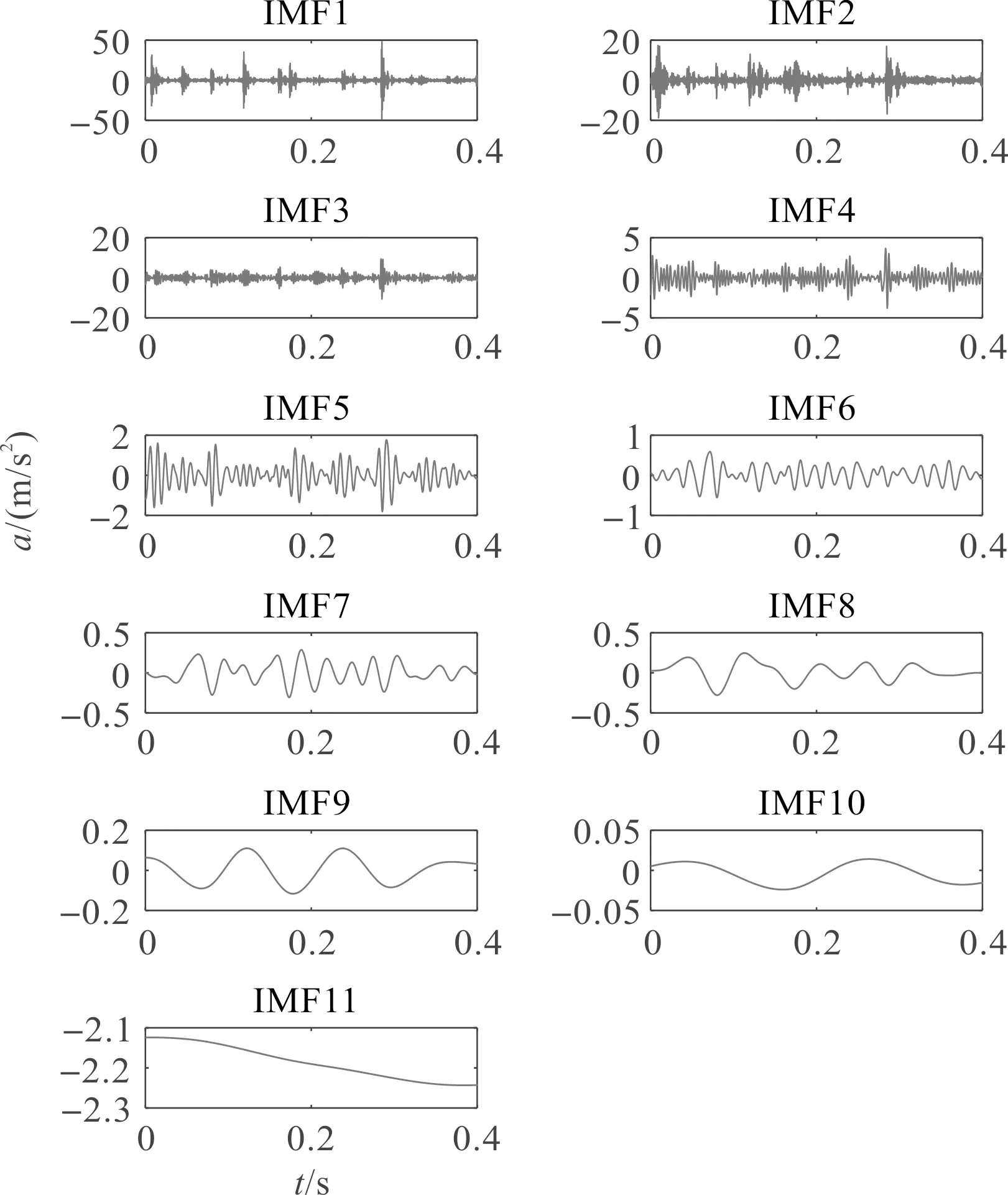
图6 健康样本的HBA-ICEEMDAN分解波形

随后,为了去除信号中的噪声,增强故障特征对齿轮箱工况的敏感性,笔者利用相关系数评估各IMF分量与原始分量的紧密度。

各分量与原始信号的相关程度如图7所示。

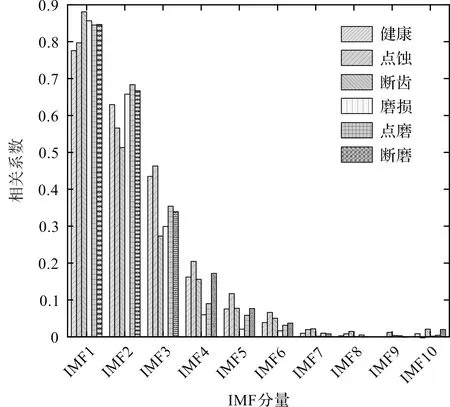
图7 IMF分量的相关系数

从图7可以发现:随着IMF分量阶数的增加,相关系数也随之减小,这证明低阶IMF分量包含了主要的信息。而根据相关系数的相对关系来看,当阶数大于4后,IMF分量的相关系数也比较小,因此,笔者选择前4阶IMF进行重构。

3.2.2 HWPE特征提取

行星齿轮箱的振动信号具有复杂的动态特性,为了准确地表征系统的复杂性,笔者采用HWPE对重构信号进行分析,提取故障特征。HWPE的参数设置为:嵌入维数m=5,时间延迟d=1,分解层数k=3。

首先,为了充分评估不同损伤部位的振动信号差异,笔者利用加权排列熵对6种振动信号进行分析,结果如图8所示。

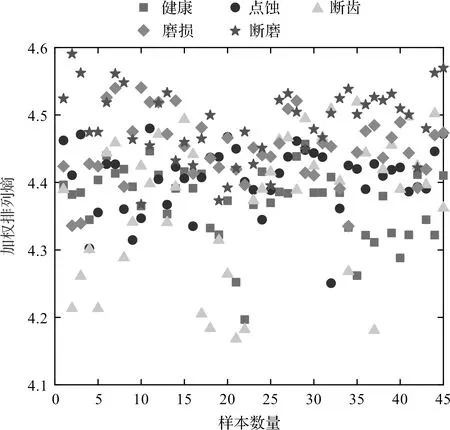
图8 不同工况振动信号的加权排列熵

从图8可以发现:不同工况样本的加权排列熵分布得较为混乱,不具有明显的差异性;但是可以发现点磨样本的熵值普遍较小,这表明信号的复杂度可能较小。这是因为当齿轮正常运转时,振动信号由啮合冲击和环境噪声等相互作用而产生,信号比较不规则;而齿轮发生点磨故障后,信号中出现了周期性较为显著的啮合成分,复杂性降低,因此熵值较小。同时,根据该分析也可证明,对信号进行多尺度分析是有必要性的。

随后,笔者对经HBA-ICEEMDAN分解和重构后的信号进行HWPE分析,得到6种齿轮箱工况在8个尺度下的熵值,如图9所示。

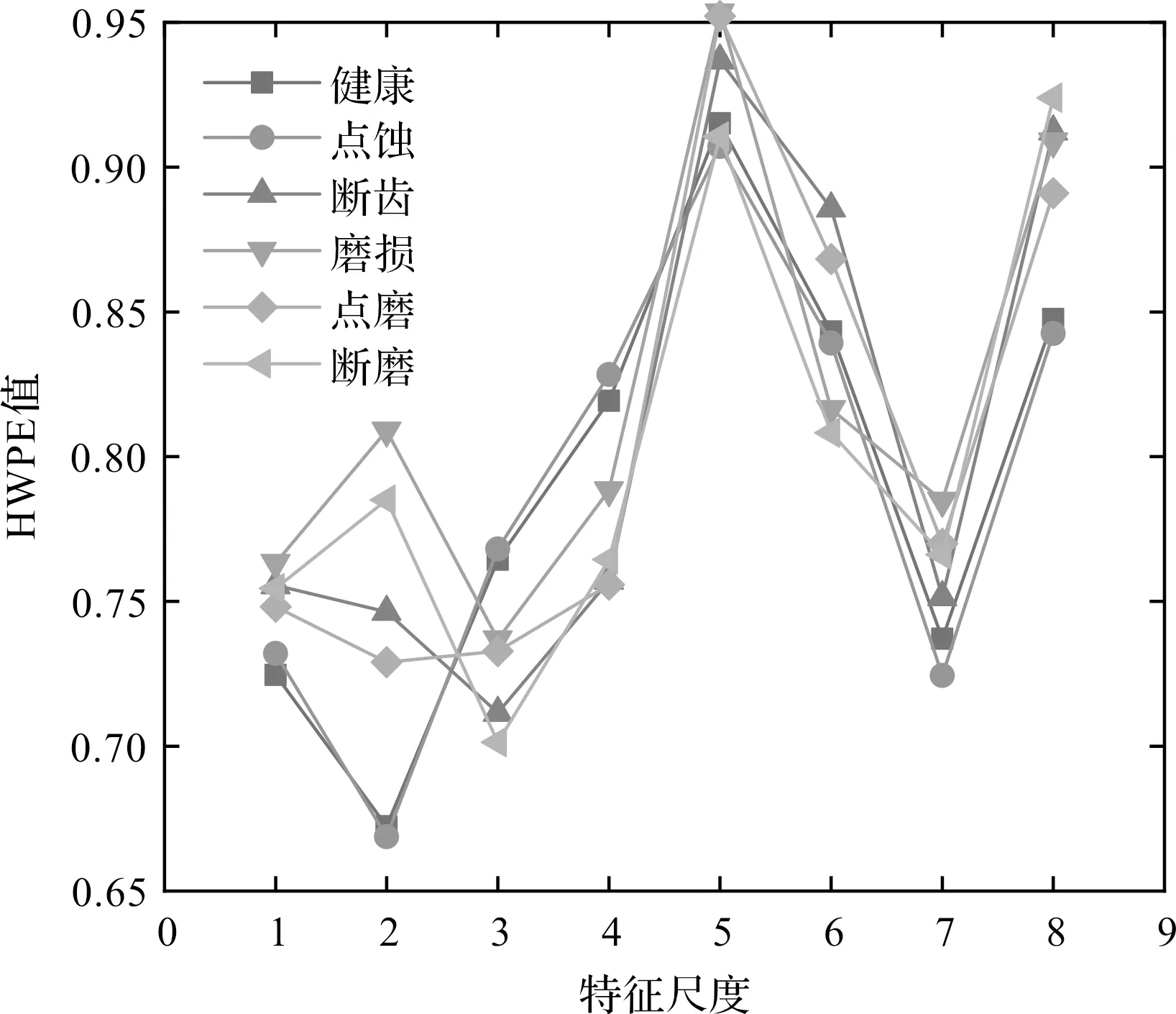
图9 振动信号的HWPE均值

由图9可知:在各个特征尺度上,熵值特征具有一定的差异;但随着尺度的增加,这种差异逐渐减小。

为了增加特征的区分度,提高故障识别的区分度,笔者选择前4个尺度的特征来构造故障特征样本。

3.2.3 模型的诊断

笔者将提取的故障特征按照6∶4的比例随机地分割为训练样本和测试样本,即从每组工况45个样本中,随机抽取27个作为训练样本,18个作为测试样本(总共有135个训练样本,90个测试样本),利用GWO-SVM对其进行故障识别。

测试样本的GWO-SVM分类结果如图10所示。

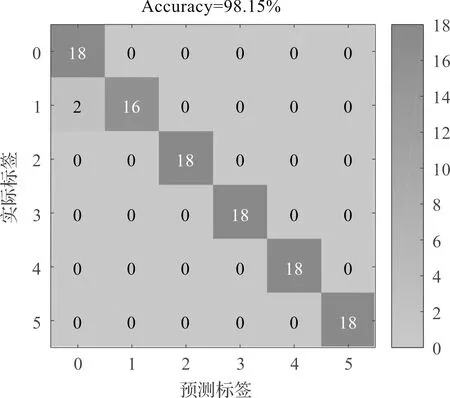
图10 模型的混淆矩阵

从图10可以发现:有5类齿轮箱样本均被准确识别,只有第2类样本(点蚀故障)被错误地识别为第1类样本(健康),准确率为88.89%;在整个测试样本中,被准确识别的样本为106个,被错误识别的样本为2个,总的识别准确率为98.15%。

3.3 模型比较

3.3.1 分类器的优化算法对比

为了研究不同参数寻优算法对模型准确率分类时间的影响,以突出GWO-SVM分类器的有效性,笔者使用遗传算法(GA)、粒子群算法(PSO)、人工鱼群算法(artificial fish school algorithm,AFSA)和蝙蝠算法(bat algorithm,BA)优化SVM的参数,并进行测试样本的识别。

笔者记录了各个分类器的识别准确率和运行时间,实验中,惩罚系数和核函数的优化范围设置为[0.01,100]。

不同分类器的诊断结果如表3所示。

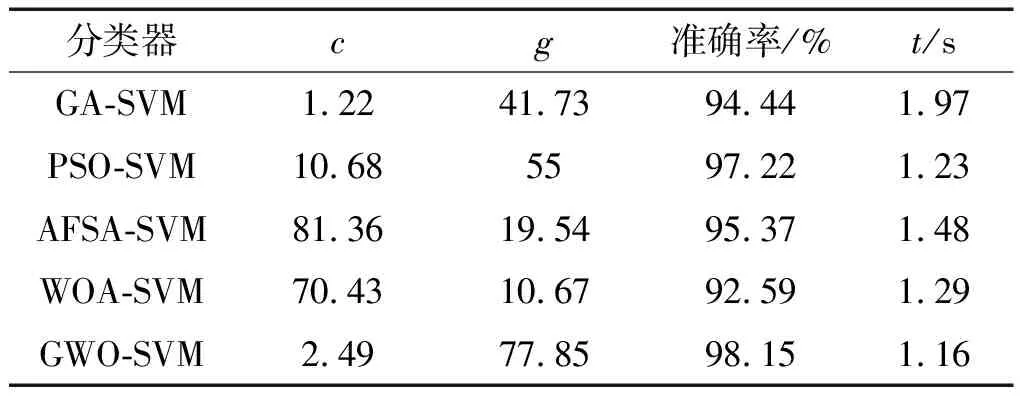
表3 不同分类器的诊断结果

由表3可以发现:各个分类器都能取得超过90%的识别准确率,准确率最低的是BA-SVM,为92.59%;GA-SVM的分类时间最长,需要1.97 s;GWO-SVM的分类准确率最高,为98.15%,分类时间也仅需1.16 s。

根据上述结果可以证明,GWO-SVM在齿轮箱故障识别中具有一定的优越性。

3.3.2 信号分解算法对比

为了证明HBA-ICEEMDAN方法的有效性和优越性,笔者利用GA、PSO、WOA对ICEEMDAN的参数进行优化,并利用HWPE进行特征提取,采用GWO-SVM进行故障识别。此外,为了验证信号去噪的重要性,笔者将原信号输入到故障诊断模型中进行分类,并将结果进行对比。

降噪效果对比结果如图11所示。

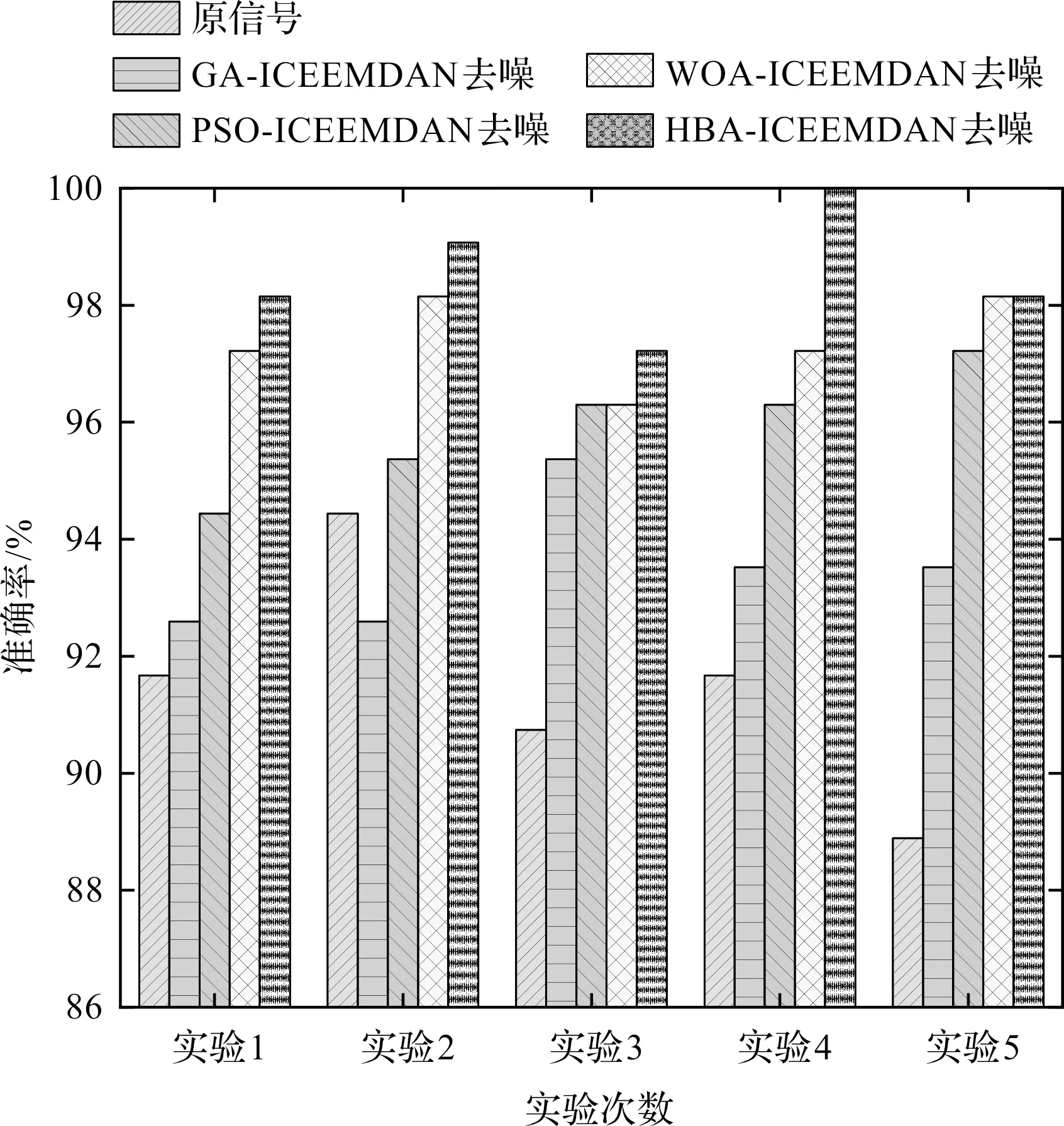
图11 降噪效果对比

从图11可以发现:直接利用原信号进行故障识别的表现最差,这是因为原信号中包含较多的噪声,直接进行特征提取会受到较多的干扰;而就不同信号分解算法而言,HBA-ICEEMDAN的准确率最高,这是因为HBA算法具有较好的全局和局部寻优能力,优化所得到的参数能够使IMF分量质量更高。

基于上述分析,HBA-ICEEMDAN方法能够很好地消除信号中的噪声分量,突出故障特性,以便于后续的特征提取和模式识别。

3.3.3 不同熵值指标对比

为了对比不同熵值指标在特征提取中的有效性和表现,以验证HWPE方法的有效性,笔者分别采用层次排列熵(HPE)、多尺度排列熵(MPE)和多尺度加权排列熵(MWPE)来提取故障特征,结果如图12所示。

图12 齿轮箱振动信号的熵均值

从图12可以发现:各个方法在大多数特征尺度上都能够区分不同的故障类型;但健康和点蚀故障的熵曲线存在重叠和交织现象,区分效果需要进一步评估。

为了更准确地判断HWPE方法的有效性,笔者分别将HWPE、HPE、MPE和MWPE提取的故障特征输入至GWO-SVM分类器中,进行故障的识别,结果如图13所示。

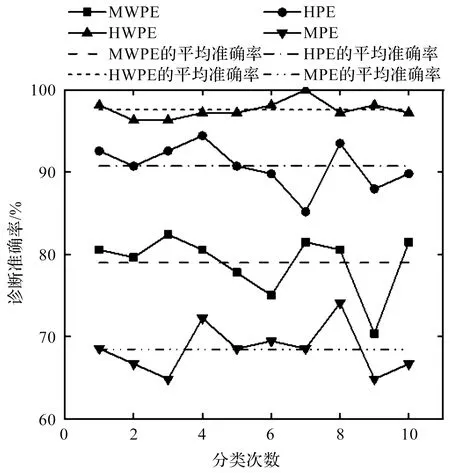
图13 10次分类的平均诊断准确率

从图13可以发现:利用HWPE进行特征提取所获得的准确率最高,其次是HPE,而MPE方法的准确率最低,这证明了利用HWPE进行特征提取的优越性(造成这种现象的原因是因为HWPE和HPE充分提取了重构信号的高频特征,而MWPE和MPE仅提取了重构信号的低频特征,特征提取存在遗漏,因此无法全面地描述齿轮箱的故障特性)。

基于上述分析可知,利用HWPE进行特征提取是有效的,且优于其他对比方法。