双立柱堆垛机立柱挠度模型及其参数优化*
2023-08-31刘文长吴超华陈兴安
刘文长,吴超华,陈兴安
(武汉理工大学 机电工程学院,湖北 武汉 430070)
0 引 言
因具有自动化程度高、作业效率高以及仓储成本低等优点,自动化立体仓库目前得到了广泛的应用[1]。堆垛机是自动化立体仓库中的关键设备,随着自动化立体仓库的不断发展,对其工作效率以及工作性能的要求不断提高[2]。因此,堆垛机的结构设计一直是自动化立体仓库研究的重点。
近年来,在堆垛机结构设计方面,众多学者对其进行了研究,取得了许多有价值的成果。马朝鹏等人[3]对双立柱堆垛机进行了一系列的有限元分析,并对龙门结构进行了优化,使堆垛机整体性能达到了最优;但其网格尺寸需要通过多轮计算试验获得。惠记庄等人[4]建立了堆垛机立柱的动态挠度数学模型及摆动方程,解决了堆垛机立柱在惯性力的作用下产生挠曲变形及摆动的问题;但对立柱的优化问题研究尚浅。杨瑞刚等人[5]采用Kriging模型以及多目标遗传算法(NSGA-II),有效地提高了双高双立柱式堆垛机的静态结构优化设计精度和效率,其模型的建立与算法的求解都相当成功;但最大应力不降反增,优化效果并不显著。袁庆霓等人[6]对不同速度控制方案下的立柱摆动情况进行了研究,分析了堆垛机结构运行过程中的平稳性;但该研究只对比了2种速度控制方案。潘春荣等人[7]对转弯过程中的堆垛机结构进行了有限元分析;但对立柱的优化需要通过改变参数进行反复试验,导致优化结果精度不高、效率极低。吕永峰[8]在目前V型滚轮的研究尚少的情况下,对堆垛机行走机构中V型滚轮接触力与导轨接触刚度进行了分析,其理论模型严谨合理,可以作为工程适用的快捷计算方法,极具价值;但该研究需要不断细化网格以达到容差要求。蒋君侠等人[9]采用变密度法对龙门立柱进行了结构拓扑优化;但优化结果存在较多难以加工的不规则形状,需要进行后处理,极大地降低了优化效率。姚铁斌[10]采用MOGA算法对立柱进行了优化;但其响应面模型严重依赖试验设计,当样本数较小时精度不高,当样本数较大时计算效率降低。另外,赵雨[11]采用遗传算法对立柱进行了轻量化设计,完成了立柱模型的建立和优化;但该设计仅选取了3个变量作为立柱横截面参数。NING Bo等人[12]采用改进的多目标遗传算法对堆垛机参数进行了优化,有效地降低了计算复杂性;但其优化效果并不显著。SHU Yu-feng等人[13]对堆垛机进行了瞬态动力学分析;但其并未给出减少变形量的具体解决方案。WEN Huai-xing等人[14]对小型堆垛机的立柱进行了分析与研究;但其研究只是停留在有限元分析阶段。
在双立柱堆垛机中,立柱为主要的承重结构,且在堆垛机启动和停止时,各部件质量产生的惯性力都会影响立柱顶端挠度[15,16]。但目前存在立柱顶端挠度计算模型精度不高、缺乏立柱参数对立柱顶端挠度影响规律的研究、立柱参数优化方法单一和优化效率不高的问题。
笔者以XHF-B系列1-5T双立柱堆垛机为研究对象,建立新的立柱顶端挠度计算模型和优化模型,并运用粒子群算法对优化模型进行求解,再对优化后的双立柱堆垛机进行有限元分析,最后结合有限元分析结果对理论模型进行验证。
1 双立柱堆垛机及其结构
1.1 双立柱堆垛机简介
双立柱堆垛机结构图如图1所示。
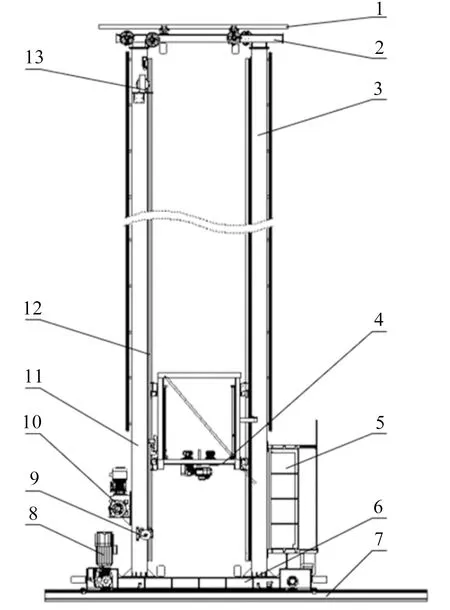
图1 双立柱堆垛机结构图
由图1可知:双立柱堆垛机主要部分为龙门框架(包括上横梁结构、右立柱、下横梁结构以及左立柱)、天轨、地轨、载货台、水平行走机构以及卷扬机。
XHF-B系列1-5T双立柱堆垛机主要参数为:承载货物1 500 kg,载货台质量为500 kg;堆垛机水平行走速度为2 m/s,水平行走加速度为0.3 m/s2;载货台垂直升降速度为0.5 m/s,垂直升降加速度为0.3 m/s2。
1.2 双立柱堆垛机结构分析
双立柱堆垛机为龙门框架式结构,其运行的稳定性以及安全性主要取决于龙门框架的强度和刚度[17]。
在整个龙门框架承受载荷以及惯性力的情况下,高长度的立柱最容易产生应力集中和挠度变形的问题[18]。因此,有必要对立柱进行研究,为堆垛机立柱的设计提供理论依据和参考。
2 立柱挠度计算
2.1 立柱挠度模型建立
双立柱堆垛机零件众多,受力情况复杂,因此,在对立柱进行受力分析时,必须要对其进行简化[19]。首先,双立柱堆垛机的质量较重的部分为上横梁结构、左立柱、右立柱、载货台(包括货物重量)、卷扬机、控制柜、行走电机以及下横梁结构。而行走电机和下横梁结构对立柱的挠度影响较小,因此,笔者认为可以对其忽略不计。
综上所述,双立柱堆垛机质量分布简化图如图2所示。

图2 双立柱堆垛机质量分布简化图
双立柱堆垛机立柱受力情况复杂,尤其在龙门框架式结构下,涉及超静定问题,各个部件相互耦合,难以计算。
目前常用的一种计算模型如下:
当双立柱堆垛机在进行水平运动时,其立柱顶端挠度变形如下式所示:
f=f1+f2+f3
(1)
式中:f1为其他质量惯性力作用下产生的挠度,mm;f2为其他质量弯矩作用下产生的挠度,mm;f3为立柱自重产生的惯性力作用下产生的挠度,mm。
其中:
(2)
(3)
(4)
综上所述,可得:
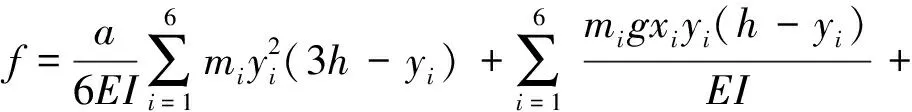
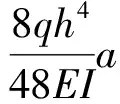
(5)
式中:mi为各部分质量,kg;xi,yi为各部分质心坐标,m;a为水平加速度,m/s2;E为立柱弹性模量,kPa;I为立柱横截面对中性轴的惯性矩,m4;h为立柱高度,m;q为立柱自身均匀分布质量,kg/m。
该计算模型将各部分质量简化为质点,无疑将使得各部分质量过度集中,最终会导致挠度计算结果偏大。
针对该模型的缺点,笔者建立了新的挠度计算模型,新挠度模型示意图如图3所示。
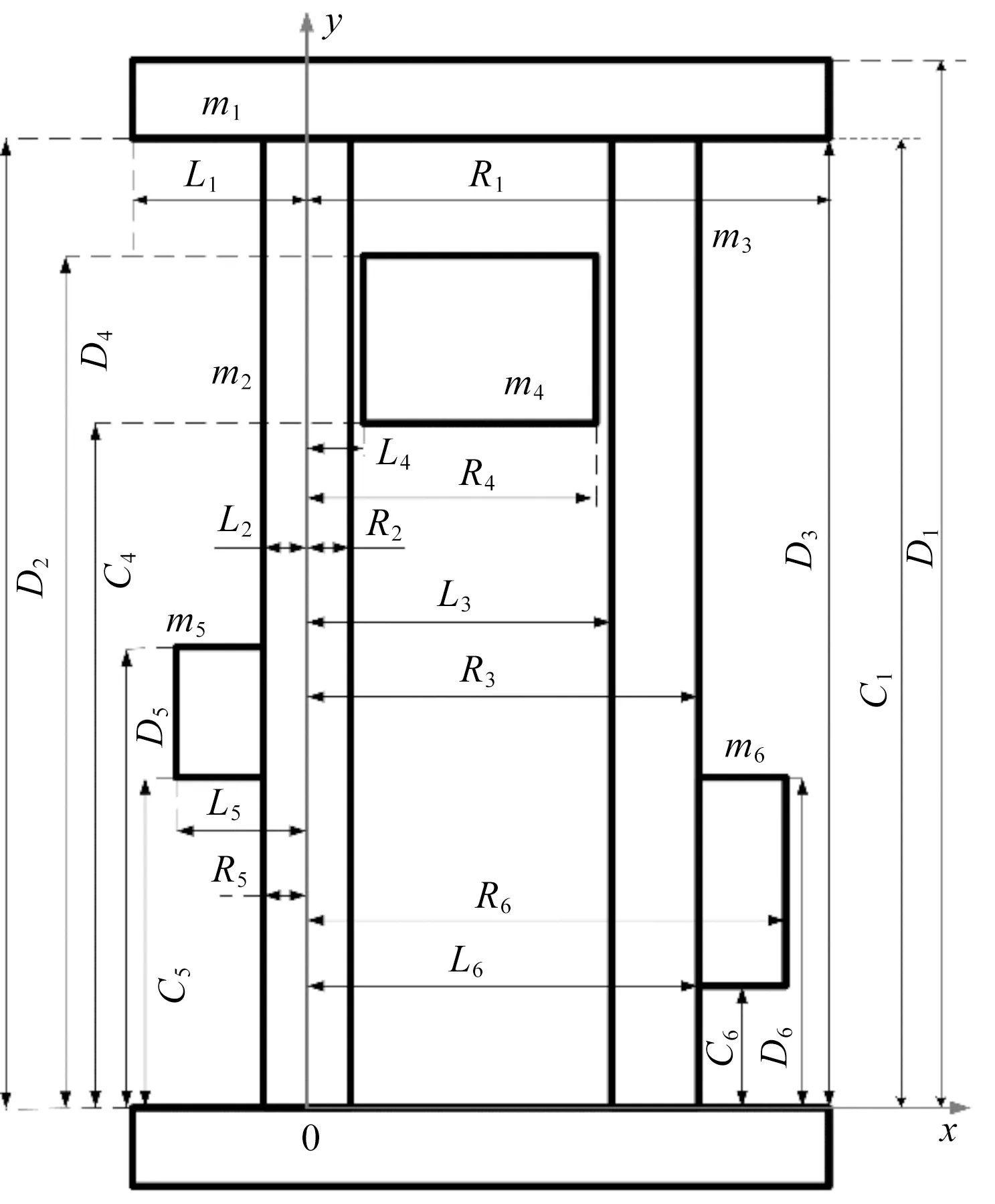
图3 新挠度模型示意图
首先,假设各部分质量为实体(即不空心)时,立柱顶端挠度计算如下:
(6)
(7)
(8)
式中:Li为各部分质量最左端坐标,m;Ri为各部分质量最右端坐标,m;Ci为各部分质量最下端坐标,m;Di为各部分质量最上端坐标,m;ρi为各部分质量的密度,kg/m3;Bi为各部分质量宽度,m(垂直图中xoy平面);a为水平加速度,m/s2;E为立柱弹性模量,kPa;I为立柱横截面对中性轴的惯性矩,m4;h为立柱高度,m;q为立柱自身均匀分布质量,kg/m。
而上横梁结构、左立柱和右立柱并非实体,其横截面示意图如图4所示。
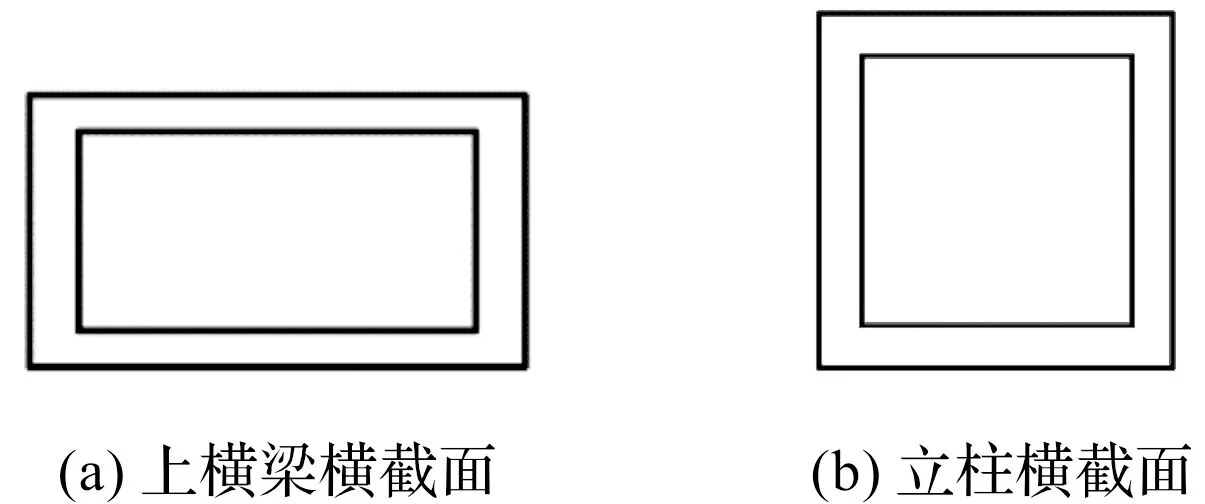
图4 横截面示意图
上横梁结构与左(右)立柱的空心部分示意图如图5所示。
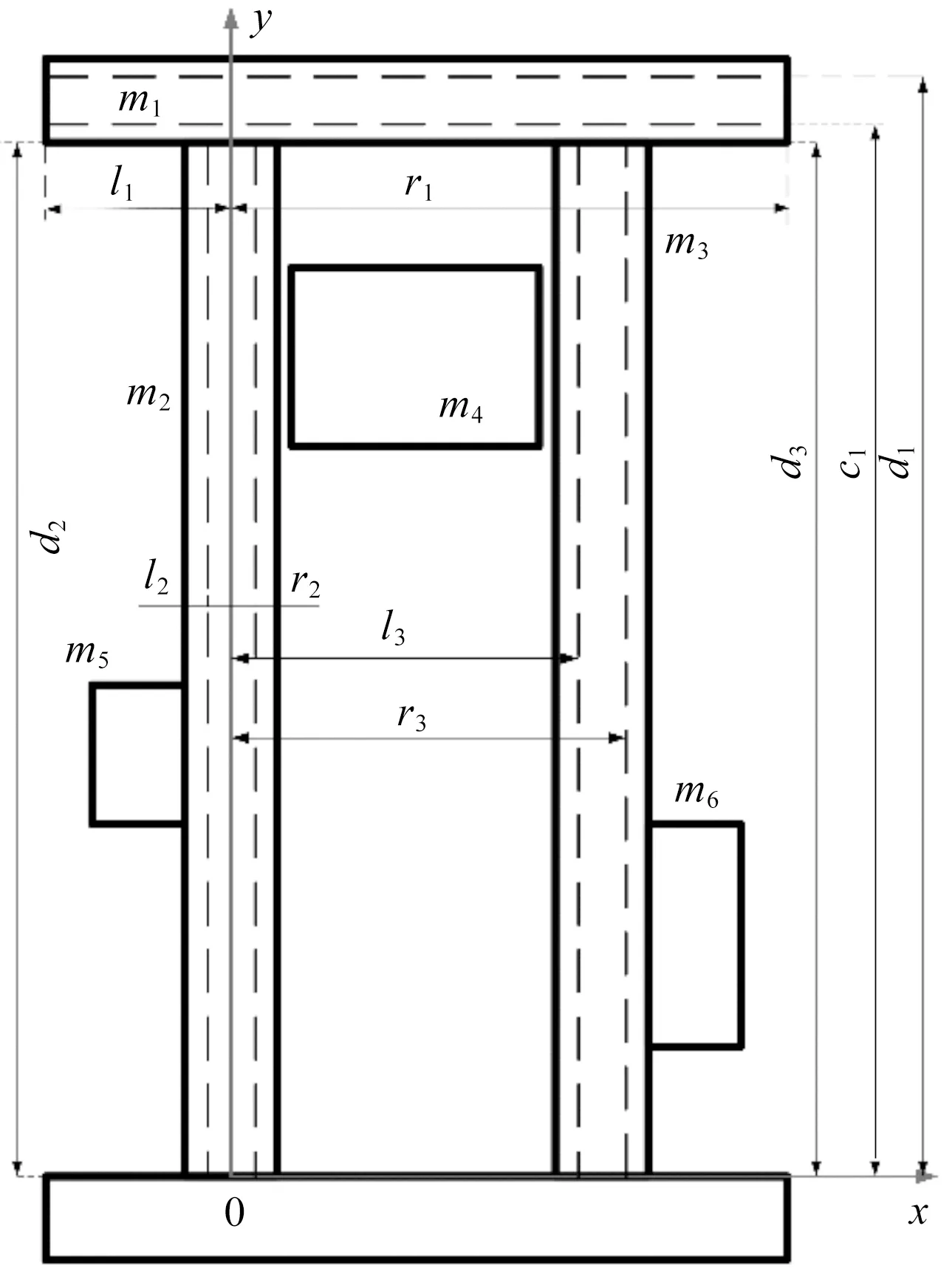
图5 空心部分示意图
由图5可知:空心部分质量对立柱产生的挠度需要被减去。同理,空心部分质量产生的挠度计算如下:
(9)
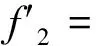

(10)

堆垛机材料选用Q235A,其弹性模量为210 GPa,密度为7 800 kg/m3,泊松比为0.26,屈服极限为235 MPa。但载货台、卷扬机以及控制柜并非只有一种组成材料,如控制柜中含有PLC、变频器、空气开关、继电器以及交流接触器等不同材料的元件。因此,对于载货台、卷扬机以及控制柜这3部分,笔者用其总质量除以总体积得到其平均密度,以其平均密度作为计算数值。
根据堆垛机实际工况,笔者计算得到了载货台、卷扬机以及控制柜的平均密度表,如表1所示。

表1 平均密度表
因此,立柱挠度的计算模型如下:
(11)
该模型引进了微元法,笔者采用积分方式对立柱挠度进行计算,避免了将各部分质量简化为质点而使得挠度计算结果偏大的问题。
并且该模型以平均密度进行计算,充分考虑了部分质量材料不一的问题。
2.2 影响参数分析
在保证立柱高度不变的情况下,影响立柱挠度的立柱参数为立柱的横截面尺寸,即X1、X2、X3以及X4。
立柱横截面尺寸如图6所示。
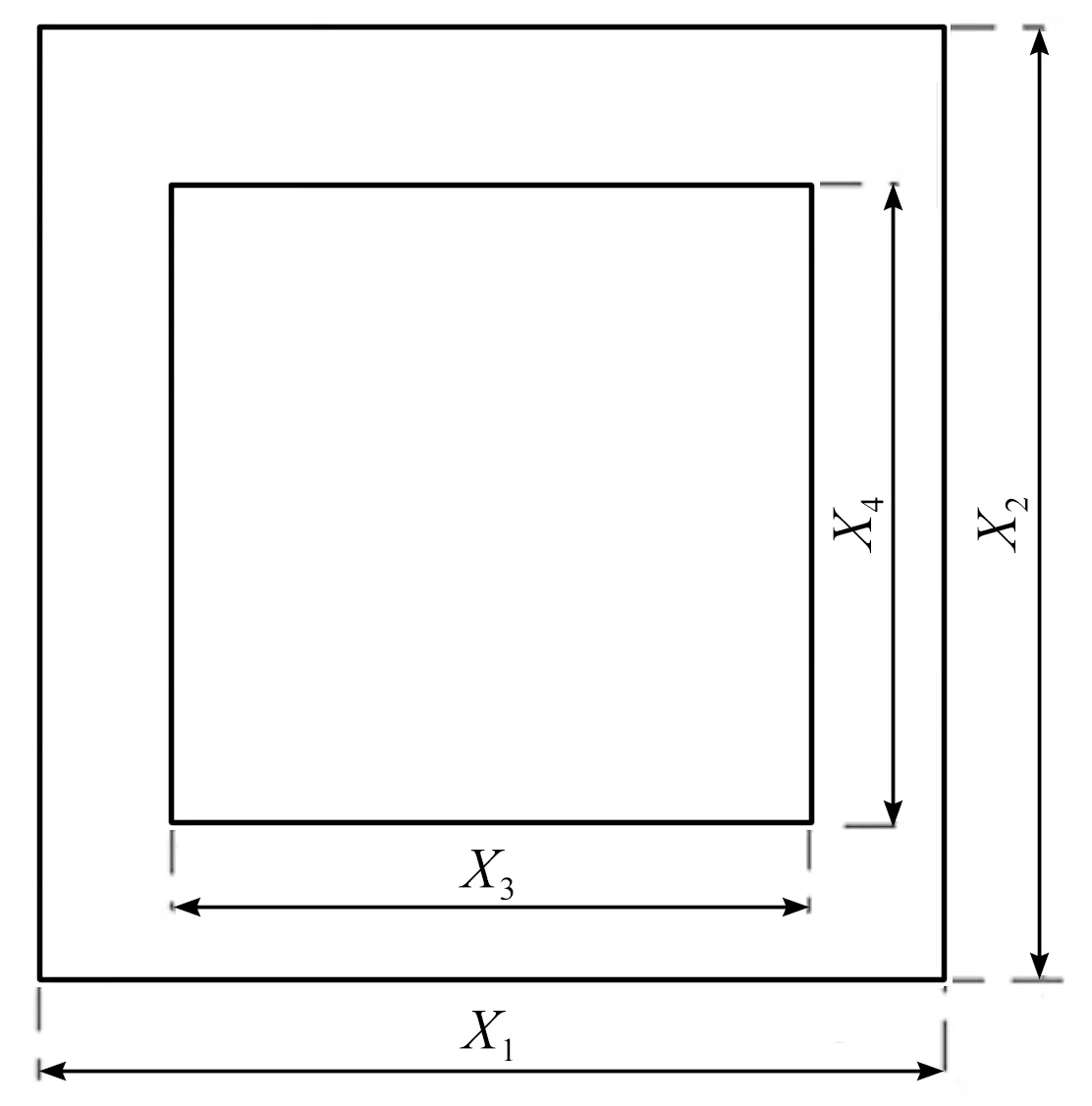
图6 立柱横截面尺寸
立柱横截面尺寸(即X1、X2、X3以及X4)发生变化时,要保证左右立柱中心面的距离始终为J2=2.34 m。
根据笔者所研究的双立柱堆垛机的具体参数,可得到立柱挠度模型的参数表,如表2所示。

表2 立柱挠度模型参数表
由挠度计算式(11)和表2可知:当立柱横截面尺寸(即X1、X2、X3以及X4)发生变化后,与其相关的变量也会发生变化,最终导致立柱挠度发生变化。
研究设计参数对优化目标的影响程度以及影响规律,是进行优化设计的基础,因此,笔者采用控制变量法对立柱挠度模型进行参数影响分析。在改变某一参数时,保证其他参数不变,随后用MATLAB软件绘制出所研究的参数与立柱顶端挠度f之间的示意图。
在改变参数时,应保证立柱壁厚最小为0.005 m,以及参数取值范围为0.3 m~0.6 m。
因此,采用控制变量法时的试验设计参数表如表3所示。

表3 试验设计参数表
根据表3中的试验设计情况得到的影响参数示意图如图7所示。
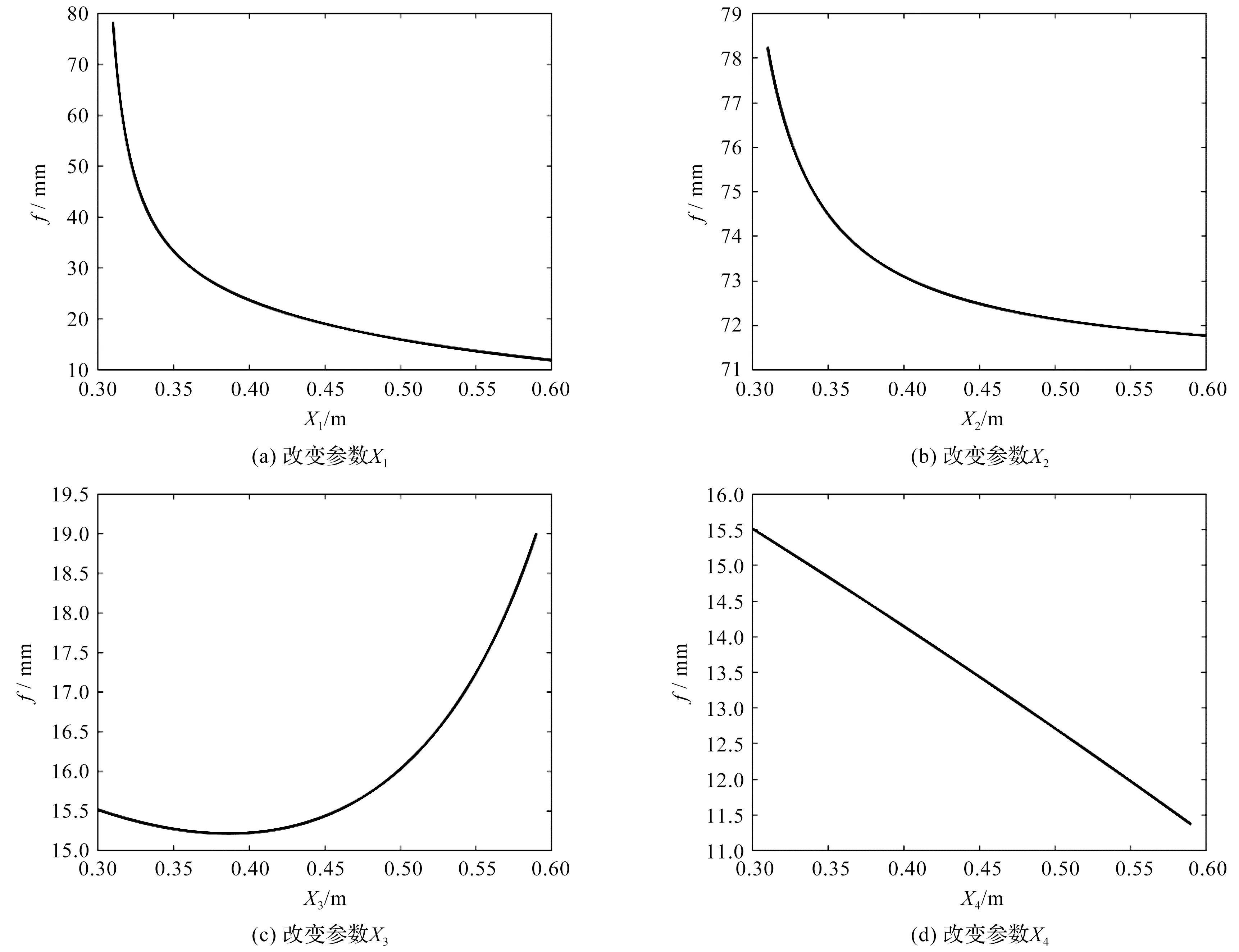
图7 影响参数示意图
由图7(a)可知:当X1增大时,立柱顶端挠度先急剧减小,后缓慢减小。这是因为X1刚开始增大时,惯性矩I增大显著,此时惯性矩I为挠度的主要影响因素;惯性矩I的增大导致f急剧减小。但随着X1继续增大,立柱自身重量变为挠度的主要影响因素;立柱自身重量的增大会导致自重惯性力作用下的挠度增加,最终导致f缓慢减小;
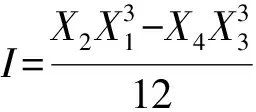
由图7(c)可知:当X3增大时,立柱顶端挠度先缓慢减小,随后越来越大。这是因为X3刚开始增大时,立柱自身重量为挠度的主要影响因素;立柱自身重量的减小会导致自重惯性力作用下的挠度减小,最终导致f缓慢减小。但随着X3的继续增大,惯性矩I减小显著,此时惯性矩I为挠度的主要影响因素;惯性矩I的减小导致f越来越大。
由图7(d)可知:当X4增大时,立柱顶端挠度一直减小。这是因为X4增大时,立柱自身重量的减小一直为挠度的主要影响因素;立柱自身重量的减小会导致自重惯性力作用下的挠度减小,最终导致f减小。
综上所述,由图7可知:参数X1、X2、X3以及X4都为立柱顶端挠度的主要影响参数,且X1、X2的影响程度远大于X3、X4。
3 立柱挠度优化模型建立与求解
3.1 立柱挠度优化模型
双立柱堆垛机初始取值为X1=0.4 m,X2=0.4 m,X3=0.384 m,X4=0.384 m。
此时,双立柱堆垛机初始参数值如表4所示。

表4 堆垛机初始参数值
将表4中参数代入立柱挠度计算模型公式(11)中,可得立柱顶端挠度f为34.230 2 mm。该值远远超过了立柱的许用挠度[f]=H/2 000~H/1 000=(7~14)mm,不满足要求。
立柱作为重要的受力结构,其变形程度的大小严重影响了堆垛机运行的安全性与稳定性。因此,笔者要对立柱进行参数优化,使其满足设计要求。
为保证立柱顶端挠度最小,笔者以立柱顶端挠度最小为优化目标。根据实际工况,立柱横截面尺寸取值范围为0.3 m~0.6 m、壁厚最小为0.005 m。因此,笔者建立的立柱顶端挠度优化模型如下:
0.3≤X1≤0.6,
0.3≤X2≤0.6,
0.3≤X3≤0.6,
0.3≤X4≤0.6,
(12)
3.2 粒子群优化算法
粒子群算法(PSO)是在计算智能领域中一种较为常用的群体智能优化算法[20,21]。在粒子群算法中,每一个粒子都有可能成为最优解,假设共有n个粒子,每一个粒子都在一个D维区域内搜索最优解,对每个粒子的搜索结果进行比较,得到当前的全局最优解。在自身历史最优解和当前全局最优解的影响下,粒子的位置和速度都会发生改变,即调整了搜索方向以及搜索速度,最终通过不断迭代搜索,得到全局最优解[22]。
位置和速度是每一个粒子的重要属性。速度决定了粒子的搜索快慢,位置决定了粒子的搜索方向。其更新公式如下[23]:
(13)
式中:ω为惯性权重,表明粒子在进行下一步更新时受到自身惯性的影响;d的取值为1,2,…,D;i的取值为1,2,…,n;k为当前迭代次数;Vid为粒子的速度;Xid为粒子的位置;Pi为个体极值;Pg为种群的群体极值;c1,c2为加速度因子,其值为正常数;r1,r2为区间[0,1]内的随机数。
为了提高粒子搜索的效率和明确性,一般将粒子的位置和速度限制在一定的区间内。
其次,在原有的粒子群算法中加入自适应变异进行改进[24,25],即在每次迭代中,每一个粒子的数值都有一定的概率会被改变。改进的粒子群算法具有较高的收敛精度和计算速度[26]。
整个粒子群算法流程图如图8所示。
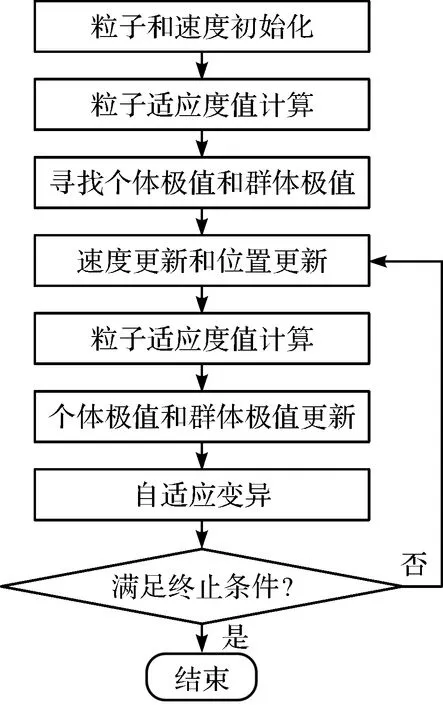
图8 粒子群算法流程图
3.3 结果分析
在粒子群算法中,笔者将粒子群数目设为100,迭代次数为1 000;设置c1和c2为0.5,惯性权重ω=1。
经过计算后得到优化参数以及计算结果为:X1=0.6 m,X2=0.6 m,X3=0.513 m,X4=0.59 m以及f=8.619 9 mm。
笔者将优化结果与初始取值结果进行对比,结果如表5所示。
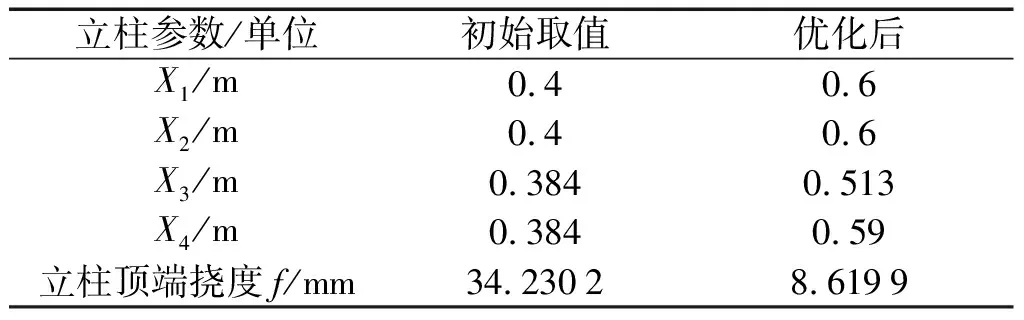
表5 结果分析
由表5可知:经过粒子群算法优化后,立柱顶端挠度降低了74.8%,优化效果显著;
并且优化后立柱顶端挠度为8.619 9 mm,满足立柱的许用挠度[f]=H/2 000~H/1 000=(7~14) mm,符合设计要求。
4 仿真验证
4.1 仿真设置
为验证立柱挠度优化模型是否合理,笔者将立柱参数优化后的双立柱堆垛机模型导入ANSYS Workbench中,进行立柱有限元分析。
上横梁、下横梁以及立柱的材料属性均为Q235A,而卷扬机和控制柜则以其平均密度进行计算。
为使有限元分析符合实际情况并且求解精确,笔者将上横梁、立柱、下横梁、卷扬机以及控制柜之间均设置为bonded接触。笔者采用四面体网格对其进行划分,将过渡方式设置为慢过渡,设受力面局部单元尺寸为1 mm,全局单元尺寸为50 mm,得到节点总数为589 727,单元总数为328 236。
笔者将下横梁左端面设置为固定约束,对右端面限制x,z方向的自由度,对上横梁左、右端面均限制x方向的自由度[27]。
笔者对整个结构添加重力加速度以及y负方向的全局水平加速度,将载货台的重力以及惯性力添加在相应的受力面。
4.2 有限元结果分析
经过有限元分析得到的结构变形云图如图9所示。

图9 结构变形云图
由图9可知:立柱顶端挠度最大,且挠度随着立柱高度的降低而减小。两根立柱在上横梁的作用下,变形几乎一致。立柱顶端挠度仿真结果为9.159 7 mm,与理论计算结果8.619 9 mm的吻合度为[k]=8.619 9/9.159 7=94.1%,满足误差要求,且均满足立柱的许用挠度。
因此,立柱挠度优化模型是合理的,分析方法具有一定的正确性,可为双立柱堆垛机的设计提供理论依据。
5 结束语
笔者采用微元法建立了新的立柱顶端挠度计算模型,然后在此基础上,采用粒子群算法对立柱进行了参数优化,最后通过有限元分析验证了理论模型的正确性。
研究结果表明:
1)优化后的立柱顶端挠度为8.619 9 mm,比初始值降低了74.8%,优化效果显著,且满足立柱许用挠度;
2)在ANSYS Workbench中进行了有限元分析,得到的仿真结果与理论计算结果吻合度为94.1%,均满足立柱许用挠度,即通过仿真验证了理论模型的正确性。
在后续的研究中,笔者将加入轻量化、应力最小等优化目标,并进行相关的实验,从而用工程实例对理论模型的正确性进行验证。
