常微分方程建模案例在教学实践中解决实际问题的探讨与研究

吉莉霞，刘子辉

（盐城幼儿师范高等专科学校，江苏 盐城 224000）

常微分方程在大学数学类专业中属于基础性课程，也是数学分析、高等代数的后继课程[1].在学习常微分方程时，学生很难将其应用在实际生活中，从而使得学生的学习兴趣和积极性不高.在这种背景下，须加强学生的数学建模能力，这样需将常微分方程教学和数学建模思想进行结合，使学生通过计算机提高解决实际问题的能力[2]．常微分方程是研究自然科学、社会科学的基本数学理论和方法，在航空航天、物理化学、金融经济等领域有广泛应用，许多现象都能用微分方程对其规律或原理进行描述[3-5]，例如牛顿万有引力定律、运动定律、能量守恒定律、机械能守恒定律、生态种群竞争、人口发展规律等[6].常微分方程与数学模型、高等代数等课程都有密切的相关性[7]，是大学数学教学当中重要组成部分，常微分方程理论体系严谨，其抽象程度比较高，在讲授时要与实际应用背景相结合，才能更好地实现人才培养目标.

在教学中，选取基础知识进行教学，结合范例内容举一反三，可以帮助学生掌握知识规律.在实际应用中，借助常微分方程范例教学解释现实中的现象，并预测未来的发展趋势，对生产实践、社会生活具有指导意义.

综上所述，本文基于常微分方程数学模型，对其在大学数学教学解决实际问题进行了研究.

1 常微分方程解决实际问题的建模案例

1.1 传染病模型

传染病在人类历史上始终威胁人类的健康，尽管科技不断发展，在一定程度上控制了肆虐全球传染病，然而环境也随着科技的发展而不断恶化，出现一些变异的、新型的传染病毒.传染病的类型差异，会表现出不同的传播过程，对于常微分方程课程教学时，基于一般传播激励构建传染病微分方程模型，转换为数学问题得以解决.

假设Ⅰ：保持总人数不变，用N表示，构建SIR 模型，即用病人、健康者、病愈具有免疫力移出者划分不同的人群，t表示时间，分别用I(t)、S(t)、R(t)标记三类人的比例；

假设Ⅱ：日治愈率用µ表示，病人日接触率用β表示，传染期平均接触数用σ=βµ-1表示.

根据假设Ⅰ，有S(t) +I(t) +r(t) = 1；根据假设Ⅱ，分析移出者、病人改变量，则有，其中dI/dt 表示t 时刻的病人的微分方程，dR/dt 表示t 时刻的病愈者的微分方程，结合初始条件则有公式（1）：

公式（1）的模型为Mc Kendrick、Kermack 的SIR 模型，帮助学生用常微分方程转化实际问题，充分发挥一元微分学知识的作用．通过数学软件Mathematica、Matlab 等进行数值计算、图示、推理，从而将课堂教学效果提高．通过给学生布置一些相关作业，让其通过数学软件、计算机对微分方程进行求解，并对解的实际意义进行分析．例如对于公式（1），利用微积分知识无法将S(t)、I(t)的解析解求出．但可通过Matlab 将相轨线、数值解画出，图1 为SIR 模型的相轨线，图2 为SIR 模型数值解.

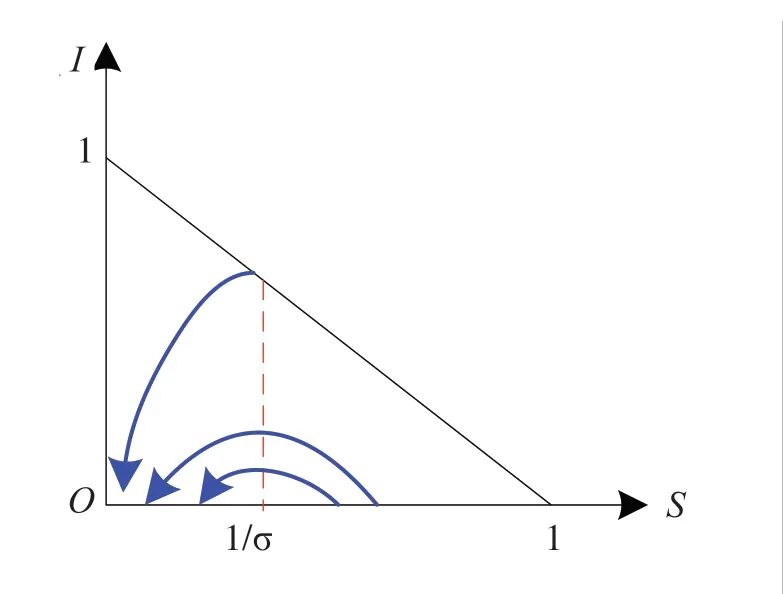
图1 SIR 模型的相轨线图

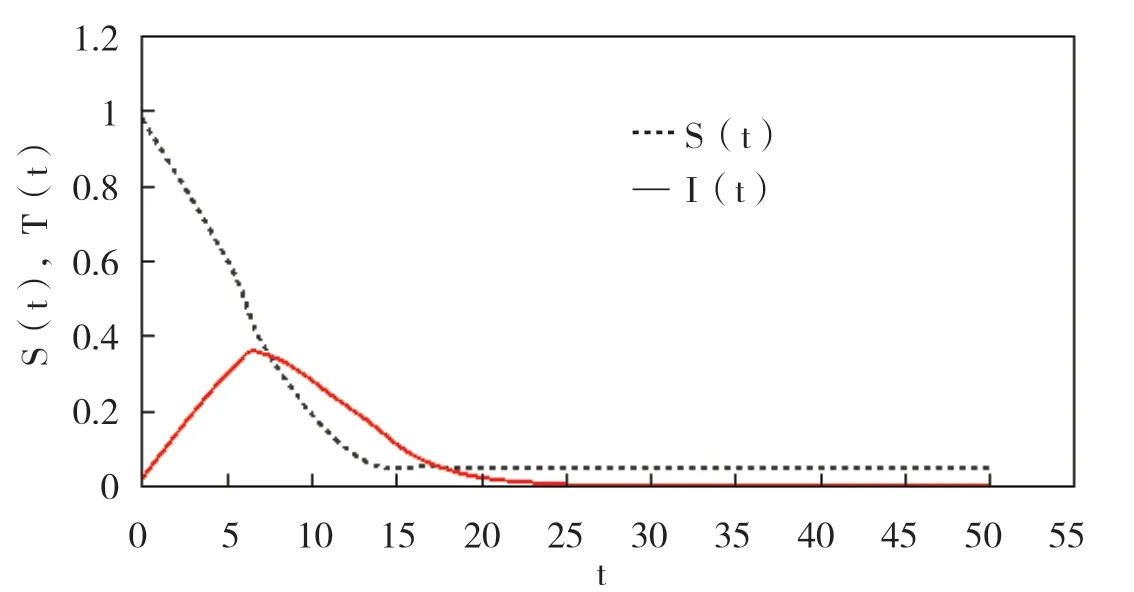
图2 SIR 模型的数值解

通过图形可视化，可将数学问题翻译成实际问题，由图2 知，，即全部病入最终会治愈；时，I(t) 先单调递增，再单调递减为零；若，I(t) 则单调递减为零．所以将会出现阈值，为一个阈值．由σ-1意义知，将卫生医疗水平提高，可使传染病蔓延得到延缓.

1.2 经济调整问题

在数学专业中，高校普遍将金融数学作为重要培养方向．所以，数学建模与金融和经济之间的关联是非常紧密的，且受到社会各界的广泛关注.在研究经济调整问题模型的过程中，要深入讨论经济稳定条件与消费、产值、诱发投资的关联．由于假设投资函数为线性增长函数，因此一般会将线性微分方程模型作为经济调整微分方程模型．但由于实际资源的限制，需修正原有模型，模型修正后为非线性微分方程，此时要基于微分方程稳定性讨论经济稳定条件，模拟修正微分方程的数值[8]．从模型建立、模型修正到理论分析，再进行数值仿真与模拟[9]，激发并培养学生的数学建模思想．对于三部门经济体模型的建立过程中，产值构成为投资、消费、政府购买总和，设定消费为C(t)，实际发生产值为x1(t)，诱发投资为I(t)，政府购买用A表示，通常情况下，政府购买比较稳定，具体见公式（2）：

公式中，投资系数用v表示；k、λ为常数，均大于零．用实际产值增长的线性函数来表示计划诱发投资函数，即计划诱发投资将随着实际产值的增加而增加，这属于线性系统，借助常微分方程知识，可让学生求出产值x1(t)，进一步深入的讨论相关经济学意义．但由于实际资源的限制，此时可启发学生修正模型（3），假设计划诱发投资项为饱和非线性函数，见公式（4）所示：

其中：a为正常数．这时对应的模型变成非线性模型：

采用初等积分法不能直接将解式求出，可引导学生使用稳定性工具、微分方程进行定性分析，通过这个经济学案例，会提高学生学习这部分理论的积极性．对公式（5）中的第二个方程两边进行求导，并将第一个方程代入，得到公式（6）：

公式（6）是二阶常系数非线性常微分方程，基于常微分方程的可转化性，能够将其转化为一阶微分方程组，详见公式（7）所示：

在求解方程组（7）时不适用特征值方法，引导学生在分析平衡点性态时充分融合微分方程定性和稳定性，求出平衡点为系统（7）的唯一解，在处得到一阶近似系统如下：

将系统（8）的对应特征方程的特征根求出，如下所示：

根据常微分方程定性理论，在σ=k+λs-(kλ v a)≥ 0 时，平衡点稳定，因而，当σ2- 4 Δ ＜0，σ＞0 时，稳定焦点为；当σ2- 4Δ ≥ 0，σ＞0 时，稳定结点为；当σ= 0 时，，稳定中心为E( A s , 0 ).

在λ≥ 0 时，需通过政策鼓励将市场边际储蓄倾向s 提高，或将控制投资系数v、边际消费倾向c 减小，这样可确保市场稳定．通过进行经济调整微分方程模型理论分析，引导学生运用数学软件模拟进行数值仿真，激发学生的综合能力，如A=1，k=1/3，a =2，s=1/3，λ= 1/2，v=1/4，此时稳定结点为图3所示的E( 3, 0 ) ；A = 1，k =1/3，λ= 1/2，a = 1/3，v = 1/3，s = 1/3，此时稳定焦点为图4 所示的E( 3,0 )；A = 1，k = 1/3，λ= 1，a = 1，v = 2，s = 1/3，此时稳定中心为图5 所示的E( 3,0 ).

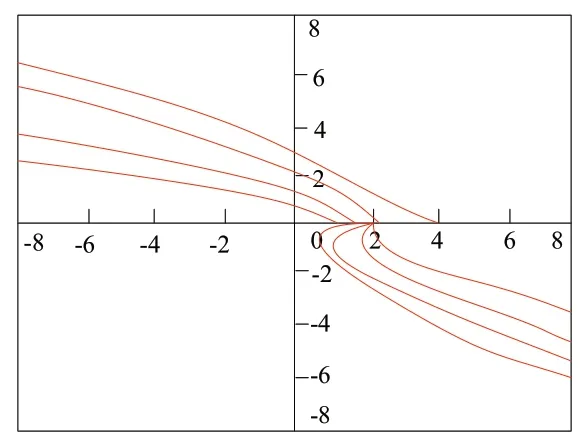
图3 稳定结点数值模拟结果

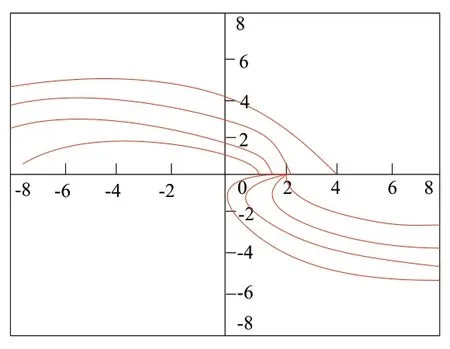
图4 稳定焦点数值模拟结果

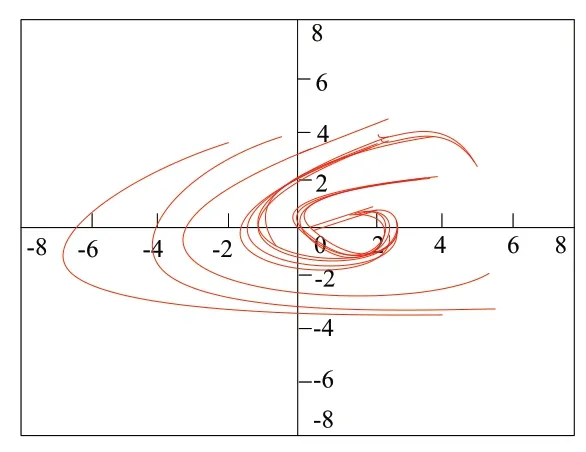
图5 稳定中心数值模拟结果

1.3 废物处理中碰撞问题

在教学中，常微分方程渗透数学建模可通过运用常微分方程基本理论、基本概念、基本方法等体现出来，并用现象解释理论.在进行一些常见微分模型的建构时，可对这些微分模型物理实际进行挖掘[10]，引导学生进行有关微分模型的建构．在教学中，应结合当今时代发展，选择一些激发学生学习兴趣的新颖案例，例如在讲授一阶微分方程应用时，可通过放射性废物处理问题进行分析，美国在进行浓缩放射性废物的处理时，将废物装入密封圆桶，然后放入300 ft 深海里，圆桶虽然非常坚固，但在碰撞海底时可能有破裂发生．圆桶能承受的速度碰撞是问题核心，通过破坏性实验，工程师发现圆桶会在冲撞为40 ft/s 的条件下破裂，随后计算圆桶沉入300 ft 的海底时的末速度．圆桶装满55 加仑放射性废物后，其重量达到W = 538.45 磅，此时其在海水中会受到B = 478.33 磅浮力．海水阻力会在圆桶下沉时发挥作用，大小为D = Cv，C 为常数．相关实验表明C = 0.08.假设垂直向下坐标，以海平面为坐标原点(y = 0)，可得微分方程，其中，D=Cv，dy dt=v，可将上式改写为公式（10）：

公式（10）为一阶线性方程，满足初值条件v(0)=0，其解如下：

计算得到圆桶极限速度如下：

该速度远大于40 ft/s，在进行海底和圆桶碰撞速度v(t)时，须将圆桶下沉时间t求出，但这一点很难做到.因此，下沉深度y的函数用速度v表示，即v(t)=v(y(t))．按照复合函数求导得，将y满足的二阶常微分方程转变为或，且v(0) = 0，y(0) = 0，对两边积分获得公式（12）：

通过数值方法可将v ( 300 )的近似值求出，计算表明，v ( 300 )≈43.2ft/s ＞ 40ft/s，因此，在海中丢放射性废料不安全．目前，美国已改变放射性废料处理方法，禁止在海中抛入放射性废料.在常微分方程课程教学中，融入数学建模思想可达到事半功倍效果.

1.4 计算机病毒传播

计算机病毒成为当今互联网领域巨大安全信息隐患，世界各国都非常重视计算机病毒传播的相关问题，由于会有很多因素对其产生影响、制约，在建立计算机病毒传播数学模型的过程中，需要借助构建微分方程，并进一步分析其传播规律．计算机病毒传播特点类似于生物学中传染病传播过程．计算机病毒传播规模、速度非常惊人，在分析计算机病毒传播问题时，在网络中假设只有一种病毒传播，若系统文件已感染，则其具有免疫力，也就是不会再次被感染；基于上述内容划分网络系统程序：第一类，用S(t)表示并未感染病毒可执行程度，但怀疑计算机感染病毒的数目；第二类，用I(t)表示病毒已经感染计算机的数目；第三类，用R(t)表示病毒对计算机进行感染后，计算机通过杀毒软件程度能偶不再被感染的数目.假设可执行程序的总数在计算机病毒传播期间时稳定的，且为常数N，也就是S(t) +I(t)=N，设定计算机病毒传染率为α，恢复率为β，从而可得到如下微分方程组：

方程组中R(t)和第一个、第二个方程之间没有关联，因而由，可获得，也就是，这属于简单变量分离方程，解为，设定t=t0时，，为初始条件，即，将其代入上式可获得C=I0+S0-ρInS0，方程满足初始条件特解如下：

2 结 语

本文基于常微分方程数学模型，对其在大学数学教学解决实际问题进行了研究，得出如下结论：

（1）分析了常微分方程数学模型在解决传染病模型问题、经济调整问题、废物处理中碰撞问题、计算机病毒传播问题中的应用.

（2）常微分课程教学在选择微分方程建模案例时，会选择与学生实际相结合的方式进行，基于相关常微分方程的知识对问题进行预测或解释.

（3）在教学过程中采取提出问题、分析问题、模型建立、模型求解的案例教学模式，向学生讲清微分方程实际背景，列出微分方程并求解，然后实际现象对生活中的实际问题进行解释，将数学建模思想与常微分方程教学相结合，能够促进学生提高解决实际问题的综合能力，并以更积极的态度探索问题，加深学生对数学建模的进一步认识，从而提高学生的学习兴趣.