正态总体决策曲线参数估计方法及其应用

赵超群 余昊 杨建萍

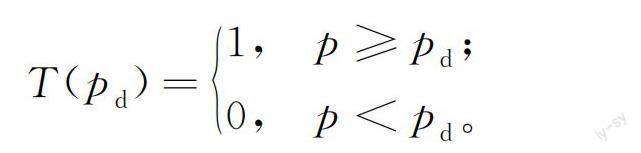
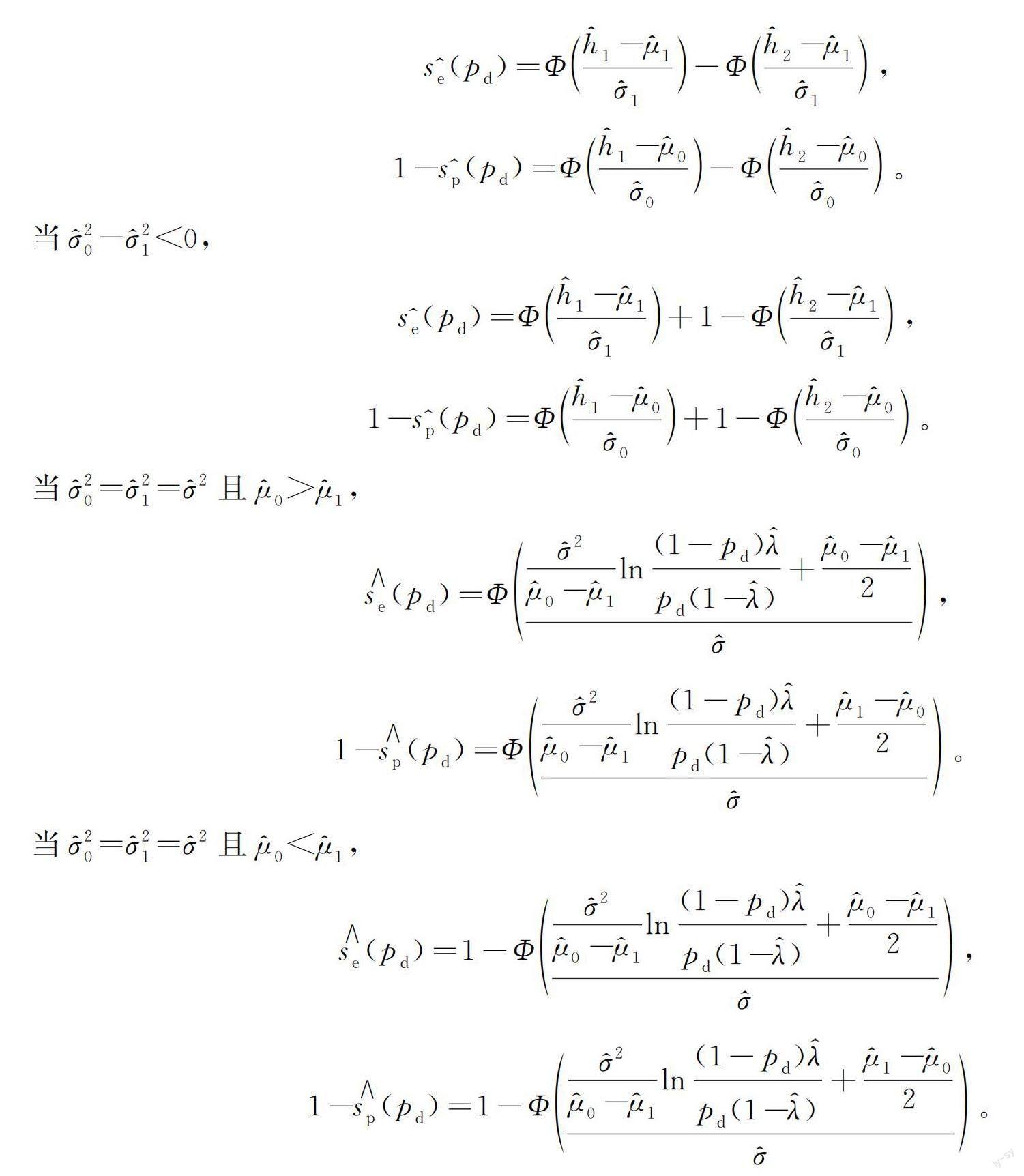
摘 要： 为了给需要平衡收益与风险的决策者提供一种简单有效的风险模型评估方法，提出了一种基于极大似然估计的正态总体决策曲线参数估计方法，并从理论研究、仿真分析和实际应用等三方面研究其特性。首先，从统计理论上对该方法的特性进行了研究，结果表明该方法不仅具有简单易于实践的数学表达式，而且具有相合渐近正态性等良好的统计性质；然后，对该方法在实际应用中的性能进行了仿真，并与现有的非参数估计方法比较，发现该方法在正态总体下具有更高的准确性和可操作性；最后通过实例说明，应用此方法能够有效筛选出乳腺癌的高鉴别性能生物标志物。该研究结果可为决策者评估临床模型和筛选高鉴别性能生物标志物提供参考。

关键词：决策曲线；正态总体；模型评估；收益；参数估计

中图分类号：O212.1

文献标志码：A

文章编号：1673-3851 （2023） 05-0379-09

引文格式：赵超群，余昊，杨建萍. 正态总体决策曲线参数估计方法及其应用［J］. 浙江理工大学学报（自然科学），2023，49（3）：379-387.

Reference Format： ZHAO Chaoqun， YU Hao， YANG Jianping. Parameter estimation of decision curve based on normal population and its applications［J］. Journal of Zhejiang Sci-Tech University，2023，49（3）：379-387.

Parameter estimation of decision curve based on normal population and its applications

ZHAO Chaoqun^a， YU Hao^a， YANG Jianping^b

（a.School of Computer Science and Technology; b.School of Science， Zhejiang Sci-Tech University， Hangzhou 310018， China）

Abstract： In order to provide a simple and effective evaluation method of risk model for decision makers who need to balance benefits and risks， a parameter estimation method of decision curve based on normal population is proposed based on maximum likelihood estimation， and its advantages are also discussed from the three different aspects of theory of statistics， simulated analysis and practical application. First of all， the properties of this method are studied based on the theory of statistics. It is shown that the method not only involves a simple mathematical expression， but it also has some good statistical properties such as consistent  asymptotic normality. Then， the performance of the method in practical application is simulated. Compared with the existing non-parametric estimation methods， it is found that this method has higher accuracy and operability under normal population. Finally， it is demonstrated from examples that this method can effectively screen biomarkers of breast cancer with high differential performance. The research results can provide reference for decision makers to evaluate clinical models and screen biomarkers with high differential performance.

Key words：decision curve; normal population; model evaluation; benefit; parameter estimation

0 引 言

受試者工作特征（Receiver operating characteristic curve，ROC）曲线等传统分类模型评估方法在二分类决策中具有良好的应用价值^［1］。ROC曲线是在测试数据集下，根据不同阈值所得结果，以假阳性率为横坐标、真阳性率为纵坐标画出的图形^［2］。研究人员常通过计算ROC曲线下的面积（Area under curve，AUC）评估分类器的准确率，并通常选择AUC值较大的分类器^［3-4］。类似的分类准确率指标如敏感性、特异性、综合判别改善指数、净重新分类指数和Brier评分等^［5-8］只考虑了诊断测试的准确性，却没有考虑实践中诊断结果带来的收益和潜在风险的关系，这可能导致过度诊断的发生，因此在实践应用中的效果并不理想。

2006年，Vickers等^［9］提出了一种基于决策曲线分析（Decision curve analysis，DCA）的方法，该方法考虑了收益与风险的关系，能有效评估模型、诊断测试和筛选生物标志物^［10］。DCA方法已越来越多地用于评估临床医学研究中诊断测试的准确性和预测模型的价值。Moran等^［11］通过决策曲线研究了乳酸作为脓毒症和脓毒症休克的生物标志物的可行性。Han等^［12］建立了初始原发性肺癌幸存者患第二原发性肺癌的预测模型，并通过DCA方法来评估该模型在临床应用上的价值。Liang等^［13］用DCA方法证实了肝内胆管癌预测模型的分类判别能力。

本文提出了一种正态总体决策曲线参数估计方法。首先，基于极大似然估计得到了该方法关于样本均值与方差的数学表达式，并从统计理论上给出了一些特性；其次，利用R软件对该方法在实际应用中的评估性能进行仿真，并与已有的非参数估计方法进行了性能比较；最后，将这一方法用于筛选高鉴别性能的乳腺癌生物标志物，以说明决策曲线及本文提出的方法在实际应用中的过程和价值。

1 决策曲线分析

DCA方法可以协助临床研究，将临床效用量化为净收益，通过净收益筛选对受试者采取何种治疗措施。D=1和D=0分别表示个体患病和不患病的两种状态，λ=P（D=1）和1-λ=P（D=0）分别表示患病率和未患病率。对于给定个体X，设p=P（D=1|X）为患病概率。阈值p_d∈［0，1］，当p≥p_d时，受试者被判定为阳性，并接受治疗；当pd时受试者被判定为阴性而不接受治疗，将判定的结果用示性函数T（p_d）表示：

设u_kj为对受试者的不同检验结果的效用，其中k∈{0，1}是判定结果，j∈{0，1}是真实的疾病状态。根据期望效用理论^［14］，受试者治疗的期望效用为u₁₁p_d+u₁₀（1-p_d），受试者不进行治疗的期望效用为u₀₁p_d+u₀₀（1-p_d）。当受试者接受诊断测试，得到的阈值与患病概率相同时，即p=p_d，在这个临界值下，将受试者归入患病类别与将受试者归入正常类别的期望效用是相同的，因此可以得到：

结合受试者所有结果的效用，该测试的期望效用可以表示为：

U_A=P（T（p_d）=1|D=1）P（D=1）u₁₁+P（T（p_d）=0|D=1）P（D=1）u₀₁+P（T（p_d）=1|D=0）P（D=0）u₁₀+P（T（p_d）=0|D=0）P（D=1）u₀₀，

不治疗任何受试者的效用可以表示为：

U₀=P（D=1）u₀₁+P（D=0）u₀₀（3）

因而，治疗受试者与不治疗任何受试者比较，该测试的效用是：

U_A-U₀=P（T（p_d）=1|D=1）P（D=1）（u₁₁-u₀₁）+P（T（p_d）=1|D=0）P（D=0）（u₁₀-u₀₀）。

為不失一般性，假设u₁₁-u₀₁=1，得到：

用P（T（p_d）=1|D=1）表示敏感性s_e，P（T（p_d）=1|D=0）表示1-特异性s_p，净收益ф表示U_A-U₀，那么式（4）可以写为：

DCA方法通过不同阈值画出决策曲线，可以用于比较一个模型是否优于另一个模型。两个模型的决策曲线如图1所示，从图1可以看出，模型2的预测效果在阈值范围内具有较高净收益，优于模型1。此外，图1中两条虚线代表两种极端情况，平行于横轴的虚线表示所有样本都是阴性，即净收益为0，“对受试者不做任何治疗”；另一条斜率为负的虚线表示所有样本都是阳性，即“对所有受试者进行治疗”。

2 正态总体下决策曲线参数估计方法推断

假设在某种疾病患病率为λ的人群中，抽取一个样本容量为n的随机样本。令未患病总体X₀～N（μ₀，σ²₀），X₀₁，…，X_0n0为未患病个体样本，n₀为未患病样本数量；患病总体X₁～N（μ₁，σ²₁），X₁₁，…，X_1n1为患病个体样本，n₁为患病样本数量，样本总数n=n₀+n₁。对测试样本X和p用贝叶斯定理可得：

X₀与X₁的概率密度函数之比f₀（x）/f₁（x）为：

二元决策规则将患病概率高于阈值的受试者被判定为接受治疗，所以事件p≥p_d等价于：

为方便计算，不妨假设A=σ²₀-σ²₁，B=μ₀σ²₁-μ₁σ²₀，C=μ²₁σ²₀-μ²₀σ²₁，于是

令h₁和h₂是与μ₀、μ₁、σ₀、σ₁有关的函数：

因此，由式（5）可得，正态总体下，净收益被估计为：

3 仿真分析

本文对正态总体决策曲线参数估计方法进行仿真，利用R软件包Plotrix中的函数对该方法的性能进行评估，并与Sande等^［10］提出的非参数估计方法的准确性进行比较。

为确保研究的可靠性，进行两次不同均值、方差和患病率的仿真实验。另外，设定（n₀，n₁）=（25，25），（50，50），（100，100），（250，250），（500，500），p_d=0.2，0.3，0.4，0.5，0.6，0.7，0.8。第一次仿真中，在X₀～N（3，1.5²）、X₁～N（2，0.2²）的條件下生成1000组λ=0.48的数据，运行得到ф、ф^、标准差、标准误差和非参数估计方法的净收益估计值N_E，结果见表1。ф^在不同样本量和阈值的情况下都接近真实净收益ф；同时，与相同数据下得到N_E相比，正态总体决策曲线参数估计方法得到的ф^比N_E更接近真实净收益。此外，由本文提出的方法得到的净收益标准差和标准误差的平均值较小，说明估计结果准确性较高。

第二次仿真中，在X₀～N（4，5²），X₁～N（0.5，1.2²）的条件下生成1000组λ=0.44的数据，结果见表2。当p_d≥0.5时，N_E与真实净收益值误差较大，ф^误差较小。

通过仿真结果可知，本文提出的方法可以作为评估模型实用性的标准，且比已有的非参数方法准确性更高。

4 应用分析

本文用一个乳腺癌实例来说明本文方法在现实中可用于选取高鉴别能力的生物标志物。乳腺癌是威胁女性健康较严重的恶性肿瘤之一，通常发生在乳腺腺体组织或乳腺导管衬细胞的小叶里，是由乳房细胞变异生长引发的癌症，变异后的细胞相较健康细胞分裂更快，经过积累形成占位或肿块，并且癌细胞可能通过乳房扩散到淋巴结或身体的其他部位。在早期发现这种疾病的时候，乳腺癌的治疗可能非常有效，因此为临床医生提供准确的生物标志物信息来做出治疗决定极为重要。基于DCA方法的效用研究可为乳腺癌的治疗提供必要的依据。

本文选择的数据集来自加州大学欧文分校的机器学习数据库中的威斯康星州预后乳腺癌诊断（Wisconsin Prognostic Breast Cancer，WPBC）数据集^［15］。该数据集中的生物标志物通过乳腺肿块的细针穿刺得到的数字化图像计算得出，生物标志物描述了样本图像中细胞核的形态特征。该数据集收集了198例乳腺癌的患者记录，包含32个生物标志物。前30个生物标志物描述了图像中细胞核的半径、纹理、细胞核周长和紧凑度等特征，最后两个生物标志物是肿瘤的大小和阳性淋巴结的数量。为便于说明，本文使用V1，…，V32来表示这32个生物标志物。

首先进行数据预处理，分别对患病和健康群体的数据进行Shapiro-Wilk检验^［17］。正态性检验显示，WPBC数据集在0.05的显著水平上均未满足正态性假设。为提高正态性，对数据进行Box-Cox转换，转换后的数据再次进行Shapiro-Wilk检验，并删除不符合正态分布的数据。图2是用R软件绘制的数据处理前后的DCA曲线对比图，由图可知，转换后的生物标志物决策曲线净收益显著提高。其次对筛选出的生物标志物结合参数估计方法计算净收益，最后选出6个能显著分类乳腺癌的生物标志物，分别是V2（纹理-平均值）、V7（凹陷度-平均值）、V11（半径-标准差）、V25（平滑度-最大值）、V27（凹点-最大值）和V31（切除肿瘤直径）。使用R软件中的pROC包计算出AUC值排名前10的生物标志物如表3所示。由表3可知，用正态总体决策曲线参数估计方法筛选出的生物标志物与表中的排序不完全吻合。其原因是DCA方法考虑了决策者的偏好，因此在实际应用中AUC评价指标虽然简单但并不能取代DCA方法，AUC注重评价模型的区分度，而DCA方法偏向于评价临床的实用性。

5 结 论

本文提出了一种基于极大似然估计的正态总体决策曲线参数估计方法，能有效地帮助决策者评估模型和筛选生物标志物。通过严密的理论推导，得到该方法的显式表达式仅与正态总体的方差和均值有关且具有相合性、渐近正态性等良好的统计性质。通过仿真计算出估计净收益值与真实净收益值，并且估计净收益值的标准差和标准误差较小，说明该方法具有较高的准确性。此外，该方法应用于筛选乳腺癌生物标志物，结果表明筛选出的生物标志物与通过AUC方法得到的结果不完全吻合，由于本文提出的方法考虑了风险与收益的关系，选取的生物标志物将具有更好的临床诊断效果。

本文提出的是二分类下的决策曲线参数估计方法，对三分类及以上的多元参数估计方法还有待研究。

参考文献：

［1］Pepe M S. The Statistical Evaluation of Medical Tests for Classification and Prediction ［M］. Oxford： Oxford University Press， 2003：28.

［2］Wan S W， Zhang B. Comparing correlated ROC curves for continuous diagnostic tests under density ratio models［J］. Computational Statistics & Data Analysis， 2008， 53（1）：233-245.

［3］Bradley A P. ROC curve equivalence using the Kolmogorov-Smirnov test［J］. Pattern Recognition Letters， 2013， 34（5）：470-475.

［4］Wang S H， Zhang B. Semiparametric empirical likelihood confidence intervals for AUC under a density ratio model［J］. Computational Statistics & Data Analysis， 2014， 70：101-115.

［5］Zhang Z H， Rousson V， Lee W C， et al. Decision curve analysis： a technical note［J］. Annals of Translational Medicine， 2018， 6（15）：308.

［6］Hu B， Palta M， Shao J. Properties of R²statistics for logistic regression［J］. Statistics in Medicine， 2006， 25（8）： 1383-1395.

［7］Leening M J G， Steyerberg E W， van Calster B， et al. Net reclassification improvement and integrated discrimination improvement require calibrated models： relevance from a marker and model perspective［J］. Statistics in Medicine， 2014， 33（19）： 3415-3418.

［8］Pencina M J， D'Agostino R B S， D' Agostino R B Jr， et al. Evaluating the added predictive ability of a new marker： from area under the ROC curve to reclassification and beyond［J］. Statistics in Medicine， 2008， 27（2）： 157-172.

［9］Vickers A J， Elkin E B. Decision curve analysis： a novel method for evaluating prediction models［J］. Medical Decision Making， 2006， 26（6）： 565-574.

［10］Sande S Z， Li J L， D'Agostino R， et al. Statistical inference for decision curve analysis， with applications to cataract diagnosis［J］. Statistics in Medicine， 2020， 39（22）： 2980-3002.

［11］Moran J L， Santamaria J. Reconsidering lactate as a sepsis risk biomarker［J］. PLoS One， 2017， 12（10）： e0185320.

［12］Han S S， Rivera G A， Tammemgi M C， et al. Risk stratification for second primary lung cancer［J］. Journal of Clinical Oncology， 2017， 35（25）： 2893-2899.

［13］Liang W J， Xu L， Yang P， et al. Novel nomogram for preoperative prediction of early recurrence in intrahepatic cholangiocarcinoma［J］. Frontiers in Oncology， 2018， 8： 360.

［14］Vickers A J， Cronin A M， G?nen M. A simple decision analytic solution to the comparison of two binary diagnostic tests［J］. Statistics in Medicine， 2013， 32（11）： 1865-1876.

［15］Mangasarian O L， Street W N， Wolberg W H. Breast cancer diagnosis and prognosis via linear programming［J］. Operations Research， 1995， 43（4）： 570-577.

［16］Street W N， Mangasarian O L， Wolberg W H. An inductive learning approach to prognostic prediction［J］. Machine Learning， 1995， 522-530.

［17］Yang J P， Kuan P F， Li J L. Non-monotone transformation of biomarkers to improve diagnostic and screening accuracy in a DNA methylation study with trichotomous phenotypes［J］. Statistical Methods in Medical Research， 2020， 29（8）： 2360-2389.

（責任编辑：康 锋）