基于自适应正则化光流模型的超声心动图心肌室壁边界识别
2023-08-30张昊童基均吴金玉朱新建刘姗娜张华青
张昊 童基均 吴金玉 朱新建 刘姗娜 张华青


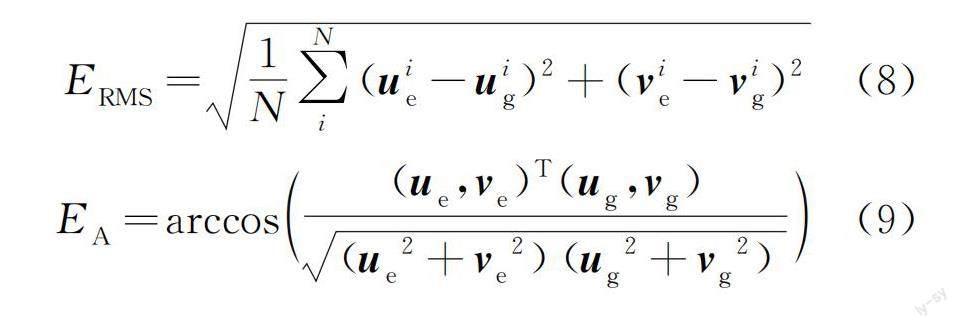
摘 要: 超聲心动图的心肌室壁运动估计是心脏病诊疗的重要技术,但常用的光流模型估计方法采用恒定的正则化平滑系数,识别的室壁边界误差大,运动边界不清晰。针对上述问题,采用自适应正则化光流模型,并将小波分析融入模型,提出了一种超声心动图室壁边界识别的方法。先对相邻两帧图像进行预处理,然后利用Brox光流法对相邻图像进行运动估计得到初始光流矢量,接着光流失量进行二维小波分析得到运动场相对突变的空间分布信息,随后将突变分布信息经过函数映射反馈至光流计算模型中以修正平滑项正则化系数并重新计算光流场,最后重复光流计算过程直到光流场小波高频分量收敛得到最终的计算结果。仿真实验和临床实验的结果表明:该方法的均方根误差和光流角度误差均小于其他方法,平均对比度噪声比高于其他方法,表现出良好的光流计算精度和边界识别能力,可为心脏病临床诊疗提供一种量化评估的手段。
关键词:自适应;正则化;光流模型;超声心动图;心肌室壁;边界识别
中图分类号:TS195.644
文献标志码:A
文章编号:1673-3851 (2023) 05-0293-07
引文格式:张昊,童基均,吴金玉,等. 基于自适应正则化光流模型的超声心动图心肌室壁边界识别[J]. 浙江理工大学学报(自然科学),2023,49(3):293-299.
Reference Format: ZHANG Hao,TONG Jijun, WU Jinyu,et al. Ventricular wall boundary recognition based on adaptive regularized optical flow model in echocardiography[J]. Journal of Zhejiang Sci-Tech University,2023,49(3):293-299.
Ventricular wall boundary recognition based on adaptive regularized optical flow model in echocardiography
ZHANG Hao1, TONG Jijun1, WU Jinyu2, ZHU Xinjian2, LIU Shanna2, ZHANG Huaqing3
(1.School of Computer Science and Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China;2.The Fourth Affiliated Hospital Zhejiang University School of Medicine, Yiwu 322000, China;3.The Second Affiliated Hospital Zhejiang University School of Medicine, Hangzhou 310003, China)
Abstract: Echocardiographic ventricular wall motion estimation is often used in heart disease diagnosis. The common optical flow model estimation method uses a constant regularized smoothing coefficient, which has a large calculation error for the boundary area of the ventricular wall, resulting in unclear motion boundary. To solve the above problems, wavelet analysis was added to the adaptive regularized optical flow model, and a method of echocardiography ventricular wall boundary recognition was proposed. Firstly, two adjacent frames were preprocessed. Secondly, the Brox optical flow method was used to estimate the motion of adjacent images to obtain the initial optical flow vector. Thirdly, the two-dimensional wavelet analysis of the optical flow loss was carried out to obtain the spatial distribution information of the relative mutation of the motion field. In order to correct the regularization coefficient of the smooth term and recalculate the optical flow field, the abrupt distribution information was fed back to the optical flow calculation model through function mapping. Finally, the optical flow calculation process was repeated until the wavelet high-frequency component of the optical flow converges, and the final calculation result was obtained. The results of the simulation experiments and clinical experiments show that the root mean square error and optical flow angle error of this method are smaller than those of other methods, and the average contrast to noise ratio is higher than that of other methods, which proves that this method has good optical flow calculation accuracy and boundary recognition ability, and can provide a quantitative evaluation method for clinical use.
Key words:adaptive; regularization; optical flow model; echocardiography; ventricular wall; boundary identification
0 引 言
目前,超声技术因具有无创、实时、低价格等优势广泛应用于临床[1]。超声心动图可以对患者的生理、心脏功能进行有效显示,还能测定患者左心室的泵血能力,有效诊断二尖瓣反流、左心室壁瘤等心血管疾病[2-3],常被应用于心血管疾病的常规检查以及左心耳闭合、导管支架植入等心脏手术的术中监控[4]。然而,超声心动图作为心血管疾病的诊断技术很大程度上依赖医生的主观判断,可能导致诊断错误[5]。通过心肌室壁运动定量分析可辅助心肌功能评估,给临床医生提供可靠的信息,从而降低潜在风险。但由于超声成像的物理限制,图像中往往存在许多不规则的颗粒状斑点[3];受到散斑、噪声等因素影响,超声心动图中常出现阴影、心肌室壁轮廓不明显等问题,对心肌室壁运动估计带来一定困难。
心肌室壁运动估计的常用方法主要采用光流模型,其原理是利用图像序列中各像素点在时域上的变化计算相邻帧的运动信息,通过2D速度场和灰度之间的关系构建光流求解的约束方程,具有速度快、分辨率高等优势[6-7]。基于匹配、相位等光流法的提出,为光流有效计算奠定了基础;近年来随着深度学习等基于光流思想新方法的提出[8-10],光流法在计算机视觉和目标检测领域得到了更为广泛的应用[11]。光流法具有多尺度、多分辨率等优势,可为超声心动图进行精确的局部运动分析。在光流计算中,为了增加方法的泛化能力,通常引入光流平滑正则项,其作用是解决由于遮挡等因素导致梯度变化过大而产生异常值的问题。但在超声心动图中存在较多散斑和噪声,导致非边界区域梯度信息也很丰富,心肌室壁与周围组织的边界梯度差距较小,因而不能在正则化过程中很好地区分边界与非边界区域,导致光流场的运动边界较为模糊。此外,手工分割心肌室壁边界工作量大且依赖医生的经验。若将边界识别提取到的运动边界信息反馈至光流计算模型中,则有望提高光流计算的准确率,从而提高超声心动图的应用价值。
本文提出了一种基于边界识别的自适应正则化光流模型,并将该模型用于超声心动图心肌室壁边界识别。该光流模型先将经过预处理的相邻两帧超声图像利用Brox光流法进行运动估计,得到初始光流场,再利用小波分析得到心肌室壁与周围组织的运动边界信息,经过函数映射后反馈至光流正则化过程中,建立自适应正则化参数迭代,逐步优化光流计算模型直至小波系数收敛,得到最终计算结果,提高超声心动图心肌室壁边界识别的精度。
1 方法设计
1.1 方法总体流程
本文的设计方法总体流程如图1所示,主要包括图像预处理、初始光流计算、运动边界提取、自适应正则化、光流迭代计算等5部分。整个流程如下:对选择的相邻两帧超声图像进行预处理,以去除噪声;采用Brox光流法进行初始光流计算,得到经过预处理的前后两帧图像光流场;将二维小波分解应用于光流矢量场,提取其运动边界信息;边界信息经过映射加入光流模型的正则化系数中,进行光流迭代计算,得到更新结果;对相邻两次提取得到的小波系数做差,判断平滑系数是否收敛;如未收敛则重复上述过程,直到小波系数收敛,得到最终的运动位移估计结果,以实现超声心动图心肌室壁的边界识别。该方法关键部分是自适应正则化过程,此过程利用提取的运动边界信息构建自适应的正则化系数分布,并用于优化光流模型中的平滑系数。本文采用小波分析提取运动边界信息,反馈至光流正则化过程中。通过小波分析获取的时域和频域的联合分布信息,具有分辨率分析结构和时频局部化的特点[12],通过缩放和移位操作对信号进行多尺度分析,从而提取信号中的有效信息[13]。
1.2 初始光流模型
本文选择Brox光流计算构架作为基本的初始光流模型,利用以下3种假设构建光流计算的能量方程:灰度恒定假设、梯度恒定假设、不连续保持时空平滑约束[14-15]。其中总能量函数由数据项和平滑项组成,数据项包括灰度项和梯度项。灰度项Ecolor如式(1)所示:
梯度项Egradient如式(2)所示:
平滑项Esmooth如式(3)所示:
其中: 為常数;I表示图像序列;x表示像素点的位置向量;w表示像素点x处的位移向量;Δ表示空间梯度算子;γ表示梯度假设和灰度假设之间的权重。
总能量函数是数据项和平滑项的加权和,对总能量函数进行最小化并建立数值化求解方法,以得到前后两帧的运动光流场。总能量函数如式(4)所示:
其中:Egradient和Ecolor相加代表数据项;α为大于零的正则化平滑系数,其表达式如式(5)所示:
其中:αg为全局信息权重,为了弱化散斑的影响,一般设为30;αl为局部信息权重,根据文献[15],一般设为15;Gx、Gy为像素点x在水平、垂直方向上的梯度。
1.3 自适应正则化过程
由于超声心动图中存在的散斑、噪声等现象,心肌非边界区域也会呈现出纹理丰富的现象,梯度差较大。由式(5)可知,正则化系数α与该像素点处的梯度成反比,说明正则化系数α在梯度信息丰富区域系数较小,在梯度较小的区域系数较大,Brox光流法正则化过程并不能很好地区分心肌室壁与周围组织。为解决上述问题,对Brox光流法计算得到的光流矢量进行小波分解提取运动边界信息,并反馈至式(5)中,重新计算光流;重复光流计算过程,直到边界信息收敛,以达到自适应正则化的目的。
1.3.1 运动边界自动提取
利用分割提供的心肌室壁内外模边界信息可以提高超声心动图运动估计质量,为计算相邻两帧的位移提供帮助。本过程利用小波变换自动提取心肌室壁边界的运动信息,小波变换的实质是把信号分解为不同频带的子信号,即将信号分解成位于不同时间和频率上的成分,低频子图成为亮度图像,水平、垂直和对角线高频子图成为细节图像[16]。为解决光流正则化过程中光流场中的运动边界较为模糊问题,将光流运动矢量作为原始信号进行小波分析,可以有效提取心肌室壁与周围组织的边界信息。小波分解方法示意图如图2所示。其中f为原始信号,取最高近似系数fj,其保留了原始信号的各种信息。由fj开始逐级分解为较低近似的近似部分fj-1和小波分量Hcmpt1,即fj=fj-1+Hcmpt1,重复上述步骤,提取出小波分解的4个分量。再将提取出的高频分量Hcmpt4进行函数映射,加入到光流正则化过程中,迭代更新计算光流结果直至小波分量收敛。
取小波分解得到的高频分量,通过映射得到光流估计中的非边界平滑系数Wcmpt,两者关系如表达式(6)所示:
其中:Hcmpt4表示小波高频系数(第四尺度),aw为常量。由于小波系数的极值会因为不同组织间的相对关系而出现正负的差别,故在式(6)中对小波高频系数取绝对值,通过绝对值大小以体现超声图像各组织的平滑程度。
1.3.2 模型正则化过程
本文在正则化系数α2中加入由小波分析得到的平滑系数,利用其提取到的运动边界信息调整心肌室壁与周围组织的边界及它们内部的正则化系数,即减小边界区域的系数和增大非边界区域的系数。加入此项系数后,光流计算中正则项α2如式(7)所示:
其中:Wcmpt为高频分量Hcmpt4经过函数映射得到的平滑系数。用新正则项α2代替α后計算得到的新的光流矢量,对计算结果再进行小波分解,得到新的高频分量Hcmpt4′,并令Hcmpt4′与Hcmpt4矩阵内各元素元素作差,得到差值矩阵,若差值矩阵各元素绝对值的和小于0.01则认为小波系数收敛,否则利用其进行二次映射,得到新的平滑系数Wcmpt2并加入到正则化过程中,得到正则项α3,并再进行下一次光流计算,重复上述步骤直到小波分解得到的高频分量Hcmpt4收敛,即得到最终的位移估计结果。
2 结果与讨论
为了验证本方法的运动边界检测能力和计算精度,使用仿真实验数据及临床数据进行实验。其中仿真实验利用仿真图像模拟心肌收缩运动并提取运动边界信息,以验证提取边界信息的有效性,再以均方根误差和光流角度误差来评价本方法光流计算精度;临床实验中将临床数据分类并进行对比度噪声比实验,验证本方法的运动边界检测能力。
2.1 仿真实验
2.1.1 小波分解
为了仿真心肌运动效果,本文模拟了一个“U”型二值图像,模拟心肌收缩运动,如图3(a)所示。利用固定平滑系数光流法对比计算两帧图像得到初始光流矢量,初始光流矢量再经过二维小波分析,得到4个频率上的小波分量,实验结果如图3(b)—(e)所示,从图中可见,高频分量图3(e)最能反映光流矢量的运动边界信息,且噪声最小。
2.1.2 误差分析
模拟心肌室壁运动计算得到的速度矢量场的精度是衡量运动评估方法优劣的主要指标,可采用均方根误差ERMS和光流向量之间的角度误差EA作为速度矢量场精度的评价指标,计算公式为:
其中:(ue,ve)T表示运动估计得到的光流矢量,(ug,vg)T表示光流矢量的实际值,N表示图像中包含像素点的个数,i表示第i个像素点。ERMS反映了计算得到的速度矢量场与实际矢量场之间的离散程度,EA反映了计算得到的光流向量与实际光流向量之间的夹角误差情况[17]。利用“U”型二值图像,使用仿射技术模拟心肌收缩运动。具体为模拟心肌室壁左侧向右移动2个像素点,心肌室壁右侧向左移动2个像素点,整个心肌室壁向下移动1个像素点,计算范围均取自心肌室壁感兴趣区域。对比计算本文方法和HS光流法、LK光流法及Brox光流法的计算结果精度,以验证本文方法的准确性,所得结果如表1所示。从表1可以看出,本文方法具有较低的均方根误差和光流向量之间的角度误差,这表明本文方法的计算精度更高。
2.2 临床实验
本文采集2021年1月—12月时间段内的45例心血管内科受试者的心脏彩色多普勒超声影像作为实验数据,包含心肌运动异常患者和健康志愿者。所有影像数据均用Philips EPIQ 7C心血管超声成像设备采集,使用X5-1探头,频率为1.0~5.0 MHz。同时,让患者行左侧卧位配合检查,将探头放置于胸前第2到第5肋骨间,观察左室长轴、心尖两腔、心尖四腔和多个左室短轴切面的影像,查看心肌室壁运动是否异常,重点观测左心室两腔心有无运动减弱等情况。根据不同受试者的症状体征,采集受试者左心室不同的超声心动图,选取各实验数据中的两帧以进行光流计算。
为了定量评价运动边界处理光流计算结果,引入对比度噪声比rCN进行分析[18]。本文目的是提取運动边界,使光流计算结果具有更清晰的边界信息,rCN可以很好地反映组织内部的异物检测能力[19],rCN的值越大,则反映本文方法的异物检测性越高。rCN的计算公式为:
其中:μw、μo代表心肌室壁区域内和周围组织的位移均值,δw、δo表示心肌室壁及周围组织的位移标准差。
2.2.1 全局信息权重选择
本文采用小波分析提取运动边界并加入光流正则化过程中,信息权重与该像素点位置的有关,故实际上增加了正则化过程中局部的权重信息。为了减少散斑、噪声影响,确定最佳的全局信息权重αg以减轻超声心动图中散斑、噪声所带来的影响,选取5例健康志愿者数据,截取其心动周期内相邻两帧图像,利用Brox光流法进行对比度噪声比实验。选取αg=1,2,3,…,10分别进行实验,所得结果如表2所示。由表2可知,当全局信息权重αg选择30时,本文方法具有更好的异物检测能力。
2.2.2 对比度噪声比实验
心肌异常患者可大致分为三类心肌异常:心肌室壁运动减弱(心肌室壁收缩的幅度较健康志愿者减弱,即室壁心内膜运动幅度小于5 mm)、心肌室壁运动消失(心肌室壁心内膜运动幅度小于2 mm)、心肌室壁反常运动(心肌左右室壁出现没有同时收缩/舒张状态或节段运动反常)。本文选取另外15例健康志愿者、9例心肌运动减弱患者、9例心肌室壁运动消失患者和7例室壁运动反常患者的实际数据。截取其心动周期内的相邻两帧图像进行实验分析,计算范围取自手动分割的心肌室壁区域及周围组织,实验测试光流正则化过程的迭代速度,结果如图4所示。图4(a)表示手动分割的心肌室壁,图4(b)表示超声成像扇形区域内除心肌室壁外的周围组织,图4(c)表示在光流正则化迭代中,前后两次小波高频分量差值的收敛情况。
对临床分类数据进行对比度噪声比实验,所得结果如表3所示。表3分别表示15例健康志愿者、9例心肌运动减弱患者、9例心肌室壁运动消失患者和7例室壁运动反常患者的平均对比度噪声比。从表3可以看出:相比于其他方法,本文方法具有更高的对比度噪声比,表明本文方法具有更好的边界检测能力,且健康志愿者实验得到的对比度噪声比高于心肌室壁运动异常患者。考虑到健康志愿者和心肌室壁运动减弱和消失的患者之间存在心肌位室壁移量的差异,心肌室壁运动反常患者可能也伴随着不同程度的心肌室壁运动减弱或消失的症状。这表明在心肌室壁运动幅度更大的对象上,本方法的运动边界识别效果更好,即运动边界识别能力与实验对象的心脏泵血能力成正相关。
2.3 方法对比
本文分别利用仿真数据和超声数据进行对比实验,并将实验结果可视化。利用小波分析得到高频分量,并经过函数映射加入到自适应光流正则化过程中,计算得到最终结果,结果如图5所示。由图5可见,相比于Brox光流法,本文方法可以较为明显地提取出心肌室壁和周围组织的运动边界,达到了预期的目标,表明本文方法计算得到的光流场更有效地显示运动边界信息。
3 结 论
在超声心动图心肌室壁运动估计中,由于超声成像的物理限制,超声图像中常出现的散斑、伪影等导致计算得到的光流场运动边界较为模糊,若能提取心肌室壁边界信息反馈至光流计算过程中,改善上述问题,则可以提高超声心动图的应用价值。本文利用小波分析提取运动边界信息,经过函数映射后作为自适应平滑系数,并加入到光流正则化过程中进行迭代计算,使光流计算结果更加准确、边界信息更加丰富。仿真实验验证了本文方法的提取边界信息的有效性及光流计算精度,临床实验验证了本文方法的心肌室壁与周围组织边界的识别能力。
本文方法是在Brox光流法的基础上对光流正则项进行了改进,但其本质还是最小化总能量函数并数值化求解的过程,所以在计算效率上,本文方法较其他光流法没有显著优势。还需要提高算法的效率,以实现心肌室壁运动估计的临床应用。
参考文献:
[1]于潇. 左心室超声心动图降噪和分割方法研究[D]. 哈尔滨: 哈尔滨工业大学,2012:10-11.
[2]江业慧,张平洋,冉红,等. 基于AFI的无室壁运动异常冠心病患者左室心肌运动及其与冠脉狭窄程度间关系的研究[J]. 中国超声医学杂志, 2020, 36(2): 125-128.
[3]向君彦,罗艺,韩小容. 3种超声造影方法评估冠状动脉粥样硬化性心脏病患者室壁运动异常的临床价值[J].检验医学与临床,2018,15(14):2096-2098.
[4]Ge J Y, Chen T S, Ma C Z, et al. Can intracardiac echocardiography completely replace transesophageal echocardiography to guide left atrial appendage closure?:The comparisons of intracardiac echocardiography with transesophageal echocardiography[J]. Journal of Cardiac Surgery, 2022, 37(9): 2766-2775.
[5]Alsharqi M, Woodward W J, Mumith J A, et al. Artificial intelligence and echocardiography[J]. Echo Research and Practice, 2018, 5(4): R115-R125.
[6]Horn B K P, Schunck B G. Determining optical flow[C]∥Proceedings of International Society for Optics and Photonics Conference on Techniques and Applications of Image Understanding. Washington D. C., 1981: 319-331.
[7]Lucas B D , Kanade T . An iterative image registration technique with an application to stereo vision[C]∥Proceedings of the 7th International Joint Conference on Artificial Intelligence. Vancouver, Canada: 1981: 674-679.
[8]Zhang C W, Zhou X D, Zhuge X Y, et al. Learnable optical flow network for radar echo extrapolation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2021,14:1260-1266.
[9]Zhong Y R, Ji P, Wang J Y, et al. Unsupervised deep epipolar flow for stationary or dynamic scenes[C]∥2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, CA, USA:IEEE, 2019:12087-12096.
[10]Shah S T H, Xiang X Z, Ahmed W. Optical flow estimation with convolutional neural nets[J]. Pattern Recognition and Image Analysis,2021,31(4):656-670.
[11]Zheng Y Q, Zhang M F, Lu F. Optical flow in the dark[C]∥2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle, WA, USA: IEEE, 2020: 6748-6756.
[12]Guo T T, Zhang T P, Lim E, et al. A review of wavelet analysis and its applications: challenges and opportunities[J]. IEEE Access, 2022,10:58869-58903.
[13]Wang R, Zhu Q, Bu W C. Multimedia image data compression based on wavelet analysis[J]. Wireless Communications and Mobile Computing, 2022, 2022: 2773868.
[14]Papenberg N, Bruhn A, Brox T, et al. Highly accurate optic flow computation with theoretically justified warping[J]. International Journal of Computer Vision, 2006, 67(2):141-158.
[15]Brox T, Bruhn A, Papenberg N, et al. High accuracy optical flow estimation based on a theory for warping[C]∥Computer Vision-ECCV 2004. Berlin, Heidelberg: Springer, 2004, 4:25-36.
[16]張祥,张达永,张刘辉, 等.数字图像二维多尺度分解与重构小波分析[J].气象水文海洋仪器,2016,33(4):38-41.
[17]Baker S, Scharstein D, Lewis J P, et al. A database and evaluation methodology for optical flow[J]. International Journal of Computer Vision,2011,92(1):1-31.
[18]Shao J H, Wang J R, Zhang Y Z, et al. Subtraction elastography for the evaluation of ablation-induced lesions: a feasibility study[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2009, 56(1): 44-54.
[19]Bilgen M. Target detectability in acoustic elastography[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1999, 46(5): 1128-1133.
(责任编辑:康 锋)
