数学知识与思想方法在高中物理解题中的应用探究

陶德泉

(苏州市田家炳实验高级中学,江苏 苏州 215000)

物理解题是高中生普遍反映的学习难点,提高物理解题能力和解题效率就成为物理教学的重点内容,为此教师应注重引导学生学会综合运用多种途径与方法进行解题.其中数学知识与思想方法在高中物理解题中有着特殊的优势和作用,是解决物理问题的重要和有效方法.同时物理新课标也强调要重视数学工具在物理教学中的运用,因此教师要引导学生学会应用数学知识与思想方法进行物理解题,以此来提高物理解题能力和效率.

1 数学知识与思想方法在物理解题中的作用

数学是物理学习的语言和工具.数学知识与思想方法不但在物理理论知识和实验教学中有着重要作用,在物理解题中更是发挥着独特和重要的作用.

一是能够帮助学生打牢物理解题基础.要提高物理解题能力,需要对物理概念、定理、规律深刻理解全面掌握,而运用数学知识、数学语言和数学思想方法有助于更好地帮助学生理解物理概念、定理、规律等,能够把物理问题抽象成数学问题,降低物理问题理解与解题难度,帮助学生打牢物理解题基础.

二是能够对物理问题进行定性定量分析与计算.数学知识与思想方法能够帮助学生对一些复杂的物理问题进行定性或定量分析,精确计算各物理量之间的关系,理解各物理量之间的关系,使学生更好地理解物理问题的本质,有利于学生正确解题.

三是能够创新高中物理解题思路与方法.借助数学思想方法进行物理解题,能够使学生对复杂物理问题进行转化,使物理解题思维与方法更灵活、更发散、更丰富,有利于消除学生在物理解题中的思维障碍,能够创新物理解题思路方法,从而有利于提高物理解题效率.

2 数学知识在高中物理解题中的应用策略

数学知识在高中物理学习和解题中的应用非常广泛,它涉及多方面的数学知识,主要包括:数轴、坐标系、一次函数、二次函数、三角函数、解析几何、向量、平面与立体几何图形、不等式(组)、数列、圆、概率等数学知识.通过灵活运用运用这些数学知识,就能巧妙解决物理问题.

2.1 二次函数与不等式在物理解题中的应用

例1如图1所示有一质量是m的小铁球系于绳子一端 ,小华握住绳子另一端,让小铁球在竖直平面内做圆周运动.小华握绳子的手距地面高度为d,手与小铁球之间的绳子长度是0.75d.在某次小铁球运动到最低点时,绳子突然断开,小铁球飞行水平距离d后落地,已知重力加速度是g.

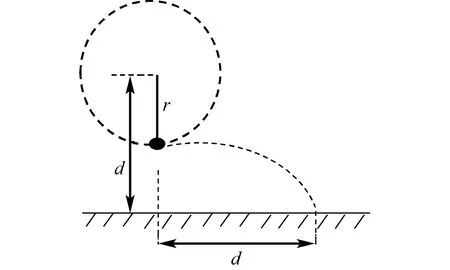
图1 小球圆周运动示意图

(1)求小铁球在圆周最低点时的速度v1是多少?到地面时的速度v2是多少?

(2)求该绳子可承受的最大拉力是多少?

(3)假如在最低点剪断绳子,当绳子多长时小铁球水平平抛距离最大?最大水平平抛距离是多少?

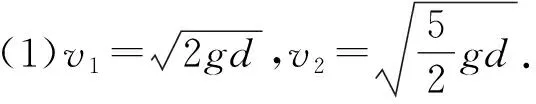
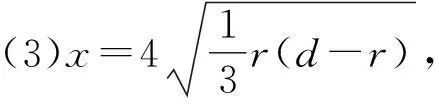
2.2 三角函数知识在物理解题中的应用

例2 在图2中,一个小球从光滑的斜面顶点零初速下滑,斜面底边的长度x保持不变,当斜面的倾角θ是多大时,小球从顶点滑到地面时间最短?

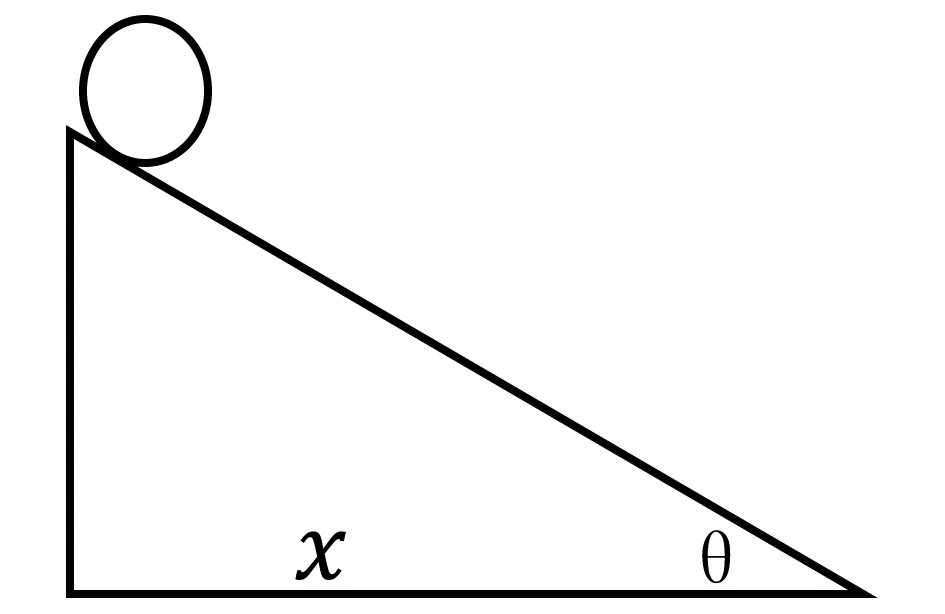
图2 小球斜面运动图

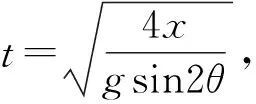
2.3 数列知识在物理解题中的应用

解析18 s 300 m.

在本题求解中,通过运用数学等比数列的通项、求和公式,使该题目容易解决,提高了物理解题效率,也降低了解题难度.

3 数学思想方法在高中物理解题中的应用策略

数学思想方法同样在高中物理学习和解题中的应用非常广泛,它主要涉及转化思想、整体思想、函数与方程思想、数形结合思想、极限思想、数学归纳法、极值法、图像法、微元法、类比法、代换法、数学模型等思想方法.合理巧妙运用上述这些数学思想方法,有利于降低物理解题难度,拓展解题思路与方法,提高物理解题效率.举例如下.

3.1 极限思想在物理解题中的应用

例4 小强利用拖把拖水平的教室地面,拖把头质量是m,拖把头与地面的动摩擦因数是μ,重力加速度为g,小强拖地时沿拖把杆施力且拖把杆与竖立方向夹角是θ,不考虑拖把杆质量.如图3所示.

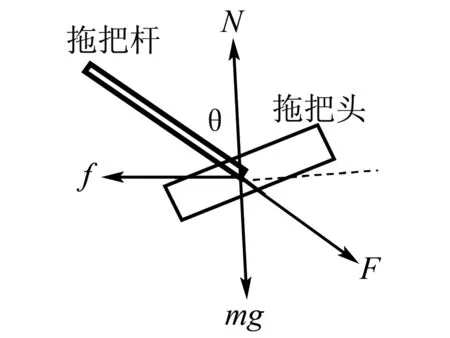
图3 拖把头受力分析图

(1)如果要让拖把头在教室地面上匀速运动,求需要对拖把杆施加多大的力?

(2)假如当拖把刚好从静止开始运动时,其水平推力与此时教室地面对拖把的正压力的比值是a.已知存在一个临界角θ0,当θ≤θ0,则不论小强对拖把杆施加多大的推力,都不能使拖把从静止开始运动,求tanθ0=?

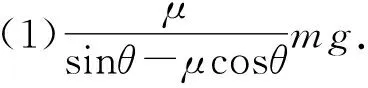
(2)tanθ0=a.

在本问中,就是应用了极限数学思想,抓住临界条件得出θ与a的关系,假设当F无限大时,就可得出临界角的正切值[3].

3.2 数形结合思想(图像法)在物理解题中的应用

例5 一只野兔从地下洞的中心沿直线向外爬出,它出洞的速度v与其距离洞的中心的距离s成反比,当野兔爬出距离洞的中心s1=1 m的P点位置时,其速度v1=20 cm/s,求:当野兔到达距洞的中心s2=2 m的Q点位置时,其速度v2=?从P点到Q所用的时间t=?

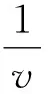
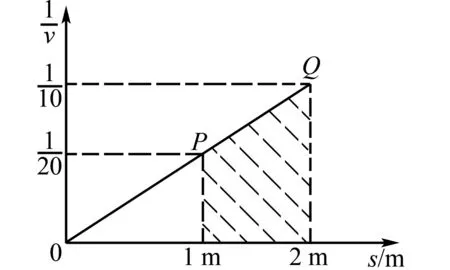
图4 与s图像

通过把物理问题转化成图形或图像,就能形象直观地看出题意或所求结果,而且数形结合思想方法、图像法也是物理解题的常用方法,同时本题目还体现了数学中的转化思想,运用了数学直角坐标的知识等,有利于降低解题难度,提高解题效率[4].

3.3 逆向思维方法在物理解题中的应用

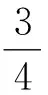
图5 小球斜面滑动示意图

解析t1=t.

通过应用逆向思维方式使解题过程变得很简单,改变了传统解题思维定势,使解题方法得到创新[5].

总之,数学知识与思想方法在高中物理解题中有着独特的优势与作用,既能提高学生物理解题能力与效率,又能培养学生灵活的物理解题思维能力,促进学生物理核心素养发展.因此需要教师和学生充分认识数学知识与思想方法在物理解题中的作用,加强数学知识与思想方法在物理解题中的应用训练,掌握数学知识与思想方法的运用途径与方法,才能有效解决“物理解题难”的问题,提高学生物理学习成绩.