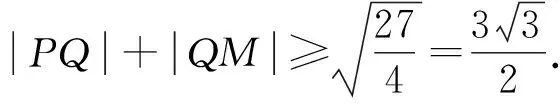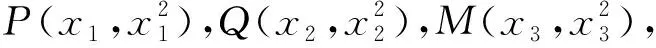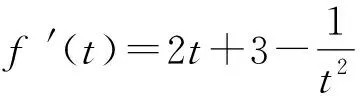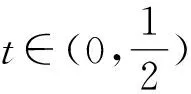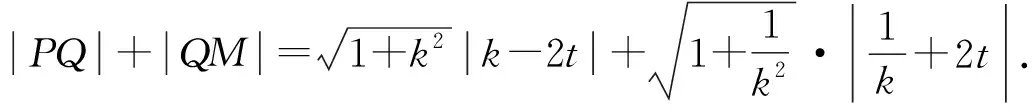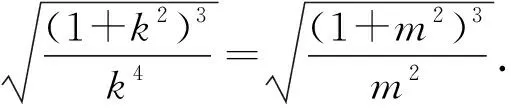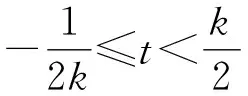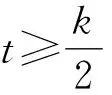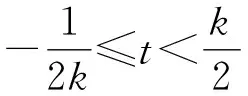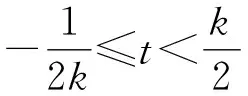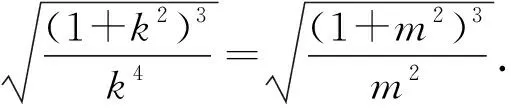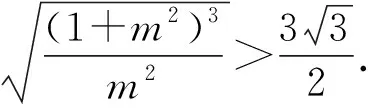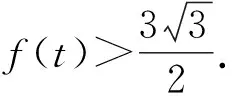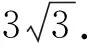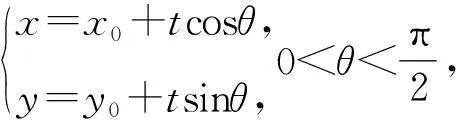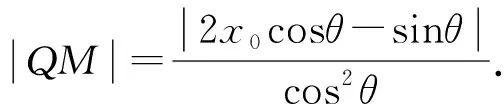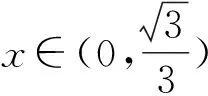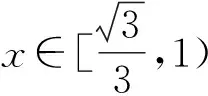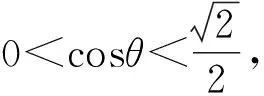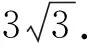2023年新高考Ⅰ卷22题的多解与推广

刘才华

(山东省泰安市宁阳县第一中学,山东 泰安 271400)

2023年新高考数学Ⅰ卷第22题,试题简洁明快,入手容易,深入难,在重视对基础知识、基本方法以及基本思想考查的同时,突出了创新性和理性思维,对学生的数学运算、逻辑推理、直观想象等学科素养均有较高的要求.学生在平时学习过程中要重视教材、回归基础.另外,此试题在反套路和反机械刷题上也起到了很好的示范警示作用.

1 试题呈现

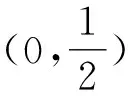
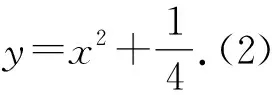
2 试题解析

由于曲线平移不会改变矩形的周长,我们只需证明如下命题:

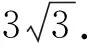
思路1 利用设点坐标的方法和两点间距离公式求出边长,通过放缩化归为一元不等式解答.

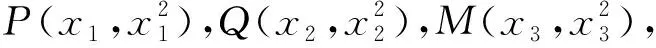
由PQ⊥QM,得

由(x2-x1)(x2-x3)≠0,得

(x2+x1)(x2+x3)=-1.

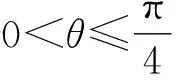
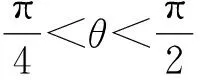
不妨设0

由PQ⊥QM,得

由(x2-x1)(x2-x3)≠0,得

(x2+x1)(x2+x3)=-1.

不妨设0

|x2+x3|≥|x2+x1|.

思路2 利用设点坐标的方法和两点间距离公式求出边长,结合不等式放缩化归为一元函数最值问题,通过导数知识解答.

证法3过程同证法1,得到

思路3利用设直线方程的方法,通过弦长公式求出边长化归为一元不等式解答.

证法4 不妨设P,Q,M三点在抛物线y=x2上.设Q(t,t2),直线QM的方程为y=k(x-t)+t2,且k>0,联立y=x2消去y,得

x2-kx+kt-t2=0.

则Δ=(k-2t)2>0,

由PQ⊥QM,同理可得

(1)当0

(2)当k>1时,

思路4利用设直线方程的方法,通过弦长公式求出边长化归为分段函数,结合一元不等式解答.

证法5过程同证法4,得到

思路5 利用直线的参数方程及其几何意义,化归为三角函数最值问题解答.

t2cos2θ+t(2x0cosθ-sinθ)=0.

由PQ⊥QM,得

故|PQ|+|QM|

令f(x)=x-x3,0

则f′(x)=1-3x2.

作进一步地推广,对于一般的抛物线x2=2py(p>0),我们可以得到如下命题:

命题2可以利用上述证明思路给出不同的证明[1],过程从略.