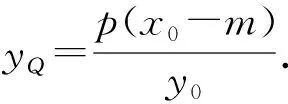圆锥曲线中一类垂直与斜率关系的探讨

高继浩

(四川省名山中学,四川 雅安 625100)

(1)求椭圆E的方程;

(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q,试探究:在x轴上是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.

1 解法探究

视角1 利用判别式求解.

解法1 联立直线l与椭圆的方程,消去y得(4k2+3)x2+8mkx+4m2-12=0.

因为直线l与椭圆有且只有一个公共点P,

故Δ=(8mk)2-4(4k2+3)(4m2-12)=0.

化简,得m2-4k2=3,显然m≠0,于是

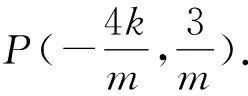
联立x=4与y=kx+m得Q(4,4k+m).

设在x轴上存在定点M(t,0)满足题意,则

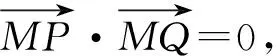
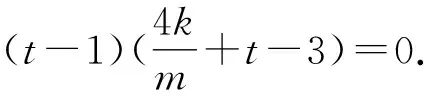
此式对任意实数k,m(m≠0)恒成立,故t=1.所以存在定点M(1,0),使得以PQ为直径的圆恒过点M.

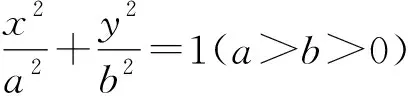
视角2 利用切线结论求解.

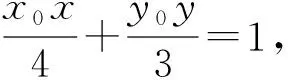
设在x轴上存在定点M(t,0)满足题意,则

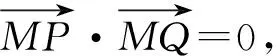
整理,得(t-1)(t-3-x0)=0.

此式对任意实数x0恒成立,故t=1.所以存在定点M(1,0),使得以PQ为直径的圆恒过点M[1].

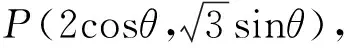
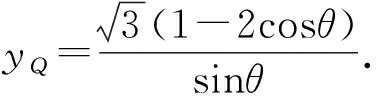
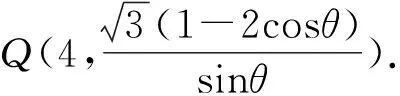
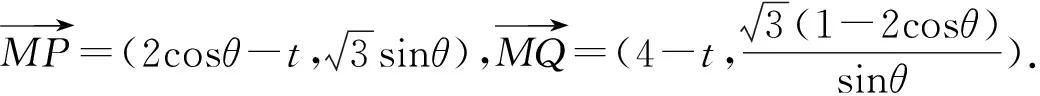
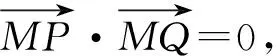
整理,得(t-1)(t-3-2cosθ)=0.

此式对任意θ恒成立,故t=1,所以存在定点M(1,0),使得以PQ为直径的圆恒过点M.

2 拓展探究

试题第(2)问中满足条件的点M恰好是椭圆的右焦点,将其进行拓展可得:

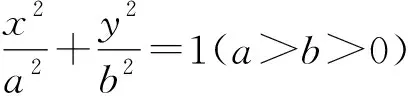
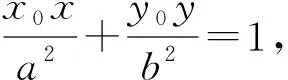
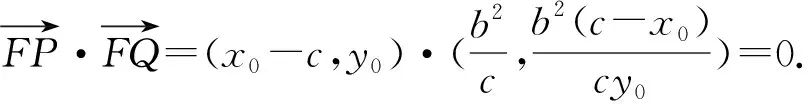
故FP⊥FQ[2].

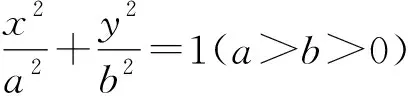
(1)若x0=m,则MP⊥MQ;

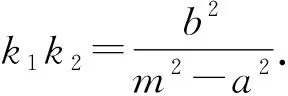
证明显然y0≠0.

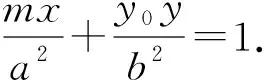
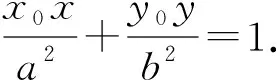
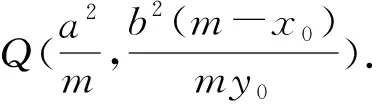
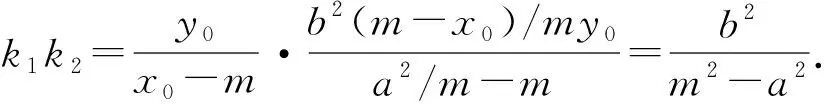
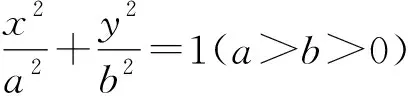
(1)若y0=m,则MP⊥MQ;

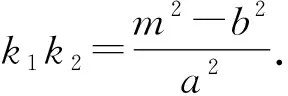
证明显然x0≠0.

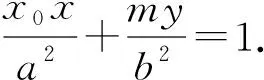
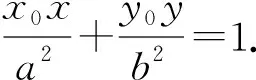
3 类比探究

对双曲线进行探究,得到:

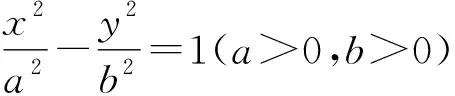
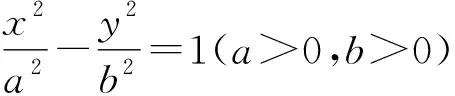
(1)若x0=m,则MP⊥MQ;

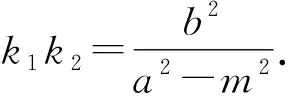
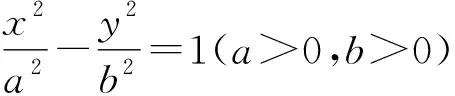
(1)若y0=m,则MP⊥MQ;

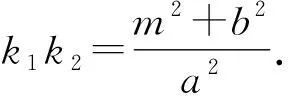
命题4、命题5、命题6的证明与命题1、命题2、命题3类似,略.

对抛物线进行探究,得到:

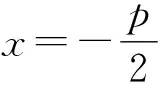
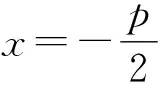
故FP⊥FQ.

命题8 已知抛物线y2=2px(p>0)和点M(m,0)(m≠0),过抛物线上一点P(x0,y0)的切线与直线x=-m相交于点Q.

(1)若x0=m,则MP⊥MQ;

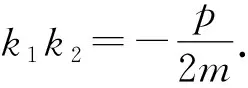
证明显然y0≠0.

(1)若x0=m,则过点P的切线方程为y0y=p(x+m).将x=-m代入解得yQ=0.此时直线MP的斜率不存在,直线MQ的斜率为0,故MP⊥MQ.