基于数学知识内在联系的解题策略探究——以一道几何最值问题的解法为例

李小蛟

(成都市树德中学,四川 成都 610091)

活动是数学教学的基本形式,思考是数学的核心问题.如何提升学生的解题能力,重要的不是研究教师怎样讲,而是研究如何创设良好的问题情境,让学生运用已有经验,在思考与活动中经历“再创造”的过程.通过知识内在的联系将相关知识整合融通,使知识上下沟通、左右逢源,使数学知识系统化、整体化,以达到在头脑中建立完整的认知结构.

1 题目呈现

题目已知菱形ABCD,E为AD中点,且BE=3,则菱形ABCD面积的最大值为____.

题目以平面图形菱形为背景考查面积最值,学生在解题思考时可从平面几何、三角函数、向量相关知识入手,对题目条件进行合理转化.学生在阅读完题目条件后能瞬间联想到相关知识点,看似起点低,但真正动笔演算时却发现解答的落脚点很高,在考场上临场解答非常有难度.下面我们从学生的认知出发,寻找题目条件与相关知识的内在联系,探究本题的解法(为了解题方便,不妨设AB=a,∠EAB=θ).

2 题目探究

探究策略1余弦定理+斜率转化.

题目已知中线长度求面积,学生很自然地联系到利用余弦定理将边角转化,通过菱形的边长和夹角以及中线建立关系,再利用三角形面积公式将面积统一到角度θ.对于分式形式的三角函数最值问题可联系到圆的参数方程(三角代换),将三角函数问题转化为解析几何问题中的斜率.

评注几何问题代数化处理是数学解题中一贯的基本思想方法,求解面积最值转化为代数最值,再联系三角函数与解析几何的内在联系,最后将问题转化为解析几何中的斜率问题.

探究策略2余弦定理+辅助角公式.

同探究策略1将面积转化为三角函数求最值后,可采用变更主元的方法(本题将θ看成常值,将S看成变量),利用辅助角公式变形,再利用正弦函数本身的有界性求解.

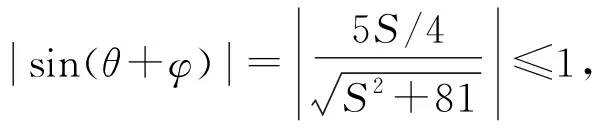
评注利用三角函数的有界性是求解最值(范围)问题最有效的一种策略,探究策略2利用三角函数自身内在的性质将求解问题简单化,强化知识本身具体的属性,重视知识本源,强化深度学习[1].

探究策略3 余弦定理+万能公式.

同探究策略1将面积转化为三角函数求最值后,出现两个变量(sinθ,cosθ),如何将双变量问题转化为单变量问题是解答中最关键的思考点,而万能公式是将正余弦函数统一到同一函数名(正切函数)最有效的方法之一.

所以(SABCD)max=12.

评注三角函数的最值(范围)问题求解是要将三角函数化为三个一“同一角度、同一函数名、一次式”进行求解.探究策略3还引导将非齐次的分式形式转化为基本不等式或对勾函数求解最值.

探究策略4 阿波罗尼斯圆.

将动点转化为定性的点轨迹(或将变量转化为定量)是研究平面几何的有效方法.基于本题中菱形所有边长相等,点E又为边AD的中点,于是可联系两线段比值为定值的阿波罗尼斯圆来解决问题.

在直线BE上取两点M,N,使得BM=2ME,BN=2BE,取MN中点O则点A轨迹是以O为圆心,ON为半径的圆.

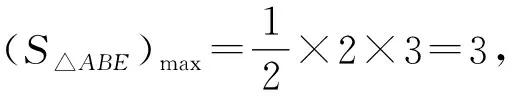
所以(SABCD)max=4(S△ABE)max=12.

评注已知两定点且动点到两定点的距离之比为定值,根据初中平面几何知识可以轻松地得出阿波罗尼斯圆与两定点所在直线以及两点的距离,快速找到阿波罗尼斯圆的圆心以及半径.通过圆上点在运动过程中到直线距离的变化可直接观察得到相关最值,求解快速准确.

探究策略5 平行四边形边长与对角线数量关系.

题目中只给出平面图形中边的关系和长度,基于菱形的面积可只用对角线之积解决,所以可只探究菱形对角线与边的数量关系.

因为4|AB|2=|AC|2+|BD|2,

所以|AC|2+9|BD|2=144.

当且仅当AC=3BD时,等号成立.

所以(SABCD)max=12.

评注平行四边形四条边的平方和等于对角线的平方和,巧妙地将本题中菱形的边长与对角线建立等量关系,进而建立对角线的相关数量关系(|AC|2+9|BD|2=144),最后用不等式相关知识求解最值.

探究策略6线段成比例+不等式.

鉴于菱形面积可利用对角线之积求解,故可利用题目条件将对角线用相关量表示,再考虑字母的轮换对称性,然后利用不等式相关知识求解最值.

连接BD,过点A,E分别作AD垂线,交点分别为G,F,易得|BG|∶|GF|∶|FD|=2∶1∶1.

又|BF|2+|EF|2=|BE|2,即x2+y2=9.

所以(SABCD)max=12.

评注依据本题中的对角线变化,又已知BE=3,故可以在△BEF中通过BE建立BF与EF的关系,再将菱形面积转化到BD与AG的积,利用重要不等式x2+y2≥2xy求解最值.

探究策略7线段成比例+三角运算.

通过平行、相似找到相关量之间的关系,再利用三角函数将双变量转化为单变量,将代数最值转化为三角最值.

评注通过平行线分线段成比例,三角形的相似将菱形的面积转化为三角形面积的倍数,在Rt△BEF中通过∠EBD建立关系将菱形的对角线转化为同一角度的不同三角函数值,再利用二倍角公式求解最值.

探究策略8 海伦公式.

菱形面积的求解本质上可分解为三角形面积求解.三角形面积如果只利用边长求解最直接的方法即海伦公式.

设AE=x,则AB=2x.

所以SABCD=4S△ABE

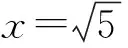
所以(SABCD)max=12.

数学是一个整体,不同的数学知识之间存在着紧密的、重要的联系.学生在获得数学理解的同时,应当能沟通知识之间的内在联系[2].但是,由于知识在教材中的呈现是相对独立的,教学又是以课时为单位设计学习内容,加上学生受到认知发展的限制,在没有引领的情况下,往往不容易发现知识之间的关联.因此在解题教学中,教师应利用适当的形式和方法从数学的逻辑上引导学生发现不同数学知识之间的内在联系,引导学生在解题的过程中不断地探索,进而展示数学知识的整体性与数学方法的一般性.