高中数学解题中圆的性质的应用

李雪梅

(安徽省利辛县第一中学,安徽 亳州 236707)

圆是一个最完美、最简洁的几何曲线,属于圆锥曲线的一种.圆具有旋转不变性,拥有无数条对称轴,且都经过圆心,所有半径的长度都一样,弦、切线、圆心角等也各具特色,有着自身的特殊性质.在高中数学解题训练中,部分试题虽然看起来同圆的关系不大,但是通过对题目信息的认真分析发现可以借助圆的丰富性质来解题,教师应指引学生根据具体题目准确、灵活地应用圆的性质,提高他们的解题能力.

1 应用圆的性质解决方程类问题

在高中数学解题教学中,与方程有关的习题难度比较大,处理此类试题时要综合用到多方面的知识,教师可引导学生应用圆的相关性质,使其形成清晰、准确的解题思路,帮助他们顺利求出题目结果[1].

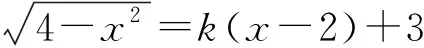
分析本题可以根据方程的特征构造出熟悉且简单的方程组,再逐层分解,转变成两个图形的交点问题,涉及到圆的性质,即先由数到形,再由形到数,将复杂问题变得简单化.

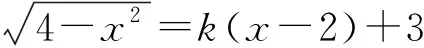
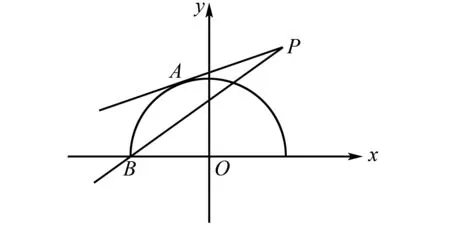
图1 例题1曲线图

2 运用圆的性质解决距离类问题

在处理高中数学求距离问题中,教师可以指导学生运用圆的性质辅助解决,通过圆的图象能清晰、直观地看到空间内两个点之间的距离,以此降低题目的难度,把复杂问题简单化,有效提高他们的解题速度[2].

例2 与点A(1,2)距离是1,与点B(3,1)距离是2的直线共有几条?

分析本题虽然能够使用代数法来解答,不过较为复杂,运用圆的性质可以将原题转变成确定两个圆的公共切线数量问题.

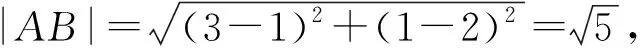
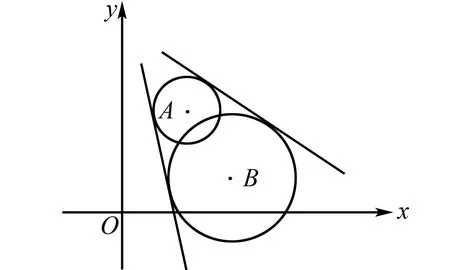
图2 例2解析图

3 采用圆的性质解决不等式问题

高中数学教师指导学生解答不等式问题时,除把握好不等式的性质以外,还要学会运用圆的相关性质进行分析,助推他们轻松突破障碍[3].

例3 已知实数x,y满足x2+y2-4x+6y+11=0,且不等式x-y+m<0,那么实数m的取值范围是什么?

分析处理这一问题时可以从几何视角展开分析,x2+y2+Dx+Ey+F=0所对应的图形就是圆,本题中的式子刚好符合这一特征,故能够运用圆的性质来解题.

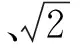
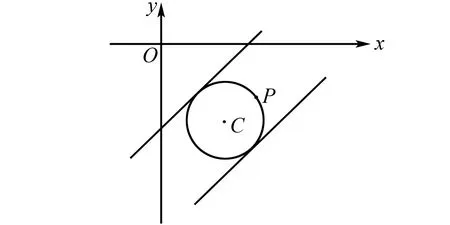
图3 例3解析图

4 使用圆的性质解决坐标类问题

在高中数学教学中,通常会有一些求坐标类的试题,这时教师可指引学生使用圆的性质进行解题,把圆的知识同坐标系的特征联系到一起,使其精准找到解题的突破口,快速确定解题思路,增强解题自信[4].

例4如图4所示,已知⊙O是以坐标原点为圆心、半径为1的圆,∠AOB=45°,点P(x,0)在x轴上运动,过点P且与OB平行的直线和⊙O有公共点,那么x的取值范围是什么?

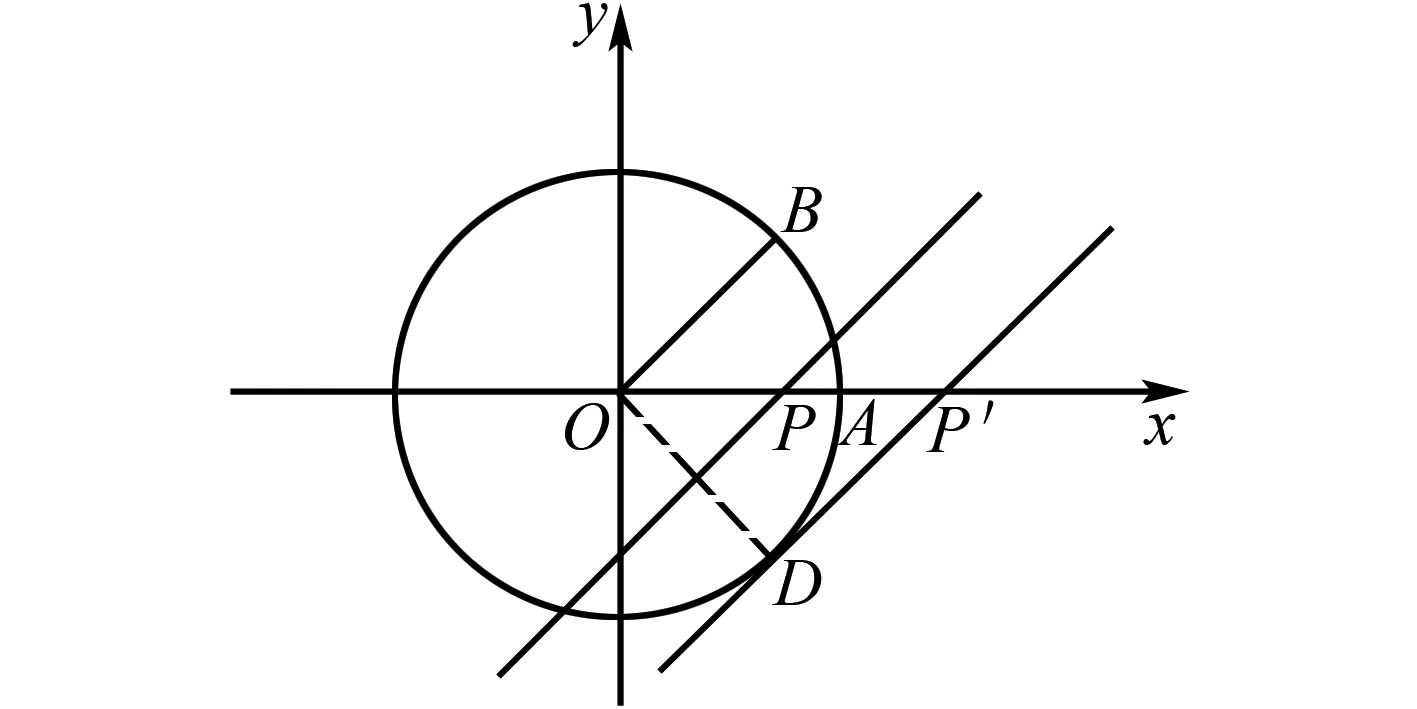
图4 例4解析图

分析虽然这是一道坐标类试题,但是涉及到圆的相关知识,所以要使用圆的相关性质来解题.

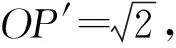
5 利用圆的性质解决最值类问题

高中数学教师在最值类解题训练中,可以引导学生利用圆的性质辅助求解,使其根据题目具体要求找到求最大值、最小值、最长或者最短的解决方法,帮助他们掌握高中数学中求最值问题的技巧[5].

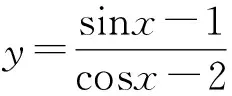
分析学生通过读题往往会感觉这一题目与圆没有关系,其实遇到这类问题时教师需提醒他们树立“见数思义”的思想意识,使其根据题干中的函数形式联系到直线的斜率,再结合圆的性质进行解题.

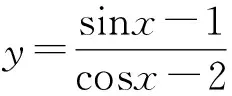
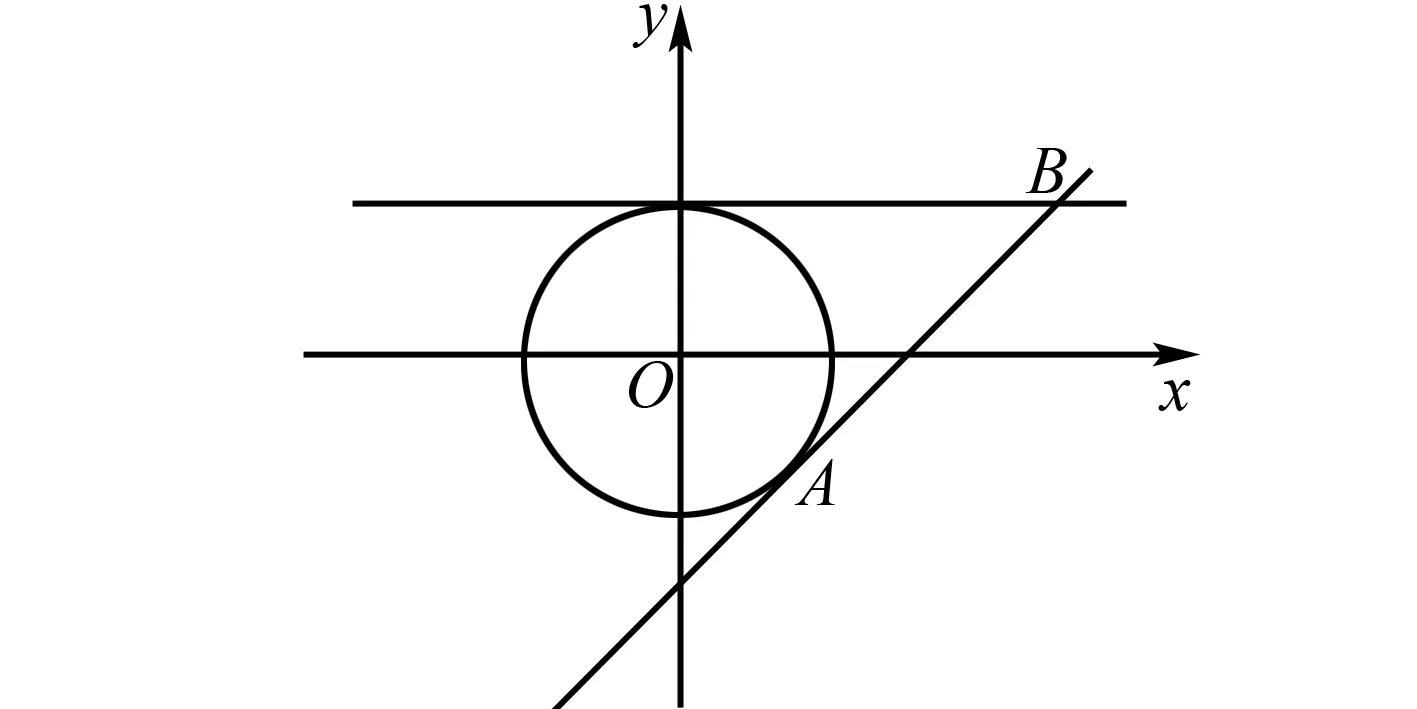
图5 例5解析图

6 借助圆的性质解决向量类问题

对于高中数学解题教学中的向量类试题而言,大部分学生都是初次接触,教师可以引领他们借助圆的性质进行解题,当然要以向量的计算法则为基础,使其能综合运用这些知识准确、轻松地求解[6].

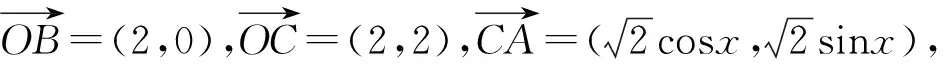
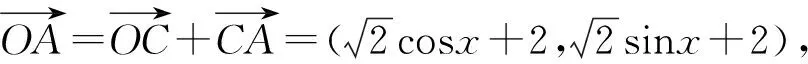
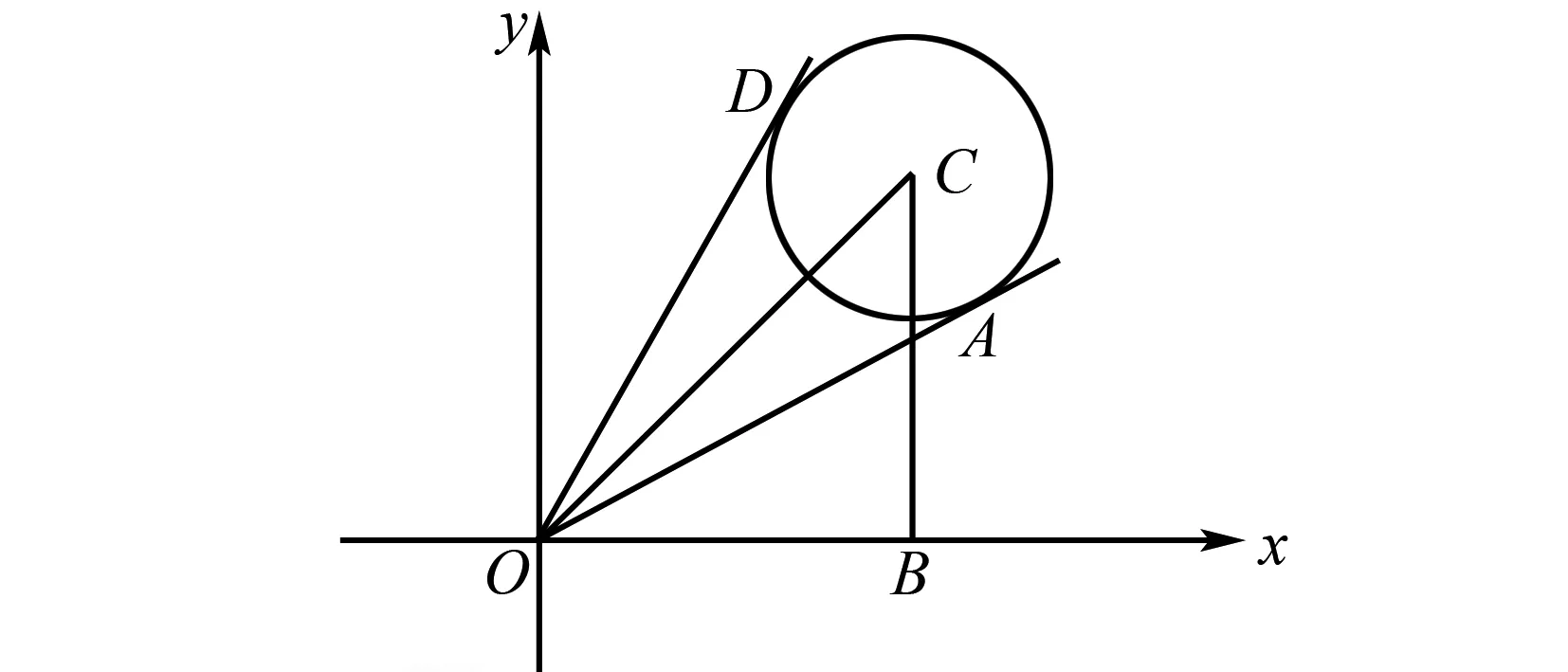
图6 例6解析图

综上所述,在高中数学解题活动中,圆的性质可谓是有着相当广阔的应用空间,不仅可以用来解决几何类问题,还有助于处理代数问题.教师应深刻意识到圆的性质的作用和优势,且将这一思想观念传递给学生,使其学会使用圆的性质解答方程、距离、不等式、坐标、最值与向量等问题,助推他们能够创新与优化解题思路,从而提高整体解题质量.