一道河南省大联考压轴题的解法探究

李昌成

(新疆乌鲁木齐市第八中学,新疆 乌鲁木齐 830002)

题目(2022年11月河南省大联考第16题) 已知实数x,y满足2x2-3y2-xy=1,则2x2+3y2的最小值为____.

解析因为2x2-3y2-xy=1,

所以(2x-3y)(x+y)=1.

令m=2x-3y,n=x+y,则

1 提出问题

这个题考查什么内容?有哪些通解通法?很多学生不明白.这个答案虽然没有问题,但是对于学生来说有点“突然”:为什么要因式分解?怎样分解出来的?初中已经把因式分解的十字相乘法删除,要是已知改为“2x2-xy-3y2=1”,将x视为主元,也许对分解因式的解题思路还有一些提示.况且分解后,怎么能预测从基本不等式找到出口呢?因此,本题上手还是有些困难的.

2 解法探究

策略1椭圆+三角代换+辅助角.

分析1 目标式2x2+3y2与椭圆方程左端很“形”似,令其为一个新变量就能实现三角换元,把问题转化为求三角函数的值域.

解法1 令2x2+3y2=t(t>0),

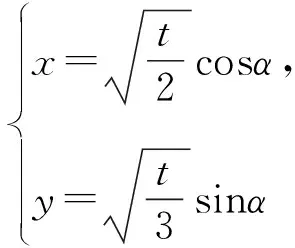
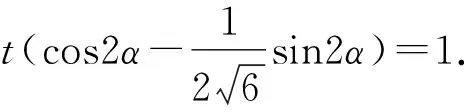
进一步由辅助角公式,得

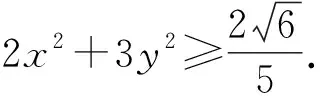
策略2 双曲线+三角代换+判别式.

分析2既然可以从目标式出发三角换元,同理可以从题设出发三角换元,只是曲线类型不同而已,运算大小不同罢了,这种思路也是很自然的[1].

解法2 由2x2-3y2-xy=1,得

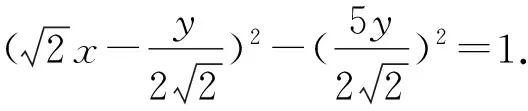
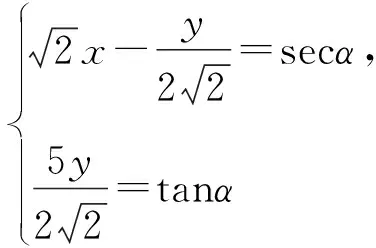
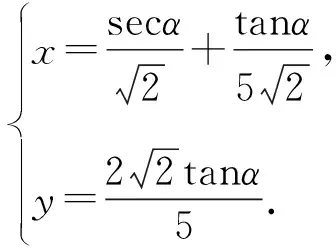
①

将①代入2x2+3y2,得

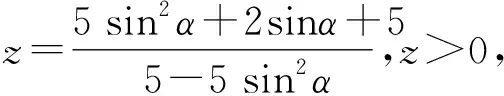
则(5+5z)sin2α+2sinα+5-5z=0.

②

由方程②有根,得

Δ=4-4(5+5z)(5-5z)≥0.

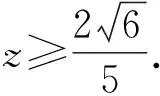
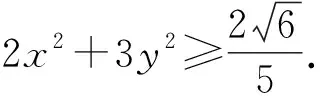
策略3 极坐标 +辅助角.

分析3 无论已知的左端还是目标式都是关于x,y的齐次式,因此可以考虑用极坐标来代换,将陌生的背景等价转化为我们熟知的模型.

解法3 由极坐标公式x=ρcosθ,y=ρsinθ,结合已知2x2-3y2-xy=1,得

2(ρcosθ)2-3(ρsinθ)2-ρcosθ·ρsinθ=1.

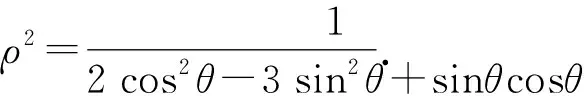
那么2x2+3y2=2(ρcosθ)2+3(ρsinθ)2

=ρ2(2cos2θ+3sin2θ)

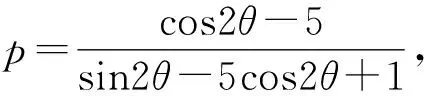
那么psin2θ-(5p+1)cos2θ=-p-5.

由辅助角公式,得

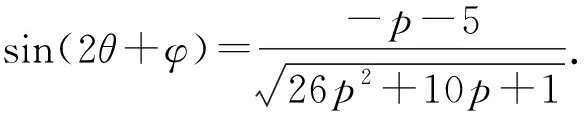
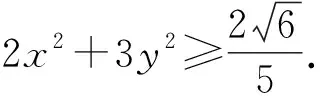
策略4 “韦达技巧”+复合函数.

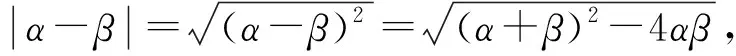
解法4 由2x2-3y2-xy=1,得

2x2-3y2=xy+1.

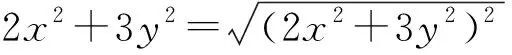
令xy=n,m=25n2+2n+1,

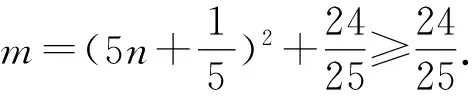
策略5 整体代换+主元思想.

分析5 将目标式看成分母为1的分式,并视“1”为已知中的右端,进行整体换元,构造关于x(或y)的一元二次方程,利用判别式求解.

又因为2x2-3y2-xy=1,

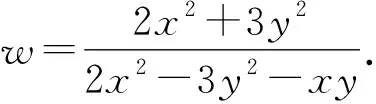
整理,得2wx2-3wy2-wxy=2x2+3y2.

视x为主元,进一步整理,得

(2w-2)x2-wyx-3wy2-3y2=0.

③

由方程③有根,得

Δ=(wy)2+4(2w+2)(3wy2+3y2)≥0.

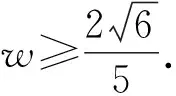
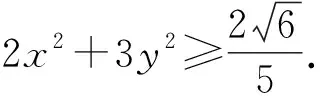
策略6 齐次化+判别式.

分析6 结合解法5,可以将目标式转化为二元齐次双变量分式函数,通过换元得到一元函数.

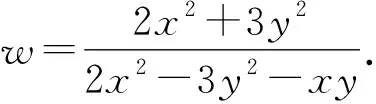
不失一般性,当x≠0时,

于是(3w+3)u2+wu+2-2w=0.

进一步得Δ=w2+4(3w+3)(2w-2)≥0,

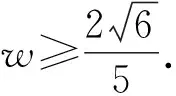
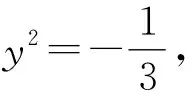
策略7齐次化+对勾函数.

分析7 由解法6得到的一元函数,还可以整体处理后向对勾函数转化,通过对勾函数求最值.

解法7 由解法6,得

不失一般性,当u≠4时,

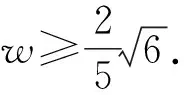
当u>4时,w<0,不合题意,舍去.

当u=4时,w<0,不合题意,舍去.

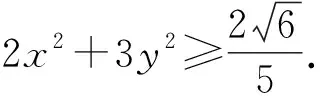
当前正在深入推进新课程新高考改革,数学高考卷全力推进对数学核心素养的考查,对学生的创新能力要求较高,这是国家选拔高水平人才的需求.那么我们在教学中就要积极适应这种新格局,对于这种新题型,或称拔高性试题,我们务必从思路、通解通法上下功夫,教会学生利用已有的知识,主动有效地与已知联系起来,进而选择恰当的方法,突破新背景下的新试题,以此展示自己较高的数学素养,而不是束手就擒,惊慌失措.另外,一题多解能打开学生的思路,培养创新品质,在日常教学中,我们要大胆放手,给学生机会,给其充足的思考时间,不可继续使用满堂灌的填鸭式教学方法,新高考模式必须有新的教学方式与之相匹配,否则,我们无法跟上高考改革的步伐.