高中数学不等式解题技巧思考

沈子儒

(安徽省利辛县第一中学,安徽 亳州 236700)

不等式是用符号大于、小于、大于等于、小于等于等表示大小关系的一类式子.在高中数学中,涉及题型比较广泛,包括选择题、填空题与计算题等,假如学生没有透彻理解不等式知识,难以熟练掌握解题技巧,他们就无法很好地解题.高中数学教师应高度重视不等式解题技巧的思考,利用各种常见的题型组织学生进行集中训练,使其结合具体题目使用相应的技巧分析和解答,不断提高他们的解题水平,反过来辅助对理论知识的深化理解.

1 不等式的反证解题技巧

不等式作为高中数学教学中比较重要的一部分内容,通常以各种题型出现在平常练习与考试当中.解答有关不等式的题目时往往要用到各种技巧,其中反证方式应用的较为广泛,这是以正难则反为基础形成的,在证明类的问题中使用有着不错的效果.对此,高中数学教师可指导学生在处理不等式证明类题目时采用反证法,使其将整个证明过程变得更为便捷与简单,将不等式证明问题的解答变得更为高效,帮助他们掌握不等式证明题的解题技巧[1].

例1已知a+b+c>0,ab+bc+ac>0,abc>0,请结合以上条件证明a>0,b>0,c>0.

解析根据题干中提供的条件abc>0,能够得出a,b,c均不可能是0,这里要用到反证的方式.

假设a<0,则bc<0,又因为a+b+c>0,所以b+c>-a,由此可以得到a(b+c)<0.

所以a(b+c)+bc<0.

不过这一式子明显同题干中提供的信息相冲突,所以说这个假设是无法成立的,也就是表明a>0,b>0,c>0.

2 不等式的换元解题技巧

处理部分数学问题时,把其中一个式子当作一个整体来看待,且运用一个变量进行替换,从而将问题变得更为简单,这就是常用的换元法,广泛适用于方程、函数、不等式等解题实践中,根本思想是转化,关键在于构建“元”与设置“元”.在高中数学不等式解题训练中,教师可以引导学生采用换元解题技巧,把研究对象进行变换,问题转移至新对象上面,目的是让非标准的问题变得标准化,复杂问题变得简单化,最终让他们轻松解答不等式问题[2].

例2 已知a,b,c∈R+,请证明abc≥(b+c-a)(c+a-b)(a+b-c).

解析使用换元法假设x=b+c-a,y=c+a-b,z=a+b-c,这时可以转变为证明

(x+y)(y+z)(x+z)≥8xyz.

由于x=b+c-a,y=c+a-b,z=a+b-c,

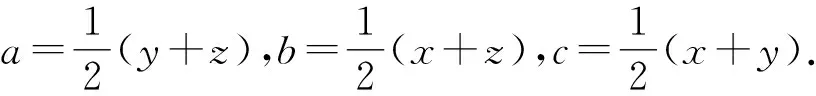
因为a,b,c∈R+,所以当xyz<0时,可以得到(x+y)(y+z)(x+z)≥8xyz.

当xyz>0时,有x,y,z∈R+,假如x,y,z三者当中有任意两个比0小,那么c≤0与c>0是相矛盾的,由此得到

则(x+y)(y+z)(x+z)≥8xyz.

首先检测500条时态RDF数据的不一致性，首次计算节点的生命区间。左边就是存在不一致性数据，右边是修改后的一致性数据。

然后把x,y,z代入到原式中可以得到

abc≥(b+c-a)(c+a-b)(a+b-c).

3 用不等式性质解题技巧

在高中数学不等式解题教学中,教师应关注学生对不等式基本性质的合理运用,这是一项最基础的解题方式与技巧,可以应用至各种类型的不等式试题中,不少题目都要用到不等式的基本性质.如:不等式具有传递性,也就是如果a>b,b>c,则a>c;不等式还有可加性特点,假如a>b,就表明a+c>b+c,c>0时,ac>bc.所以,学生可以利用不等式的基本性质进行解题,能够快速找到解题的切入口,继而提高他们解题的准确率[3].

例3 平面上有n个圆,其中每两个圆都相交于两点,每三个圆都不相交于同一个点,请证明n个圆将平面分成f(n)=n2-n+2个部分.

解析(1)归纳法,当n=1时,一个圆可以把平面分成两个部分,即f(1)=12-1+2=2,故命题成立.

(2)假设n=k,该命题成立,也就是说k个圆将平面分成f(k)=k2-k+2个部分,则设第k+1个圆的圆心为O,根据题意可知它与k个圆中每个圆相交于两个点,又无三个圆相交于同一点,那么与其它k个圆相交于2k个点,以此结合题目中提供的条件有效证明出命题的结论,这是对不等式基本性质的充分运用.

4 线性规划题的解题技巧

例4已知a>0,参数x,y会满足以下三个条件,x+y≤3,x≥1,y≥a(x-3),如果z=2x+y的最小值为1,那么a的值是什么?

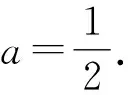
图1 坐标轴示意图

5 用数形结合解不等式题

数形结合指的是“数”与“形”之间的有机结合,这是数学思想方法中最为常用的一种,不仅可以用来解答不等式相关的试题,还能够运用至其它数学试题的解答中,与其它解题技巧相比,数形结合能够将题目变得更为形象与直观,有助于学生快速找到解题思路,让他们高效解题.当运用数形结合思想解决不等式类题目时,高中生要注重“以形助数”的应用,将“数”由“形”的形式呈现出来,使其找到更简便的解题方法,锻炼他们的解题技巧[6].

例5 已知关于x的不等式x2≤4-|2x+m|,如果至少存在一个x≥0使得该不等式成立,那么m的取值范围是什么?

解析对原不等式进行整理后得到|2x+m|≤-x2+4,将不等式的左右两边均看作成函数,即为y=|2x+m|与y=-x2+4,这里要从反面思考问题,即:如果对于任意的x≥0,均有|2x+m|>-x2+4,在同一个平面直角坐标系中画出两个函数图象,如图2所示,根据图片信息能发现当m的值发生变化时,函数y=|2x+m|的图象将会沿着x轴进行运动,图2中两个临界条件,分别对应于m>4,或者m<-5,由此表明要想满足题意m的取值范围应该是[-5,4].

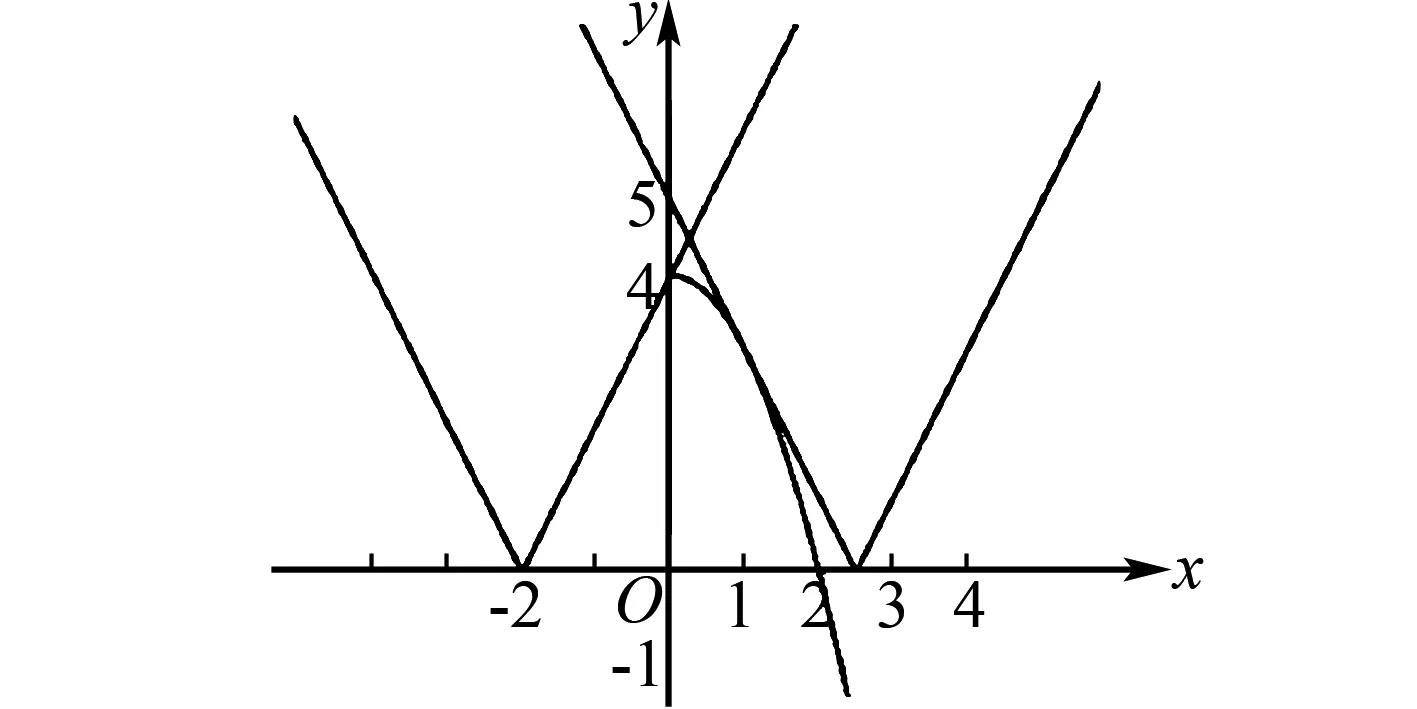
图2 函数图象示意图

6 不等式高次题解题技巧

在高中数学不等式相关内容教学中,高次不等式问题不仅属于一项重要教学内容,还是一大难点,处理此类不等式问题时,最经常出现错误的地方就是划分区域时容易混乱,无法准确判断出特殊的区域或者特殊点.对此,高中数学教师可以结合高次不等式开展专题训练,指引学生采用因式分解的方法进行解题,借此把高次不等式转变为低次不等式,复杂问题作简化处理,将问题变得更为清晰明了,使其极易找到解题的切入点,继而掌握解题技巧[7].

例6 求解不等式(x-1)(x-2)(x-3)>0.

解析结合题目中给出的三次不等式方式能够画出如图3所示的图象,第一步,画出一个坐标轴,在坐标轴上面标出1,2,3三个点的位置,由此将坐标轴划分为4个区间;第二步,把靠近右边区间看作为正,其它的看作为正负相间,在各个区间内标出正负号;第三步,用“+”表示不等式大于0,用“-”表示不等式小于0,这样能更为形象地观察到不等式的区域,可明显得出x的取值范围是13.

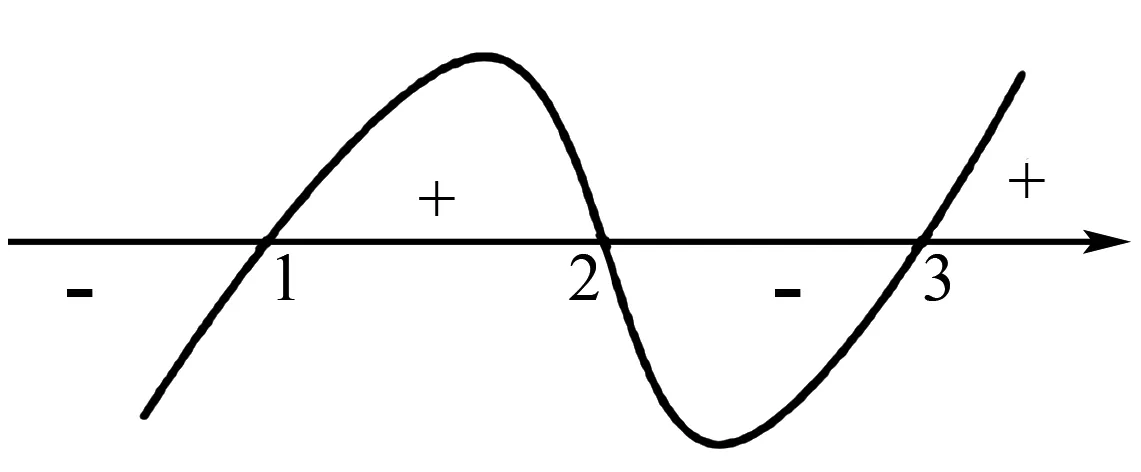
图3 不等式曲线图

使用“穿根法”进行解题时,应先画出一个坐标轴,再在坐标轴上面绘制出不等式的情况,结合所画坐标轴及穿线顺序判断不等式的大小情况,这一解题技巧显得简单、直观,解题难度有所降低.

总而言之,在高中数学教学活动中,解题训练是相当关键的构成部分,是学生运用所学知识处理问题的主要途径与渠道,尤其是在不等式教学实践中,教师要充分考虑到不等式知识的广泛运用,精心设计多种多样的题型展开不等式解题训练,使其通过亲身实践掌握大量的不等式解题技巧,逐渐树立起学习数学的自信心,全面提升他们的数学解题水平.