巧用构造法 妙证不等式

陈国龙

(扬州大学数学科学学院,江苏 扬州 225002)

不等式在高中数学学习中占据了重要地位.在函数、几何等知识中应用广泛,在高考和数学竞赛试卷中,不等式的证明一直都是考查的重点与难点.构造法是指当按固有思维难以快速有效解决问题时,尝试结合已知条件、性质等,选择一定的数学对象去构造新的数学载体,从而解决问题的分析方法[1].它是不等式证明中的一种重要方法,而本文正是从构造不同数学载体的角度,用实例来分析总结高中数学竞赛试题中证明不等式的几种方法.

1 构造恒等式

由于恒等式的结果是显然的,所以我们在证明不等式的时候,常常会通过补充不等式中省去的某些项,进而挖掘不等式背后的恒等式,从而找到证明的突破口.

例1已知a2+b2+c2+d2=1, 求证:(a+b)4+(a+c)4+(a+d)4+(b+c)4+(b+d)4+(c+d)4≤6.

①

分析首先通过观察,发现已知代数式与所证不等式的次数不一致,为了保持一致,很显然我们可以得到(a2+b2+c2+d2)2=1,其次我们肯定要设法找出所得条件与①式之间的关系.注意到要使(a+b)4中a的奇次项不在(a2+b2+c2+d2)2的展开项中出现,可以配上(a-b)4与之相消,这样就找到了关键突破口.

证明考虑和式:(a-b)4+(a-c)4+(a-d)4+(b-c)4+(b-d)4+(c-d)4,不难发现它与①式左端恰好构成恒等式,即

(a+b)4+(a-b)4+(a+c)4+(a-c)4+(a+d)4+(a-d)4+(b+c)4+(b-c)4+(b+d)4+(b-d)4+(c+d)4+(c-d)4=6(a2+b2+c2+d2)=6.

则显然①式得证.

2 构造函数

根据题中所给的代数式的关系以及特征,构造适当的函数,利用函数的图象与性质,例如函数单调性,可以有助于不等式的证明.

例2设xk≥1,k=1,2,…,n,且(1+x1)(1+x2)…(1+xn)>2λ,求证:x1+x2+…+xn>λ.

分析首先通过观察,确定构造的函数类型:以2为底的对数函数;其次,根据已知条件确定构造的具体函数:函数f(x)=x-log2(1+x);分析其单调性,即可完成证明.

证明由条件不等式(1+x1)(1+x2)…(1+xn)>2λ,不等式两边可同时取以2为底的对数,即log2(1+x1)+log2(1+x2)+…+log2(1+xn)>λ.

又因为f(x)>f(1)=0,则x>log2(1+x)在x∈[1,+∞)时恒成立.

故x1+x2+…+xn>log2(1+x1)+log2(1+x2)+…+log2(1+xn)>λ.

3 构造几何图形

如果题目中所给的不等式有明显的几何意义,或者通过观察能够以某种方式与几何图形建立相应的联系,那么通过构造图形,实现“数形结合”,使题设的条件及关系在图形中得以体现,从而利用构造的几何图形证明不等式.

图1 点与点距离之差示意图

4 构造对偶式

将函数式F中所有的“·”变成“+”,“+”变成“·”,“0”变成“1”,“1”变成“0”,并保持原函数中的运算顺序不变,则得到的新表达式称为函数式F的对偶式[2].解题时,在一些轮换不等式中,依据已知式子的结构特征,构造结构一致,具有某种对称关系的一对对偶式,就能通过一系列基本运算,巧妙地证明不等式.

例4若a1+a2+…+an=1,求证:

分析观察该不等式为轮换不等式,根据其结构特征,构造相应的对偶式,然后利用加减乘除四则运算化简问题,从而证明不等式.

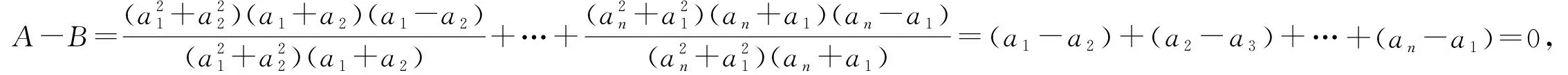
所以A=B.

又因为根据算术几何平均不等式,有

5 构造数列

若题目是有关n的不等式时,可以考虑构造辅助数列,并类比构造函数,利用数列的性质,如单调性来证明不等式.

例5 设a1,a2,…,an(n≥2)都大于-1且同号,求证:(1+a1)(1+a2)…(1+an)>1+a1+a2+…+an.

分析观察题面可知,我们可以考虑构造新的数列来进行辅助证明,再根据我们所要证明的不等式,确定构造的数列,即将不等式左右两端相减组成一个新数列,最后利用新数列的单调性证明不等式.

证明构造数列xn=(1+a1)(1+a2)…(1+an)-(1+a1+a2+…+an)(n≥2),则

xn+1-xn=an+1[(1+a1)…(1+an)-1].

若ai>0(i=1,2,…,n+1),由上式可得

xn+1>xn.

若-1xn.

因此数列{xn}是一个单调递增数列(n≥2).

由于x2=(1+a1)(1+a2)-1-a1-a2=a1a2>0,则对一切n≥2,xn>0,从而原不等式成立.

6 构造反例

在不等式的证明中,有时也会出现证明存在有限种情况使得不等式成立,或者是否对于任意满足条件的数,不等式恒成立的问题.在数学学习中,反例可以用来说明一个命题是假命题,它满足该命题的条件,但是不满足该命题的结论[3],可以很好地解决这类不等式的证明问题.

例6设n为一个大于2的奇数,求证:当且仅当n=3或5时,对任意a1,a2,…,an∈R,有下面不等式成立:

(a1-a2)(a1-a3)…(a1-an)+(a2-a1)(a2-a3)…(a2-an)+…+(an-a1)(an-a2)…(an-an-1)≥0.

分析只需证明当n=3或5时,不等式成立,再利用反例证明当n≥7时,不等式不成立即可.

证明不妨设a1≤a2≤…≤an.

A5=(a1-a2)(a1-a3)(a1-a4)(a1-a5)

+(a2-a1)(a2-a3)(a2-a4)(a2-a5)

+(a3-a1)(a3-a2)(a3-a4)(a3-a5)

+(a4-a1)(a4-a2)(a4-a3)(a4-a5)

+(a5-a1)(a5-a2)(a5-a3)(a5-a4).

由于(a3-a1)(a3-a2)(a3-a4)(a3-a5)≥0,而A5前2项之和为(a2-a1)[(a3-a1)(a4-a1)·(a5-a1)-(a3-a2)(a4-a2)(a5-a2)]≥0,同理可得A5后2项之和也不小于0,故A5≥0.

当n≥7时,构造反例如下:

令a1=a2=a3