一道导数模考压轴题的探究
2023-08-30林国红
林国红
(广东省佛山市乐从中学,广东 佛山 528315)
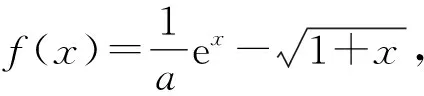


由于问题(1)较为简单,本文不作讨论,下面从不同视角,对问题(2)进行解答与探究.
1 解法探究
视角1 放缩法.

由ex≥1+x(x=0时取等号),得
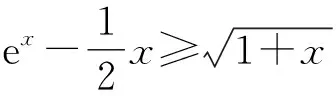
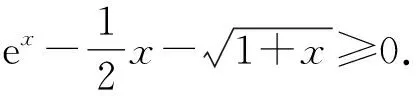





故g(x)在[-1,+∞)上单调递增.

所以g(x)≥g(-1)≥0.













视角2 主元法.
证法3①当a=1时,由证法1,可得

将a看作主元,令
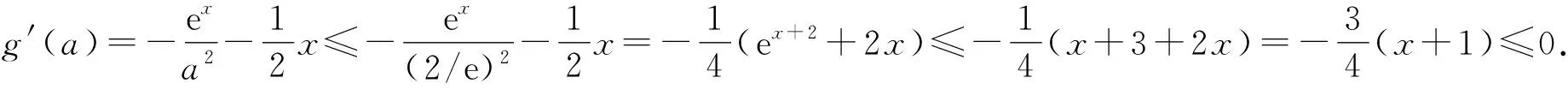






证法4①当a=1时,由证法1,可得

将a看作主元,令
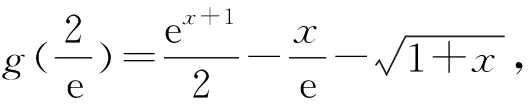

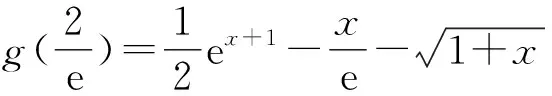






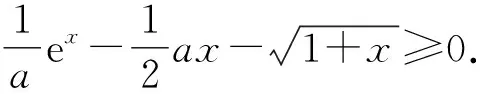
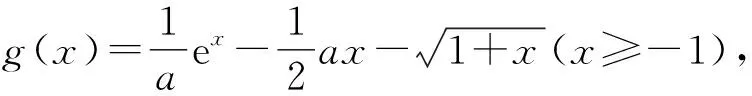


将a看作主元,令






评注在处理不等式有关问题时,若题目中有多个变量,且以x为主元解答较困难时,可以尝试改变分析问题的角度,重新确立主元,排除参数的干扰.这样往往会有“山穷水尽疑无路,柳暗花明又一村”的豁然开朗之感,从而可化繁为简,化难为易[2].
视角3 配方法.
证法6当0
由ex≥1+x,可得
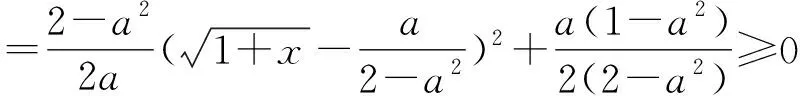
当且仅当x=0,a=1时,等号成立.

证法7当0
由ex≥1+x,可得

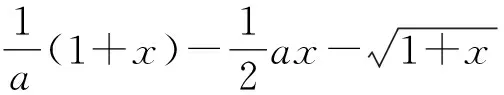


评注证法6与证法7先利用常见函数不等式ex≥x+1进行放缩,并结合二次函数的配方法来证明,证法巧妙,简便,极大简化了证明过程.两个证法本质上是一样的,但证法7换元后更容易看出是二次函数的形式.
视角4 换元法.
证法8当0 当t>a时,g′(t)>0,故g(t)在(a,+∞)上单调递增. 于是g(t)≥g(a)=-alna≥0. 评注本证法利用常见函数不等式ex≥x+1进行放缩,消去式子中的根式,然后换元构造新函数,通过求新函数的最值来证明,证法的运算量较少,过程也较为简洁. 试题分步设问,逐步推进,由浅入深,重点突出,较好地达到了考查目的,其思维过程较好地体现了函数与导数的核心内容和基本思想方法的考查. 数学的魅力在于“变化”,有“变”才能“活”,恰当的“变式”能避免学生在低层次重复,能使学生多角度、全方位地理解知识,思维能力得到拓宽和加强.所以数学教学不仅要解决问题,还要注重问题的变式拓展,引导学生积极探索一题多变、一题多用,达到举一反三、触类旁通的目的. 由原题及其证法,可得题目的变式: 含参的函数不等式的证明问题,特别是以ex或lnx为背景的函数不等式证明,是高考中的重要考点,倍受命题者青睐,常作为压轴题频频亮相.例如: 例1 (2018年高考全国Ⅰ卷文科第21题)已知函数f(x)=aex-lnx-1. (1)设x=2是f(x)的极值点,求a,并求f(x)的单调区间; (1)求曲线y=f(x)在(0,-1)处的切线方程; (2)证明:当a≥1时,f(x)+e≥0. 学数学离不开解题,遇到一道经典试题,要从多角度、深层次探寻其解法,通法也好,巧法也罢,不单要比较其优劣,还要清楚其中的方法内涵,知晓其中的来龙去脉,方能实现试题研究价值的最大化.另外,不要只满足于问题的解决,要通过变式、类比进行研究,寻求问题的增长点,从而达到做一题会一类,甚至会一片的目的,积累良好的数学思维和实践经验,最终在解题思路上产生质的变化,使思维得到发展.









2 试题的思考与变式


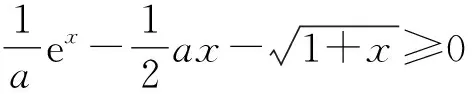
3 链接高考

