某低后坐自动炮动力学特性与优化研究
2023-08-29韩如锋袁永强唐蓬博刘野王永存
韩如锋,袁永强,唐蓬博,刘野,王永存
(西北机电工程研究所,陕西 咸阳 712099)
某低后坐自动炮,发射底部可排气式新型埋头弹药,采用惯性炮闩精确控制膛内开闩泄压时机,实现膨胀波原理发射。埋头弹的弹丸镶嵌在圆柱形药筒内,大幅缩短了整体长度,使得炮塔结构能够更加紧凑,有效提高了现役战车的综合性能[1]。但同时,埋头弹火炮存在高膛压下身管烧蚀、闭气与抽壳困难等情况。膨胀波火炮通过精确控制炮闩在内弹道时期的打开时间,使膨胀波在炮口处才追上弹丸的尾部,实现了在不影响火炮初速和杀伤威力的前提下大幅度减小火炮后坐力与后坐冲量的效果[2-3]。但由于存在火药燃气的后喷,在结构上不便于采用传统的后方装填方式。
埋头弹火炮与膨胀波火炮存在天然结合的特点:一是埋头弹火炮具有的摆膛式装填方式是实现膨胀波火炮工程化应用理想选择;二是膨胀波火炮开闩泄压降低了平均膛压,有利于解决埋头弹火炮身管寿命、密封与抽壳等难题;三是在保证威力基本不变的前提下,大幅减小了后坐力,满足未来轻型装甲车辆的适配性要求。
某低后坐自动炮将膨胀波发射机理与埋头弹火炮融合应用,实现了系统的集成创新,其结合了埋头弹火炮与膨胀波火炮各自的性能,同时又有别于二者,其发射规律的影响因素也各不相同。笔者通过建立发射过程的内弹道集总参数模型和动力学模型,分析其动力学特性,对该型火炮的总体参数优化与匹配具有一定的指导意义。
1 内弹道集总参数模型
根据某低后坐自动炮的工作原理,考虑膨胀波发射机理与埋头弹火炮融合的工作机制,结合经典内弹道模型,计及惯性炮闩的运动过程,建立了某低后坐自动炮的内弹道集总参数模型[4-5]:
(1)
(2)
(3)
(4)
式中:Z为火药相对已燃厚度;k为绝热指数(θ=k-1);n为火药燃速指数;S为炮膛截面积;f为火药力;ω为装药量;Δ为装填密度;φ为次要功计算系数;m为弹丸质量;ψ为已燃相对体积;l、v分别为弹丸的行程和速度;l1、v1分别为惯性炮闩的行程和速度;pE为惯性炮闩启动压力;lE为惯性炮闩开闩前行程;FS为炮闩缓冲器的力;m1为惯性炮闩质量;S1为惯性炮闩喷口截面积;η、τ分别为相对流量、相对温度;ρp为火药密度;α为气体余容。
通过数值求解,获取了闭膛发射与膨胀波发射两种发射模式下对应的p-t数值解,并结合身管压力传感器进行了试验验证,仿真结果与试验结果的对比曲线如图1所示。结果表明,两种发射模式下各自对应的p-t仿真值与试验值均较为吻合。

通过数值求解,获取了闭膛发射与膨胀波发射两种发射模式下对应的v-t数值解,仿真结果曲线如图2所示,可以看出,两种发射模式下的炮口初速基本不变。

在此基础上,对闭膛发射与膨胀波发射对应的炮膛合力与炮膛合力的冲量进行了仿真,炮膛合力对比曲线如图3所示,仿真结果表明,膨胀波发射方式相比闭膛发射方式,使得炮膛合力冲量有效减小了31.5%。

2 虚拟样机模型
2.1 运动模型
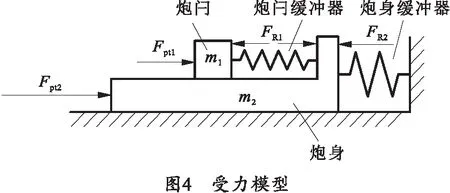
将整个运动模型简化为两自由度的弹簧-阻尼质量系统,整个系统受力模型如图4所示,系统为两自由度模型[6]。图中,Fpt1为火药气体在闩体上的作用力;Fpt2为火药气体作用在炮身的炮膛合力;FR1为炮闩缓冲器力;FR2为全炮后坐阻力;m1为闩体质量;m2为后坐部分质量。
2.2 模型简化与假设
根据某低后坐自动炮的结构特点,在不影响系统运动规律的前提下,作出以下简化与假设[7-8]:
1)除缓冲簧以外的结构件均视为刚体;
2)自动炮的摇架设置为与大地固定,且不考虑其受力响应;
3)把各个部分运动关系相互一致的部件逐个进行合并;
4)将火药燃气的作用力视为集中力,以集中力的形式施加;
5)摩擦力仅考虑在主要接触环节施加。
2.3 拓扑结构
自动炮后坐运动部分以滑动副方式在摇架上后坐-复进;惯性炮闩与自动炮以碟簧相连接,以滑动副方式在自动炮滑轨上移动;全炮缓冲器与摇架及自动炮以缓冲簧-阻尼形式相连。在缓冲器内部,外筒、缸体、螺盖与摇架固连;芯轴、轴套、导杆以滑动副形式在缓冲器内滑动;轴套与导杆之间以弹簧-阻尼相连;轴套与导杆在运动过程中皆与外筒存在面接触;在运动过程中芯轴与导杆、芯轴与轴套之间均存在实体接触。拓扑结构如图5所示。其中Hf、Hc、Ht、Ho分别代表固定副、接触副、移动副和其他连接关系。

2.4 载荷分析
喷口打开之前,炮闩和炮身受到的火药气体作用力分别为
(5)
(6)
式中:φ为次要功系数;ω为装药量;m为弹丸质量;A为炮膛横截面积;Svent为喷口活塞面积;p为膛内平均压力。
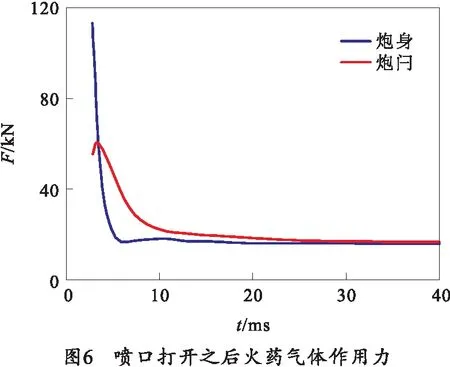
喷口打开之后,火药气体作用力使用FLUENT进行数值模拟计算,闩体和身管的受力大小如图6所示,为方向向前的阻力。
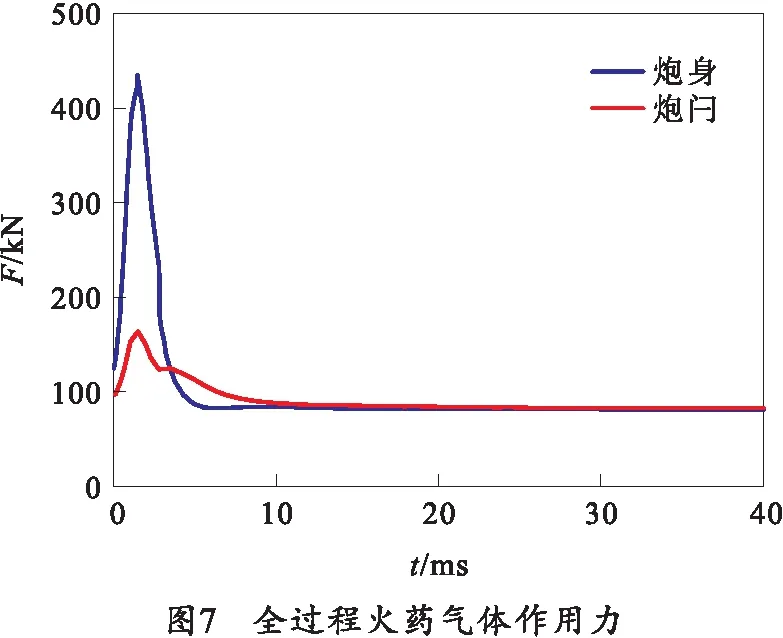
整个过程的火药气体对炮身和炮闩的作用力如图7所示。通过矢量力的形式分别施加在炮身和炮闩上。
炮闩缓冲力FR1为
(7)
式中:t为单片碟簧厚度;D为碟形弹簧外径;x为弹簧总压缩量;h0为缓冲器压平时单片碟形弹簧变形量的计算值;n为对合碟簧的个数;E为弹簧材料的弹性模量;μ为弹簧材料的泊松比;K1和K4为计算系数。
炮闩缓冲力的表达形式采用RecurDyn中单向力方式,力值为关于弹簧压缩量即炮闩相对全炮的后坐位移的单变量表达式函数。
全炮后坐阻力为
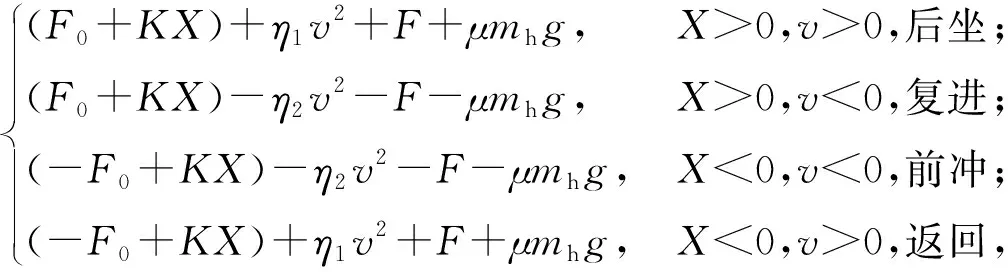
(8)
式中:F0为弹簧预压力;K为弹簧刚度系数;X为后坐位移;η1、η2为液压阻尼结构参数,其值与液压阻尼器的结构和液压油的性质有关;v为后坐速度;F为密封装置摩擦力;μ为后坐部分与架体之间的摩擦系数;mh为后坐部分质量;g为重力加速度。
液压阻力的表达形式采用RecurDyn函数库中状态条件判断IF函数[7]:
IF(VX(1)∶η1*VX(1)*VX(1),0,-η2*VX(1)*VX(1)).
建立好的虚拟样机模型如图8所示。
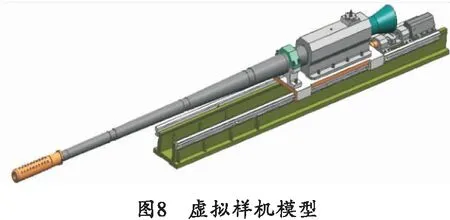
3 试验验证
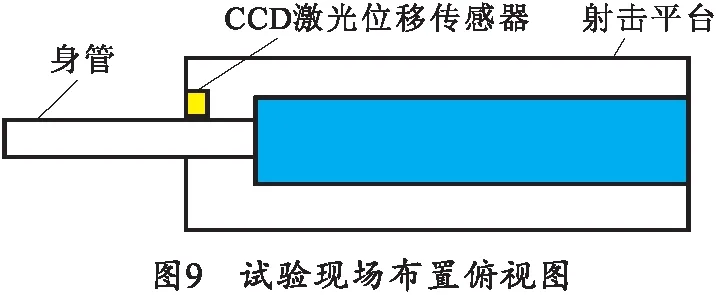
采用激光CCD传感器对后坐位移进行测试,现场布置原理如图9所示。其中CCD激光位移传感器固定在地面台架上,其发射的激光垂直正对火炮后坐部分的端面。射击试验场景如图10所示。

将闭膛发射与膨胀波发射两种发射模式下的后坐部分位移-时间仿真值与测试值进行对比,如图11所示,二者吻合度较高,验证了动力学模型的正确性。

某低后坐自动炮缓冲器的特性使得最大后坐力值出现在最大后坐位移处,依据工程算法,FR1=2(KX+F0),带入闭膛发射与膨胀波发射时的最大后坐位移测试数据,对应得到最大后坐力FR1,如表1所示,膨胀波发射模式使得最大后坐力减小高达74%。

表1 闭膛发射与膨胀波发射最大后坐力试验值对比
4 炮闩缓冲力优化模型
炮闩缓冲器采用碟簧缓冲,具有很广范围的变刚度非线性特性。可通过适当选择碟形弹簧压平时变形量h0和厚度t之比,得到不同特性曲线,也可采用复合不同厚度、不同片数等的组合方式使弹簧特性在很大范围内变化。
将开闩前定义为第1阶段,开闩后定义为第2阶段。第1阶段,惯性炮闩在最佳开闩时间点打开,因此,第1阶段的惯性炮闩缓冲簧支撑刚度在优化前后应保持基本不变,以保证相同的最佳开闩时机;第2阶段,惯性炮闩打开,由于结构特征决定了该自动炮后喷气体流场与炮闩所处的位置无关,所以可将第2阶段惯性炮闩缓冲簧支撑刚度减小,利用较长后坐行程和时间减小开闩阻力。通过惯性炮闩缓冲簧支撑刚度的匹配优化,达到减小最大开闩阻力的效果,为惯性炮闩轻量化提供参考依据。
综上,建立优化模型:
(9)
式中:n为片数;D为碟簧外径;λ为炮闩相对炮尾最大后坐行程。
借助多岛遗传算法[8],基于多学科优化平台Isight软件,调用RecurDyn动力学仿真软件计算,优化计算流程如图12所示[9-10]。

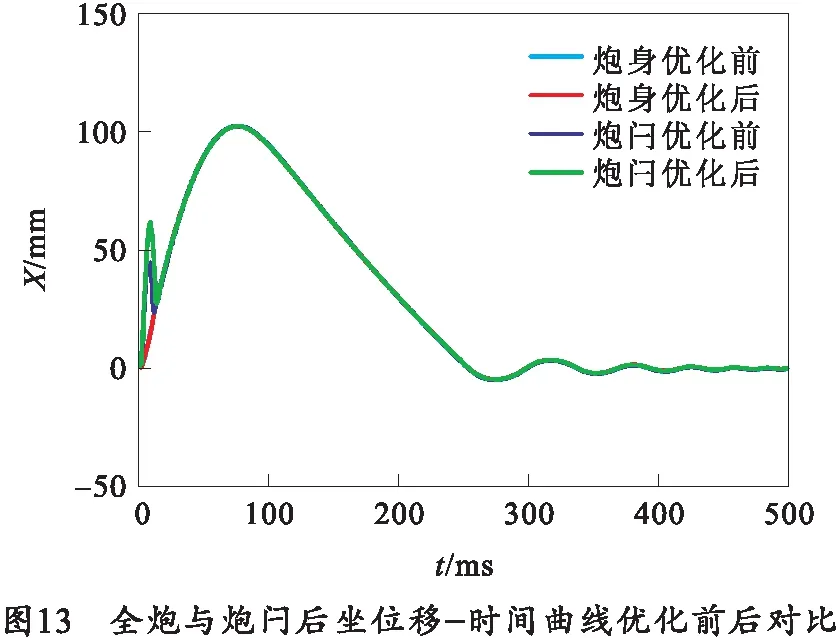
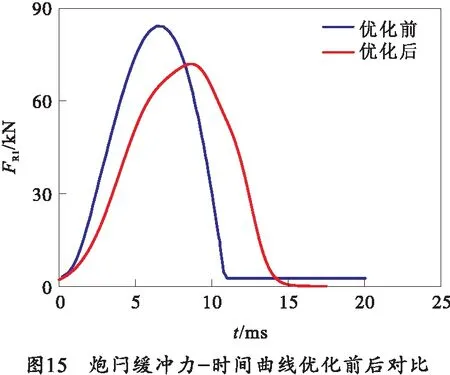
优化算法求取了炮闩缓冲装置的最优参数,如表2所示。优化前后,炮身与闩体后坐位移-时间以及炮身、炮闩受力-时间仿真曲线对比如图13~15所示。结果表明在结构安装尺寸保持不变的前提下,全炮后坐位移和阻力基本不变,炮闩最大阻力减小约14.2%。

表2 优化前后设计变量和目标函数值

5 结束语
1)通过仿真计算与试验测试数据的对比分析,验证了所建立的发射过程的内弹道模型和动力学模型能够对某低后坐自动炮的特性进行准确预测。
2)通过对某低后坐自动炮发射动力学特性的分析,表明在保证弹丸初速基本不变的同时最大后坐力减小高达74%,验证了该创新集成的火炮能够有效地协调火炮威力与机动性之间的矛盾。
3)通过对惯性炮闩缓冲簧参数进行的优化匹配设计,表明在不影响系统性能的前提下炮闩最大阻力减小约14.2%,为惯性炮闩轻量化设计提供了参考依据。
