吸湿聚氨酯保温材料导热系数模型研究

2023-08-29王后密

长江科学院院报 2023年8期

王后密,刘超,明锋

(1.中交二公局第四工程有限公司,河南洛阳 471013;2.青海省交控建设工程集团有限公司,西宁 810003;3.中国科学院西北生态环境资源研究院冻土工程国家重点实验室,兰州 730000)

0 引言

在我国寒冷地区,大量的渠道工程均存在不同程度的冻害,主要表现为衬砌板隆起、鼓胀和局部滑塌[1-2]。分析发现,上述冻害主要由渠底土体发生冻胀而造成。针对渠底土体冻胀问题,通常采用铺设保温板的方式来减小土体冻胀[3-4]。尽管保温材料在服役早期能够有效减小渠底土体的冻胀,但由于保温材料自身具有吸湿性,其保温性能随着服役时间的增长而有所下降[5-6]。此外,渠道防渗系统的失效对吸湿过程起到了促进作用,加速了保温性能的劣化。导热系数是表征材料保温性能的核心指标,其大小反映了保温材料的保温性能[7]。因此,开展保温材料的导热机理研究,分析吸湿过程中其导热系数的变化规律,对渠道冻害防治具有重要意义。

保温材料是一种典型的多孔介质材料。确定多孔介质导热系数的方法主要分为3大类：试验拟合法、理论分析法和数值模拟法[8]。试验拟合法是先测试材料在某一状态下导热系数值[9-10],然后利用实测数据拟合出导热系数与某一变量的关系。然而,导热系数与含水率的关系可表示为线性关系[10]、幂函数或者指数关系[11],这说明此方法对特定材料适用性较强,对其他材料的适用性较差[12]。理论分析法则是采用表征体单元方法对模型进行优化,然后使用串联、并联法则求解其等效导热系数[13-14]。这种方法给出的导热系数模型的各参数具有明确的物理基础,且不依赖经验参数,所以此类方法应用较为广泛[15-16]。但是,当多孔介质内部结构复杂时,采用此方法计算导热系数就变得困难[8]。采用有限元等数值模拟计算法,则可更多了解多孔介质内部的传热状况[17]。研究表明,考虑多孔介质微观结构,可以有效降低数值模拟与试验结果之间的误差[7]。相对而言,数值模拟法在处理复杂几何边界时具有一定的优势,不仅可考虑多孔介质内连续相和分散相颗粒的大小和形状,还可描述颗粒之间的接触程度,进而提高等效导热系数预测精度[18]。但该方法所得结果只能以曲线或图表方式给出,无法给出导热系数与材料微结构及各组分体积分数的关系[19]。

本文以广泛使用的聚氨酯保温材料为研究对象,首先测试聚氨酯材料在吸湿条件下的导热系数。然后,基于最小热阻力原理及等效导热系数法则,推导考虑孔隙率及含水率变化的导热系数计算模型。最后,通过与试验结果及已有模型的预测结果进行对比,验证模型可靠性。本研究旨在深化对保温材料在长期吸湿过程中保温性能变化的认识,以期为保温材料改性提供参考。

1 试验过程

1.1 试样制备

试验样品为市售聚氨酯保温材料,其基本物理性质如表1所示。先将保温板制成300 mm×300 mm× 30 mm的试样,并编号称重。然后,将试样放入50 ℃的烘箱中进行烘干。当连续两次测量的试样质量变化率<0.1%时,可认为试样已经干燥。

表1 保温材料基本性质

1.2 试验步骤

为使试样快速达到实验所需的含水状态,将干燥试样置于真空饱和器中,通过控制真空压力和吸水时间,试样则拥有不同含水率。取出试样后,首先擦去试样表面的附着水,然后称取试样质量,并计算其含水率w,即

(1)

式中：m1为干燥试样质量;m2为吸水后某一时刻试样的质量。

为防止水分吸湿或蒸发,将称量后的含水试样采用聚乙烯薄膜包裹。静置96 h以上,使水分在试样内分布均匀。然后依据《绝热材料稳态热阻及有关特性的测定防护热板法》(GB/T 10294—2008)中的测试方法,采用导热系数仪测量不同吸湿条件下保温材料的导热系数(图1)。

图1 导热系数测试仪

1.3 试验结果

图2给出了不同含水率下聚氨酯保温材料的导热系数变化曲线。从图2可知,导热系数与含水率呈正相关关系。当试样质量含水率为14.54%时,其导热系数为0.030 8 W/(m·K),较干燥时增加了24.89%。这是因为在干燥状态时,保温材料内的孔隙由空气填充,传热介质主要是固体骨架,其次是空气。因此,干燥时的导热系数相对较低。聚氨酯保温材料是典型的轻质多孔材料,具有一定的吸湿性[20],当保温材料吸湿后,水分取代空气进入保温材料内部,水分发挥热桥作用,形成以固体骨架、空气及水分混搭的传热通道[7,12]。由于水的导热系数是空气导热系数的20多倍,这就使得聚氨酯保温材料在吸湿后的导热系数大幅增加,保温性能将降低。

图2 聚氨酯导热系数随含水率变化规律

2 模型建立

聚氨酯保温材料包括异氰酸酯、多元醇、发泡剂、外加剂及改性剂等多种组分。当聚氨酯的组分固定,填充气体为空气时,孔隙率是影响其导热系数的关键因素[13]。因此,本文将聚氨酯基质看成一个相,空气看成一个相,将聚氨酯视为一种由基质与空气组成的两相复合材料。先将水分与空气进行复合,再将含湿空气与聚氨酯进行复合,进而研究吸湿状态下的导热性能。

2.1 理论基础

根据最小热阻力法则,热流将选择热阻最小的通道进行热量传递,则此通道的热阻为最小热阻或等效热阻[19]。由傅里叶定律,可得到均质材料热阻与导热系数的关系,即

R=L/(Aλ) 。

(2)

式中：R为等效热阻;L为热流通道长度;A为热流通道面积;λ为材料导热系数。

对于均质体材料,不论单元体的尺度大小,在只考虑热传导时,这种单元体与总体的导热系数相等。因此,复合材料的导热系数λe可通过计算等效热阻Re得到,即有

λe=1/Re。

(3)

2.2 单元体建立

根据聚氨酯保温材料的特点,做出以下假设：

(1)孔隙以相同大小的球体均匀分布于聚氨酯基体中。

(2)由于孔隙的直径远<4 mm,可忽略孔隙内的热对流[21]。

由此,对多孔介质导热系数的研究(图3(a)),就转化成对单元体导热系数的研究(图3(b))。将聚氨酯材料切割成一系列单元体,而每个单元体则是由聚氨酯基体包含着一个孔隙的立方体,如图3(c)所示。

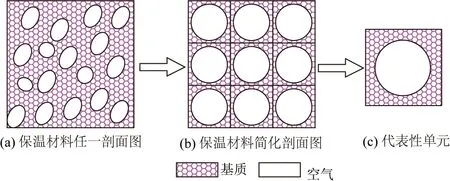
图3 聚氨酯材料导热物理模型

2.3 理论公式推导

为计算单元体等效热阻,将单元体简化成边长为1的正方体,而单元体内的孔隙则简化成球体,如图4(a)所示,α为y轴与OA夹角。热流方向自上而下,把与热流q平行方向的微元体视为一个通道,把与热流垂直方向的微元体视为一个通道,如图4(b)所示。

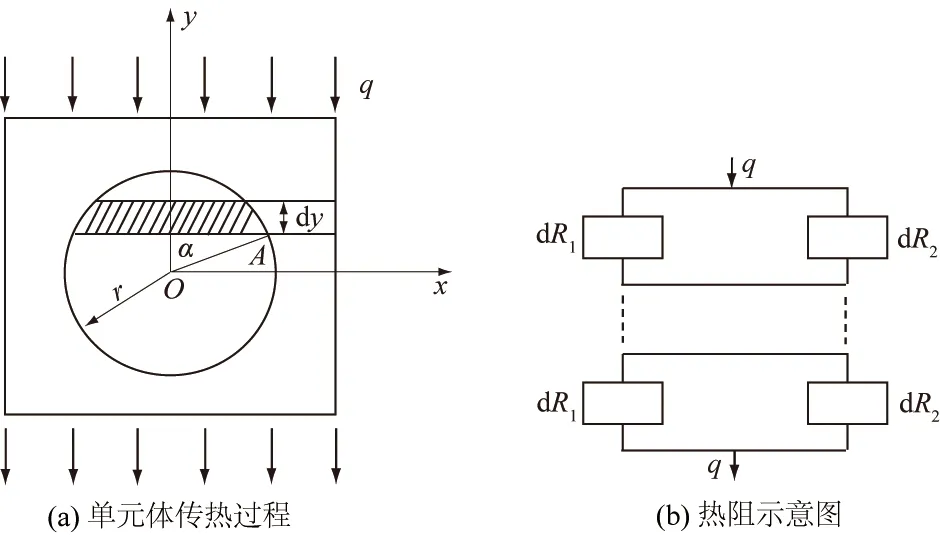
图4 单元体模型的热阻网络

基于上述假设,可将单元体的热阻分成两个通道进行计算：

(1)热流在多孔材料基质内传递时的热阻。

(2)热流在由多孔材料基质和空气组成的通道内传递时的热阻。

对于均质材料(通道1),其热阻R1为

(4)

式中：λ1为基质体的导热系数;r为孔隙半径。

对于通道2,其热阻计算相对复杂。以球体的球心为原点,取y处一厚为dy的微元体,如图4(b)所示,则dy的热阻可看作是截面面积为πr2cos2α的空气热阻与截面面积为1-πr2cos2α的基质热阻的并联。通道2中的微元体热阻dR2为

式中λ3为空气的导热系数。

对式(5)积分,可得通道2的热阻R2为

单元体的总热阻R由通道1的热阻和通道2的热阻构成,即

R=R1+R2。

(7)

依据式(3)和式(7)可以得单元体的导热系数λ为

(8)

式(8)为干燥状态时,保温材料导热系数的计算式。当材料吸水以后,内部的部分空气被水取代,由此可得含湿状态下的导热系数计算式。赋予相应的参数后,就可以通过式(9)计算不同含水率下的导热系数,即

(9)

式中：λ2为水的导热系数;θ为临界角。

对于孔隙率为n的保温材料时,其孔隙球体半径r可表示为

(10)

式中n为孔隙率。

依据三相指标换算,饱和度Sr与质量含水率w存在如下关系,即

(11)

式中：Vw为水的体积;Vv为孔隙体积;ρ0为材料密度;ρw为水的密度;V为材料体积。

2.4 既有导热系数模型

为检验本文模型的可靠性,选取已有导热系数模型进行对比。常用的导热系数模型有[8]：

(1)并联模型,其表达式为

λ=(1-n)λ1+nSrλ2+n(1-Sr)λ3。(12)

(2)串联模型,其表达式为

(13)

(3)Woodside-Messmer(W-M)模型,其表达式为

λ=λ11-nλ2nSrλ3n-nSr。

(14)

在吸湿过程中,吸入的水分将填充保温材料内部孔隙,使得气体和水分体积变化量相等,但符号相反。据此,可得如下表达式,即

d(nSr)=-d(n-nSr) 。

(15)

将式(11)代入式(15)中,有

(16)

若令干燥时(w=0)的保温材料导热系数为λ0,以并联模型(式(12))为例,可得以含水率为变量的导热系数表达式,即

(17)

同理,可得串联模型和几何平均模型在仅考虑含水率变化条件下的导热系数表达式分别为：

(18)

(19)

3 验证与讨论

对于聚氨酯保温材料,其干燥状态下的导热系数λ0为0.024 9 W/(m·K),其基质导热系数λ1为0.480 2 W/(m·K)。水的导热系数λ2取0.58 W/(m·K),密度ρw为1 000 kg/m3,空气的导热系数λ3取0.022 9 W/(m·K)。将上述参数代入预测模型,可获得不同模型预测的导热系数。

3.1 干燥条件下孔隙率对导热系数影响规律

聚氨酯保温材料内部存在大量封闭孔隙,这些微小的封闭孔隙起到了保温隔热作用。然而,封闭孔隙率难以测量。因此,有学者建议采用孔隙率来描述孔隙率对保温材料的导热系数的影响[7]。本文利用孔隙率来求分散相的等效半径,并基于最小热阻力法则建立导热系数模型。从图5可以看出,导热系数与孔隙率表现出负相关关系。当孔隙率从0增加至0.7时,导热系数从0.48 W/(m·K)降低至0.102 2 W/(m·K),降幅高达79.5%。相对而言,空气导热系数远小于聚氨酯基质的导热系数。因此,当孔隙率增大时,空气体积分数增加,使得材料导热系数降低。当保温材料孔隙率为0.78时,其实测导热系数为0.024 9 W/(m·K),计算值为0.024 4 W/(m·K)。导热系数预测值与试验值的相对误差<3%,说明本文模型具有较高的预测精度。

图5 孔隙率对导热系数影响规律

3.2 含水率对导热系数影响规律

聚氨酯保温材料是典型的多孔介质,尽管其固体骨架材料具有憎水性,但仍有一定的吸水性。图6显示导热系数随含水率增大而增大,而且在含水率较大时的增幅更为明显。当外部水分进入保温材料内部,孔隙内的空气逐渐被水分取代。液态水的导热系数比空气导热系数大,使得导热系数与含水率呈正相关关系[22]。由于聚氨酯保温材料中存在大量的酯基,在一定条件下,酯基将发生水解反应,导致分子链断裂而引起聚氨酯硬质泡沫的降解,导致聚氨酯保温材料的开孔率和含水率均增大。此外,开孔率与含水率能够相互促进,加速劣化材料的保温性能。这就意味着保温材料内的含水率达到饱和含水率前,其导热系数将持续增大。

图6 导热系数随含水率变化规律

3.3 不同模型预测结果比较

根据基质、空气和水分的体积比例,利用串联模型、并联模型、W-M模型得到了保温材料导热系数。所有模型预测结果(图7)均表明：含水率增大能导致导热系数增大,但影响程度却有所不同。并联模型导热系数的增速最大,其次是本文模型、W-M模型,增幅最小的是串联模型。并联模型和串联模型的预测结果分别位于试验值的上下边界,这2种模型的预测结果均与试验值存在较大误差。这是因为在实际的传热过程中,并非只有单一的传热通道或方向。所以单一的串联或并联模型将导致较大计算误差。有学者建议采用串联和并联模型相结合的方式确定导热系数[7]。本文采用先局部并联、再整体串联的方式确定导热系数。从计算结果来看,本文模型取得了较好的预测效果(表2)。

图7 不同模型预测下的导热系数变化

表2 导热系数试验值与预测值比较

当含水率在0～14.54%范围时,串联模型的预测结果与实测值最大相对误差为36.84%,本文模型的预测结果与实测值最大相对误差为4.94%。需要注意的是,当含水率<2%时,各模型预测结果与实测值较为接近,此时相对误差较小(表2)。随着含水率的增大,串联模型、并联模型和W-M模型的预测误差也随之增大。以并联模型为例,当含水率为5.33%时,模型计算值与实测值差值为0.001 6 W/(m·K);当含水率增加到14.54%时,其差值变为0.011 4 W/(m·K)。与串联模型、并联模型和W-M模型相比,本文模型对预测聚氨酯保温材料导热系数具有更高的精度。此外,相对于其他导热系数模型,本文模型具有物理意义明确、模型参数容易获取的特点。由此说明,本文提出估算聚氨酯保温材料导热系数的方法是可行的。

3.4 模型优缺点

从导热系数预测值与实测值的对比结果来看,本文模型表现优异,不仅能够反映出导热系数随含水率的变化规律,而且具有较高的预测精度。需要注意的是,不同材料的导热系数对含水率的响应程度有所不同。本文中最大含水率为14.54%,而聚酚醛保温材料的含水率可达200%。因此,本模型能否用于其他材料的导热系数预测还有待进步一研究。此外,虽然本文模型物理意义简单,但计算过程较为复杂,计算量较大。因此,后期将对模型进行优化,以增强其通用性,更能满足工程应用要求。

3.5 保温材料改性建议

当孔隙率确定后,含水率将决定聚氨酯保温材料的导热性能。因此,若能提高聚氨酯保温材料的疏水性,对聚氨酯保温材料的推广应用具有重要意义。为保证聚氨酯材料的长期稳定性,在其分子链上引入了亲水性基团,但这些亲水性集团降低了保温材料的疏水性,进而缩短了保温材料在潮湿环境下的使用寿命。研究结果表明,将聚硅氧烷引入聚氨酯体系中,可有效提高其疏水性和热稳定性[23]。此外,含氟链段的存在不仅可降低表面能,提高材料的疏水性,而且可以减少氟化物的扩散,符合绿色材料制备的要求[24]。