用于玻璃热压印的高温快速均匀加热模块的制造及优化
2023-08-29王鑫龚峰张志辉杨高
王鑫, 龚峰, 张志辉, 杨高*
(1.深圳大学 机电与控制工程学院 深圳市高性能特种制造重点实验室,广东 深圳 518060;2.香港理工大学 工业及系统工程系 超精密加工技术国家重点实验室, 中国香港 999077)
1 引 言
热压印技术可实现高精度微结构的低成本复制,被应用于微透镜阵列、衍射光学元件和菲涅尔透镜等微光学元件的生产中,以满足光学、生物医学、激光辐射及光纤通信等领域的应用需求[1-3]。热压印成形过程是将坯料放入高精度的模具中,经过加热、保温、退火、冷却等步骤,将模具的结构特征复制到坯料上[4]。在热压印过程中,加热模块的加热速率和表面温度分布直接影响热压印的效率和制品的成型精度[5]。因此,高温快速均匀加热模块的开发是微纳热压印技术的一个研究重点。
加热模块的加热速率和温度均匀性与匀热块的材料、结构、发热元件的布局、加热方式等多种因素有关[6-8]。近年来,研究人员一方面尝试了多种加热方法来提高热压印效率,如石墨烯-聚合物复合气体辅助加热、感应加热、激光辐照加热、红外加热等[9];另一方面,通过优化不同位置加热元件的热流密度来提高表面温度分布的均匀性。Chen等[10]利用石墨烯优异的电热特性设计了一种石墨烯-聚合物复合加热器进行热压印,提高了加热效率,但这种石墨烯涂层技术中涂层的低强度和不均匀性会导致结构的不稳定和温度分布的不均匀。Nian等[11]提出了一种感应式热压装置,使用感应加热线圈快速加热平板模具的表面,而不是整个平板模具,提高了加热效率。此外,在感应线圈的中心放置铁氧体材料来解决由邻近效应引起的表面温度不均匀的问题,并提高了表面温度。Kurita等[12]提出将电阻加热方式改为激光加热来提高加热速率,即将玻璃放置在模具上,激光穿过玻璃基板照射到模具上,通过热辐射进行加热。王小权[13]在模压机加热系统的设计中选用短波红外加热管,并对加热管进行半镀金处理来提高加热效率。陈冲[14]设计了一种复合加热系统,使用电磁感应加热模具表面,硅钼棒电阻加热模具内部,实现对模具整体的快速加热。Chen等[15]利用感应加热线圈从内向外加热模具,并利用红外加热管加热模具外表面,两种加热方式共同实现对模具的快速协同加热,并改善其表面温度分布的均匀性。史春彦等[16]设计了一种具有夹层结构的加热模块,通过增加面导热率高的夹层材料来加快热量的传导速率,使加热模块表面温度更均匀。Li等[17]把模具的加热系统简化为单个加热单元进行热响应分析,以电加热元件规格和位置为优化设计参数,所需加热时间和模具表面温差为热响应指标,建立加热单元多目标优化模型,得到了加热单元的优化设计参数组合。刘锋等[18]在确定加热管道布局的情况下,研究不同热流密度对模具型腔表面温升速率和温度均匀性的影响,发现型腔表面温度和温度分布均匀性是一种竞争关系。本研究团队[19]开发了基于氮化硅陶瓷加热片的快速加热模块,其结构简单,且最高温度可达800 ℃,加热速率为300 ℃/min。
为了在保持高加热速率的同时,进一步提高加热模块的表面温度分布均匀性,本文设计制造高温快速均匀加热模块,并搭建加热测试平台。然后,比较相同工艺条件下的有限元仿真结果和实验结果来验证仿真模型的准确度。在此基础上,利用正交试验法进行多因子多水平分析,实现快速加热模块的整体结构优化,以提升其加热性能。
2 实 验
2.1 氮化硅陶瓷加热片加热性能测试
本文开发加热模块的发热元件为氮化硅陶瓷加热片。氮化硅陶瓷加热片是以氮化硅陶瓷为基体,钨丝为发热源,将钨丝埋在氮化硅基体中通过热压烧结工艺形成一体,再经过磨削加工,焊接导线制成。为方便后续对加热模块的设计制造及优化,需对发热元件本身的加热性能进行测试。由图1(a)可知,陶瓷加热片通电加热时,中间区域呈亮白色,温度较高,故在对应位置均布6个测温点D1~D6。利用图1(b)所示的实验装置对陶瓷加热片的表面温度进行测量,即热电偶从底部穿过云母片并固定于陶瓷加热片下表面。这种测量装置可以减少周围环境的干扰,从而获得更准确的温度测量结果。
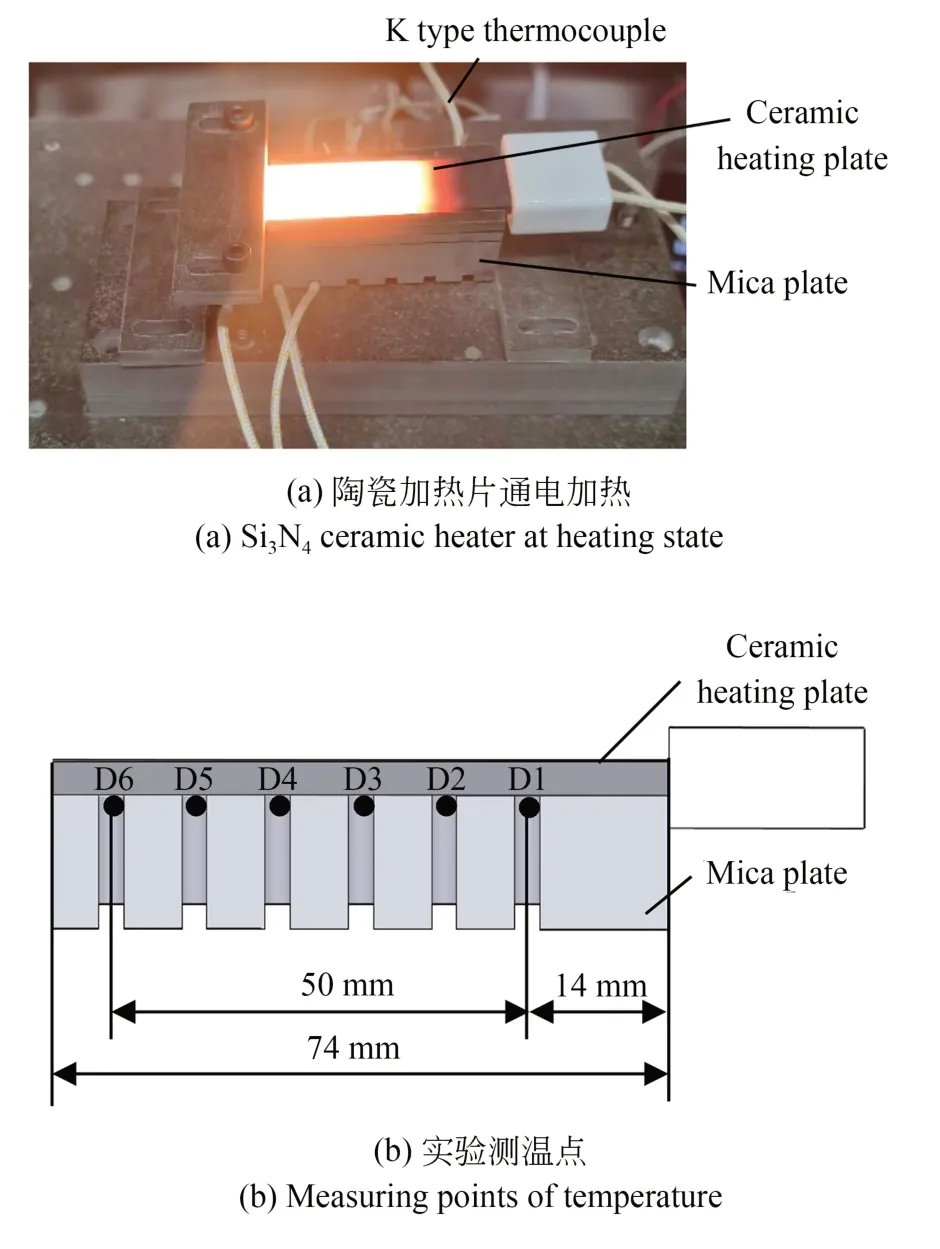
图1 陶瓷加热片表面温度测量装置Fig.1 Measurement setup for surface temperature of ceramic heater
实验过程中,对陶瓷加热片施加额定220 V的直流电来测试其最大加热速率和能达到的最高温度。图2为施加220 V电压时陶瓷加热片上各点温度随时间的变化曲线。中心点D2在150 s左右温度能达到1 000 ℃,加热速率极快,满足高温热压印的快速加热需求。但是,陶瓷加热片表面的温差较大,中间点D2,D3,D4的加热速率较快,边缘点D1,D5,D6的加热速率较慢,即加热区域主要集中在中间区域。在热压印时,不均匀的温度分布会使成型元件产生残余应力。因此,需要在陶瓷加热片表面包覆高导热材料,如纯铜,使传热更均匀。如图3所示,本文将纯铜覆盖在陶瓷加热片中间的主要加热区域,从而在不明显降低加热效率的条件下显著提高表面温度的均匀性。
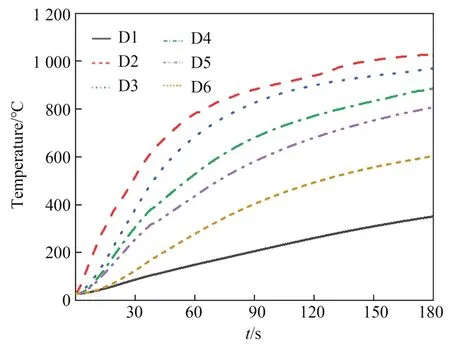
图2 陶瓷加热片上各点温度随时间的变化曲线Fig.2 Temperature histories of various points on surface of ceramic heater
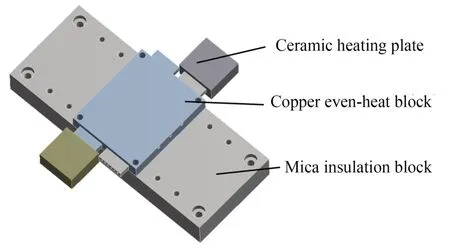
图3 加热模块的几何模型Fig.3 Geometric model of heating module
2.2 实验装置
如图4所示,实验装置主要由加热模块和温度测量模块组成。加热模块使用尺寸为60 mm×60 mm×10 mm的纯铜匀热块。匀热块中间开设有对称的2个方形槽,用来放置氮化硅陶瓷加热片(见图5(a))。匀热块下面的隔热块材料为云母。温度测量模块利用一台HIOKI LR8450数据采集仪和多根K型热电偶来记录加热过程中的温度信号。

图4 氮化硅陶瓷加热实验装置Fig.4 Experimental devices of Si3N4 ceramic heater
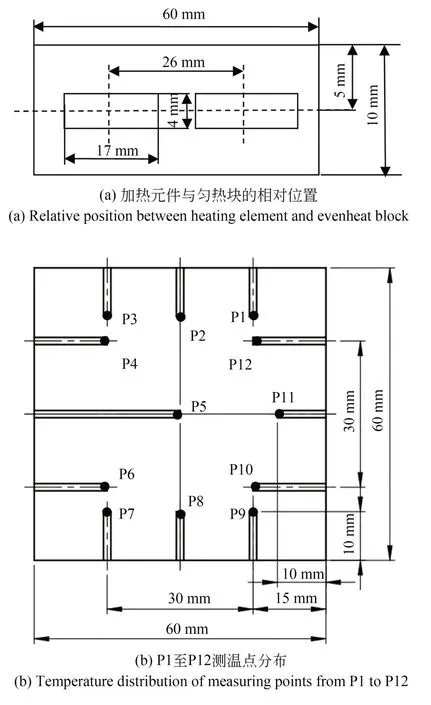
图5 均热块结构Fig.5 Structure of even-heat block
将K型热电偶插入匀热块侧边深孔进行温度测量,热电偶与匀热块上表面的距离为1.5 mm。热电偶的具体安装位置如图5所示,可测量P1至P12点的温度。将匀热块作为一个“温度传感器”,能够实时反映匀热块表面温度的均匀性。
2.3 加热阶段传热过程分析
当给陶瓷加热片通电时,电流通过陶瓷加热片中的钨丝产生热量Q,热量沿径向从陶瓷加热片向周围传递。由于陶瓷加热片只有少部分直接与匀热块内表面接触,且存在着空气层,陶瓷加热片产生的热量一部分通过固体热传导的形式传递给匀热块,一部分通过空气传递给匀热块,另一部分通过热辐射传递给匀热块,还有一部分由空气层沿轴向的对流所损耗[20]。并且,加热模块还以热对流与热辐射的方式与周围环境进行热交换,具体传热过程如图6所示。

图6 加热阶段传热过程分析Fig.6 Analysis of heat transfer in heating stage
根据热传递过程的能量守恒定律,加热过程中的热传递可表示为[20]:
式中:Qh为陶瓷加热片输出的热量;Qm为匀热块吸收的热量;Qi,Qr分别为匀热块表面和周围环境通过热对流和热辐射交换的热量;Qc为匀热块向云母传递的热量;Qf是储存在加热元件内部的热量。
为研究热传导过程各因素对加热速率的影响,取Δt来分析。假设匀热块的初始温度为平均温度为加热Δt后,匀热块的平均温度为
式中:Pi是陶瓷加热片在不同时刻输出的功率;Δt是陶瓷加热片从室温加热到指定温度的时间;cm,ρm,Vm分别为匀热块的比热容、密度和体积;hm,Am分别为匀热块外表面与空气的热对流系数和接触面积分别为加热结束时匀热块外表面温度和周围环境温度;εm,σ分别为匀热块的发射率和斯特藩-玻尔兹曼常数。
根据上述分析,联合式(2)~式(5)得:
由式(6)可知,为提高快速加热模块的加热速率,可通过增大P,或减小cm,ρm,Vm,Qi,Qr,Qc,Qf来实现。功率P由发热元件本身的规格决定。cm,ρm是匀热块的物性参数,Vm代表匀热块的体积。因此,在相同的输出热量Qh下,选择低比热容的纯铜匀热块,并减小匀热块体积,温度能更高。加热实验在手套箱内进行,以减少Qi,Qr的影响;利用低热导云母片对匀热块进行隔热处理,可以减小Qc;Qf反映的是陶瓷加热片本身储存的热量,减少Qf实际上就是实现陶瓷加热片与匀热块之间热量的迅速转移,即减小匀热块与陶瓷加热片之间的安装间隙并改善表面的接触状态。其中Qi,Qr,Qc,Qf相对于Qh和Qm较小[20],在加热期间对模具温度变化的影响比较小。在均热块材料、加热元件功率及加热环境一定的情况下为常量,从式(6)可知在相同加热时间内,调控均热块体积Vm能显著影响加热模块的加热效率。
2.4 加热实验设计
为了避免外界环境干扰,所有实验均在手套箱内进行。本研究进行恒电压加热实验:以恒定220 V电压对加热模块加热,各点温度由测温仪记录,采样间隔为1 s,每组实验重复3次,取其平均值作为最终结果。
2.5 实验结果及分析
为验证实验的重复性,比较5次实验中P5测温点加热300 s的温升曲线,如图7所示。5次实验的温升曲线基本一致,实验具有很好的重复性。
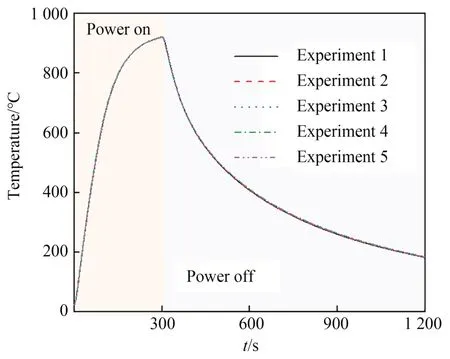
图7 测温点重复性验证Fig.7 Verification of repeatability of temperature measurement
由图7可知,加热前180 s温升速率很快,故选取加热180 s时匀热块的表面温度进行研究。图8为恒电压加热180 s实验中匀热块测温点的温度曲线。在恒定220 V电压下,加热180 s时匀热块的表面温度可达840 ℃,但各点温差为14.5 ℃,温差较大,故需要对匀热块的表面温度进行优化。
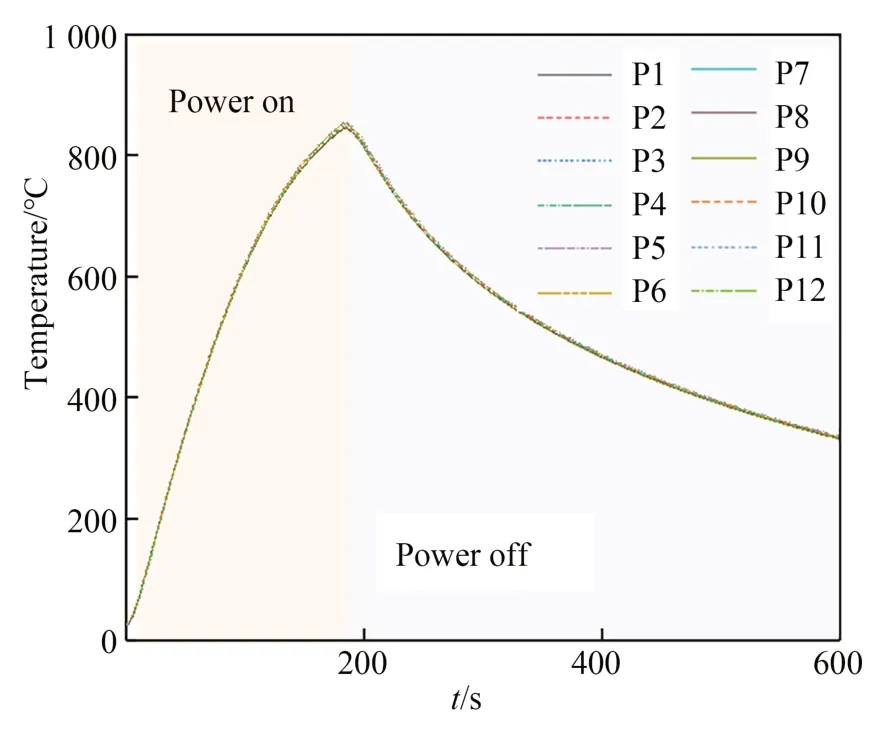
图8 P1至P12测温点恒电压加热180 s的温升曲线Fig.8 Temperature histories of measurement points from P1 to P12 in 180-second constant voltage heating test
3 温度场热响应分析
本文采用ANSYS Workbench软件来模拟快速加热模块的瞬态传热过程。将有限元仿真得到的温升曲线与实验中相同位置的温升曲线进行对比,验证仿真模型的准确性。
3.1 有限元分析模型
图3为快速加热模块瞬态热分析的几何模型。为了更好地分析加热过程的温度场,对模型进行如下的简化与假设:
(1)假定陶瓷加热片释放的热量都被匀热块所接收,即不计热损失;
(2)忽略匀热块与陶瓷加热片之间的安装间隙;
(3)假设加热模块中的材料为各向同性,且各材料的热物性参数如表1所示;
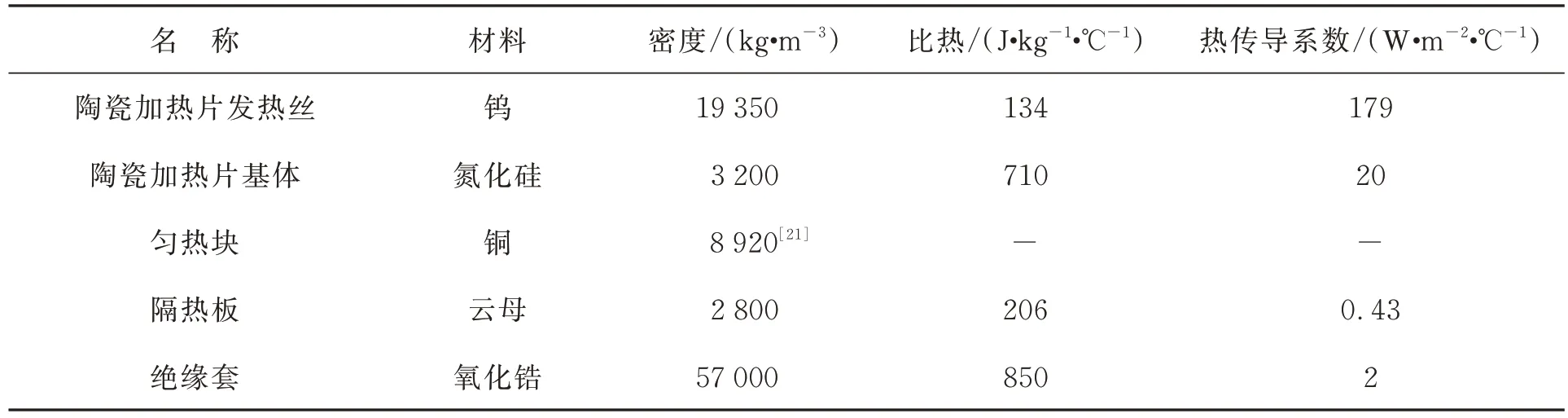
表1 加热模块各材料的热物性参数[22-23]Tab.1 Thermophysical parameters of each material of heating module
(4)考虑纯铜匀热块的导热系数、比热容随温度不断变化[21](见图9)。
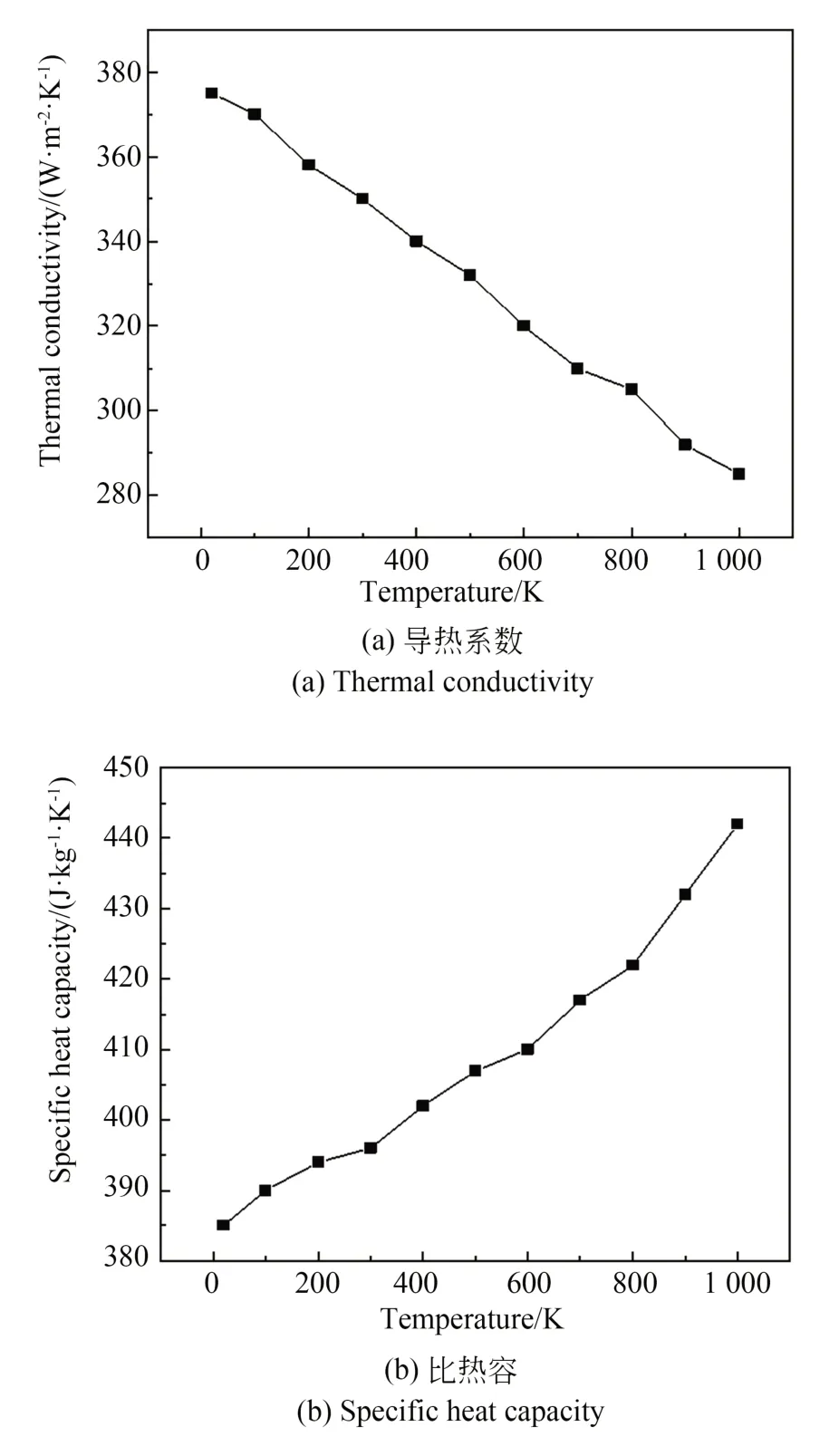
图9 铜的热物性参数Fig.9 Thermophysical properties of copper
3.2 有限元网格划分
在有限元分析中,划分网格的结构和疏密程度直接影响到计算结果的精度,因此需要控制网格划分的质量。这里主要研究匀热块的表面温度,故使用六面体网格,并将匀热块表面及陶瓷加热片的网格进行细化(见图10)。

图10 加热模块的网格划分Fig.10 Mesh of heating module
3.3 初始与边界条件的确定
匀热块初始温度和空气温度均等于实际环境温度,为25 ℃。根据实验测量的加热功率数据,设置陶瓷加热片的输入功率为900 W。空气与纯铜匀热块的对流传热系数在2~25 W/(m2·℃)之间[24],本仿真将对流传热系数设为15 W/(m2·℃)。在设置热辐射参数时,考虑到铜在高温下易氧化,取其发射率为0.8。
在微观尺度上,铜匀热块与陶瓷加热片的表面接触仅发生在一些离散微凸体上。这种不完全界面接触会导致热流收缩,影响界面传热。界面接触热阻的数量级通常在1×10-4到1×10-3(m2·℃)/W[25-27]。本次实验中匀热块与陶瓷加热片之间无接触压力,并且还有一定的装配误差,所以界面传热系数取较小值,为2 000 W/m2。加热模块各零件之间采用绑定接触,传热方式为热传导。建立传热分析模型,设置总加热时间为180 s,选择固定增量模式,每一步的加热时间为10 s。
3.4 仿真结果分析
图11为匀热块在恒定220 V电压下加热180 s后的表面温度分布,可以看出,匀热块中间位置的表面温度高于边缘位置的表面温度。这是因为两个氮化硅陶瓷加热片同时向纯铜匀热块传递热量,故匀热块中间位置热量更大,即温度更高。另一方面,匀热块侧面与空气对流换热,存在热量损失,故边缘位置的表面温度较低。

图11 恒电压加热180 s时匀热块上的表面温度分布Fig.11 Temperature distribution on upper surface of even-heat block under constant-voltage heating for 180 s
3.5 模型验证
图12对比了匀热块在恒电压加热实验与仿真中的温升曲线,发现两者基本吻合。但是,在初始加热阶段,仿真结果与实验数据稍有偏差,有两个原因:(1)匀热块迅速升温,而热电偶响应速度有限,从而使温度测量数值偏低;(2)陶瓷加热片与匀热块界面存在间隙,影响陶瓷加热片与匀热块之间的热量传递,导致实验数据小于仿真结果。随着温度的不断升高,陶瓷加热片的功率降低,匀热块升温速率有所下降,则热电偶的测量温度准确性提高。高温下陶瓷加热片和匀热块产生热膨胀,减小界面间隙,所以中间段测量温度略微大于仿真温度。但是,随着温度的进一步升高,从匀热块传递到隔热板的热量明显增加,实验测量温度逐渐低于仿真值。
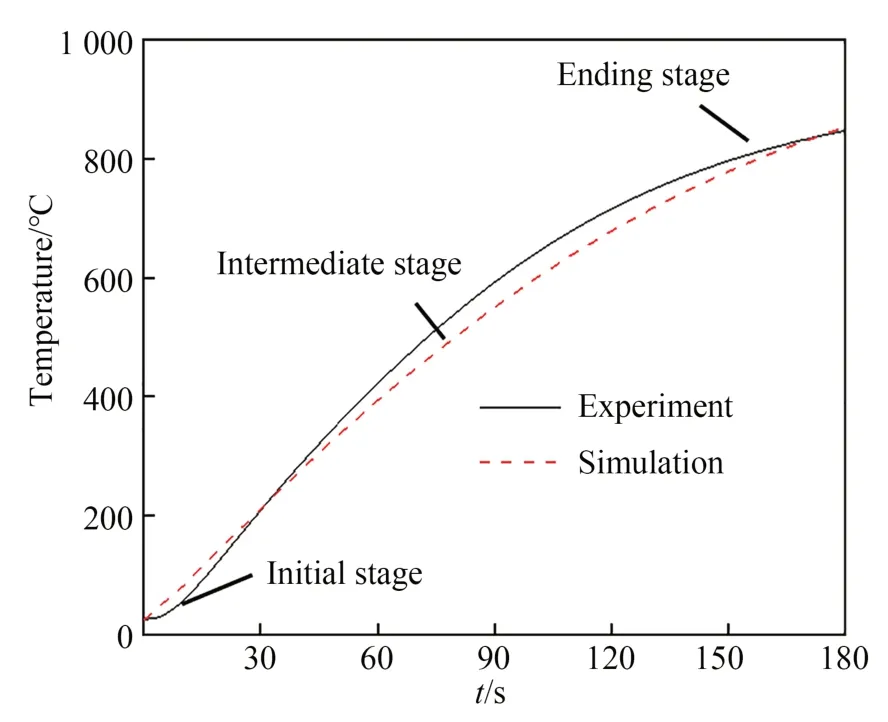
图12 仿真与恒电压加热实验结果对比Fig.12 Comparison of simulation and constant-voltage heating experimental results
将恒电压加热180 s后匀热块各测温点的温度数据和有限元仿真结果进行对比,如图13所示,发现有限元模拟的最高温度为853.88 ℃,最低温度为837.95 ℃,平均温度为847.84 ℃,而实验最高温度为847.2 ℃,最低温度为832.7 ℃,平均温度为840.78 ℃。对于相同测温点,有限元仿真结果与实验测量结果比较接近,相差仅为7.06 ℃,从而进一步验证了有限元仿真模型的准确性。
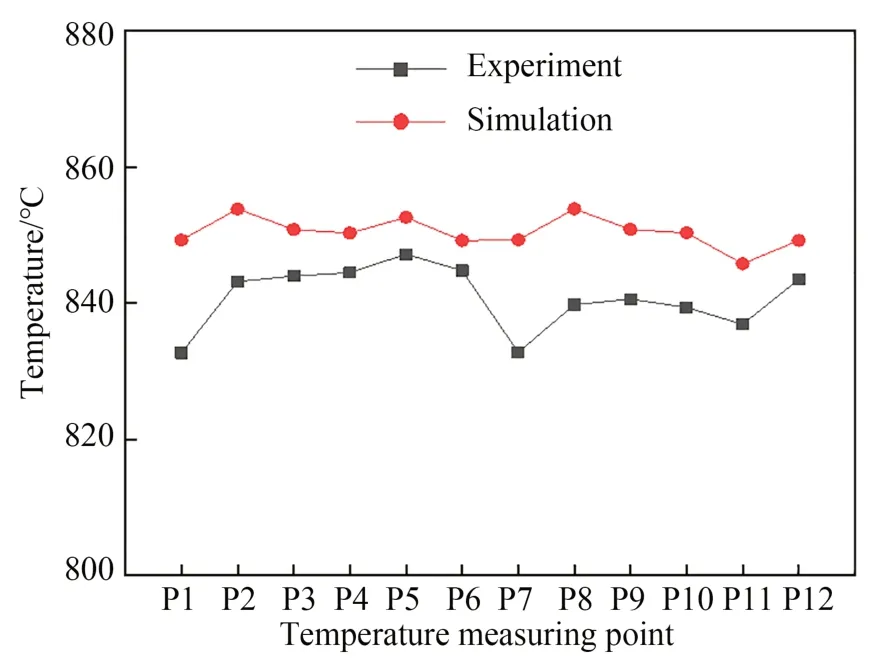
图13 加热180 s时仿真与实验结果对比Fig.13 Comparison of simulation and experimental results when heating for 180 s
4 优化设计
由上述实验可知,匀热块表面的整体温差在14.5 ℃,因此需要对匀热块的表面温度分布进行优化。由式(6)及文献调研[8]可知,可通过微调均热块的体积以及陶瓷加热片的安装位置这两大主要因素来分析它们对匀热块加热效果的具体影响。
4.1 试验因素与优化目标
图14为加热元件位置示意图。将匀热块宽度W、两陶瓷加热片间距X、匀热块厚度D、加热片与匀热块上表面距离H作为正交试验的水平因素。每个因素考虑5个水平值,利用L25(56)正交表设计正交试验(见表2)。
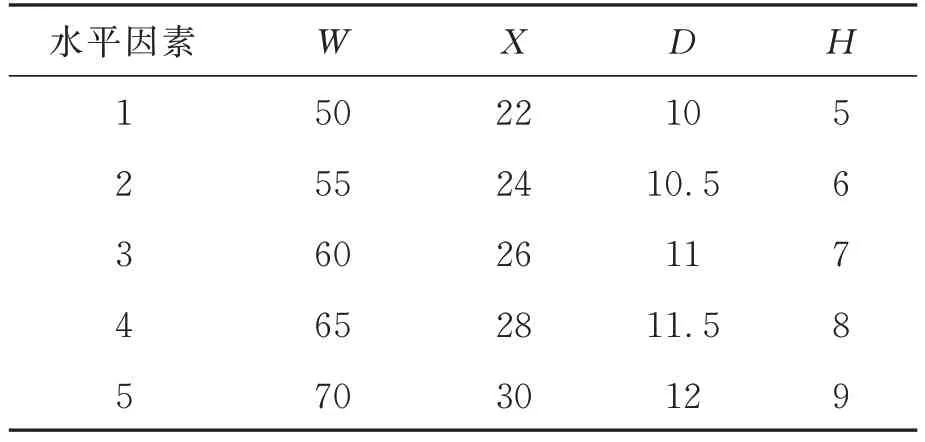
表2 因素水平表Tab.2 Factors and their levels(mm)
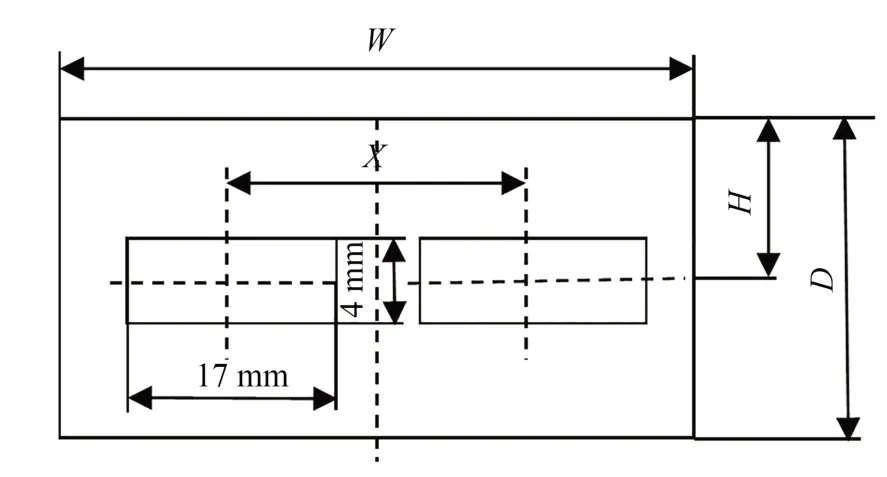
图14 因素的几何含义Fig.14 Geometric meaning of factors
此加热模块主要面向微纳热压印应用,以加热速率和匀热块表面温度的均匀性为优化目标。为保证热压印的成形效率和产品质量,加热速率越快越好,温度分布越均匀越好。采用瞬态传热分析,模拟恒电压加热180 s后匀热块的表面温度,计算其加热速率,并利用表面的最高温度与最低温度之差来描述温度均匀性。试验结果如表3所示。

表3 正交试验结果Tab.3 Orthogonal test results
4.2 正交试验结果分析
利用极差分析法[28]对试验结果进行分析,计算出各因素的均值和极差(见表4),以此判断各因素的主次关系和最优组合。

表4 试验结果分析Tab.4 Analysis of results
4.3 加热速率的影响因素分析
在恒定的加热时间内,匀热块表面所达到的平均温度可以反映其加热速率。由表3可知,匀热块表面平均温度最高的是1号试验的因素组合:W1X1D1H1,即匀热块宽50 mm、陶瓷加热片间距22 mm、均热块厚度10 mm、陶瓷加热片与匀热块上表面的距离为5 mm。施加恒定220 V电压加热180 s后,匀热块表面温度可以达到944.39 ℃,加热速率达306 ℃/min。
图15表明,两陶瓷加热片间距X、加热片与匀热块上表面距离H对加热速率基本没有影响。但是,增加匀热块宽度W和厚度D会显著降低加热速率。这是由于匀热块体积增大,在相同的输入功率下单位体积得到的热量减少;而且匀热块对流面和辐射面的增大导致热量损失增加。因此,加热速率随着匀热块宽度W和厚度D的增大而变小。

图15 各因素对加热速率的影响Fig.15 Influence of various factors on heating rate
通过表4中的极差R可知,影响加热速率因素的主次关系为匀热块宽度W、厚度D、两陶瓷加热片间距X、加热片与匀热块上表面距离H。而且,匀热块平均温度最高的最优组合是W1X3D1H3,即取W=50 mm,X=26 mm,D=10 mm,H=7 mm。
4.4 温度均匀性的影响因素分析
匀热块表面温度均匀性最好的是5号试验的因素组合:W1X5D5H5,即匀热块宽50 mm、陶瓷加热片间距30 mm、均热块厚12 mm、陶瓷加热片与匀热块上表面的距离为9 mm。图16表明,匀热块宽度W减小,两陶瓷加热片间距X增加,或均热块厚度和加热片与匀热块上表面距离H取中间值,可提高匀热块表面温度的均匀性。
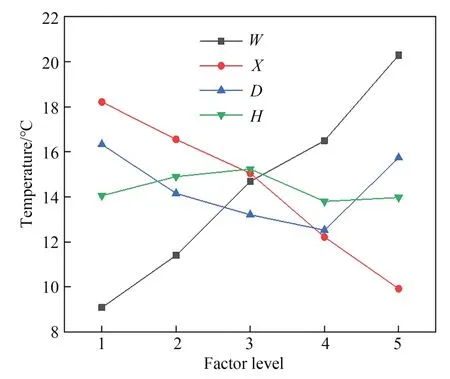
图16 各因素对温度均匀性的影响Fig.16 Influence of various factors on temperature uniformity
由表4可知,影响温度均匀性主要因素的主次关系为匀热块宽度W、两陶瓷加热片间距X、均热块厚度D、加热片与匀热块上表面距离H。匀热块表面温度均匀性的最优组合是W1X5D4H4,即取W=50 mm、X=30 mm、D=11.5 mm、H=8 mm。上述所有试验的加热速率足够快,满足玻璃快速热压印的要求,因此均热块优化结构取温度均匀性最好的参数组合。
4.5 实验验证
图17(a)为有限元模拟仿真结合正交试验进行优化设计得到的匀热块结构。各测温点位置如图17(b)所示。对结构优化后的匀热块进行恒电压加热测试,P1至P12测温点的温度曲线如图18所示。由图可知,在恒定220 V电压下,将匀热块从25 ℃加热到600 ℃需95 s左右,中低温段升温速率可达363 ℃/min;从600 ℃加热到850 ℃需85 s左右,高温段的升温速率为176 ℃/min;在断电情况下,加热模块从850 ℃冷却到500 ℃仅需190 s左右,具有较快的冷却速率。
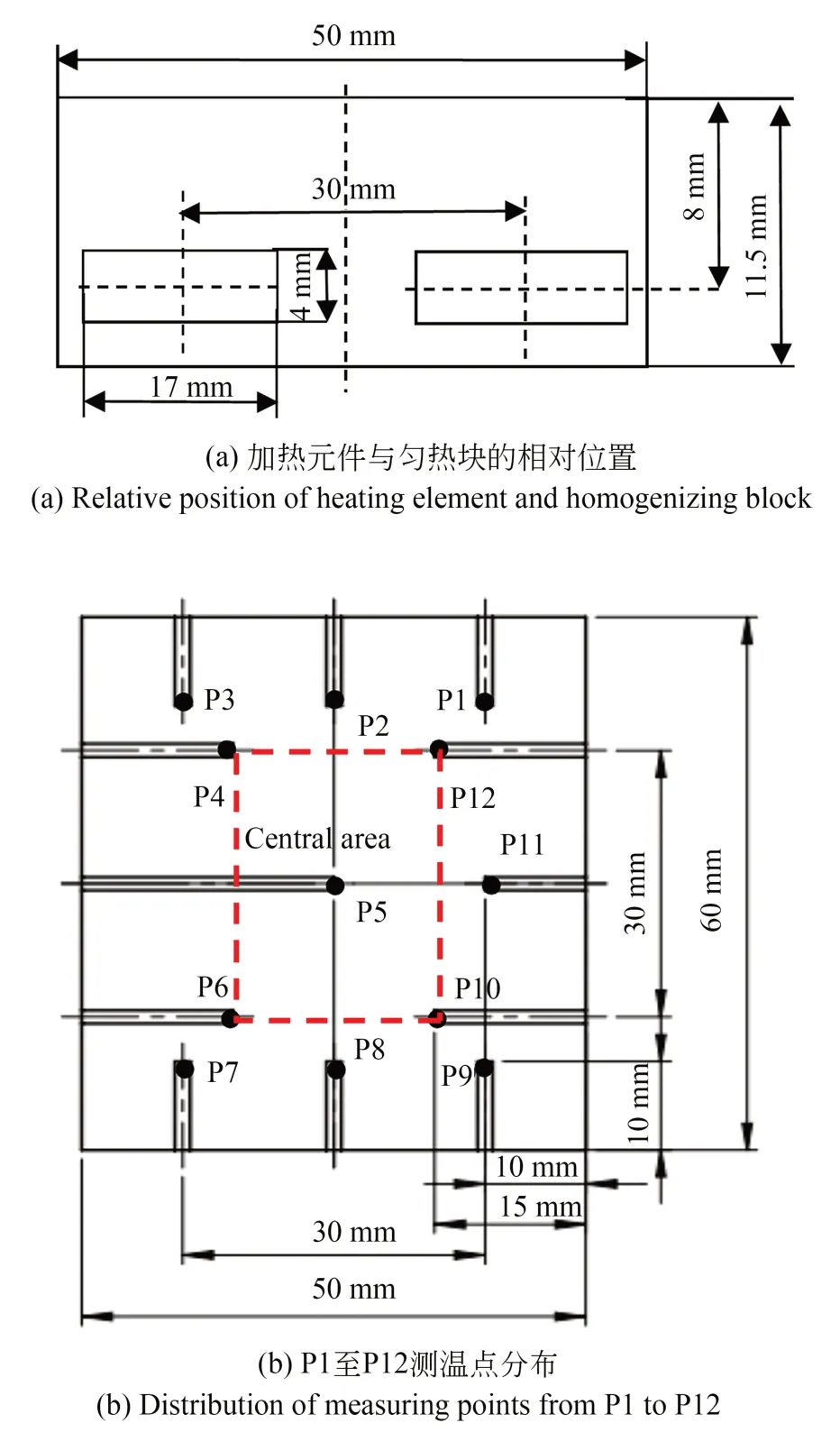
图17 均热块优化结构Fig.17 Optimized structure of even-heat block
在相同的实验条件下,对结构优化前后的匀热块恒电压加热180 s,比较其表面各测温点温度(见图19)。实验结果表明:优化后的匀热块各测温点的平均温度为844.45 ℃,最高温度为850.5 ℃,最低温度为839.8 ℃,温差为10.7 ℃。优化后的匀热块温差由14.5 ℃降低至10.7 ℃,表现出更好的表面温度均匀性,从而验证了有限元仿真结合正交试验进行优化设计的合理性。
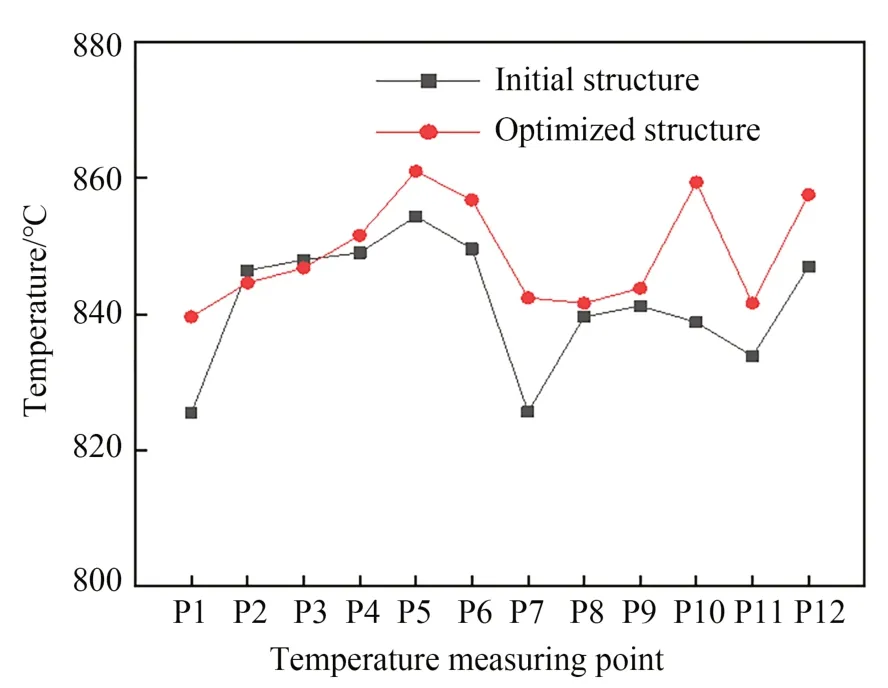
图19 优化前后温度均匀性对比Fig.19 Comparison of temperature uniformity before and after optimization
5 快速加热模块的热压印应用
5.1 温度的精准控制
在热压印过程中,温度准确性对保证玻璃元件的形状精度极其重要。因此,需要对加热模块的温度进行精准控制。温控系统采用智能PID控制,通过驱动温控仪中固态继电器的通断,控制可调直流稳压电源,调整发热元件的输入功率,从而实现温度控制。
使用具有高精度自整定功能的宇电AI-526P型智能温控仪,将均热块中心点P5作为控温点,以最大速率加热到700 ℃,然后恒温一段时间。利用上位机软件导出P5点的温度历史数据,同时利用测温仪记录其余各点的温度历史数据。
图20为控温加热实验中各测温点的温度曲线。由图可知,实验温度曲线与设定温度曲线基本一致,且温度波动在0.3 ℃以内。对恒温阶段的实验温度曲线进行局部放大(见图20(b)),发现匀热块温差在7 ℃以内。特别地,用于热压印的20 mm×30 mm中心区域的温差在2 ℃左右。
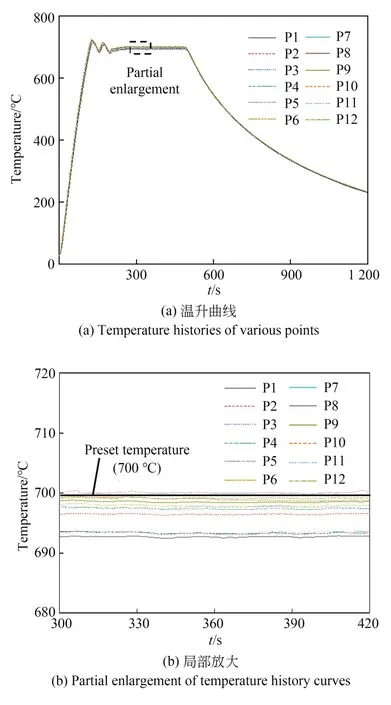
图20 控温加热700 ℃Fig.20 Heating to 700 ℃ under control
控温加热实验结果表明:加热模块的实测温度与温控系统的设定温度基本一致,温控精度能满足低熔点玻璃[29](转化点小于600 ℃)和部分高熔点玻璃的成形需求。此外,在保证控温精度的同时,加热速率快且表面温度分布均匀性好,能很好地满足玻璃快速热压印的成形需求。
5.2 热压印装置
将优化设计与制造的快速加热模块安装在图21所示的热压印装置中,可用于玻璃微纳光学元件的高效制造。该装置由精密加载模块、快速加热模块和多轴运动平台组成。其中,精密加载模块实现压印力的精确调整;加热模块实现快速均匀加热;多轴运动平台实现玻璃坯料的精确定位。在快速加热模块与多轴运动平台间放置云母板,大幅度减少热量向运动平台传递,以保证设备正常运行。
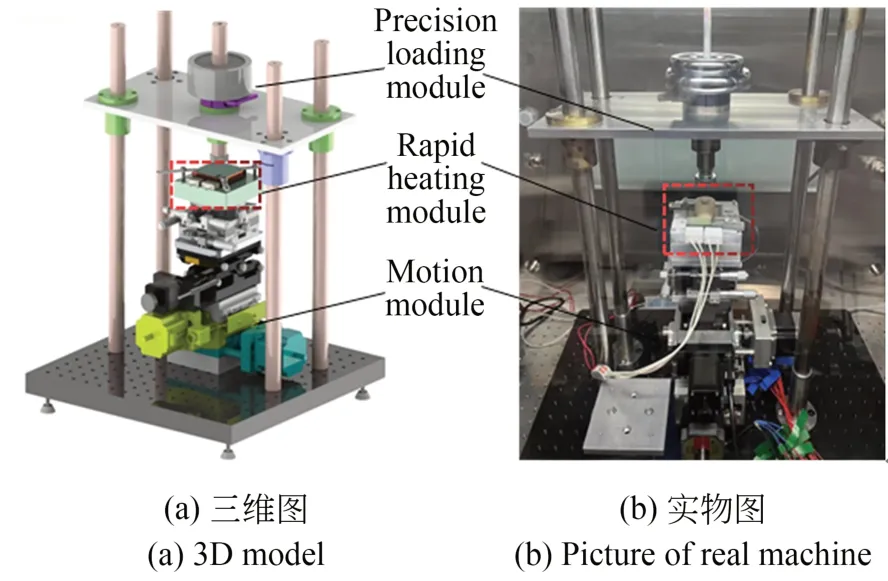
图21 热压印装置Fig.21 Hot embossing machine
5.3 热压印结果
为防止零部件的高温氧化,将热压印装置放置在密封的手套箱内,并提供氩气氛围。通过优化热压印的工艺参数,将碳化硅模具表面的微结构高效精确地复制到N-BK7玻璃表面。图22(a)~22(c)比较了碳化硅微沟槽阵列模具和玻璃光栅元件的表面形貌。模具微沟槽的深度为4.745 μm±3.3 nm,玻璃表面微沟槽的高度为4.744 μm±1.3 nm,特征复制率达99.9%。图22(d)~22(f)展示了碳化硅微孔阵列模具和玻璃微柱阵列的表面形貌。模具微孔的深度为4.686 μm±1.8 nm,玻璃表面微柱的高度为4.675 μm±9.1 nm,特征复制率达99.8%。
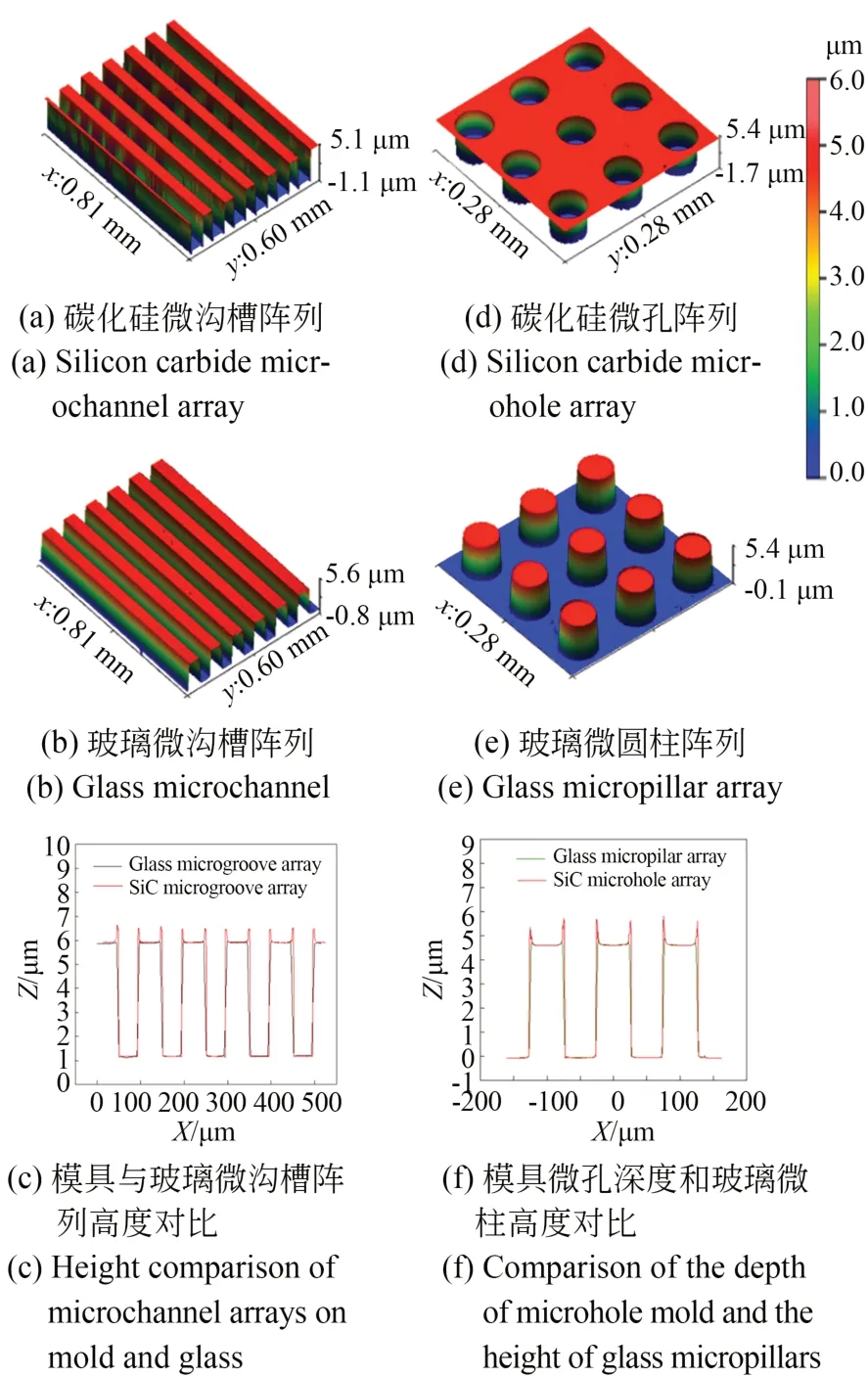
图22 碳化硅和玻璃的微沟槽和微孔阵列表面形貌Fig.22 Surface topography of silicon carbide mold and glass microstructure arrays
6 结 论
本文设计制造了一种基于氮化硅陶瓷加热片的加热模块,并搭建了加热测试平台。建立加热模块有限元模型,进行实验验证后,利用正交试验方法优化加热模块中发热元件的位置分布参数,如匀热块宽度、两陶瓷加热片间距、匀热块厚度、加热片与匀热块上表面距离。开展恒电压加热实验,利用嵌入匀热块表面的12根热电偶实时监测其表面温度。在恒定220 V电压下加热180 s时,匀热块表面温度可达840 ℃,温差为14.5 ℃。将有限元仿真与实验结果进行对比,发现两者比较接近,从而验证了有限元模型的准确性。以匀热块尺寸和发热元件位置分布为优化变量,加热模块的加热速率和表面温度分布均匀性为优化目标,结合有限元仿真和正交试验方法,对加热模块结构进行优化。对结构优化后的匀热块进行220 V恒电压加热测试。实验表明,从25 ℃加热到600 ℃需95 s左右,中低温段升温速率可达363 ℃/min;从600 ℃加热到850 ℃需85 s左右,高温段升温速率为176 ℃/min。而且,加热180 s时,优化后的匀热块温差由14.5 ℃降低至10.7 ℃,表现出更好的表面温度均匀性,从而验证了有限元仿真结合正交试验进行优化设计的有效性。设计了精密温控系统,控温加热700 ℃时,实测温度与设定温度基本一致,且温度波动在0.3 ℃以内。尤其,匀热块中心20 mm×30 mm区域温差在2 ℃左右,能很好满足玻璃热压印的成形需求。利用自主设计制造的快速加热模块和精密温控系统搭建高温热压印装置,成功地在高软化点玻璃(如N-BK7玻璃)表面成形出高质量微光栅与微圆柱阵列,验证了快速加热模块在玻璃微纳结构元件热压印成形的应用。
