水冷燃料电池空气供给系统控制策略研究

解同辰,肖铎

(1.浙江大学控制科学与工程学院,浙江 杭州 310027;2.浙大城市学院,浙江 杭州 310015)

全球变暖、能源短缺、环境污染是困扰人类发展的三大问题,中国做出了“碳达峰、碳中和”的双碳承诺,氢能等清洁能源的大量使用是解决上述问题有效途径。质子交换膜燃料电池(Proton Exchange Membrane Fuel Cell,PEMFC)是一种不经过燃烧将氢能直接转化成电能的装置,以质子交换膜燃料电池作为动力源的氢燃料电池汽车是汽车产业重要的发展方向。水冷质子交换膜燃料电池的空气供给系统具有模型复杂、高度非线性、强耦合、多参数、多变量等特点,选取合适的控制策略可以有效地提高燃料电池系统的输出功率和能源效率。

陈雪兰[1]设计了基于线性变参数模型的预测控制算法对过氧比进行调节,验证了在负载电流大范围变化时算法的有效性。王凡[2]提出反馈线性化控制和基于二阶滑模的串级控制两种策略,实现对过氧比的控制,通过仿真对比得出反馈线性化算法控制效果更优的结论。胡佳丽[3]设计了线性最优控制和二阶滑模超螺旋非线性控制两种算法,实现了对过氧比期望值的准确跟踪,并减少了空压机功率消耗。Ma等[4]将稳态控制、前馈控制和误差反馈控制相结合设计了非线性三步控制器,实现了在负载电流快速变化的情况下将过氧比调节至期望值。雷宗坤[5]设计了基于自抗扰控制的流量-压力动态解耦控制器,通过控制空压机转速和背压阀开度来实现对阴极进气质量流量和进气压力的解耦控制。Liu等[6]设计了扩张状态观测器估计未知扰动,使用反推法设计控制律实现了快速调节电堆阴极压力到期望值。以上文献主要集中于对过氧比或电堆阴极压力单一输出的控制研究,缺乏对同时控制二者的多输出的研究。

本研究建立面向控制的空气供给系统四阶非线性状态空间模型,设计微分观测器估计电堆阴极压力,提出基于反馈线性化的滑模自抗扰控制策略,实现对阴极压力和过氧比期望值的跟踪控制,并仿真验证控制策略的有效性和鲁棒性,因此研究电堆阴极压力和过氧比之间的协同控制具有重要的意义。

1 燃料电池空气供给系统建模

燃料电池气体供给系统由氢气供给子系统和空气供给子系统两部分组成,系统结构如图1所示。空气供给系统由空气压缩机、空气供给管道、冷却器、增湿器、电堆阴极、回流管道和背压阀等装置组成[7]。本研究采用机理建模和经验建模相结合的方法,建立面向电堆阴极压力和过氧比控制的空气供给系统多输入多输出模型。

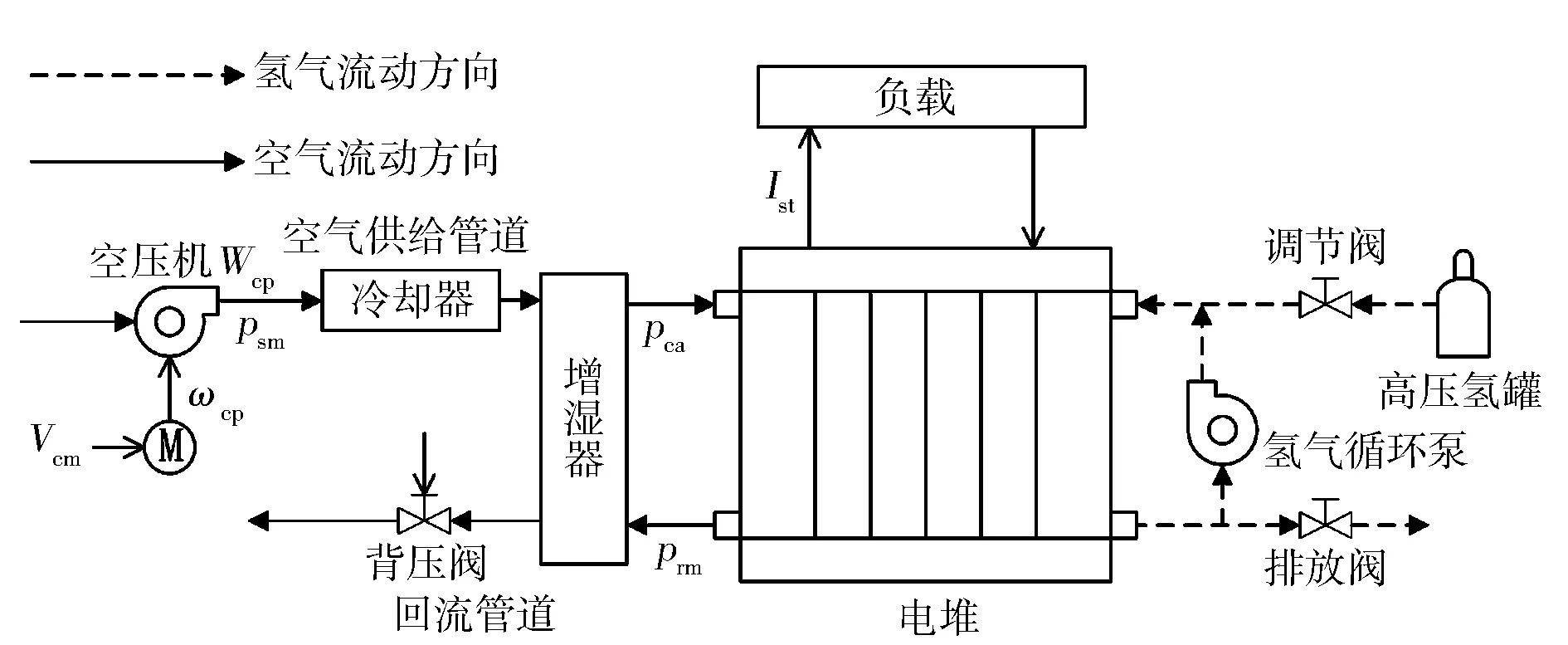
图1 燃料电池气体供给系统结构

1.1 空气压缩机模型

空气压缩机的动态响应模型为

(1)

式中：Jcp为空压机转动惯量;ωcp为空压机转动角速度;τcm和τcp为空压机电机的驱动力矩和负载力矩,计算公式分别见式(2)和式(3)。

(2)

(3)

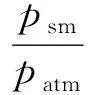
(4)

式中：qi(i=1,2,…6)为空压机模型常数。

1.2 管道模型

空气供给管道气体压力变化表达式为

(5)

式中：Ra为空气气体常数;Ma为空气摩尔质量;Vsm为空气供给管道体积;Wca,in为电堆阴极入口空气质量流量,等于供气管道出口空气质量流量;Tcp为空压机出口空气温度,

(6)

由于空气供给管道和电堆阴极之间的压力差相对较小,所以采用线性喷嘴方程确定Wca,in,

Wca,in=ksm,out(psm-pca)。

(7)

式中：ksm,out为供气管道出口流量常数;pca为电堆阴极压力,pca=pO2+pN2+psat,其中pO2,pN2和psat分别为阴极氧气、氮气压力和电堆温度下的饱和蒸汽压。

回流管道气体压力变化表达式为

(8)

式中：prm为回流管道压力;Trm为回流管道温度;Vrm为回流管道体积;Wca,out为离开阴极的空气质量流量,Wca,out=kca,out(pca-prm),其中kca,out为阴极出口流量常数;Wrm,out为回流管道出口处空气的质量流量,由于回流管道压力值与外界大气压力值相差较大,故采用非线性喷嘴方程[10]计算其值：

(9)

式中：θ为背压阀门开度;CD为背压阀流量系数;AT为背压阀门最大截面积。

1.3 电堆阴极气体模型

根据质量守恒定律得到电堆阴极内氧气和氮气压力变化的动态方程：

(10)

(11)

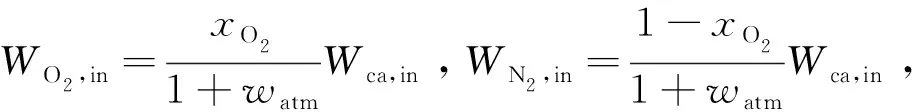
离开阴极的氧气和氮气质量流量由电化学反应后气体中氧气和氮气的质量分数计算得到：

(12)

(13)

式中：Mv为水蒸气的摩尔质量。

对模型做出以下假设：1)所有气体遵循理想气体定律;2)回流管道温度等于电堆温度;3)氢气供给回路得到有效控制,始终使阳极氢气满足负载需求;4)温度和湿度管理系统正常工作,使系统温度和湿度保持在期望值;5)电堆阴极内满足MO2pO2+MN2pN2+Mvpsat=κpca,其中κ=0.025 85[11]。根据文献[7]、文献[11]和文献[12],结合式(1)～式(13)和假设条件,定义状态变量为x=[ωcppsmpcaprm]T,控制输入为u=[u1u2]T=[Vcmθ]T,建立的面向控制的四阶非线性状态空间模型为

(14)

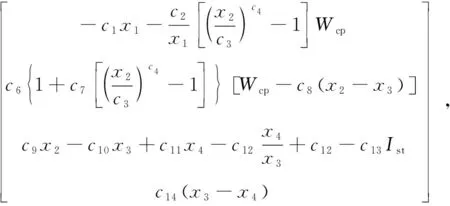
(15)

(16)

(17)

式中：ci(i=1,2,…15)为空气供给系统模型常数,如附录所示。

2 滑模自抗扰控制器设计

燃料电池系统过氧比定义为[13]

(18)

式中：c16和c17为空气供给系统模型常数,如附录所示。系统控制目标为实现对过氧比和阴极压力的解耦控制,而过氧比计算公式中存在干扰电堆电流Ist,对过氧比进行微分会使控制器设计更复杂。所以定义虚拟输出：

(19)

将系统控制输出定义为y=[h1(x)h2(x)]T=[x3x2-x3]T,控制系统框图如图2所示。

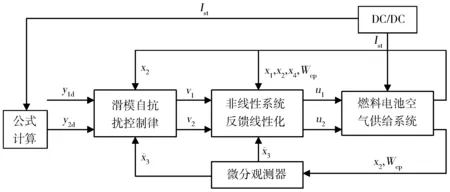
图2 空气供给系统控制框图

2.1 观测器设计

由于电堆阴极内难以安装传感器测量阴极压力x3,所以需要设计观测器估计阴极压力x3的值。对式(15)中空气供给管道压力x2的状态方程进行调整,求出阴极压力x3的表达式：

(20)

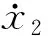
(21)

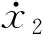
(22)

2.2 反馈线性化控制设计

通过对系统进行反馈线性化,可以将原来耦合的非线性系统解耦成分别控制阴极压力和空气供给管道与阴极之间压力差的两个线性模型,再对两个线性模型分别设计控制器。对系统的两个输出h1(x)和h2(x)求关于g1(x)和g2(x)的一阶与二阶李导数：

(23)

(24)

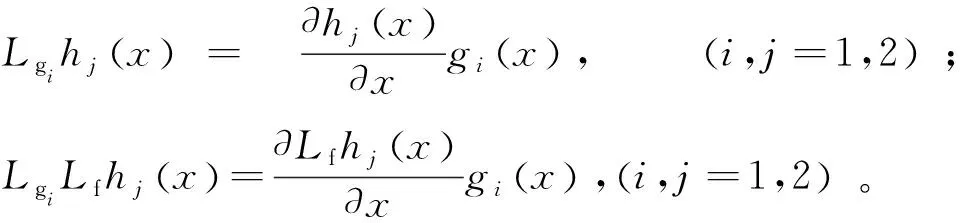
根据相对阶的定义,两个输出的相对阶分别为r1=2,r2=2,空气供给系统的总相对阶为r=4,总相对阶等于系统状态方程的阶数,所以该空气供给系统模型满足精确反馈线性化的要求[15]。

设计新的虚拟输入为v=[v1v2]T,则反馈控制变量为

[u1u2]T=E*(x)-1[[v1v2]T-A*(x)]。

(25)

反馈线性化后的系统为

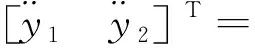
(26)

2.3 自抗扰控制设计

在设计控制器的过程中,需要考虑到实际系统中存在未建模动态和外部未知扰动等系统不确定性,使得建立的面向控制的数学模型与真实的空气供给系统之间存在差异。本研究将系统内部未建模动态视为内部扰动,将内部扰动和外部扰动组成的系统不确定性视为总扰动,设计自抗扰控制律对系统运行时的内外扰动进行实时观测估计并补偿,保证系统对未知扰动的鲁棒性。引入系统不确定性,得到具有扰动项的系统动态模型：

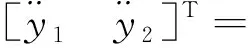
(27)

式中：d1和d2表示扰动,假设幅值有界。

使用跟踪微分器对系统输入信号yid进行处理,设计的二阶跟踪微分器输出信号分别为输入跟踪信号xid1和输入微分信号xid2,具体表达式为[16]

(28)

式中：yid为参考输入信号;xid1为yid的跟踪信号;xid2为xid1的微分信号;fhan(xid1-yid,xid2,ri0,hi0)为最速控制综合函数。

最速控制综合函数[16]公式如下：

(29)

式中：ri0和hi0分别为速度因子和滤波因子,是跟踪微分器的性能整定参数。

改写式(27)并将扰动di扩张成新的状态量,则

(30)

式中：xi3=di为扰动的状态量;bi为扰动的变化率且有界。针对这个系统设计线性扩张状态观测器方程[17]：

(31)

式中：zij(j=1,2,3)为xij(j=1,2,3)的估计值;βij(j=1,2,3)为扩张状态观测器增益。定义观测器误差为δij=xij-zij,(j=1,2,3),则观测器误差动态方程为

(32)

将式(32)写成状态空间表达式：

(33)

扩张状态观测器的增益βij(j=1,2,3)通过带宽配置。式(33)的特征多项式为λ3+βi1λ2+βi2λ+βi3=(λ+ωi0)3,令βi1=3ωi0>0,βi2=3ωi02>0,βi3=ωi03>0,则此时特征多项式为赫尔维茨多项式,其中观测器带宽ωi0>0是观测器唯一的性能整定参数。在bi有界的情况下,观测器具备有界输入有界输出稳定性;当bi=0时,即忽略扰动变化率的情况下,观测器是渐近稳定的。

根据观测效果对扩张状态观测器带宽ωi0进行整定,使观测器能够很好地实时观测状态量xij(j=1,2,3)。

2.4 滑模控制设计

传统的自抗扰控制通过扩张状态观测器获得系统状态量和总扰动的估计值,将跟踪微分器的输出值与扩张状态观测器观测到的估计值做差作为误差量,对误差量进行非线性组合后再补偿总扰动,得到非线性误差反馈控制律[18]。但非线性误差反馈控制律采用的非线性函数调节参数较多且无实际含义,整定过程较为复杂。滑模控制对参数变化及扰动不灵敏,具有很强的鲁棒性,本研究用滑模控制律代替自抗扰控制中的非线性误差反馈控制律,使系统保留了自抗扰控制的抗扰能力的同时具备了滑模控制的快速响应特性[19]。

定义系统误差方程为

(34)

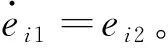
(35)

设计滑模面为

s=ξiei1+ei2,(i=1,2)。

(36)

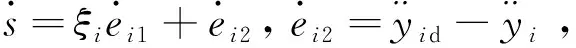
(37)

滑模控制会存在系统抖振问题,采用指数趋近律选取合适的参数能够使运动点远离滑模面时快速趋向滑模面,在运动点接近滑模面时降低趋近速度,使运动点达到滑模面时的速度很小,能够在实现系统快速响应的同时削弱抖振[20]。因此选取指数趋近律为

(38)

式中：εi和ki为需要整定的参数,εi>0,ki>0。结合式(37)和式(38)得出滑模控制律为

(39)

式中,使用扩张状态观测器的观测量zi3替代了扰动di。

(40)

在扩张状态观测器稳定的情况下,观测器能够跟踪系统状态量,di-zi3趋于零,εi和ki为大于零的常数,所以有

(41)

由式(41)可知,系统状态能够在有限时间内达到滑模面,故设计的滑模自抗扰控制器是稳定的。滑模自抗扰控制器整体框图如图3所示。

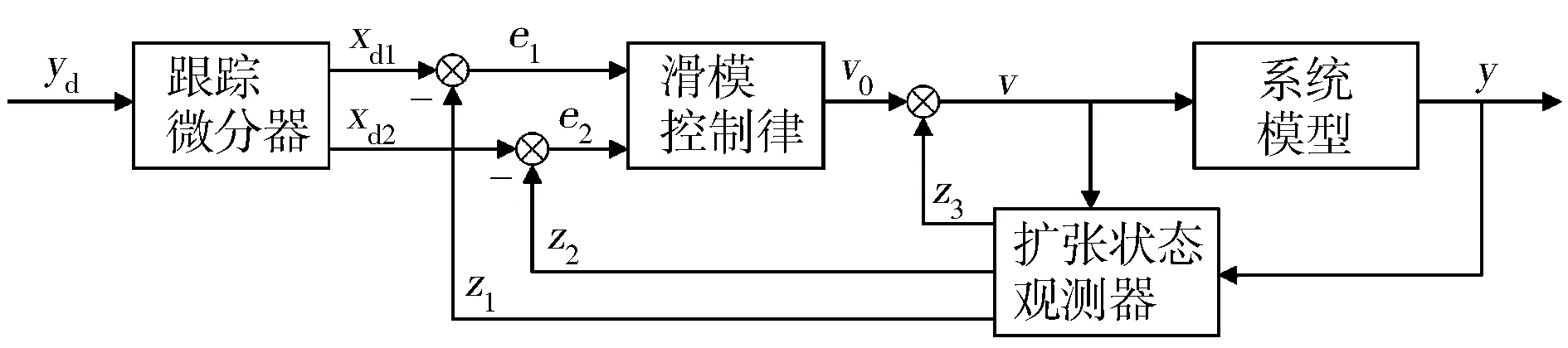
图3 滑模自抗扰控制框图

3 仿真分析

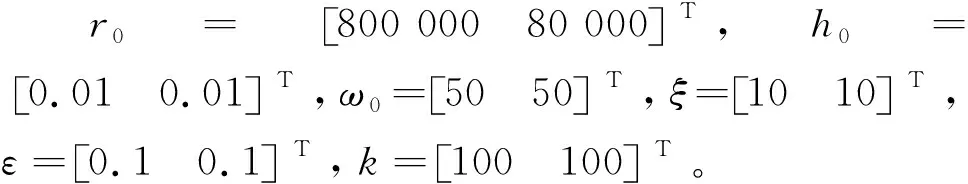
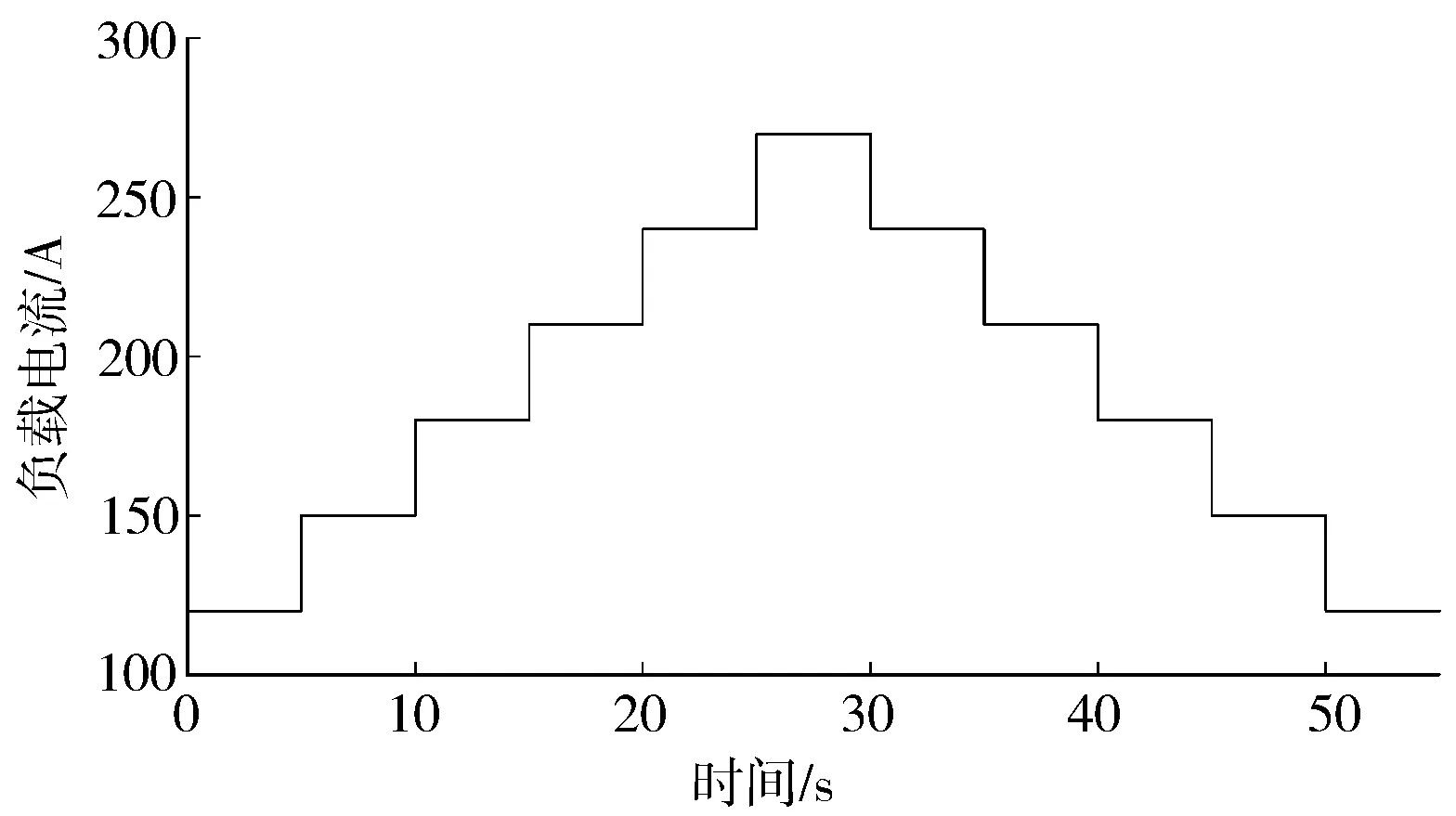
图4 负载电流变化

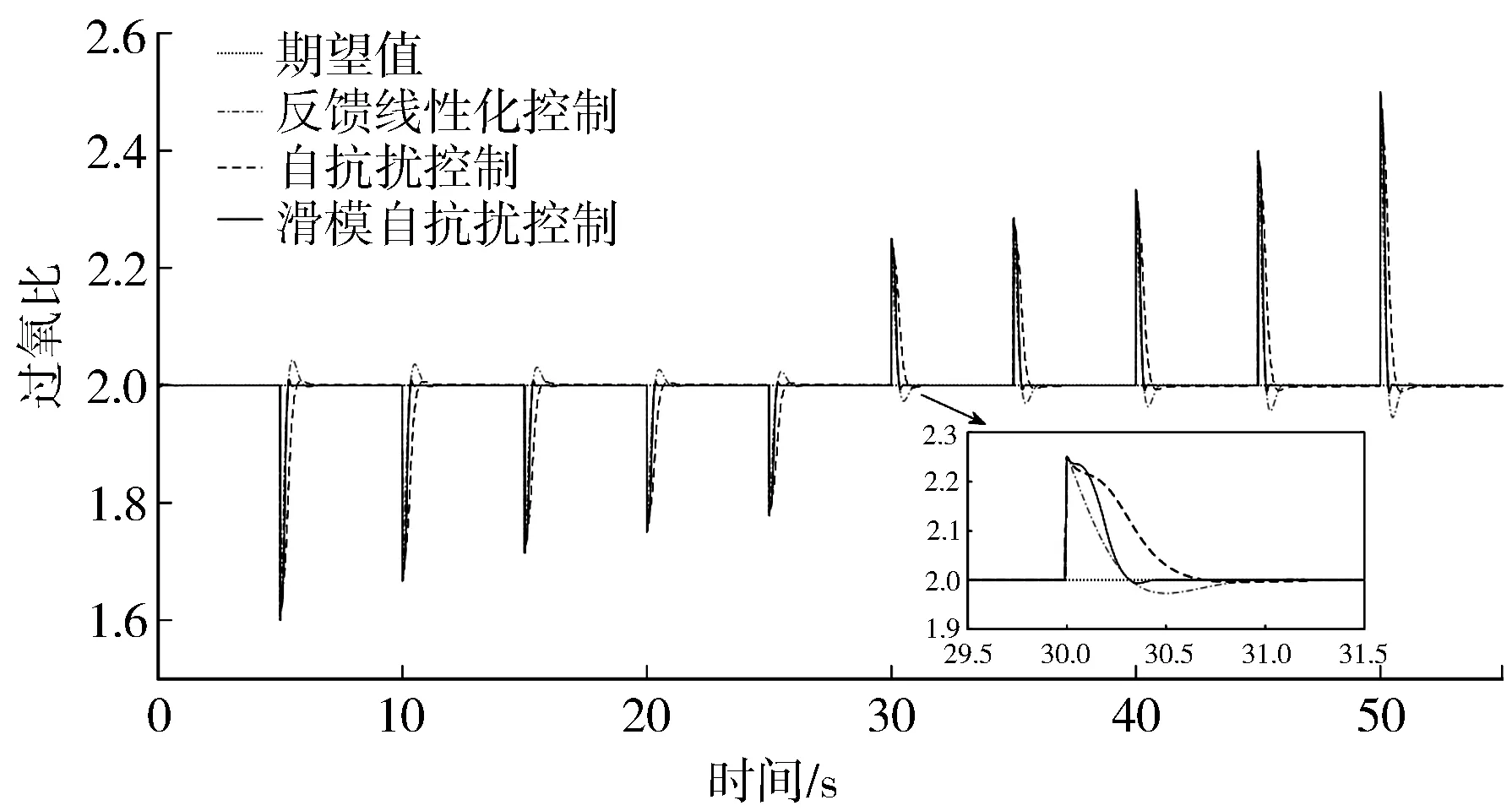
图6 过氧比响应曲线

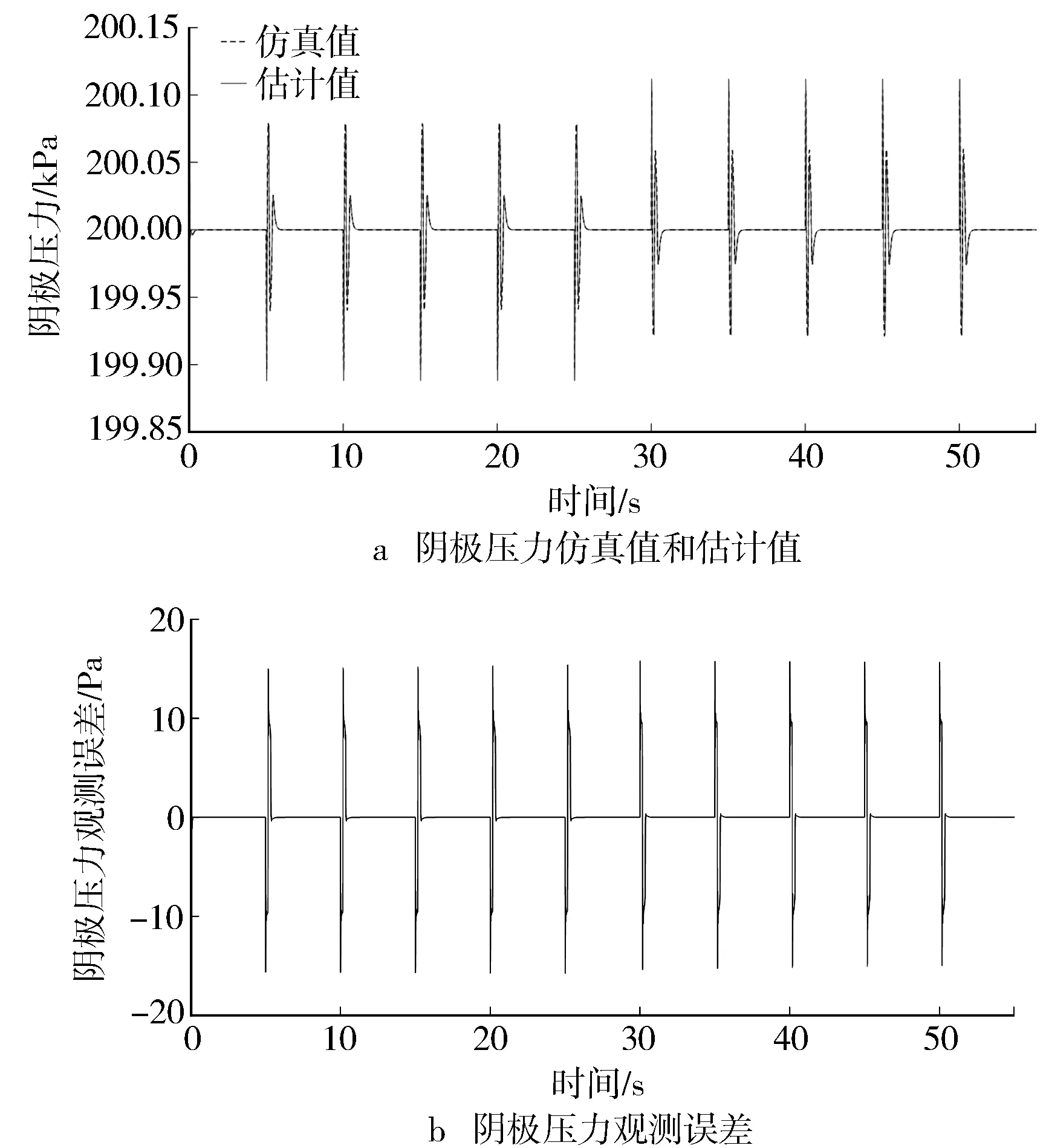
图7 阴极压力和观测误差曲线

考虑到燃料电池运行过程中会存在对测量信号的噪声污染,给定与图4相同的负载电流变化,分别对空压机转动角速度测量信号、供给管道压力测量信号和回流管道压力测量信号叠加方差为0.01的高斯白噪声,采用与上文相同的三种控制策略对空气供给系统进行控制,系统的阴极压力响应曲线和过氧比响应曲线如图8和图9所示。

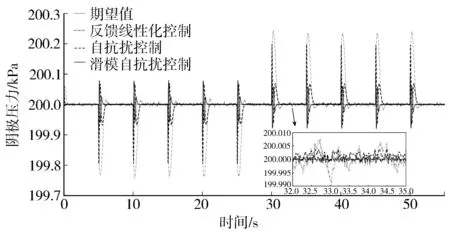
图8 引入测量噪声后的阴极压力响应曲线

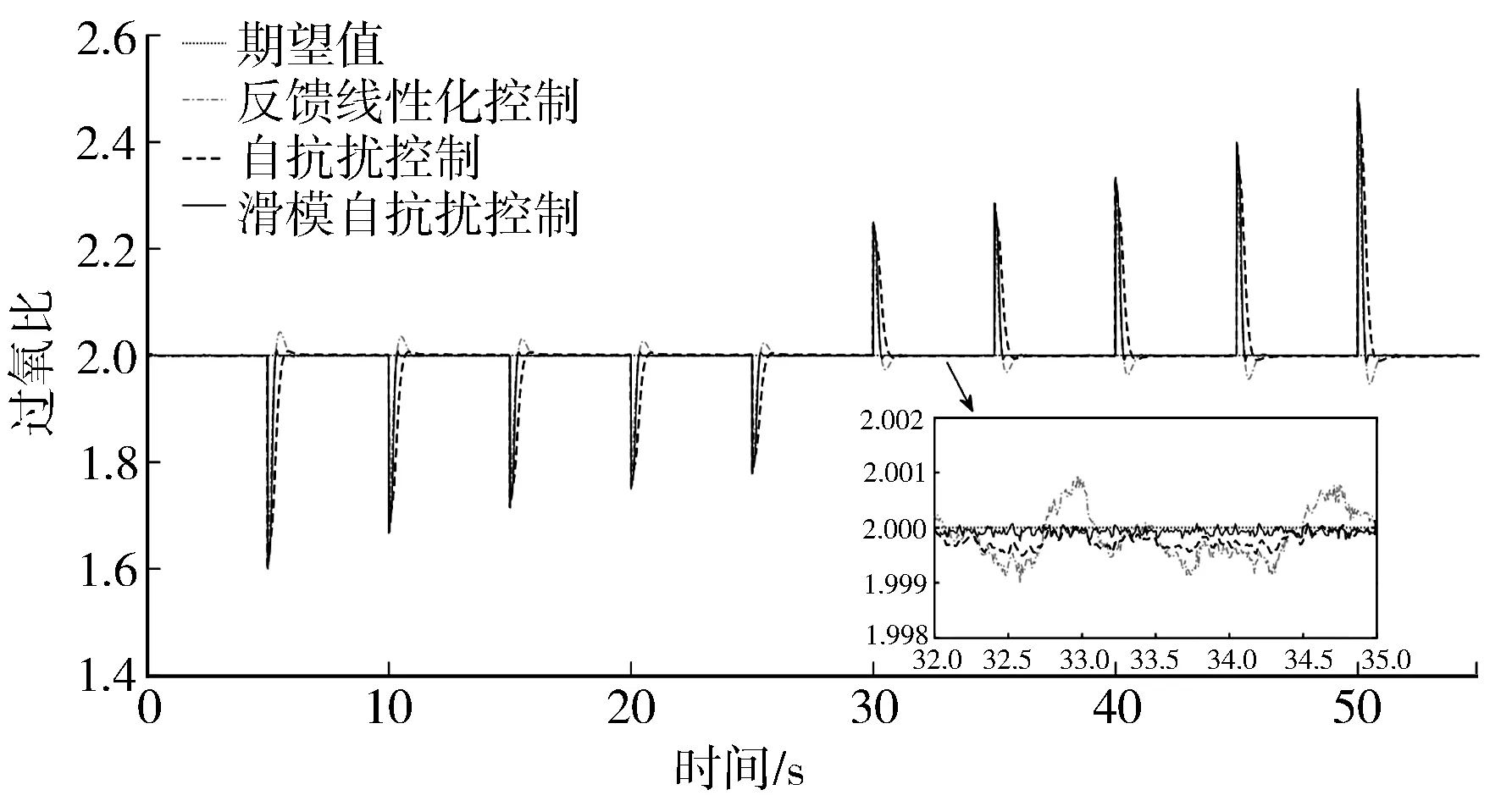
图9 引入测量噪声后的过氧比响应曲线

由图可知,三种控制策略都能控制阴极压力和过氧比收敛于期望值附近,但是滑模自抗扰控制的稳态误差比状态反馈控制和自抗扰控制小,验证了设计的滑模自抗扰控制器的鲁棒性。

仿真结果表明,本研究设计的控制策略在负载电流变化的条件下能够使系统实现对阴极压力和过氧比期望值的准确跟踪,而且调节速度较快,抗干扰能力较强。这是因为当负载电流发生变化时,系统状态变量偏离期望值,系统误差变大,引入的滑模控制律能够快速改变控制量,使系统动态响应迅速,而且控制量中实时补偿了扩张状态观测器估计的系统扰动值,保证了控制器对扰动的鲁棒性。

4 结束语

针对质子交换膜燃料电池空气供给系统进行研究,建立了面向电堆阴极压力和过氧比控制的空气供给系统四阶非线性状态空间模型。本研究设计的基于反馈线性化的滑模自抗扰控制策略在负载电流变化的情况下能够使系统准确跟踪阴极压力和过氧比期望值,相比于状态反馈控制和传统自抗扰控制,阴极压力调节时间分别缩短约45%和30%,阴极压力超调量分别减小约56%和47%,过氧比调节时间分别缩短约69%和67%。在负载电流变化和存在测量信号噪声污染的情况下,系统的稳态误差小于状态反馈控制和传统自抗扰控制,验证了提出的控制算法的鲁棒性。