小水电机组的变转速运行方案及控制策略研究

2023-08-28文贤馗沈春和古庭赟熊军超

中国农村水利水电 2023年8期

苏立，文贤馗，毛成，沈春和，古庭赟，牛唯，熊军超

（贵州电网有限责任公司电力科学研究院，贵州贵阳 550002）

0 引言

我国水电资源储量丰沛，发电站装机容量在50 MW 及以下的被称为小水电，我国小水电电站约有4.5 万座，占全国总发电量的约5%，是农村电力的重要来源之一［1］。因地制宜地开发小水电资源对拦洪蓄水、改善能源结构、促进生态环境保护及山区贫困地区的脱贫致富等具有重要作用，对促进我国农村、经济、环境协调发展具有十分重要的意义［2-5］。

小水电受水位变化大、来水量不定等因素影响［6］，目前常规的固定转速水力发电机组普遍存在运行效率低、调节品质差等问题，限制了小水电的健康发展［7］。章枫等人［7］指出峰谷时段对小水电发电产生了一定影响；彭文启等人［8］分析了小水电的河流生态流量的重要性，该流量要求必然对机组发电量造成一定的影响和约束；陈志峰等人［9］以韶关地区为例分析了小水电机组并网与离网模式切换时对电网频率的影响。

近年来，变速水力发电机组因其宽工况调节效率高、机组调节性能良好等优点受到行业青睐［10］，在机组水头、来流等参数大范围变化造成机组偏离高效率运行区时，通过调整机组转速使水轮机运行工况重新返回高效率运行区，从而可以提高机组运行效率、改善机组运行工况［11，12］。同时，采用合理的控制方式还可以在瞬态过程中通过快速改变机组转速实现机组转动动能的快速释放或储存，极大加快了机组功率的响应速度，对稳定电网频率、避免水电机组功率反调、改善机组调节品质等方面均具有明显优势［13，14］。目前针对水电机组变速运行的研究主要针对容量较大的机组或抽水蓄能机组［15，16］，对小水电机组采用变速运行的研究较少，对于适宜小水电机组的变速运行方案及控制策略尚不清楚。

1 变速运行方案及系统数学模型

工程中实现水力发电机组连续变速运行的方案主要有两种，即如图1 所示的基于部分功率变流器与双馈电机的变速水力发电系统方案以及如图2所示的基于全功率变流器与同步发电机的变速水力发电系统方案［17］。

图1 基于部分功率变流器与双馈电机的变速方案Fig.1 Variable speed hydroelectric generating unit based on part power converter

图2 基于全功率变流器与同步发电机的变速方案Fig.2 Variable speed hydroelectric generating unit based on full power converter

在图1 的方案中采用了双馈异步发电机，其转子绕组通过变流器与电网连接，变流器容量需大于转子绕组流过的功率，一般约为电机额定容量的30%，具有变流器容量小的优点，但存在电机结构复杂，机组转速变化范围小等缺点；在图2的方案中采用了永磁同步发电机，电机定子通过变流器与电网相连，变流器容量需大于电机容量，电机容量相对较大，但电机结构简单，且机组转速变化范围较大。

小水电机组的运行工况变化范围一般较大，所需要的机组转速变化范围较大，同时机组结构应尽可能简单且易维护。因此，如图2 所示的基于全功率变流器与同步发电机的变速方案更适宜于小水电机组采用。

1.1 引水管道数学模型

在系统瞬态过程中引水管道的水击现象造成机组水头、流量等参数的瞬时变化，常采用水击基本方程描述其瞬变过程［18］，采用特征线法求解该水击数学模型，以获得更为精细的管道水击过渡过程。其数学表达式为：

式中：Q为管道内流量；H为管道内能头；L为沿管道中心线方向的长度；A为管道横截面积；a为水击波速；θ为管道倾放角；g为当地重力加速度；λ为管道沿程损失系数；d为管道横截面积。

1.2 水轮机数学模型

认为水轮机动态过程中各时刻运行工况与对应的稳定工况特性一致，同时忽略水轮机的比尺效应，即可以采用水轮机模型综合特性数据表征真机的动态过程［18］，其数学模型为：

式中：Q11为水轮机单位流量；n11为水轮机单位转速；M11为水轮机单位力矩；y为水轮机导叶开度；fq为水轮机模型流量特性关系；fm为水轮机模型力矩特性关系。

由水轮机相似性，单位参数与原型参数之间满足：

式中：n为水轮机转速；D1为水轮机标称直径；Ht为水轮机工作水头；Qt为水轮机流量；Mt为水轮机力矩。

采用实测的水轮机模型综合特性曲线数据作为式（2）的输入与输出表达式，以充分表达出水轮机动态过程中的非线性特征。

1.3 永磁同步发电机数学模型

永磁同步发电机在旋转两相坐标下的数学模型可以表示为［19］：

式中：usd为d 轴定子电压；usq为q 轴定子电压；Rs为定子绕组电阻；isd为d 轴定子电流；isq为q 轴定子电流；ωs为电机同步角速度；Lsd为d轴电感；Lsq为q轴电感；ψf为永磁体磁链。

电机的扭矩方程可以表示为：

式中：Me为发电机力矩；np为发电机磁极对数。

1.4 变流器数学模型

机侧变流器的数学模型表示为：

式中：esd为发电机的d 轴感应电动势；esq为发电机的q 轴感应电动势；Ssd为机侧变流器开关函数的d 轴分量；Ssq为机侧变流器开关函数的q轴分量；Udc为直流母线电压；C为直流母线电容；iL为直流母线流至网侧变流器的电流。

网侧变流器的数学模型表示为：

式中：ugd为网侧变流器的出口d 轴电压；ugq为网侧变流器的出口q轴电压；egd为电网d轴电压；egq为电网q轴电压；Rg为网侧滤波电阻；igd为网侧d轴电流；igq为网侧q轴电流；Lgd为网侧d轴滤波电感；Lgq为网侧q 轴滤波电感；ωg为网侧同步角速度；Sgd为网侧变流器开关函数的d 轴分量；Sgq为网侧变流器开关函数的q轴分量；idc为机侧变流器流至直流母线的电流。

1.5 导叶随动系统数学模型

考虑水轮机导叶位置约束及运动速度约束的水轮机导叶随动系统数学模型，其结构框图如图3所示。

图3 水轮机导叶随动系统框图Fig.3 Hydraulic turbine servo system block diagram

表示为：

式中：y为导叶开度；ymax为导叶开度最大限制值；ymin为导叶开度最小限制值；Ty为接力器响应时间常数；v为主配压阀行程；s为拉普拉斯算子。

其中的主配压阀行程表示为：

式中：vmax为主配压阀行程最大限制值；vmin为主配压阀行程最小限制值；yg为调速器的调节器输出值；Tyb为主配压阀响应时间常数。

2 控制策略分析

2.1 控制策略1

通过调速器控制水轮机导叶开度实现机组功率稳定、通过机侧变流器控制水轮机转速稳定、通过网侧变流器控制变流器直流母线电压及无功功率稳定的控制策略。其中调速器的控制策略框图如图4 所示。与机组定转速不同，变速运行时机组转速与电网频率解耦，在该变速方案中采用变流器控制机组转速稳定，因此采用调速器仅对机组有功功率进行控制。

图4 策略1的水轮机调速器控制框图Fig.4 The control block diagram of hydraulic turbine governor on strategy 1

调速器的调节器输出值表示为：

式中：KP为调速器的比例增益；KI为调速器的积分增益；KD为调速器的微分增益；TD为微分项时间常数；Pr为机组功率给定值；P为机组功率测量值。

机侧变流器用于控制水轮机转速稳定，采用双闭环矢量控制的控制策略框图如图5所示，其中内控制环为电流环，外控制环为转速环，为降低永磁体的去磁现象，将d轴电流环的电流给定设置为0。

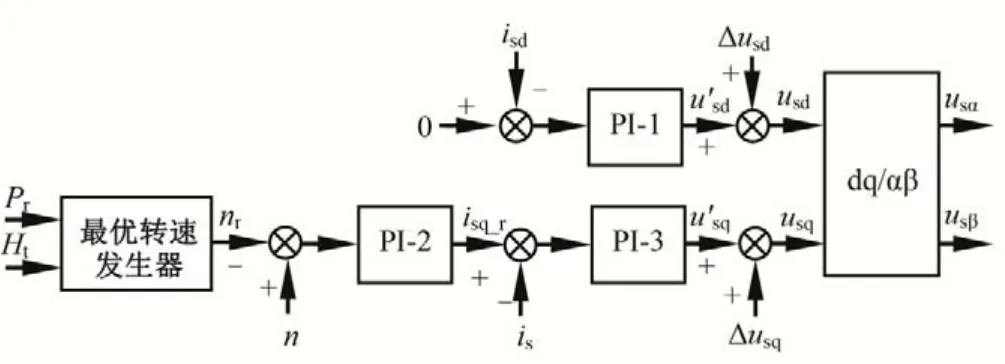
图5 策略1的机侧变流器控制框图Fig.5 The control block diagram of machina side converters on strategy 1

最优转速发生器为根据水轮机模型综合特性曲线所得的最优转速与机组水头H、功率给定Pr之间的关系，表示为：

式中：fn为水轮机最优转速关系；Ht为水轮机工作水头；nr为水轮机最优转速。

电流内环可以表示为：

式中：KP1为机侧d 轴电流内环比例增益；KI1为机侧d 轴电流内环积分增益；KP3为机侧q 轴电流内环比例增益；KI3为机侧q 轴电流内环积分增益；isq_r为机侧q 轴电流给定；Δusd为机侧d 轴解耦补偿项；Δusq为机侧q轴解耦补偿项。

机侧解耦补偿项的表达式为：

由转速外环得到的q轴电流给定值表示为：

式中：n为机组转速测量值；KP2为机侧q 轴转速外环比例增益；KI2为机侧q轴转速外环积分增益。

网侧变流器用于控制直流母线电压及输出至电网的无功功率，采用双闭环矢量控制的控制策略框图如图6所示，其中内环为网侧变流器电流控制环，d轴外环为直流母线电压控制环，q轴电流给定值为输出值电网的无功电流大小。

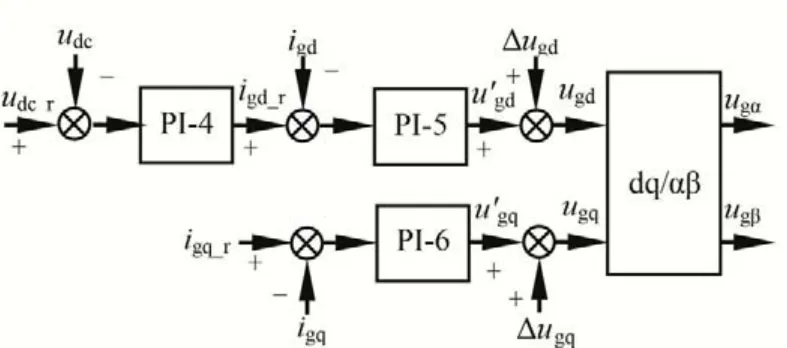
图6 网侧变流器控制框图Fig.6 The control block diagram of grid side converters

电流内环的可以表示为：

式中：KP5为网侧d 轴电流内环比例增益；KI5为网侧d 轴电流内环积分增益；KP6为网侧q 轴电流内环比例增益；KI6为网侧q 轴电流内环积分增益；igd_r为网侧d 轴电流给定；igq_r为网侧q 轴电流给定；Δugd为网侧d 轴解耦补偿项；Δugq为网侧q 轴解耦补偿项。

机侧解耦补偿项的表达式为：

由电压外环得到的d轴电流给定值表示为：

式中：udc_r为变流器直流母线电压给定值；udc为变流器直流母线电压测量值；KP4为网侧d 轴转速外环比例增益；KI4为网侧d 轴转速外环积分增益。

2.2 控制策略2

通过调速器控制水轮机导叶开度实现机组转速稳定、通过机侧变流器控制水轮机有功功率稳定、通过网侧变流器控制变流器直流母线电压及无功功率稳定的控制策略。其中调速器的控制策略框图如图7所示。

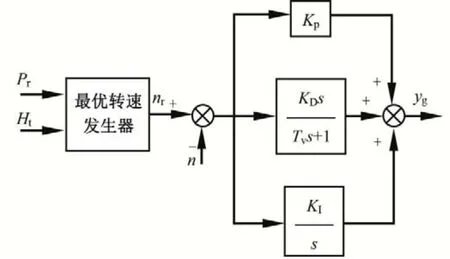
图7 策略2的水轮机调速器控制策略框图Fig.7 The control block diagram of hydraulic turbine governor on strategy 2

调速器的调节器输出值表示为：

机侧变流器用于控制水轮机有功功率稳定，采用双闭环矢量控制的控制策略框图如图8所示，其中内控制环为电流环，外控制环为有功功率控制环，为降低永磁体的去磁现象，将d轴电流环的电流给定设置为0。

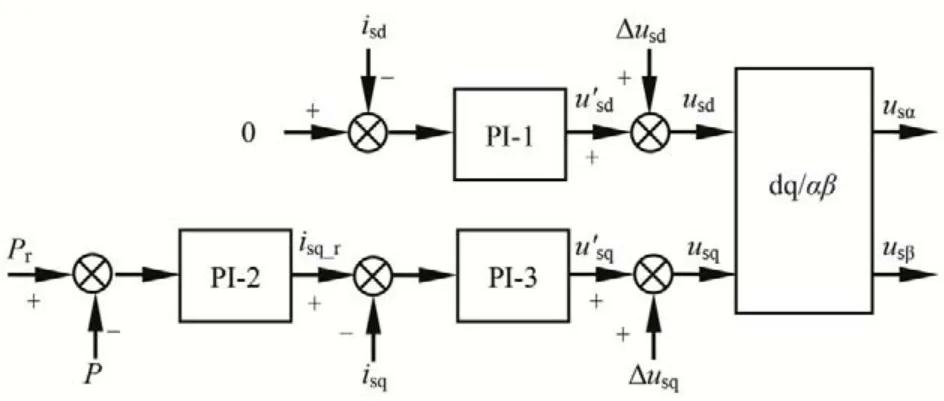
图8 策略2的机侧变流器控制策略框图Fig.8 The control block diagram of machina side converters on strategy 2

电流内环的控制与控制策略1 相同，可以采用式（12）进行表示。有功功率外环可以表示为：

网侧变流器用于控制直流母线电压及输出至电网的无功功率稳定，其控制与控制策略1的网侧变流器控制相同，其控制框图如图6所示。

2.3 定转速控制策略

传统的定转速机组接线方式中采用同步发电机，电机定子绕组直接与电网进行连接，采用调速器控制机组转速及功率，调速器的控制策略框图如图9所示。

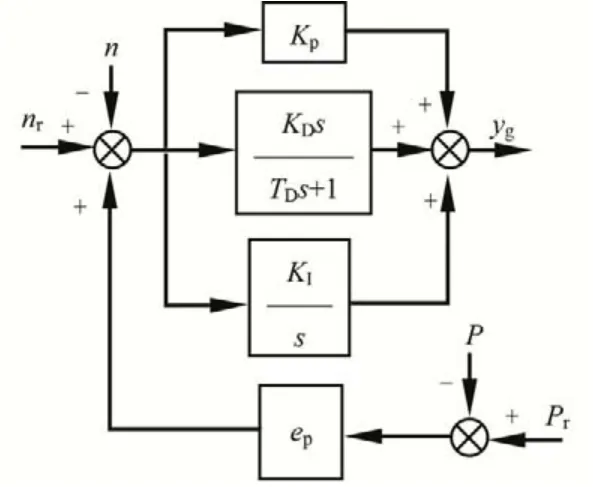
图9 定转速机组的水轮机调速器控制策略框图Fig.9 The control block diagram of fix speed hydraulic turbine governor

此时调速器的输出可以表示为：

式中：ep为调速器的调差率。

2.4 控制效果分析

以某典型水电站为例进行分析，该电站的引水管道长L=6.5 m，管道直径d=3 m，水击波速a=1 000 m/s，重力加速度g=9.8 m/s2，机组容量为700 kW，水轮机直径D1=2.5 m，水轮机额定水头为3 m，水轮机同步转速nr=125 r/min，机组机械惯性时间常数Ta=7.5 s，定子绕组电阻Rs=0.011 7 Ω，定子绕组电感d轴分量Lsd=0.000 71 H，定子绕组电感q 轴分量Lsq=0.000 71 H，直流母线电容容量C=0.06 F，永磁体磁链ψf=1.35 T，电机磁极对数np=24，滤波电阻Rg=0.001 3 Ω，滤波电感的d 轴分量Lgd=0.000 415 H，滤波电感的q轴分量Lgq=0.000 415 H，机组并入无穷大电网，电网电压的d 轴分量egd=332 V，电网电压的q 轴分量egq=0 V，感应电动势的d轴分量esd=0 V，感应电动势的q轴分量esq=6.3 kV，调速器的调差率ep设置为0.04。

机组初始工况为额定工况，分别在控制策略1、控制策略2以及定速控制策略下功率给定降低20%，所得动态过程如图10所示，对应的主要指标如表1所示。由于机组并入无穷大电网，动态过程中电网频率、电压等参数维持不变，不再展示电网相关参数的曲线。

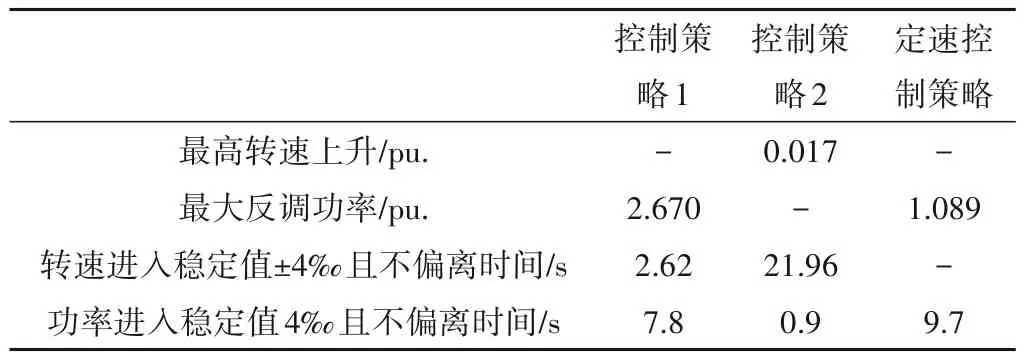
表1 不同控制策略的动态指标Tab.1 Dynamic indexes of different control strategies

图10 不同控制策略的动态过程Fig.10 Dynamic process of different control strategies

由仿真结果可以看出，采用传统的定转速运行策略时，机组转速与电网频率对应，由于针对小水电机组，可认为机组并入无穷大电网，在过渡过程中机组转速不发生变化，但在调节过程中由于导叶动作机组功率发生了反调现象，其反调功率最大可达1.089 pu.，功率进入稳定值4‰且不再偏离的时间为9.7 s。

控制策略1 具有较快的转速调节速度，且转速波动范围较小，调节过程中转速无反方向波动过程，但功率调整速度较慢，且出现了极大的功率反调，最大功率可达2.67 pu.，造成这一现象的原因是机组功率降低时最优转速下降，快速的转速下降释放了部分机组转动能量，同时导叶关闭造成了短时间内的水轮机反调功率，这两部分功率在短时间内产生叠加后造成发电机功率的快速增加形成极大的功率反调现象，这无疑对发电机提出了更大的挑战。

控制策略2 具有较快的功率调节速度，仅在0.9 s 即可使机组功率进入稳定值的4‰内且不再偏离，同时功率调节过程无反调现象，但机组转速调节速度较慢，且调节过程中出现短时的转速反向波动。这是由于发电机输出功率快速降低，造成能量以机械能的方式在机组转速上累积，同时水轮机导叶关闭造成的反调增加了机械能的累积速度，但水轮机一般具有相对较大的飞轮力矩与良好的飞轮储能能力，转速上升仅为1.7%，伴随着机组功率稳定后的导叶继续调节机组转速再逐步稳定至新的稳定值。

由上述的三种控制策略的对比可以看出，采用控制策略1与控制策略2 均可实现机组稳定运行工况点的转速调整，即均满足机组变速运行的稳定工况要求，控制策略2 同时还可以加快机组功率调节速度、消除功率反调现象、对发电机无特殊的附加要求，因此更加适宜于小水电机组的变速运行。