基于GSA-GPC 水电机组预测控制

王莺子，谌慧铭，陈金保，曾 荃，陈 上，肖志怀

（1. 国网湖北省电力有限公司技术培训中心，湖北 武汉 430072； 2. 武汉大学动力与机械学院，湖北 武汉 430072；3. 中国长江电力股份有限公司三峡电厂，湖北 宜昌 443000）

0 引 言

近年来，清洁能源开发和输电网络建设在我国得到大力推进。水电、风电、光伏等在电网中的大比例增加，导致电网结构发生重大变化，逐步形成以清洁能源为主体的新型电力系统网络结构。在新型电力系统中，水电机组不再仅担任传统的调峰调频、事故备用等角色，将更多处于变工况运行状态，运行环境相比过去更加恶劣［1，2］。因此，水电机组变工况运行控制技术亟需提高。

水轮机调节系统是一个具有复杂非线性且时变的系统，常用的是结构简单、参数易调整的PID控制器［3-5］。为提高控制品质，一些学者开展了PID 参数优化、先进控制策略等方面的研究。在PID 参数优化方面：Chen 提出了一种自适应网格粒子群优化算法来解决水轮机调节系统的PID增益调整问题［6］；Magdy提出了基于粒子群优化的最优PID 控制器，并将其应用于埃及电力系统，以实现基于分散数字模型的负荷频率控制［7］；Chen将混沌非支配排序遗传算法II（NSGAII）应用于优化分数阶PID控制器，并通过仿真和一些实验结果验证了分数阶控制器相对于整数控制器的优越性［8］。在先进控制策略方面：Chen 将改进的模糊人工蜂群算法与改进的PID-SMC 控制器相结合，以改善非线性水轮机调节系统的动态性能［9］。Chen 将混合帝国主义竞争算法（HICA）和模糊滑模控制器（FSMC）相结合，以减少FSMC 的抖振［10］。Zhou 提出了一种基于Takagi-Sugeno 模糊模型的自适应广义预测控制器，以提高控制性能并抑制抽水蓄能机组的“S”特征区域不稳定性［11］。Xiao 提出了一种一步超前预测控制器，通过结合一步超前神经预测器和一个神经控制器来生成最优控制信号［12］。

在工程实际中，通常设置一组PID 参数，以应对PID 控制器对于工况的敏感性。但由于参数数量有限，PID 控制器仅能满足部分工况的调节品质。为此，具备自适应调节能力的在线训练控制器具备更好的应用前景。作为在线训练控制器的代表之一，广义预测控制（Generalized Predictive Control，GPC）具备优良的控制性能和鲁棒性，在石油、化工、冶金、机械等领域得到有广泛应用［13-15］。GPC 也称为模型预测控制，与其它传统控制方法相比，广义预测控制对于模型的功能而不是结构与形式更加注重，能通过已知数据信息预测系统未来的输出行为。不注重模型结构形式而更加注重基于系统输入输出的动态特性建立预测模型是GPC 优于其它控制算法的原因之一，也是其能在工程实践中广泛应用的前提。

基于GPC 优良的自适应特性，本文将其引入大型水轮机调节系统控制器设计，并采用引力搜索算法（GSA）对GPC 参数进行优化，实现了基于GSA-GPC 的水电机组最优控制。同时，基于实际电站数据搭建水轮机调节系统仿真平台，通过仿真对比试验验证了GSA-GPC优异的控制效果、巨大的应用潜力。

1 水轮机调节系统数学模型

1.1 水轮机模型

水轮机是参数可变、饱含非线性的原动机，通常可以建立非线性模型或线性模型，如式（1）和（2）所示。在对模型精度要求高时，一般采用基于特性曲线的非线性水轮机模型，可利用插值、神经网络等方式构建［14-16］。为确保模型精度，本文采用原型水轮机试验数据，基于BP 神经网络构建水轮机模型，然后在指定工况下将其线性化得到对应的传递系数。

式中：Q为水轮机流量；Mt为水轮机力矩；X为机组转速；Y为导叶开度；H为工作水头；eqx、eqy和eqh分别为Q对X、Y和H的传递系数；ex、ey和eh分别为Mt对X、Y和H的传递系数；q、mt、x、y和h分别表示Q、Mt、X、Y和H的偏差相对值。

1.2 引水系统模型

引水系统由上下游水库、引水管道、电站内水轮机流道、尾水管等部位构成。对于压力管道较短的水电站，采用刚性水击模型即可满足计算精度要求，对于水头较高或者压力管道长度超过600～800 m的水电站则需要考虑水流和管道弹性造成的影响，应采用简化弹性水击模型来描述管道中的流体运动。考虑本文研究的机组压力管道长度较短，因此采用如式（3）所示的刚性水击模型［15］。

式中：Tw为水流惯性时间常数。

1.3 调速器模型

水轮机调速器包含控制器和电液随动系统两个部分，目前国内外水电站普遍选用PID 调节控制规律的控制器。PID 控制器包含串联PID 和并联PID 两种基本结构［3，4］。本文研究的实际电站采用的是并联PID型控制器，如式（4）所示。

式中：KP、KI和KD分别为控制器的比例、微分和积分系数；T1v为微分环节时间常数。

电液随动系统主要由中间接力器、主接力器、电液转换器、配压阀等元器件组成，且存在死区、限速、延迟等非线性环节。若忽略非线性环节作用，则对应的传递函数如式（5）所示。

式中：Ty与Ty1分别为主接力器和中间接力器的反应时间常数。

1.4 发电机模型

对于水轮机调节系统动态特性研究，由于发电机中的电磁暂态响应通常比水轮机的水力机械响应快，通常不考虑机组电气瞬变过程，即忽略发电机转子和励磁调节器的电磁暂态［2，3］。因此，发电机及负载特性采用一阶惯性环节描述，如式（6）所示。

式中：Ta为机组惯性时间常数；eg为发电机负载自调节系数；Mg0为负载力矩。

1.4 水轮机调节系统整体模型

联合控制器、随动系统、发电机、水轮机及引水系统等各子系统的数学模型，即得到功率模型下水轮机调节系统的分段线性化模型，如图1 所示。其中，由于接入无穷大电网，不考虑转速变化，即反馈频率等于频率给定值（fe=fc）；机组有功功率相对变化pt近似等于水轮机力矩相对变化（pt=mt），即考虑水轮机力矩反馈；pc为机组有功功率给定值。需要注意的是，图1 中传递系数是随工况变化的，即需要根据指定工况对非线性水轮机模型输出求偏导以得到对应传递系数。

图1 水轮机调节系统的分段线性化模型Fig.1 Piecewise linearization model of hydraulic turbine governing system

2 基于GSA的广义预测控制

GPC优异的控制性能源于3个基本要素：预测模型、滚动优化和反馈校正［13］。为进一步提高其控制品质，本文采用GSA 算法对其超参数进行优化。

2.1 预测模型

GPC 预测功能的实现是基于预测模型，可选的预测模型有传递函数、状态方程、脉冲响应、阶跃响应、易于在线辨识的带控制量的自回归积分滑动平均模型（CARIMA）等［14］。其中，CARIMA可用来描述不稳定系统在内的任意对象。考虑水轮机运行工况复杂，本文预测模型选用CARIMA［15］，如式（7）所示。

式中：A（z-1）、B（z-1）、C（z-1）分别是n、m和n阶z-1的多项式；Δ=1-z-1为差分算子。y（k）、u（k）、ξ（k）分别为系统的输出信号、输入信号和白噪声。

2.2 滚动优化

假定系统时延d=1，则式（7）可表示为式（8）。若系统延时d＞ 1，只需令多项式B（z-1）中前d-1项系数为零即可，即b0=b1=b2…=bd-2= 0［15］。

等式两边同时乘以差分算子将预测模型简化为：

基于预测模型式（8）得到使预测误差的方差最小的最优预测误差：

式中：Ej（z-1）为Diophantine方程的解。

证明过程如下：

将（k+j）时刻的输出预测误差记为式（11）：构造Diophantine方程：

式中，多项式E（z-1）、F（z-1）、G（z-1）的表达式为：

将式（12）第一个式子代入式（9）并且等式两边同时除以多项式A，得：

将式（9）移项，两边同时除以多项式C得：

将式（15）代入式（14），联立式（13）第二个式子，并化简得：

将式（16）代入使预测误差的方差最小的性能指标并展开得：

式（17）等式右边第一项不可控，第二项为0（E（ξ） = 0）。欲使J最小，则需使上式第三项为0，即式（18）成立。

此时性能指标为最小值如式（19），且此时的最优预测误差为式（10），证明完毕。

对于GPC 滚动优化，通过在线求解多步Diophantine 方程，得出E、F、G三个多项式后即算出控制量［13］。

Diophantine 方程的初值如式（20），Ej（z-1）、Gj（z-1）和Fj（z-1）系数迭代公式如式（21）-（23）［14］。

2.3 反馈校正

由于选用的CARIMA 只是对系统动态特性进行粗略估计，因此为使得CARIMA 与复杂的时变非线性水轮机调节系统相匹配，需要对其进行实时反馈校正才能得到优异的控制效果。本文选用带遗忘因子的递推最小二乘法来对预测模型进行反馈校正［13］。由式（8）得预测模型当前的输出：

式中，na和nb为多项式A和B的阶数；φ（k）和θ满足：

采用的递推最小二乘法迭代公式［14］：

式中，λ为遗忘因子，取值通常为［0.9，1］。

最小二乘法递推公式循环流程如下：

Step 2：采样当前输出信号y（k）和输入信号u（k）。

Step 3：利用式（25）计算K（k）、(k)和P（k）。

Step 4：循环数k+1，返回Step2，继续循环。

2.4 GPC算法流程

本文仅考虑白噪声形式的不确定性扰动，故CARIMA 模型中取C（z-1） = 1。当C（z-1） = 1时，预测模型式（16）可简化为：

式（26）对应矩阵形式为：

式中：N为预测长度；Y1=F2ΔU（k-j） +GY（k）为基于过去输入输出的输出预测响应；Y= ［y（k+ 1），y（k+ 2），…，y（k+N）］T为未来的预测输出；ΔU= ［Δu（k），Δu（k+ 1），…，Δu（k+N- 1）］T为当前和未来的控制增量向量；ΔU（k-j）= ［Δu（k- 1），Δu（k-2），…，Δu（k-nb）］T为过去的控制增量向量；Y（k） = ［y（k），y（k- 1），…，y（k-na）］T为当前及过去的实际输出；ξ= ［ξ（k+ 1），ξ（k+ 2），…，ξ（k+N）］T为未来的白噪声向量。

综合考虑使控制量最小且输出在给定范围内，选取性能指标：

式中：N1为最小输出长度，一般取N1=d；N2为输出长度，一般取N2=N；Nu为控制长度，Nu≤N2。

式（28）对应矩阵形式为：

式中：Yr=［yr（k+N1），yr（k+N1+1），…，yr（k+N）］T，为未来的参考轨迹输出。为确保输出平稳性，一般取yr（k+j）=αyr（k+j-1）+（1-α）w（j=1， 2， …，N）。其中，α∈［0，1］，为输出柔化系数；w为输出设定值。

为使性能指标取最小值，需∂J/∂ΔU= 0，求得广义预测控制的控制向量：

当前时刻的控制量为：

2.5 基于GSA的GPC参数优化

为获得全局最优控制效果，采用GSA［18］对GPC 性能主要影响参数（N、Nu和α）进行优化。该优化分别在最小水头、额定水头和最高水头下选取Y=40%和80%组成6 个典型工况，即适应度函数考虑6个工况。采用的适应度函数为：

式中：t为实际时间；ts为仿真总时间；ec(t)为第c个工况下机组有功功率控制偏差。

GSA优化GPC超参数流程见图2。

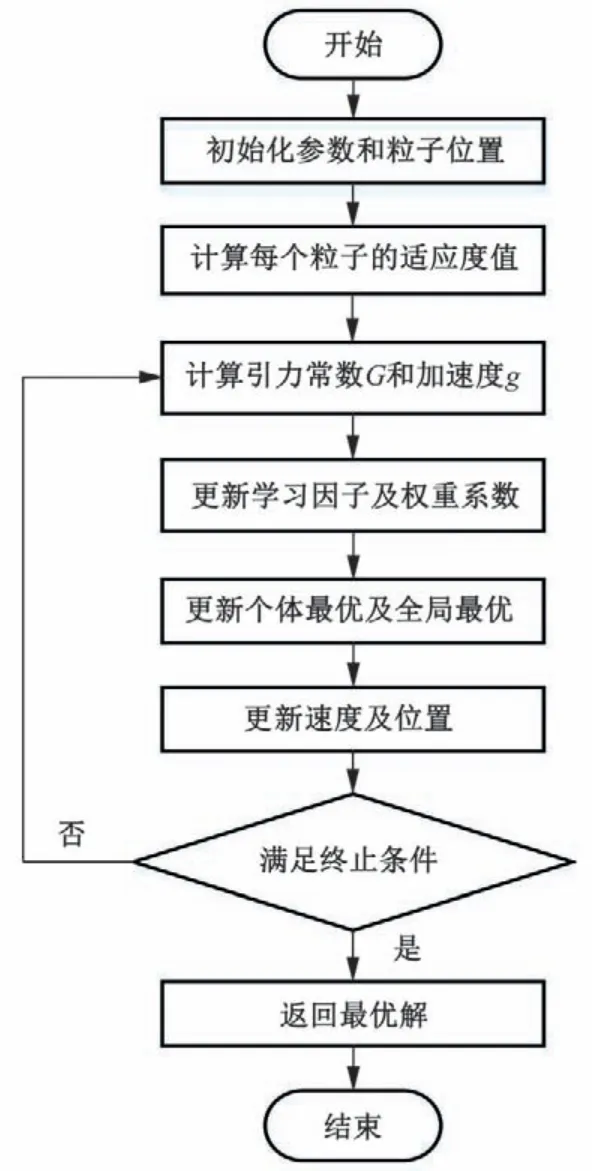
图2 GSA计算流程Fig.2 GSA calculation process

3 仿真验证和结果分析

以某大型水电站为例，验证本文提出的GSA-GPC 应用效果。机组的基本参数为：额定功率700 MW，额定流量432.7 m3/s，最高水头229.4 m，最低水头154.6 m，额定水头197 m。模型的基本参数为：T1v=0.1，Ty=0.46，Tw=1.29，Ta=12.239，eg=0.176。电厂PID控制器参数：KP=0.28、KI=0.2、KD=0。

首先采用GSA 优化6个典型工况下GPC 的超参数，确定N、Nu和α取值分别为58、10 和0.99。然后根据优化得到的超参数，得到这6个工况下GPC 控制器调节效果，与PID 控制器对比情况如图3 所示。从图3 可以看出：在这6 个工况中，GSA-GPC控制器调节时间ts和上升时间tr均低于PID 控制器；GSA-GPC控制器作用下水轮机力矩反调量σ2低于PID 控制器；PID 控制器无超调量σ1，这是由于电厂在设置参数时较为保守；GSAGPC 控制器在其它指标较优的情况下同样无超调量，体现出GSA 算法优化的极佳效果及GPC 在水轮机过渡过程中的调节优势。

综合来看，本文所提出的GSA-GPC 的控制性能优于传统的定PID控制，在不同工况下均能保证最优的控制效果，且该控制器具有强自适应能力和鲁棒性，具有重要的应用价值。

4 结 论

本文针对传统定PID控制器在新型电力系统中难以应对工况多变的缺陷，考虑GPC 优势，提出基于GSA 的GPC 参数优化方法及进一步的基于GSA-GPC 的大型水电机组控制策略。仿真对比试验表明，相比PID 控制器，GSA-GPC 控制器在多工况下均具有更优异的调节性能，及强大的鲁棒性、自适应性。鉴于极佳的控制效果，GSA-GPC在水电机组控制器发展中具有巨大应用前景。