平面钢闸门三维有限元线性分析的若干问题

2023-08-28许中武周建方

中国农村水利水电 2023年8期

许中武，蔡伟，周建方

（河海大学机电工程学院，江苏常州 213022）

0 引言

闸门是用来关闭、开启或局部开启水工建筑物中过水孔口的活动结构，其主要作用是控制水位、调节流量。作为水工建筑物的重要组成部分，闸门的安全性和适用性在很大程度上影响着整个水工建筑物的运行效果［1］，平面钢闸门作为闸门中使用频率最高的类型之一，其设计计算和安全运行也更值得工程设计人员关注。对于平面钢闸门，其设计计算方法有三维有限元方法和传统的平面体系计算方法，目前各大设计院的关于平面钢闸门设计和复核计算方法仍以平面体系计算方法为主。平面体系计算方法先将平面钢闸门简化分解为若干基本构件（如面板、主梁、水平次梁、竖直次梁、顶梁和底梁等），再对每一构件进行设计计算［2］。由于平面体系计算方法忽略了各构件的协同作用，且其计算模型和荷载分配均依据工程经验，可能会造成某些构件的材料浪费或局部偏于危险的现象。

随着三维有限元方法和相关软件的成熟和完善，许多专家学者开始将三维有限元方法应用于平面钢闸门结构计算。同时，美国的《水工钢结构设计》［3］、中国的SL 74-2019《水利水电钢闸门设计规范》［4］（以下简称规范）和NB 35055-2015《水电工程钢闸门设计规范》［5］等相关设计规范均指出，除了使用传统的平面体系计算方法外，三维有限元方法也可供平面钢闸门设计计算使用。但工程设计或科研人员在使用三维有限元方法对平面钢闸门进行分析计算时并没有相应导则可供参考。不同人员对软件操作和三维有限元方法掌握程度的差异，可能导致对同一闸门的计算结果不同，从而降低了计算结果的可信度。为此，亟需平面钢闸门三维有限元分析导则指导设计人员进行相关三维有限元线性分析。目前，已有国内学者对闸门三维有限元分析原则进行了研究。张雪才［3，6］等分别从闸门面板和支臂结构的合理单元类型、单元尺寸或数量等方面展开分析研究，并得出了相应的分析原则。然而，关于闸门三维有限元分析原则的研究目前仍处于初步阶段，并不完善。

本文以某水电站机组进水口快速平面钢闸门为主要研究对象，结合相关设计资料，基于ANSYS有限元分析软件，从有限元网格划分和漏水孔简化两个方面系统研究平面钢闸门三维有限元线性分析时的若干问题，以期相关结论可供工程设计人员在对此类平面钢闸门进行设计计算时提供参考，同时也为我国相关平面钢闸门设计规范的修订和三维有限元线性分析原则的制定提供依据。

1 闸门概况

本文研究的水电站机组进水口快速闸门为平面钢闸门，孔口尺寸为8.8 m×11.0 m（宽×高），底槛高程736.00 m，设计水位827.83 m，设计水头按92.00 m 计算。该平面钢闸门的门叶结构布置图如图1所示，为方便下文阐述相关计算数据，将该平面钢闸门布置的12 根主梁从上到下分别记为1 号到12 号主梁。其中1 号和2 号主梁为箱形结构，记为上节箱形梁；同理11 号和12 号主梁构成下节箱形梁，其余主梁为工形梁；底梁为矩形截面梁，截面尺寸为40 mm×9 960 mm×200 mm。

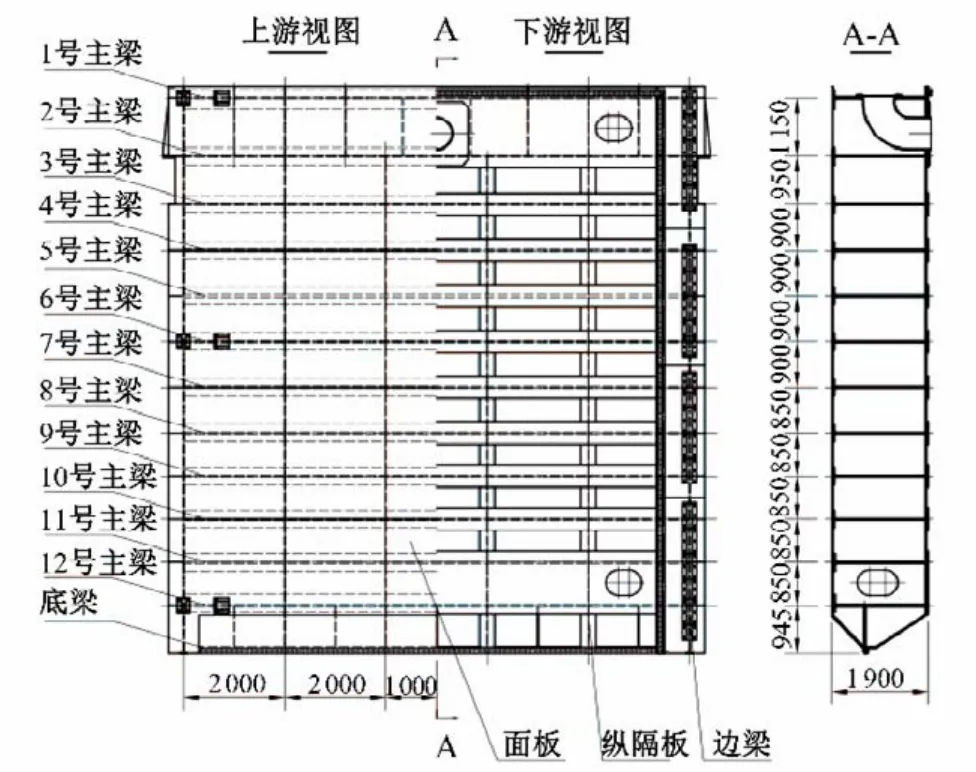
图1 门叶结构布置图Fig.1 Structural drawing of door leaf

2 有限元网格划分

划分网格是建立有限元模型的一个重要环节，所划分的网格形式对计算精度和计算规模将产生直接影响［7］，因此需要考虑多方面因素。在有限元软件中网格划分流程主要包括选定单元属性、设置网格尺寸和选择网格划分方式等，其中单元属性包括单元类型、材料类型和单元坐标系等。目前，在平面钢闸门有限元模型的单元类型选定、网格尺寸设置和网格划分方式选择等方面的相关依据和研究较少，科研和工程设计人员多凭经验划分网格。本节将从上述3个方面对平面钢闸门有限元模型的网格划分进行讨论。

2.1 单元类型

对于平面钢闸门这样典型的空间薄壁结构，为保证计算精度，在建立其有限元模型时应尽量建立完整空间薄壁结构。此时，平面钢闸门所有构件均采用壳单元划分网格。合理的壳单元类型将决定结构应力和挠度的计算精度。文献［6］以平面钢闸门面板区格的几种计算模型为例，分别验证了ANSYS软件中分析薄壁结构常用壳单元的计算精度。然而，文献［6］仅比较了使用不同单元类型时计算模型挠度的有限元解和理论解，实际上，在平面钢闸门结构分析时，保证其强度符合规范要求同样重要。另一方面，文献［6］中的计算模型仅讨论了平面钢闸门面板区格，而实际上平面钢闸门主梁的简支梁模型在设计计算中也很常见。

由于ANSYS 在近几个版本已将shell43 和shell63 单元从图形用户界面操作选项中淘汰，因此本文将选用当前版本中常用的shell181 和shell281 单元。shell181 和shell281 单元均适合对薄的及具有一定厚度的壳体结构进行分析，shell181 单元使用一次插值函数，由4 个结点组成，每个结点具有6 个自由度；shell281 单元则使用二次位移插值函数，由8 个节点组成，各节点自由度与shell181相同。

平面钢闸门的平面体系计算方法一般将主梁视为简支梁模型，将面板区格视为四边固定矩形弹性薄板模型，下面将使用这两种常用计算模型，比较shell181和shell281这两种单元类型在应力和变形上的计算精度。在ANSYS 中分别建立相应的计算模型，两种模型的材料参数均依据Q355B 确定。其中，简支梁截面尺寸为0.3 m×0.05 m（梁高×板厚），支承长度为10 m，均布荷载为10 kN/m；四边固定矩形弹性薄板尺寸为2 m×1 m×0.05 m（板长×板宽×板厚），均布荷载为0.5 MPa。据此建立的计算模型如图2所示。

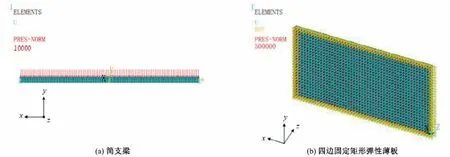
图2 有限元计算模型Fig.2 Finite element calculation model

对于受均布荷载的简支梁，其应力和最大挠度可根据材料力学公式直接求得。对于受均布荷载的四边固定矩形弹性薄板，其应力计算可依据规范和弹性力学理论［8］；在计算其挠度时，根据弹性力学理论可知，在长边与短边之比为2 时，矩形薄板的最大挠度理论解w为［9］：

式中：q为均布荷载；a为短边长度；E为弹性模量，取2.1×106MPa；h为薄板厚度。

对受均布荷载的简支梁和四边固定矩形弹性薄板模型，在划分网格建立有限元模型时，分别选用shell181 和shell281 单元，且单元尺寸设置等均相同，计算后提取相应结果，并与理论解比较，如表1和表2所示。

表1 简支梁计算结果Tab.1 Calculation results of simply supported beam

表2 四边固定矩形弹性薄板计算结果Tab.2 Calculation results of rectangular elastic thin plate with four edges fixed

由表1 和表2 可知，在荷载、约束和网格尺寸等其他设置相同的情况下，对于简支梁和四边固定矩形弹性薄板模型，shell281 单元无论在应力还是变形计算上精度都更高。以简支梁最大正应力为例，使用shell181 单元的有限元解相对于理论解误差为-20.23%，而shell281 单元有限元解误差仅为-0.06%。特别地，从四边固定矩形弹性薄板的计算结果可知，选用两种不同的单元类型对挠度计算结果影响不大，与文献［6］的结论一致，说明了上述计算结果的正确性。但是比较应力计算结果的理论值和有限元解，shell281 单元的精度显著提高，相差一个量级，计算时间相差不大。因此对平面钢闸门这样的空间薄壁结构进行有限元计算时应优先选取shell281单元。

2.2 网格尺寸

有限元模型网格尺寸对计算精度影响较大，模型网格尺寸的减小在一定程度上会提高计算精度，但当网格尺寸减小到一定程度时，精度提高会很有限，而计算时耗却会大大增加。此时，可以认为网格尺寸对计算精度的影响可以忽略不计，即有限元计算结果与网格尺寸之间具有无关性。在平面钢闸门有限元计算时，获取网格无关性的解是工程设计或科研人员需要关注的关键问题。本文将选取shell281 单元，计算分析不同网格尺寸下的平面钢闸门有限元模型，探讨适用于本文所研究的平面钢闸门的合理网格尺寸范围。

分别建立7 种不同网格尺寸的平面钢闸门有限元模型，各模型的网格尺寸如表3 所示。本文在建立有限元模型时，使用ANSYS 默认的全局直角坐标系（笛卡尔全局坐标系），其中x轴沿平面钢闸门跨度方向，y轴沿平面钢闸门高度方向，z轴沿水流方向，坐标原点位于平面钢闸门竖板底部中点处。

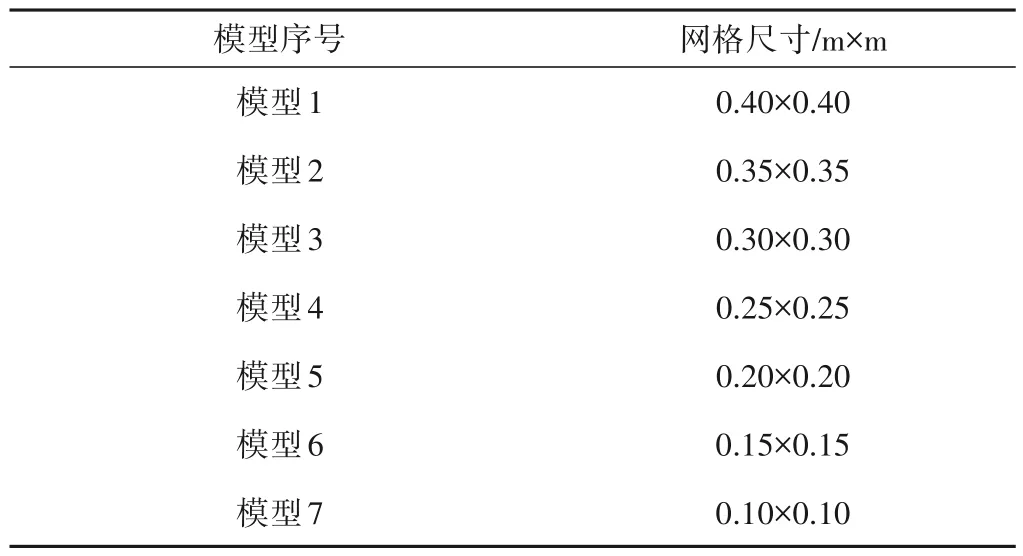
表3 模型尺寸分组Tab.3 Model size grouping

该平面钢闸门采用Q355B 材料，计算时材料弹性模量E取2.06×105MPa，密度ρ取7 850 kg/m3，泊松比v取0.3。平面钢闸门作用水头按设计水头设置。此外，1 号主梁腹板承受额外的垂直水柱压力。根据平面钢闸门实际工作状况，滑块上受水流方向约束（Uz=0），平面钢闸门底部受铅直方向约束（Uy=0）。为保证计算模型的几何不变性，假定平面钢闸门底部中点沿跨度方向无位移（Ux=0）。下文所有平面钢闸门有限元计算的荷载、相关参数和约束设置均相同。

以网格尺寸为0.40 m×0.40 m 的模型1 为例，计算后得到的整体等效应力和变形云图如图3 所示，提取所有平面钢闸门模型中主要构件的最大等效应力和挠度列于表4和表5。

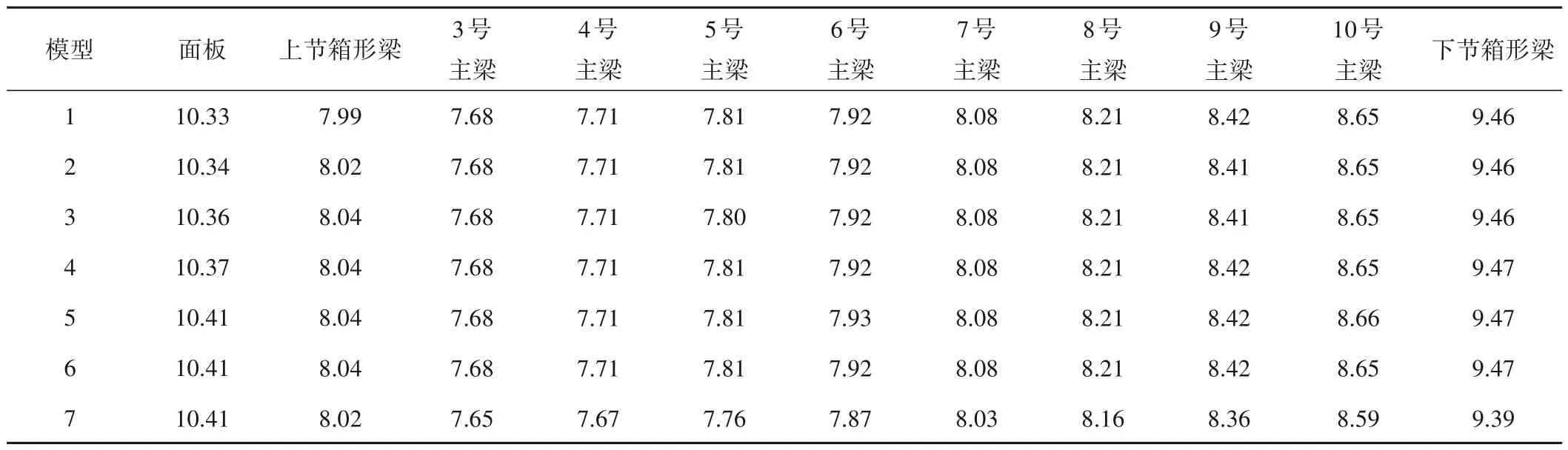
表5 平面钢闸门主要构件最大挠度mTab.5 Maximum deflection of main components of plane steel gate

图3 模型1有限元计算结果Fig.3 Finite element calculation results of Model 1

由表4和表5可知：①随着网格尺寸的减小，平面钢闸门面板和各主梁的最大等效应力呈现增大趋势，最大等效应力出现位置均相同，但网格尺寸对面板最大等效应力影响最大。对于面板，从模型1 到模型4，即网格尺寸从0.40 m×0.40 m 到0.25 m×0.25 m 时，面板最大等效应力增长平缓；但从模型4 到模型5，即网格尺寸从0.25 m×0.25 m 到0.20 m×0.20 m 时，其最大等效应力增长率最大，达到7.56%；从模型5 到模型7，即网格尺寸小于0.20 m×0.20 m 时，面板最大等效应力继续增长平缓，趋于收敛。此时，可以认为网格尺寸和平面钢闸门面板最大等效应力计算结果具有无关性。②网格尺寸对平面钢闸门主要构件挠度影响很小。各模型面板和主梁最大挠度偏差较小。以面板为例，随着网格尺寸的减小，各模型最大挠度增长率最大仅为0.39%，即在网格尺寸小于0.40 m×0.40 m 时，网格尺寸和平面钢闸门主要构件最大挠度计算结果即具有网格无关性。综上，在对本文所研究的平面钢闸门进行有限元计算时，其合理网格尺寸应小于或等于0.20 m×0.20 m。

2.3 网格划分方式

对于面，ANSYS 为用户提供了两种网格划分方式：自由网格划分和映射网格划分。自由网格划分通常由有限元计算软件自动划分，易出现畸变网格和退化网格［10］。而映射网格划分则需满足特定规则，具有规则形状且明显成排。一般映射划分得到的网格质量优于自由划分得到的网格质量，映射划分有限元模型的计算精度理论上也优于自由划分有限元模型的计算精度。将映射划分应用于平面钢闸门有限元模型的建立上，需要在前期投入大量工作，对某些复杂的面需要进行切割，对各个面也只能逐一划分网格。如果映射划分方法对平面钢闸门在应力和挠度的计算精度上提高甚微，则会得不偿失。

本文使用shell281单元，网格尺寸设置为0.10 m×0.10 m，分别对该平面钢闸门进行自由网格划分和映射网格划分，生成的局部有限元模型如图4 所示，其中自由网格划分得到的有限元模型出现了大量退化网格。两种网格划分方式所得有限元模型的单元数和节点数如表6所示。

表6 平面钢闸门有限元模型节点和单元数Tab.6 Node and element number of plane steel gate finite element model

图4 平面钢闸门局部有限元模型Fig.4 Local finite element model of plane steel gate

经有限元计算后提取平面钢闸门主要构件的最大等效应力和挠度列于表7。

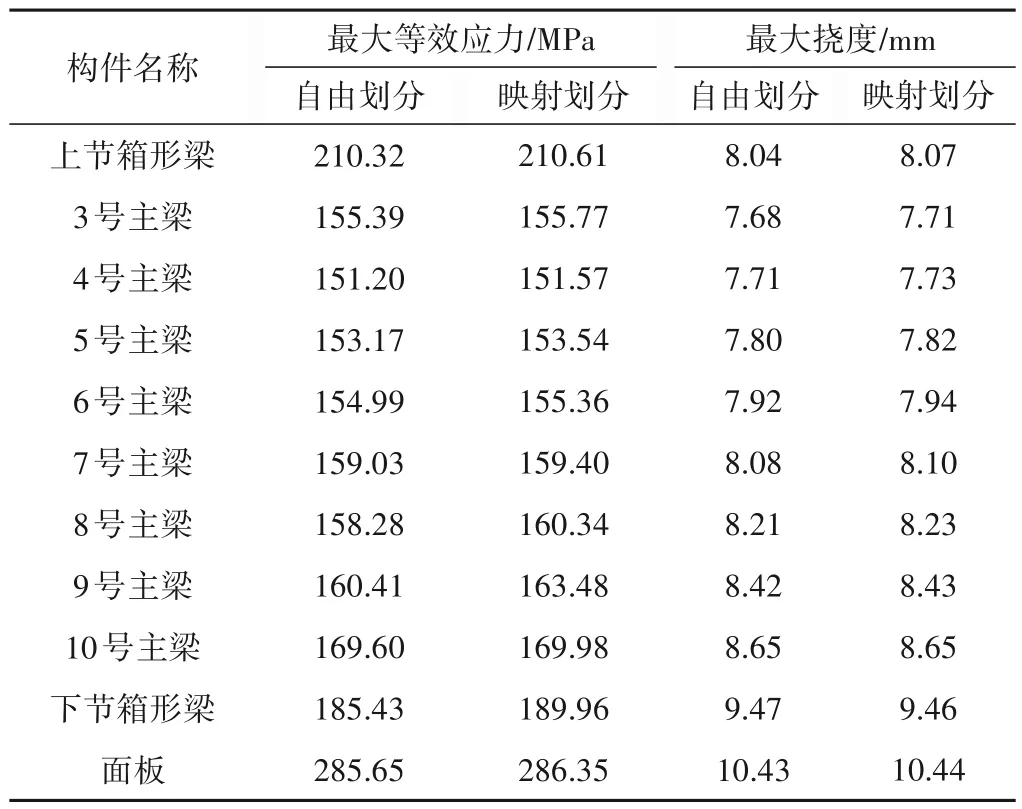
表7 平面钢闸门主要构件应力和挠度计算结果Tab.7 The stress and deflection calculation results of the main components of plane steel gate

两种网格划分方式下，计算得到的平面钢闸门整体的应力和变形分布均类似，最大等效应力和最大变形值偏差较小。由表7可知：与映射划分模型相比，平面钢闸门各主梁和面板在自由划分下的最大等效应力值误差仅为-3.38%，最大挠度误差不超过1%，即无论是应力还是变形，两种划分方式下的计算结果相对误差都很小。

但实际上，在使用映射划分方式时，平面钢闸门有限元模型的单元数和节点数都更多，计算规模更大，并且映射划分在前期建立模型阶段还需要花费大量时间和精力。此外，虽然通过映射划分方式得到的网格质量更佳，但从计算结果来看精度提高并不明显。因此使用有限元方法对此类平面钢闸门进行计算分析时采用自由划分方式即可。

3 漏水孔结构简化

由于平面钢闸门结构复杂，构件众多，细节特征也较多，因此在有限元软件ANSYS中建立其模型时通常需要适当简化，使模型与计算机性能和分析目的相匹配。简化平面钢闸门模型一方面可以减小有限元求解的规模，提高计算效率，另一方面也可以降低工程设计或科研人员在前期的建模工作量。

为了防止平面钢闸门各主梁上的积水影响启闭甚至导致其构件锈蚀，进而影响平面钢闸门结构性能，主梁腹板上一般会开设有漏水孔。如果漏水孔对平面钢闸门应力或变形计算影响不大，则可在建模阶段忽略这些漏水孔，减小有限元分析工作量，提高效率。

本文研究的平面钢闸门在主梁腹板上开设有若干直径为200 mm的漏水孔，其中2号至11号各节主梁腹板分别均匀布置6 个，12 号主梁腹板均匀布置8 个。根据规范，一般主梁腹板应尽量避免开大孔，漏水孔直径Ф与主梁截面高度（下文简称“梁高”）H之比（下文简称“径高比”）应小于0.5，必要时还需对漏水孔采取补强措施，保证结构强度。因此漏水孔的孔径尺寸是判断其是否可以简化的重要参数。

本文将针对该平面钢闸门，在保持漏水孔位置不变的情况下，分别建立径高比为0.1、0.15、0.2、0.25和0.3的平面钢闸门模型，相应的孔径和梁高参数设置如表8所示。同时，还建立了无漏水孔的平面钢闸门模型，用以与相应的计算结果对比。开展有限元计算并提取平面钢闸门主梁应力和挠度的计算结果，统计绘制出图5和图6。

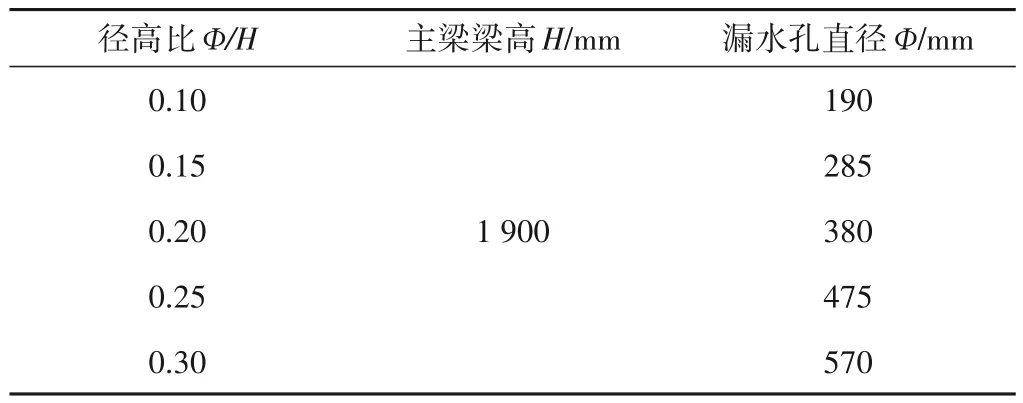
表8 孔径和梁高设置Tab.8 Setting of aperture and beam height

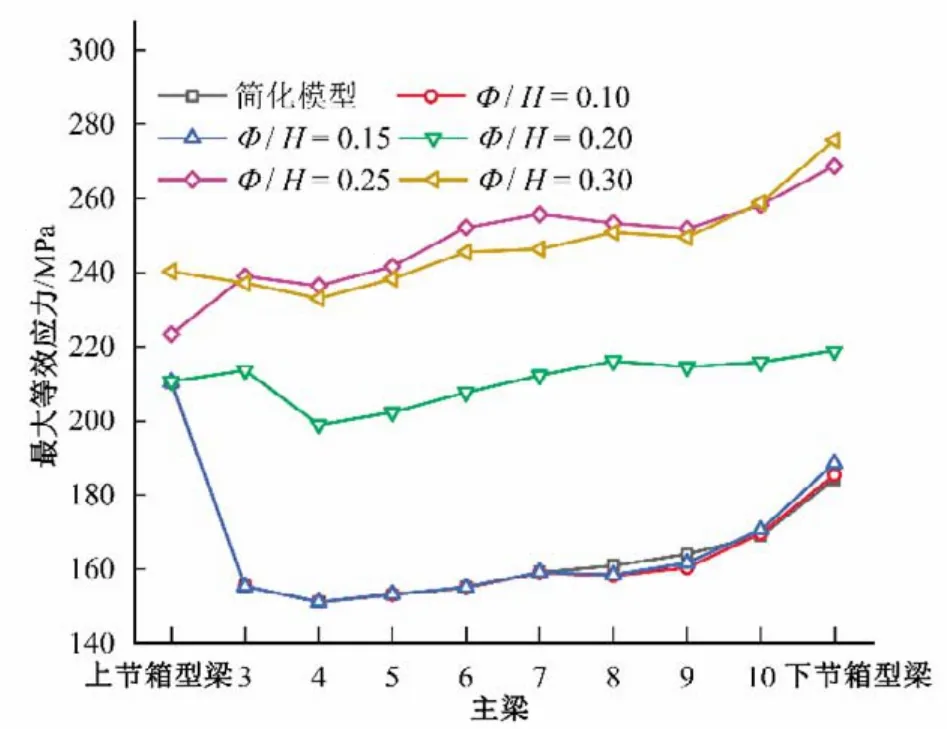
图5 各模型主梁最大等效应力Fig.5 Maximum equivalent stress of main beam for different models

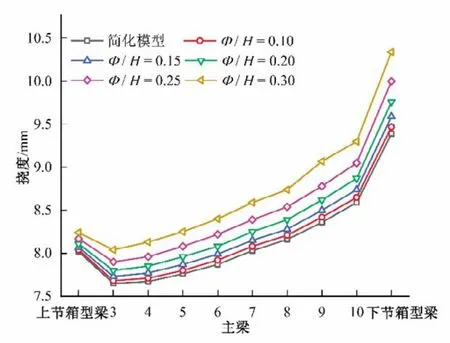
图6 各模型主梁最大挠度Fig.6 Maximum deflection of main beam for different models

由图5 和图6 可知：①在径高比为0.1 到0.15 时，各模型主梁最大等效应力值之间相差很小，出现的位置相同，且各组计算结果与简化模型计算结果基本相同；在径高比为0.2 到0.3时，各计算组主梁在两侧漏水孔附近均出现了较为明显的应力集中现象，且奇点应力值大于简化模型主梁最大等效应力，并随径高比的增大而增大，部分主梁两侧漏水孔附近奇点应力超出相应的许用应力；②不同径高比模型的主梁最大挠度均出现在跨中位置，与简化模型计算结果发生的位置相同。随着径高比的增大，主梁最大挠度相对偏差逐渐增大。最大偏差出现在径高比为0.3模型的下节箱形梁，为10.12%，但各模型主梁挠度都满足规范设计要求。

综上，当径高比小于或等于0.15 时，在建立平面钢闸门有限元模型时可忽略主梁腹板漏水孔，简化模型；而当径高比大于0.15 时不可忽略漏水孔，并且需要根据有限元计算结果采取相应的补强措施。