冻融循环对渠道保温材料导热性能的影响

2023-08-28朱顺元

中国农村水利水电 2023年8期

朱顺元，明锋

（1. 青海省湟源公路工程建设有限公司，青海西宁 810000；2. 中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃兰州 730000）

0 引言

混凝土渠道衬砌防渗因其具有成本低、水资源利用率高等优点，逐渐成为农业灌溉的主要方式［1］。然而，在广大季节冻土区，大多数渠系水工建筑物存在一定的冻胀破坏［2］。为减少渠底及渠坡土体冻胀引起的冻害，通常在混凝土面板下铺设一定厚度的保温材料［3，4］。然而，在进行保温材料厚度设计时，一般将保温材料的导热系数设为常数。由于忽略了环境因素对其导热性能的劣化，这将高估材料的保温性能［5］。为减少因设计缺陷造成的渠道冻胀破坏，需要对保温材料导热性能变化进行分析，以此为渠道保温层设计提供参考。

温湿度会改变保温材料的导热性能，而冻融作用将加剧这一过程［6］。保温材料是一种典型的多孔介质，具有一定的吸水性。水分进入保温材料后，将发挥“热桥”作用，使得保温材料导热系数增大。在较大相对湿度条件下，保温材料达到平衡时的含水率越大［7］，导热系数的增幅也越大［8］。对于铺设在冻土区的保温材料，还将经历冻融作用［9］。研究表明，冻融作用将改变材料孔隙结构，进而导致其物理力学性质发生变化［10，11］。汤贵海等发现随着经历冻融次数的增加，聚氨酯内部气孔泡破损率增加，吸水率可达到700%［10］。当经历30次冻融后，聚苯乙烯泡沫板的导热系数增大71.43%，抗压强度则降低了36.11%；聚氨酯泡沫板的导热系数增大47.06%，抗压强度则降低了38.46%［12］。丁杨等发现经历112 次浸水冻融试验后，聚氨酯泡沫的导热系数增大33.12%，泡沫混凝土的导热系数增大24.09%［13］。上述研究均表明，冻融作用会增大材料导热系数，但在经历200 次冻融后，材料吸水率仍然没有达到饱和［11］。这就意味着，材料再次经历冻融循环作用后，其吸水率和导热系数将继续增大。

上述研究表明，冻融作用将增大保温材料导热系数，但不同材料对冻融的响应不同。为建立吸水率与导热系数的关系，以保温材料的三相组成为基础，利用传热理论建立导热系数预测模型，并引入体积修正参数来提高模型预测精度。通过与试验结果和既有模型对比，验证模型的有效性。以期为有效预测冻融作用下的保温材料导热系数提供一种有效方法，进而为渠道保温层设计提供准确参数。

1 导热系数试验

1.1 试验材料与方法

渠道保温材料需要承担一定荷载，所以多采用挤塑聚苯乙烯板（XPS 板）为保温材料［2］。因此，选择市售XPS 板为试验材料［图1（a）］，其基本性质如表1所示。

图1 试验材料与设备Fig.1 The experimental material and the equipment

表1 保温材料基本性质Tab.1 Parameter of these insulation materials

先对规格为300 mm×300 mm×30 mm 的保温板试样进行编号，并把试样放入50 ℃的烘箱中进行烘干，以获得干燥试验。24 h 后可认为试样已经干燥，待冷却至室温再称重。然后，参照《普通混凝土长期性能和耐久性能试验方法标准》（GB/T50082-2009）中的快速冻融方法，依据《建筑用绝热制品抗冻融性能的测定》（GB/T 33011-2016）的要求，开展XPS 板冻融试验。

冻融吸水试验在TDFR-3 型混凝土快速冻融试验机中完成。首先，将保温板放入自制铁箱中，并向箱内加入蒸馏水，直到水面高出保温材料顶面约5 cm。然后，将铁箱放入冻融循环试验箱内，利用冻融循环试验箱内的不冻液对铁箱内的试样进行冻结或融化。最后，设置冻融循环，试验温度从+20 ℃降至-20 ℃，再升至+20 ℃时为一个冻融循环。其中，冻结4 h，融化2 h，即一个冻融循环耗时6 h。每冻融25 次后，取出试样进行测试。擦去试样表面水分，采用精度为0.01 g 的电子天平称取保温材料质量，然后采用智能型双平板导热系数仪［图1（b）］测试保温材料在20 ℃下的导热系数。

1.2 试验结果

1.2.1 吸水率变化

图2给出了XPS板质量吸水率随冻融次数的变化关系。未冻融条件下，XPS 板的质量吸水率为0.68%。冻融200 次后，其质量吸水率为4.53%（图2）。冻融200 次后的吸水率较冻融前增大5.7倍。从图2中还可发现，XPS 板的吸水率随冻融次数表现为线性增长关系，拟合关系符合y=0.019x+0.619 1。由于聚苯乙烯分子结构本身吸水性较差，加之XPS 板具有大量的封闭孔隙，外界水分难以进入XPS 板内部，所以冻融前的吸水率较小。在周期性冻融作用下，XPS 板内部的水分在冰-水相态间不断转变，导致其孔隙结构发生破坏，形成开孔孔隙，水分得以进入材料内部。随着冻融次数的增加，XPS 板的开孔率越来越高，进入XPS 板内部的水分逐渐增多，表现为XPS 板吸水率逐渐增大。因此，应采取有效措施提高保温材料的闭孔率和抗冻融性，从而降低其吸水率。

图2 XPS板吸水率随冻融次数变化规律Fig.2 Variation of the moisture content with the freezing-thawing cycles

1.2.2 导热系数变化

图3 中可以看出，XPS 板导热系数几乎随吸水率呈线性关系增加。冻融200次后，XPS板的导热系数从0.032 W/（m·K）增大到0.045 8 W/（m·K），增幅约43%。这是因为在干燥状态下，保温材料依靠固体骨架和空气进行传热，因此闭孔率高的保温材料具有优异的绝热性能。当水分进入保温材料后，可看作是导热系数大的水取代了导热系数小的空气。由于水的导热系数是空气的20 多倍，所以即使进入XPS 板内部的水分较少，也可增大XPS 板的导热系数。此外，孔隙中的水分能够发挥“热桥”作用，缩短传热路径，同样可增大XPS 板的导热系数。值得注意的是，冻融200次后，XPS板的吸水率曲线仍然保持直线增长趋势，这表明XPS板仍未达到饱和。若再增加冻融次数，XPS板的吸水率及导热系数仍将继续增大。然而，在大多数热工计算中，保温材料的导热系数被认为是一个固定值。这将高估保温材料的保温性能，从而达不到预期的防冻效果。因此，建议提高保温性能安全系数，以补偿因保温材料导热系数增大所需厚度。

图3 XPS板导热系数随吸水率变化规律Fig.3 Variation of the thermal conductivity with moisture content

图3 给出的是导热系数与吸水率的关系，而不是导热系数与冻融次数的关系。这是因为不同材料对冻融作用的响应不同，使得其在吸水性能方面也表现不同。水分是影响材料导热系数的关键因素，所以建立吸水率与导热系数的关系更符合实际情况。室内试验只能得到部分吸水率下的导热系数，为了得到任意吸水率下材料的导热系数，需要建立更具普遍性的导热系数模型。

2 导热系数模型

2.1 既有导热系数模型

依据多孔介质内部结构特征，研究者们利用类比电阻法来计算材料等效热阻，进而求得导热系数［14］。其中，最常见的方法是使用串联、并联思想求解多孔介质的等效导热系数。此处列出3个经典导热系数模型［15］：

并联模型：

串联模型：

Maxwell模型：

式中：λc为连续相的导热系数；λd为分散相的导热系数；ϕ为分散相体积分数。

研究表明，既有导热系数模型仅考虑各组分导热系数及其体积分数对导热系数的影响，使得模型计算结果与实测结果存在较大误差［14］。为此，需要建立一个预测精度更高的导热系数模型。

2.2 新建三相导热系数模型

为简化导热系数计算过程，根据保温材料多孔结构特征，做出如下假设：

（1）含湿保温材料为均质体，固体颗粒、水分和空气均匀分布在单元体内；

（2）不考虑对流、辐射以及接触热阻对传热过程的影响；

（3）以边长为2c的单元体为研究对象，将球半径为a的固体颗粒置于单元体八个角落，而球半径为b的水分则居于单元体中心，单元体剩余体积则为空气。

以坐标系为对称轴，将边长为2c的单元体划分为8 个大小相同、边长为c的小单元体［图4（a）］。根据固体颗粒和水分的位置关系，可将图4（a）的小单元体划分为3个区域：①0 ≤x≤a为区域I，由固体颗粒与空气组成，对应的导热系数λI；②a＜x＜b-c为区域II，仅有空气，对应的导热系数λa；③b-c≤x≤c为区域III，由空气与水分组成，对应的导热系数λIII。

图4 热阻模型示意图Fig.4 Schematic diagram of the thermal resistance model

考虑到区域I 与区域III 的导热系数计算方式相同，将以区域I 为对象，对其导热系数计算过程进行详细说明。具体求解思路如下：首先将区域I 切成厚度为dx的薄片［图4（b）］，然后将薄片切成宽度为dz的条带。在导热系数分析过程中，则首先分析条带导热系数，再将条带集合成薄片，最后将薄片集合成单元体，最终得到单元体的导热系数。

根据图4（c），固体颗粒的体积分数ϕs可以表示为：

式中：y为变量，其取值为0～a。

空气的体积分数ϕa可表示为：

根据假设，热流垂直于Y-Z平面，图1（c）中的两个热阻属于并联关系，则该条带的导热系数λ1可以表示为［17］：

式中：λs为固体材料的导热系数；λa为空气的导热系数。

对于图4（b）中的薄片，根据体积分数，则可得到其导热系数表达式：

由于固体颗粒呈球状，导致λ1在Z轴方向的数值有所不同。因此，在式（7）中引入λ1的平均值λ1av，具体表示为：

将式（8）带入式（7）中：

区域I的平均导热系数可表示为：

将式（9）带入式（10）中，整理可得：

根据球半径与坐标的关系：

将式（12）带入式（11）中，则区域I 的平均导热系数可表示为：

采用同样方法，可得区域III的平均导热系数：

式中：λw为水的导热系数。

如图4所示，3个区域属于串联关系。根据3个区域的体积关系，可得单元体导热系数：

根据几何关系，得到固体、水分的体积分数分别为ϕ1和ϕ2，

将式（16）和（17）带入（15）中，得到以体积分数为变量的多孔介质导热系数表达式：

式（18）仅考虑了材料各组分的体积分数及其导热系数，忽略了传热路径、界面热阻以及不同相之间导热性能的差异。根据最小热阻理论，热流总是沿热阻最小路径传递，并非是完全沿固定方向传递［18］。这些差异将导致预测结果与实测结果存在较大偏差，为此，建议引入参数对体积分数进行修正，以提高模型预测精度。

依据文献［19］的方法，将固体和水分视为连续相，空气视为分散性，则有：

式中：K1和K2为比例系数。

固体、水分修正后的体积分数ϕ1′和ϕ2′可分别表示为：

式中：m和n为拟合参数。

将式（20）带入式（18），即可得到修正后的三相复合材料导热系数模型。当ϕ2= 0 时，则该三相导热系数模型退化为两相导热系数模型，适用于干燥保温材料导热系数预测。

2.3 模型评价方法

为了评价各模型的预测效果，采用最大相对误差（ME）和均方根误差（RMSE）来评价各模型的优劣。最大相对误差和均方根误差分别表示为：

式中：N为数据对总数；i为当前数据对；为实测导热系数；为预测导热系数。

3 模型验证

3.1 验证试验结果

取空气导热系数为0.023 W/（m·K），水分导热系数0.62 W/（m·K）。厂家给出XPS 板孔隙率为0.23，固体导热系数为0.48 W/（m·K）。将参数带入提出的导热系数模型，结合图3 的实测结果，可求得拟合参数m和n。将拟合参数m和n带入模型，即可得到导热系数预测值［图5（a）］。导热系数预测值与实测值的变化趋势一致，最大相对误差为3.84%（表2），相关系数达到0.97。由此可见，模型能够有效反映吸水率对XPS 板导热系数的影响，可用来预测XPS板的导热系数。

图5 不同保温材料的导热系数预测值与实测值Fig.5 Predicted and measured thermal conductivity of three insulation materials

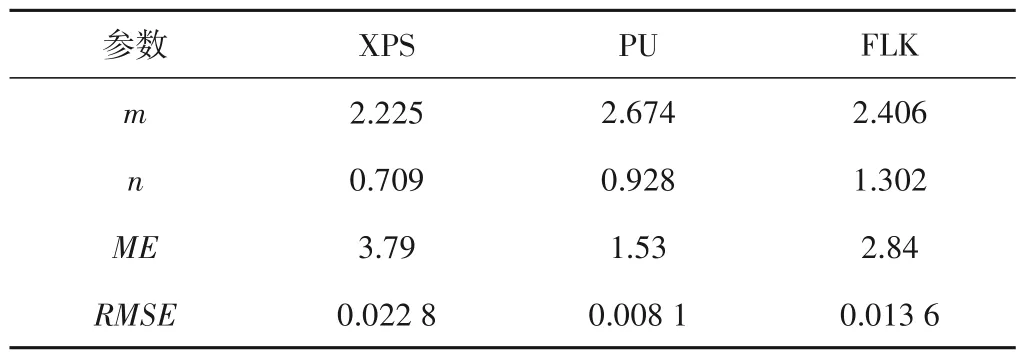
表2 模型预测误差分析Tab.2 Prediction error of the model

为检验新建模型的普适性，选择文献［20］中的聚氨酯（PU）和聚酚醛（FLK）导热系数试验结果，对模型进行验证。如图5（b）所示，模型能够反映PU 和FLK 这两种保温材料导热系数随吸水率的变化趋势。因为模型中有两个可调参数，所以导热系数预测值与实测值的最大相对误差仅为2.84%。表2 结果表明，均方根误差整体处于较低水平，表明预测模型的稳定性。三种保温材料的导热系数预测值与实测值对比结果表明，模型具有较高的准确度，最大相对误差小于5%。与材料导热系数实测值的对比结果表明，本文模型具有一定的普遍适用性。

3.2 与既有模型对比

利用连续-分散两相导热系数模型计算XPS 板的导热系数时，先将水分视为连续相、空气视为分散相，确定含湿空气的导热系数。再将固体颗粒视为连续相，含湿空气视为分散相，即可得到保温材料的导热系数。串联模型、并联模型、Maxwell 模型、本文模型预测值与实测值的对比结果如图6 所示。所有模型的预测结果均显示，保温材料导热系数随吸水率的增大而增大，但增加速率有所不同。串联模型预测值的增速最小，其次是Maxwell 模型，最大为并联模型及本文模型。需要注意的是，并联模型、串联模型及Maxwell 模型的预测值与实测值偏差较大，而新建模型预测值与实测值吻合较好（图6）。这主要因为3个经典导热系数模型中，仅考虑了材料组分的导热系数及体积分数，而忽略了热流传递方向、孔隙形状、传热路径、界面热阻等因素对导热系数的影响。新建模型不仅考虑了各组分的导热系数及其体积分数，而且采用了并联与串联组合方式计算导热系数，在一定程度上考虑了热流方向对导热系数的影响。此外，本文模型拥有两个可调整的参数。这两个可调参数在一定程度上反映了热流传递方向、孔隙形状、传热路径、界面热阻等因素对导热系数的影响，所以本文模型的预测精度更高。

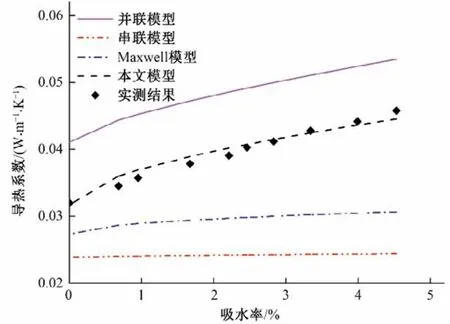
图6 不同模型对XPS板导热系数的预测结果Fig.6 Prediction results of thermal conductivity of XPS by different models

在本文提出的导热系数模型中，引入两个拟合参数分别对固体体积和水分体积分数进行修正。为更好的展示两个拟合参数对导热系数预测值的影响，图7 给出了仅改变m或n条件下的导热系数变化（以XPS 板参数为基础）。参数m决定了干燥状态下保温材料的导热系数，参数n则反映的是吸水率对导热系数的影响程度。当样品吸水率为0 时，导热系数随着m的增大而减小，但减小速率在逐渐减小。当m≥4后，增大m对导热系数的影响较小。在固定m的前提下，导热系数随着n的增大而减小。即n越大，表示吸水率对导热系数的影响程度越低。实验结果表明，当吸水率增大1%时，XPS、PU 和FLK 的导热系数依次增大0.003 04，0.002 67和0.000 10 W/（m·K）。吸水率对FLK板导热系数的影响程度最低，所以对应的n越大（表2）。