无管勘资料山地城市暴雨内涝模拟方法研究

刘 非，李陪然，陈 垚，袁绍春，刘 臻，曾梓健，任春娇，刘 俊，张 茅，朱俊成

（1. 重庆交通大学河海学院，重庆 400074； 2. 重庆交通大学环境水利工程重庆市工程实验室，重庆 400074；3. 中建二局重庆建设发展有限公司，重庆 401329； 4. 中国建筑第二工程局有限公司，北京 100160）

0 引 言

气候变暖和人类活动改变了自然界的水文循环，增加了极端水文事件发生的概率，突发性暴雨引发的城市内涝问题日益严重，给我国人民的生命财产安全带来严重威胁。

随着计算机技术和模型理论的不断发展，数值模型在城市内涝治理和人员防灾中扮演越来越重要的角色。基于物理过程的雨洪模型可以较好再现和预测研究区内涝发生规律，提供较完整的积水范围、水深、浸水时间等洪水时空要素信息，对防洪管理和应急减灾意义重大。雨洪模型的准确性和运行效率通常受到诸多因素影响，比如输入数据的完整性和精确性、计算区域大小和排水系统规模，以及计算设备和模型算法的先进性等。目前，国内外使用较广泛的一维管网模型有美国环保局开发的暴雨径流管理模型（Storm Water Management Model，SWMM）［1］，二维水文水动力模型软件有InfoWorks ICM、MIKE Urban 等。在众多开源或半开源二维水动力模型中，LISFLOOD-FP 模型具有学习成本低、计算效率高的优点，但在国内推广使用不多［2，3］。无论采用哪一款模型，管网资料通常都是进行城市内涝模拟分析的重要基础数据，因其特殊性和涉密性，往往不易获得。因而，无管勘资料背景下的城市内涝模拟技术是当下雨洪管理领域的一个热点和难点。

近年来，已有部分学者对此进行了探索和尝试，并总结出了目前较为常用的管网替代方法，针对研究区完全没有管网数据的情形，主要以下渗等效法和降雨率折现法［4，5］为主，前者包括雨水井等效排水法、道路等效排水法、全域等效排水法等；对于研究区域尚有部分管网资料，但不完整的情况，除了下渗等效法外，还有管网概化法等。杨东等［6］以陕西省西咸新区为研究区，对比了不同下渗等效法和降雨率折现法，并指出雨水井等效排水法的实际效果最佳。杜佳锴等［7］以粤港澳大湾区某流域为研究区，探讨了降雨率折现法、下渗增加法和管网概化法的适用性。以上方法中，下渗等效法为代表的管网替代方法对数据依赖程度最低，且可通过调整下渗量对模型准确性进行调整，在无管网资料地区具有良好适用性；降雨率折现法由于是将降雨量降低达到替代管网排水作用，极易导致模拟的内涝程度较实际偏低。在下渗等效法中，雨水井等效法在模拟积水面积准确度上最优［6］。但既有的研究较少有提供高效准确的雨水检查井数据获取方法，并将其应用到开源或半开源模型中（例如LISFLOOD-FP 模型），形成从基础数据获取到构建模型的完整技术方法流程。若采取人工实地调查获取检查井位置的方式，当研究区域范围较大时，会有成本过高和效率较低的缺点。因此，亟需一种基于较便捷的检查井数据获取方式和开源（或半开源）模型的无管勘资料地区雨洪模拟技术。

为解决城市内涝模拟研究中管网资料缺失的问题，本文以山地城市重庆某排水分区为研究区域，利用百度地图开放平台提供的全景静态API 功能，对街道检查井进行识别和定位。在此基础上，发挥LISFLOOD-FP 模型计算高效的优势，采用雨水井等效排水法进行雨洪建模，对不同暴雨情景下的研究区内涝积水面积、积水量、积水分布等进行分析。模型采用直接降雨法进行全水动力地表径流计算，并与SWMM 耦合考察桥面径流对局部内涝的影响。所提出的模拟计算方法可为类似无管勘资料山地城市区域利用LISFLOOD-FP 模型进行暴雨内涝风险高效评估提供参考。

1 模型方法与数据

1.1 研究区域及地形

研究区域位于重庆市主城南岸区某排水分区，面积约4.98 km2，如图1（a）所示，北面通过菜园坝大桥和重庆长江大桥与渝中区相连，在南北交通上具有十分突出的地位。根据《南岸区城市内涝治理系统化实施方案》和《中心城区排水防涝专项规划（修编）》，该片区存在多处易涝点，对城市交通运行构成不利影响。由于缺少高精度的地形资料，研究区地形数据从地理空间数据云平台免费获取（https：//www.gscloud.cn/home），空间分辨率为30 m。

图1 研究区域范围和地形Fig.1 The study area and topography

1.2 降雨数据

采用国内雨洪模拟研究中适用性良好的芝加哥降雨过程线［8］进行暴雨情景设计。考虑到国内洪涝规划标准中对于重现期的取值一般不超过百年一遇，而诸如2021年“7·21”郑州极端暴雨事件发生的几率在气候变化背景下呈逐渐上升趋势，因此，本研究中增加了500年一遇降雨情景作为极端情况，设计降雨重现期包括1、5、20、50、100、500 年等6 种情况，雨峰系数设为0.17［9］，降雨历时为120 min。参考《南岸区城市内涝治理系统化实施方案》，重庆市南岸区暴雨强度公式为式（1），设计降雨过程线如图2所示。

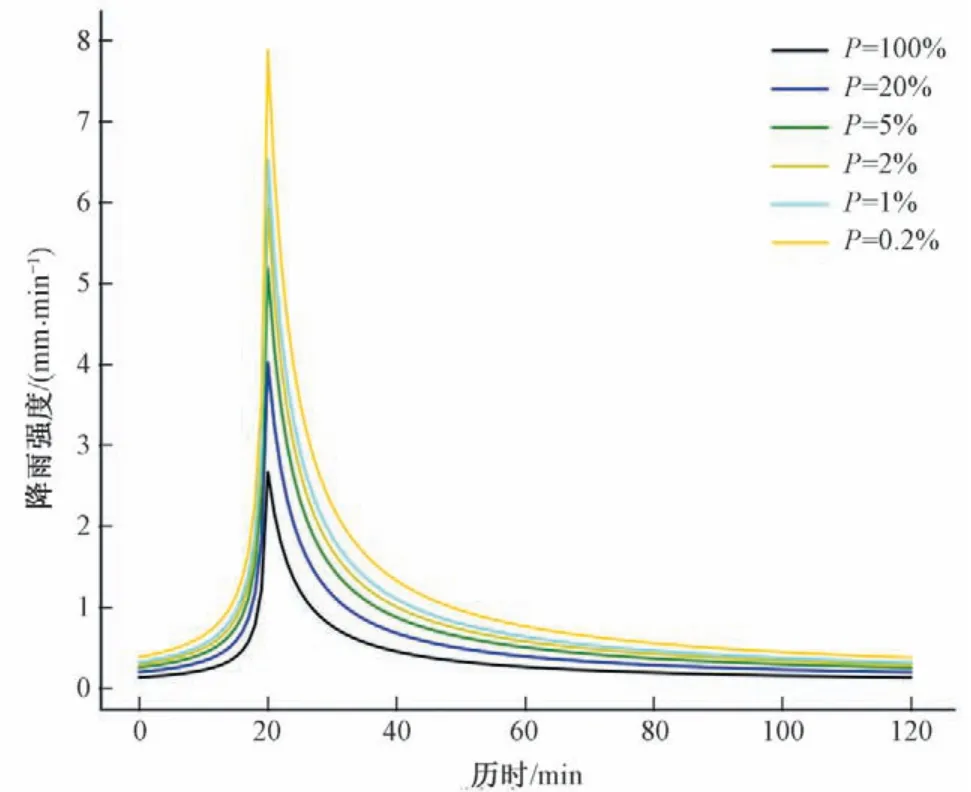
图2 设计降雨过程线Fig.2 Designed rainfall hyetograph

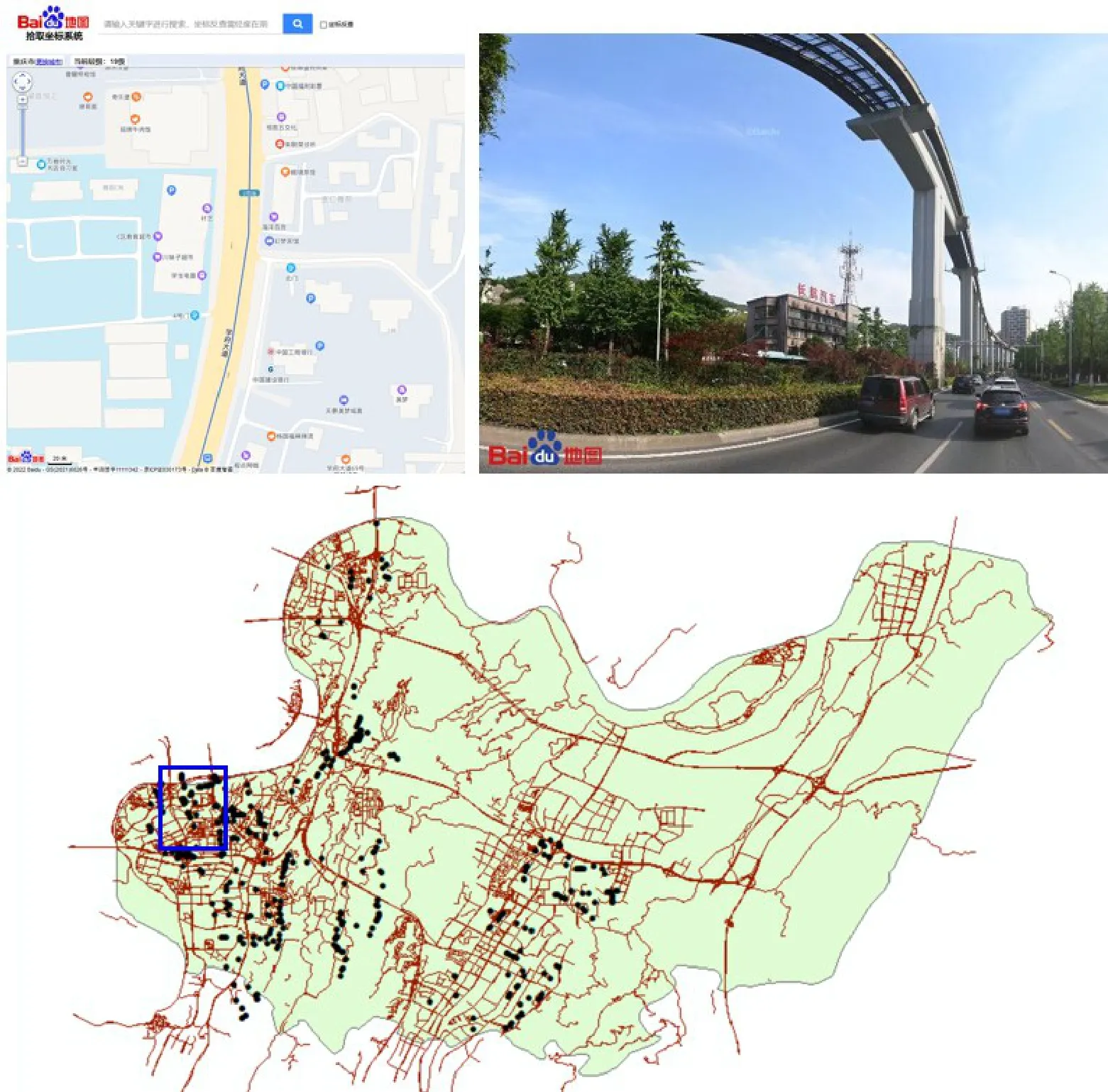
图3 研究区（蓝色方框）雨水检查井分布Fig.3 The distribution of extracted manholes in the study area

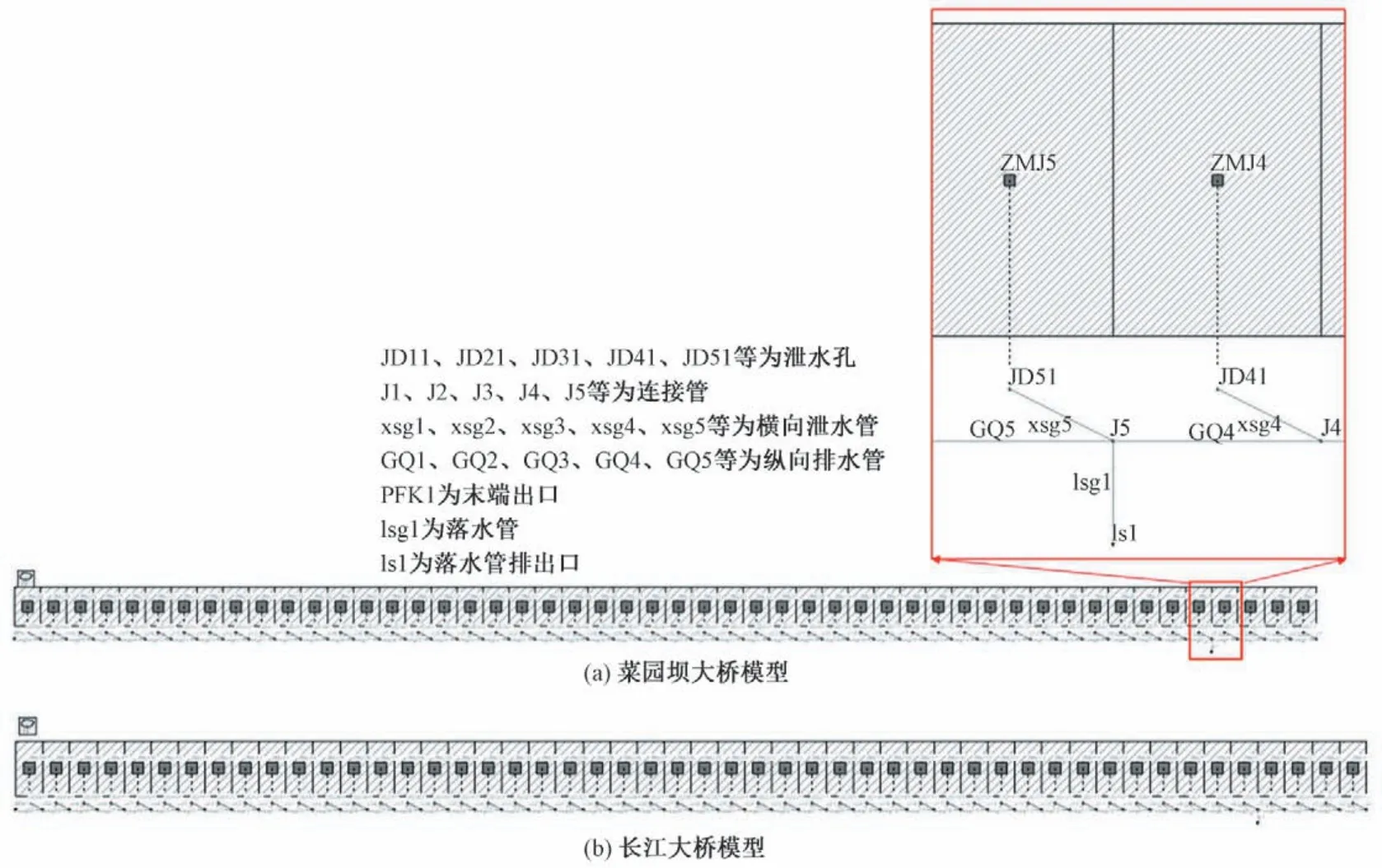
图4 基于SWMM的桥面径流模型Fig.4 Bridge deck runoff model based on SWMM

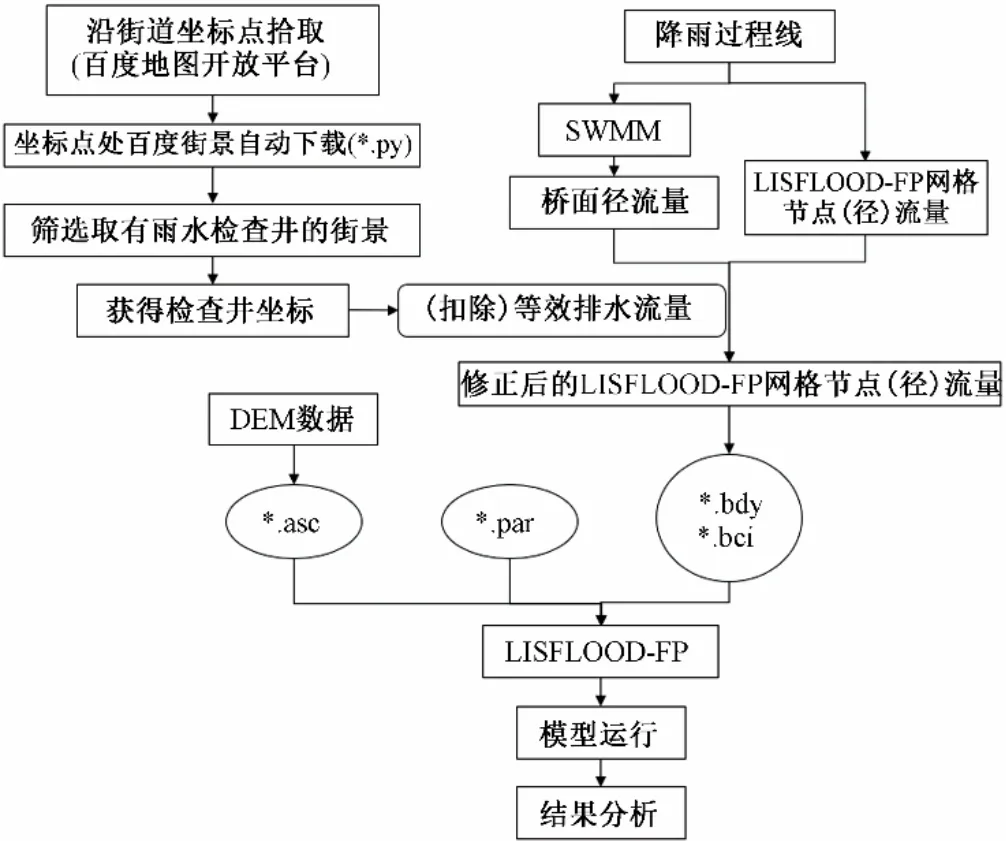
图5 模拟计算框架Fig.5 The modeling framework

式中：q为设计暴雨强度，L/（s·hm2）；P为设计暴雨重现期，a；t为降雨历时，min。

1.3 雨水检查井信息获取

利用百度地图开放平台提供的全景静态API 功能，开发基于Python 的道路全景批量自动下载和处理程序，对研究区内的雨水检查井进行识别和定位。主要步骤包括：首先，在百度地图开放平台提供的坐标拾取界面（https：//api.map.baidu.com/lbsapi/getpoint/index.html）对研究区所有道路坐标点进行提取；然后，将提取的所有坐标作为输入，运行所编写的基于全景静态API 接口的Python 程序，批量下载指定坐标位置的街道全景照片；最后，通过对所下载的照片进行筛选，从而确定检查井的分布。

1.4 LISFLOOD-FP模型

LISFLOOD-FP 模型［10-13］是由英国布里斯托大学开发的二维洪水动力模型，以栅格化网格为计算单元，可实现基于浅水方程简化形式的一维河道水力和二维水动力过程模拟。LISFLOOD-FP 模型针对不同应用场景提供了多种模型求解器以及边界条件输入方式。构建城市区域洪水漫流模型，所需准备的数据文件主要包括地形（*.asc）、边界条件（*.bci和*.bdy）和模型运行文件（*.par）。在本研究中，对于二维地表漫流计算，采用基于完整浅水方程求解的FV1求解器。

在模型中采用雨水井等效排水法［6，14］，将管网排水概化为通过雨水检查井所在点排出，根据地区管网设计标准结合堰流公式对检查井入流量进行确定，而后将其作为点源边界条件在模型中进行设置［15］。

1.5 SWMM模型

随着城市立体交通的日趋成熟，桥梁作为其重要组成部分，往往建设在区域连接的关键节点，一旦因降雨集中或桥梁排水系统运行不畅导致桥面积水，不仅会直接影响桥面行车安全，甚至会以点带面加重局部内涝程度。而在以往的城市内涝研究中，对桥梁排水系统和桥面径流关注较少，例如，刘非等［16］利用InfoWorks ICM 对武汉长江隧道内暴雨积水过程进行了模拟分析，但未考虑隧道口附近沙湖大桥桥面雨水径流的影响。

为考察研究区北面两座桥梁桥面径流对局部内涝的影响，利用SWMM 模型进行桥面径流计算，桥面径流量模拟结果作为边界条件输入LISFLOOD-FP 模型中进行二维洪水地表漫流计算。

菜园坝大桥和长江大桥是连接渝中区与南岸区的过江通道，位于长江水道之上。菜园坝大桥线路全长7 km，主桥长约800 m，桥面为双向六车道快速路（宽度约30.5 m）。长江大桥全长1.1 km，桥面为双向八车道（宽度约40 m）。桥面横向泄水管按照20 m间距布设考虑，桥面径流系数取为0.95［17，18］。

1.6 降雨径流计算

暴雨作为内涝产生的根本原因，其对内涝积水的影响因素除雨型、降雨强度、降雨历时外，还受到地形及用地类型等的作用。在传统的半分布耦合模式［19］中，降雨作为输入条件被关联到每个汇水区，分别计算产流，而后进入到管网系统，若管网排水不畅产生节点溢流，则通过检查井与地表进行水量交换。这种概化方式虽有一定水文学理论依据，但忽略了径流在进入管网系统前的地表漫流过程，与实际汇流仍有差别。在Info-Works ICM 等软件中，模型提供了与实际过程更符合的直接降雨法，但该方法缺点是计算较为耗时，需采用较为高效的模型算法［20］，但总体而言相关研究较少。

研究区采用直接降雨法进行径流模拟，即基于栅格的径流模拟方法，将整个研究区按地形栅格划分结构计算单元，每个计算单元包含高程、粗糙系数、渗透参数、不透水区百分比和洼地深度等信息，地表产流由每个单元独立产生［21］。每个计算单元按用地类型或地表覆盖物种类划分为透水区和不透水区，分别进行产流计算。对不透水区，径流量等于降雨强度，而在透水区，径流量等于降雨强度减去入渗损失。最终，所有计算单元所得产流均作为边界条件输入LISFLOOD-FP 模型进行二维洪水地表漫流计算。

式中：Qm为第m个计算单元的产流量，m3/s；i为降雨强度，mm/min；f为下渗量，mm/h；Sm为第m个计算单元的面积，m2。

采用Horton模型对透水区入渗率进行估算。基本方程为：

式中：ft为t时刻的下渗率，mm/h；fc为稳定下渗率，mm/h；f0为土壤初始下渗率，mm/h；k为衰减系数，与土壤的物理性质有关，1/h；t为时间，h。参数取值参考SWMM模型手册。

2 模拟方法验证

2.1 水量平衡分析

为考察将直接降雨法所得径流量结果作为边界条件驱动LISFLOOD-FP 模型进行洪水计算的可行性和准确性，通过对理想算例进行水量平衡分析作为验证。算例为长宽均为100 m的方形区域，以10 m 网格进行划分。建立同区域的SWMM 模型，同样降雨作为输入，对比验证公式法计算的径流量精确值、SWMM模型模拟的径流量、LISFLOOD-FP模型模拟所得洪水量三者的吻合程度。模型时间为4 h。降雨输入和结果对比如图6 所示。图6（b）中LISFLOOD-FP 模型模拟的地表洪水量与公式法计算所得径流量精确值、SWMM 模型模拟所得径流量均吻合良好。计算区域初始和最终时刻的水位分布如图7所示。

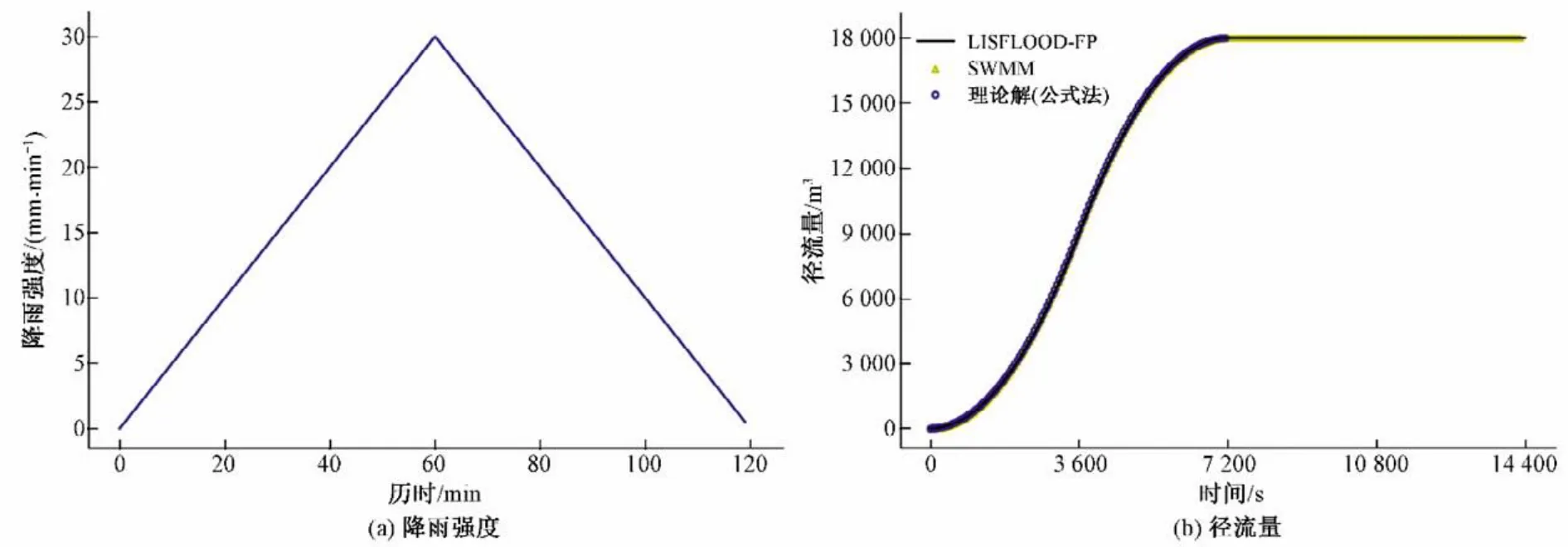
图6 理想算例降雨输入和不同径流量模拟方式所得结果对比Fig.6 The rainfall input and comparison of different runoff calculation methods

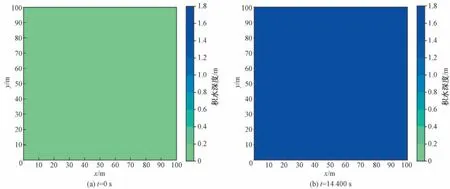
图7 初始和最终时刻区域水位分布Fig.7 Water surface elevation at the initial and final time step using LISFLOOD-FP model

2.2 易涝点对比

利用2022 年7 月30 日实测场次降雨对所提出的模拟方法进行验证，降雨数据来源为重庆交通大学山地城市降雨和内涝风险监测系统，降雨测量装置安装在校园内港航楼楼顶［如图8（a）］。图9 为模拟所得内涝点与文献［22，23］中所提到研究区典型易涝点对比，与实际监测记录位置基本一致。表1 和表2为该场降雨期间易涝点位置的峰值积水面积和积水深度模拟值与实测值对比，可见所提出的模拟方法在确定积水面积上准确度较高，而对积水深度的高精度模拟存在不足，以及易涝点D的积水范围和积水深度的模拟值与实测值相对误差较大，可能是由于地形精度较低导致。

表1 峰值积水范围模拟值与实测值对比Tab.1 Comparison of the peak flood area between the simulated and measured

表2 峰值积水深度模拟值与实测值对比Tab.2 Comparison of the peak flood depth between the simulated and measured

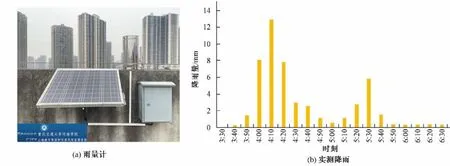
图8 雨量计与实测降雨Fig.8 Rain gauge and the measured rain process

图9 模拟所得内涝点与实际易涝点对比（易涝点数据来源于文献［22，23］）Fig.9 Comparison of simulated flood-prone points and the reported ones

3 结果及讨论

3.1 积水特征变化

将不同重现期的降雨过程线应用直接降雨法所得径流量作为边界条件输入LISFLOOD-FP 模型，得到研究区内涝积水变化过程。积水量可以表征内涝区域的总体积水情况，对各重现期降雨条件下研究区的积水量和积水面积随时间变化进行统计，如图10 所示。总体而言，积水面积变化规律与对应的降雨过程线变化较为相似，重现期越大，则同时刻的积水面积越大。积水面积峰值出现的时间与降雨重现期大小无关，但相比雨峰有滞后；积水面积在降雨结束（7 200 s）后出现较快下降，并最终保持稳定。随着重现期的增加，积水量也在相应的增加。通过对比积水面积变化，区域积水量增长速率最快的时刻与积水面积达到峰值的时刻基本一致，均在约1 800 s 时，晚于雨峰出现时间。在积水面积达到峰值并开始逐渐下降阶段，积水量仍在增加，这表明积水范围虽在快速缩小，但陡坡路段可能面临较大洪水流速，对行人，尤其是儿童和老年人仍存在较大威胁，需注意避开水流较急的危险路段。

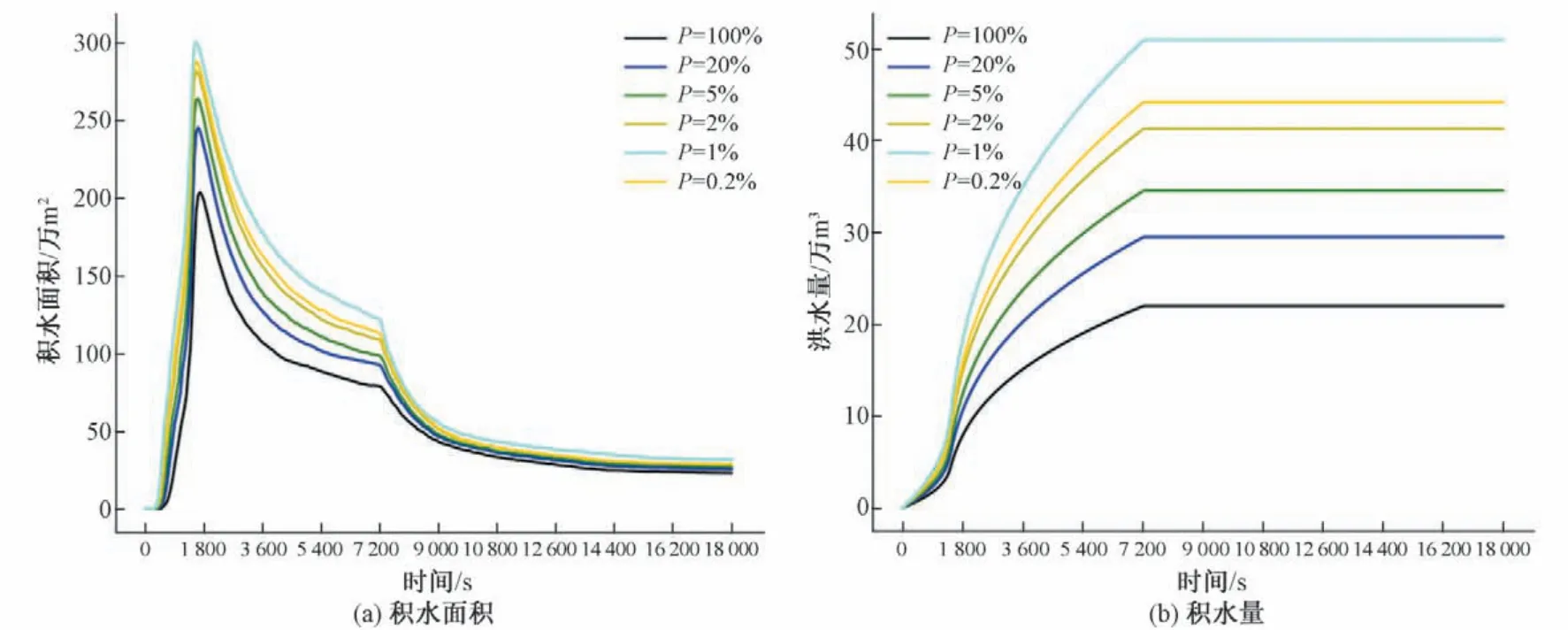
图10 积水面积和积水量随时间变化Fig.10 Time-series variation of the flood area and flood volume

3.2 内涝积水分布

内涝积水分布图可用于排查易涝点和分析积水原因，绘制出研究区不同降雨重现期下最大积水时刻的积水分布图，如图11所示。随着降雨重现期的增加，积水点的数量和范围均在增加，但易涝点（降雨重现期较小时即发生较严重积水的地段）的空间位置变化不大，在研究区最北端、中部、东南部、西南部均存在，只是当重现期增大后，原先零散的易涝点有互相连接成片的趋势。通过查看该区域地形［图1（b）］，可知内涝点基本分布在地形较为低洼处，比如研究区最北端连接长江大桥的地段，该区域的积水是由与之相邻区域的洪水汇集而成。由于所采用地形数据精度有限，不能十分精准地刻画该区域城市建筑、道路等，因此该积水分布可作为内涝点快速分析的参考。在未来将通过无人机探测等手段获取高分辨率的数字地表模型（DSM）来构建更高精度的内涝计算模型，提供更加准确的积水风险信息。

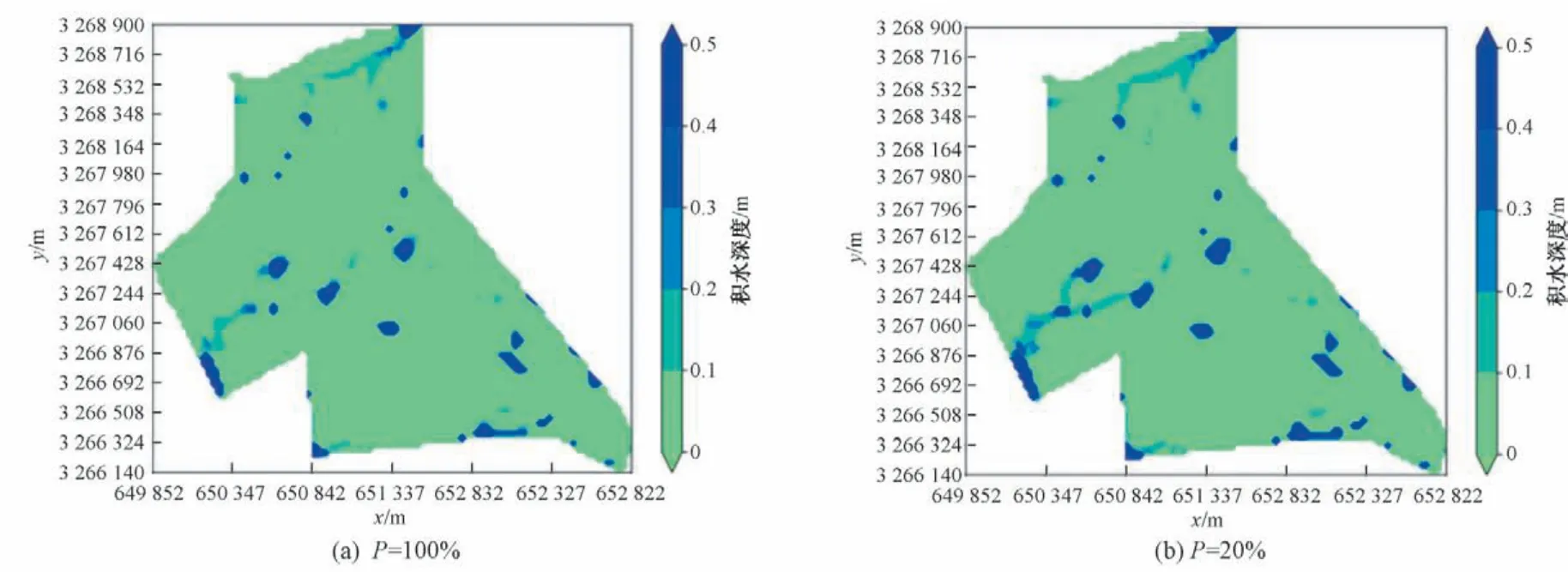
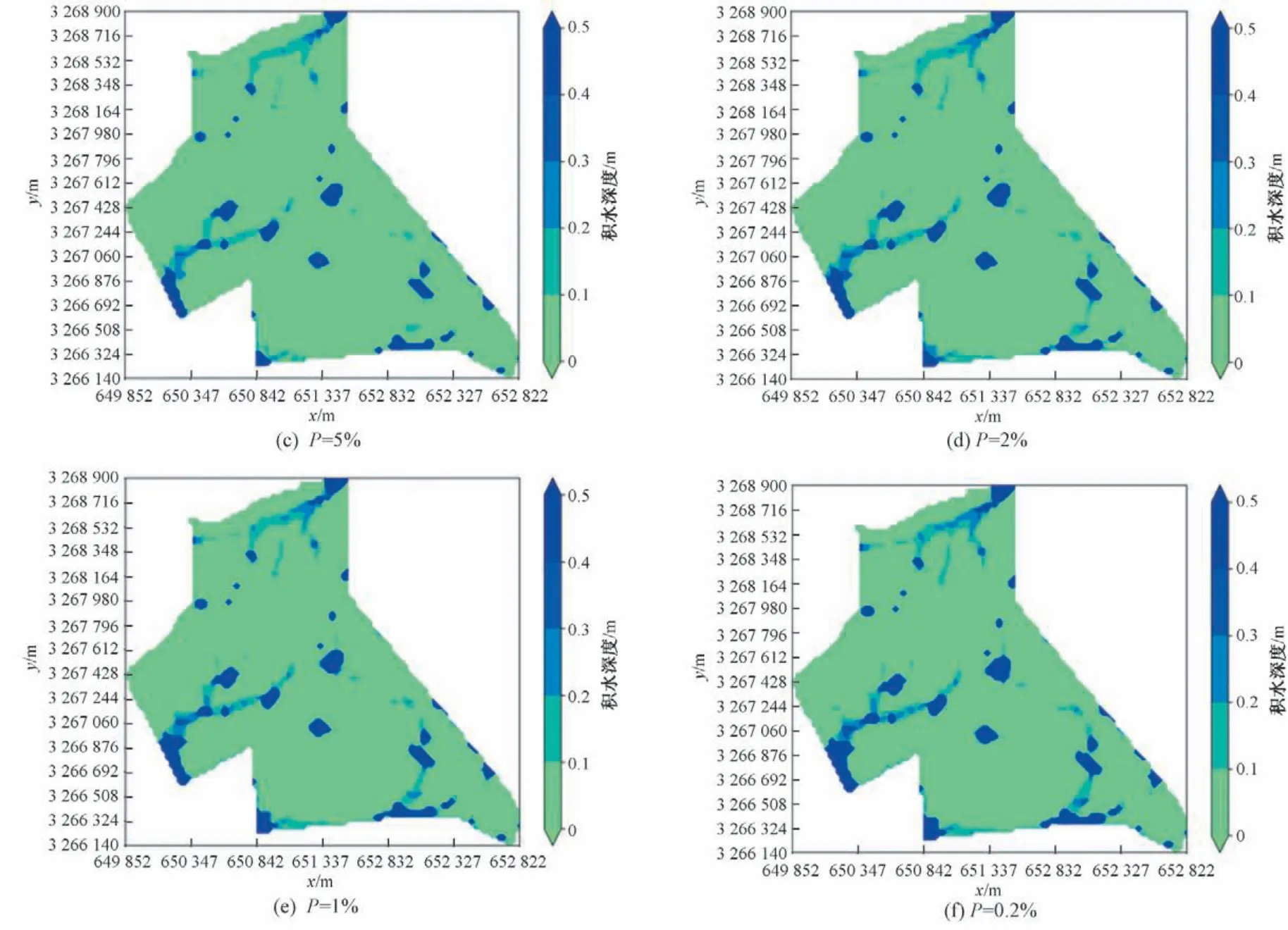
图11 研究区域不同重现期下最大积水分布（t=6 120 s时刻积水分布）Fig.11 Peak flood distribution of the study area under different rainfall scenarios

由于研究区北面长江大桥连接处地势较低，易形成较高积水风险，将SWMM 计算所得桥面径流量（P=0.2%）作为边界条件输入LISFLOOD-FP 模型，所得最大积水时刻的积水分布如图12 所示。与未加入桥面情况［图11（f）］相比，此时研究区北部的积水范围有明显增加，且主要集中在与菜园坝大桥连接处地段，与长江大桥连接处的积水程度也略有增加。因此，在针对地形变化复杂的山地城市内涝风险排查分析中，应对桥梁排水系统的运行情况以及桥面径流的影响纳入考虑。

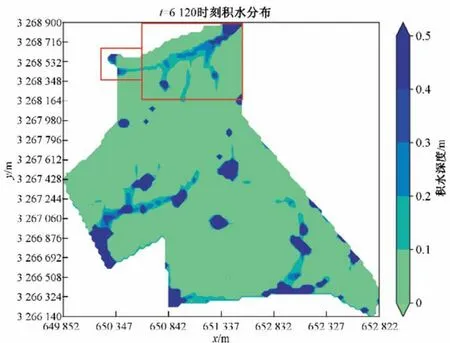
图12 最大积水时刻研究区积水分布（P=0.2%）Fig.12 Peak flood distribution of the study area

3.3 模型计算效率

山地城市由于地形起伏变化大，降雨时空异质性明显，内涝的发生和发展往往较为迅速，对较大范围的雨洪风险点进行高效计算和识别是预防和减少灾害损失的重要前提。研究区LISFLOOD-FP 网格规模为92×99个，网格尺寸为30 m×30 m，模型时间为5 h，模拟时间步长设置为1 s。在普通个人电脑（配置：8 核；Intel Core i7-1065G7 CPU、主频1.30 GHz）上，耗时约36 s，而在高性能计算机（配置：48 核；Intel Xeon 8275、主频3.0 GHz）上仅需不到3 s 即可完成计算，耗时均为同工况测试5 次平均结果。可见，应用该模拟方法可实现对大区域内涝风险进行快速诊断识别。

4 结 论

以山地城市重庆某城区为研究区域，提出了无管勘资料条件下内涝高效模拟计算方法，采用理想算例和历史降雨进行了验证，并对区域内不同暴雨情景下的内涝积水进行了模拟分析。在无管勘资料区域，利用百度地图开放平台全景静态API功能可对区域内的道路检查井进行有效确定。基于LISFLOOD-FP，采用雨水井等效排水法和直接降雨法，可实现对较大区域范围雨洪的高效计算和对易涝点进行识别。

积水面积和积水量的变化均与降雨变化较为相似，重现期越大，则同时刻的积水面积和积水量越大；积水量增长速率最快的时刻与积水面积达到峰值的时刻基本一致，晚于雨峰出现时间。在积水面积下降阶段，积水量仍在增加，陡坡路段可能面临较大洪水流速，对行动不便的群体仍存在较大威胁，需注意防范。对于地形起伏变化大的山地城市区域，桥面径流可能会加重局部内涝的程度，应予以关注。

所提出的模拟计算方法可为类似无管勘资料区域内涝风险高效评估提供技术参考，对LISFLOOD-FP 模型在国内的使用提供借鉴。