基于指数核函数高斯过程回归的短期径流预测研究

何中政，方 丽，刘 万，迟英凡，王永强，付吉斯，熊 斌

（1. 南昌大学工程建设学院，江西 南昌 330031； 2. 长江水利委员会长江科学院，湖北 武汉 4 30010；3. 南昌大学 鄱阳湖环境与资源利用教育部重点实验室，江西 南昌 330031）

0 引 言

流域径流过程受众多因素的相互作用与影响，使得径流时间序列表现出复杂的非线性特性［1］，具有显著的非平稳、高维度和模糊性等复杂特征［2，3］，研究预测精度高和稳定性好的径流预测模型仍是当前水文水资源研究领域热点问题之一。而目前水文预测方法主要可分为过程（机理）驱动和数据驱动模型两大类：过程驱动模型以水文过程的物理机制或规律为基础［4］，需要大量且可靠的水文数据来建立模型，从而进行流域径流模拟或预测，但由于水文模型对水循环过程的简化处理，往往难以精准刻画非线性的径流过程，且由于部分水文数据资料缺失或可靠性差等因素影响，过程驱动模型在实际径流预报中存在局限性［5］；而随着计算机硬件、软件和理论技术的发展，数据驱动模型依托统计学或其他人工智能技术，无需考虑水文过程物理机制［6］，通过对时间序列进行分析从而建立对预测对象和预测因子间复杂非线性关系刻画更为完备的模型，使得数据驱动模型在水文数据资料缺少或复杂非线性的径流过程将具有更好的适用性［2］。近年来，学者们将多种常见的人工智能模型引入到水文预测中，如前馈式神经网络［7］（Back-Propagation neural network，BP）、多元线性回归［8］（Multiple Linear Regression，MLR）、支持向量机［9］（Support Vector Machine，SVM）等，相关研究均取得了较好的效果［10］，如何应用人工智能技术开展流域径流预测已经成为未来发展的重要研究方向之一［11］。

高斯过程回归（Gaussian Process Regression，GPR）作为一种新型的机器学习方法，采用高斯过程对先验数据进行回归分析，以统计学理论为基础，在处理高维、非线性、小样本等复杂的回归问题时都具有很强的泛化能力，因而在各类研究领域得到应用［12］。黄亚等人［3］采用GPR 模型在广西天峨水文站进行短期径流预测；孙斌等人［13］采用GPR 模型在进行短期风速预测；李成宇［14］采用GPR 模型进行了土石坝沉降预测研究；周靖楠等人［15］采用GPR 模型与MI-KPCA 结合在北汝河进行中长期径流预测。刘龙龙等人［16］采用GPR 模型与蜻蜓算法结合对居民社区时用水量动态实时区间预测。GPR 模型已在非线性回归分析问题中得到成功应用，GPR 回归分析能力不仅取决于模型参数，还受核函数影响，但目前核函数的影响还未得到进一步研究。Scholkopf 和Smola［17］指出支持向量机和高斯过程两种算法的核函数是等价的，并提出几种高斯过程中可选择的核函数类型。因此，本文分析了不同核函数作用下GPR 预测模型效果，并提出了一种基于指数核函数GPR 的流域短期径流预测模型，以江西省赣江流域吉安水文站径流过程为对象例开展实例分析。

1 研究方法

1.1 高斯过程回归预测模型基本原理

高斯过程（Gaussian Process，GP）是概率论和数理统计中随机过程的一种，是一系列服从正态分布的随机变量的组合。GP继承了正态分布的诸多性质，其特征主要由数学期望和协方差函数决定。GPR 则是对数据进行回归分析，来建立服从GP 先验信息的非参数模型［18］。假设一个含有n对相互独立观测数据的学习样本{，y}，其中是由n个输入向量组成的输入集，而y={y1，y2，…，yn}是由n个相对应的一维输出组成的输出集。那么GP 的均值μ(x)和方差k(x，x′)可由下式确定：

式中：x，x′代表样本中任意随机变量，E代表数学期望。

因此GP可定义为：

而在实际应用中，通常会进行数据预处理使得均值函数为0，故GP即也表示为：

对于实际工程中的回归问题，还应考虑输出y受噪声影响：

式中：y是受到噪声污染的观测值，f为函数值，x为输入向量，噪声ε服从均值为0、方差为σ2n的高斯分布。

从而可以推求得到y的先验分布，见公式（6）；以及y和f(x*)的联合先验分布，见公式（7）。

式中：x*为测试输入向量，I是n维单位矩阵，是n×n阶的GP 协方差矩阵，是输入集与测试输入向量x*之间的n× 1阶协方差矩阵，K(x*，)同理可知，k(x*，x*)为x*自身的协方差。

由此可知预测值f(x*)的后验分布：

其中：

1.2 高斯过程回归的核函数与超参数优化

GPR 使用GR 作为先验，其训练结果与预先设定的核函数有关。在随机样本均值为0 的前提下，核函数就与协方差函数的实际意义相近，可进行样本间相关性的描述。不同核函数作用下的高斯过程回归特征各不相同，高斯过程模型常用的核函数主要有以下几种：

（1）径向基核函数：

式中：r=‖X1-X2‖，σ为超参数，表征了学习样本间的相似度。径向基核函数也被称为高斯核，常被应用于SVM和GPR等各类机器学习算法中，参数简单，但在处理样本数量大或特征多时效果一般。

（2）二次有理核函数：

式中：α，l为超参数。二次有理核函数可以理解为是无穷个径向基核函数的线性叠加，当α→∞时，二次有理核函数等价于σ=l的径向基核函数。与径向基核函数相比，更为省时，作用域广，但是对参数十分敏感。

（3）马顿核函数：

式中：l，ν为超参数，Kν为修正贝塞尔函数。当ν→∞时，相当于以l为特征尺度的径向基核函数。

（4）指数核函数：

指数核函数是马顿核在ν= 0.5的特殊形式，这样的变动减少对参数的依赖性降低，使得模型的训练学习难度大大降低，适用情景相对狭窄。

而核函数中的超参数一般可依据极大似然法，建立基于学习样本条件概率的对数似然函数，见式（15）；然后可通过非线性规划方法或群智能搜索方法寻找出超参数的近似最优解。

1.3 预报因子筛选

由于径流预测往往是采用输入多个预测因子对预测量进行输出，研究采用多重相关系数来筛选预报因子。多重相关系数是测量单个因变量与其他多个自变量之间线性相关程度的指标。多重相关系数无法直接计算，可采用预测量y和其他多个预测因子x1，x2，…，xk线性组合的简单相关系数进行测算。

首先，根据预测量y和其他多个预测因子x1，x2，…，xk进行回归，建立如式（16）的回归方程，然后进一步计算简单相关系数，即为预测量y和多个预测因子x1，x2，…，xk之间的多重相关系数R。

式中：β0，β1，β2，…，βk为回归系数。

2 实例研究

2.1 研究区域与资料概况

赣江是江西省内第一大河流，地理位置为113.58°～116.63°E，24.52°～28.75°N。其发源于赣闽边界武夷山西麓，主河道长约823 km，干支流自南向北贯穿整个江西省，地貌多以山地、丘陵为主，丰水期为3-8月，枯水期为9月-次年2月。

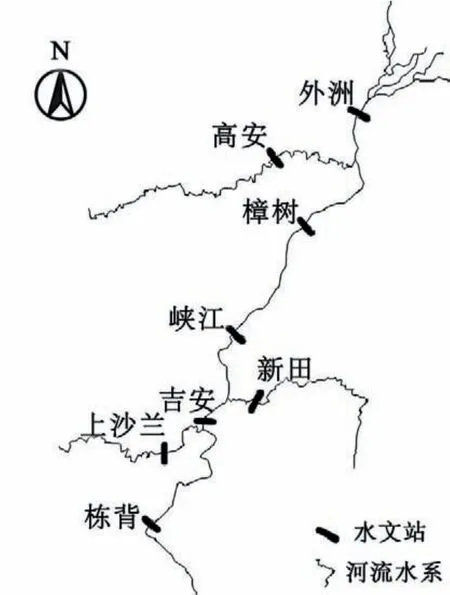
图1 赣江中下游控制断面分布示意图Fig.1 Distribution diagram of control section in the middle and lower reaches of Ganjiang River

研究选取了赣江中游栋背、吉安关键断面开展实例分析。栋背站位于江西省万安县栋背村，控制流域面积约4.02 万km²；吉安站是赣江中游主要控制站，控制流域面积约5.62 万km²；栋背站到吉安站的时滞约为18～24 h，栋背站对吉安站的流量过程有较大的影响。研究收集整理了两个水文站点从2010 年1月1 日0∶00 至2018 年4 月14 日18∶00 的实测径流数据，时段间隔为6 h，共计20 000 个数据。

2.2 基于高斯过程回归的径流预测流程

依托项目研究收集得到的数据资料，开展基于GPR 模型的径流预测研究。具体实施步骤为：① 整编收集得到的径流数据资料，将前80%作为预测模型训练期，后20%作为预测模型检验期；②根据率定期径流资料，计算预报因子-预测量的多重相关系数，开展相关性分析，从而选定预报因子；③选取评价指标，便于直观表现模型的预测效果；④采用GPR 对预报因子和预报变量进行建模，用训练期资料进行参数率定；⑤将训练好的GPR模型用于检验期的径流预报，检验模型预报效果。

2.3 评价指标选取

为评价预测结果的综合表现，选取了均方根误差（Root Mean Squared Error，RMSE）、平均绝对误差（Mean Absolute Error，MAE）、确定性系数（Deterministic coefficient，DC）和合格率（Qualified Rate，QR）评价指标，具体计算公式如下：

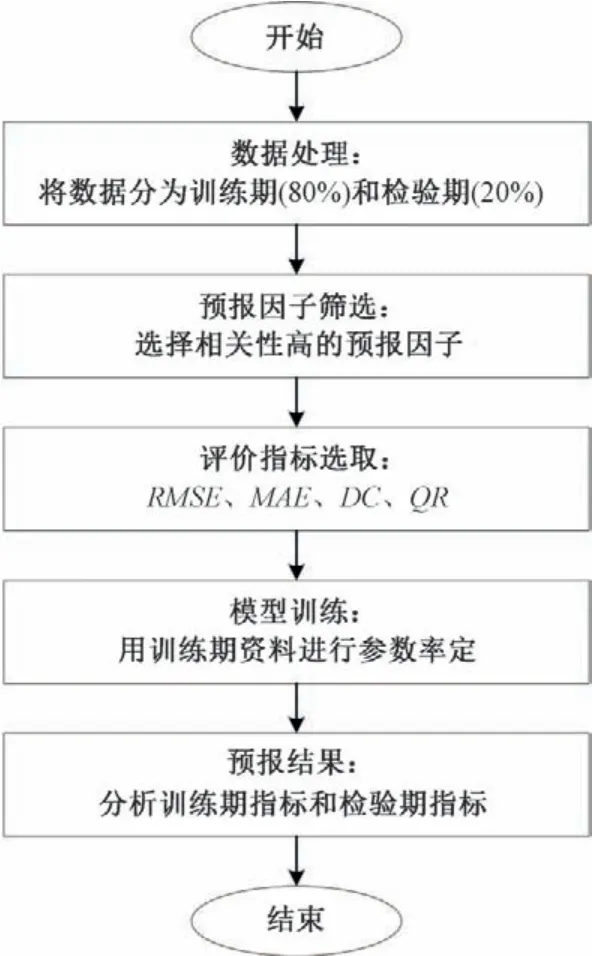
图2 基于高斯过程回归的径流预测流程图Fig.2 Flow chart of runoff prediction based on Gaussian process regression

式中：Si为模拟值；Oi为实测值；为实测值的均值；k为样本中相对误差小于20%的样本个数；n为测试样本个数。评价指标中，RMSE和MAE取值范围为(0，∞)，其值越小表明模型预测误差越小；DC取值范围为[0，1]，其值越大表明预测值和真实值的相关性越大；QR取值范围为[0，100%]，其值越大表明模型预测精度越高。

2.4 预测因子筛选

建立短期径流预测模型首先需要筛选预测因子，记T为当前时段，OT和IT分别表示本站点和上游站点T时段径流量。采用IBM SPSS Statistics 26.0 软件开展见2.3 小节中的多重相关系数分析，多重相关性分析结果如表1和表2所示。

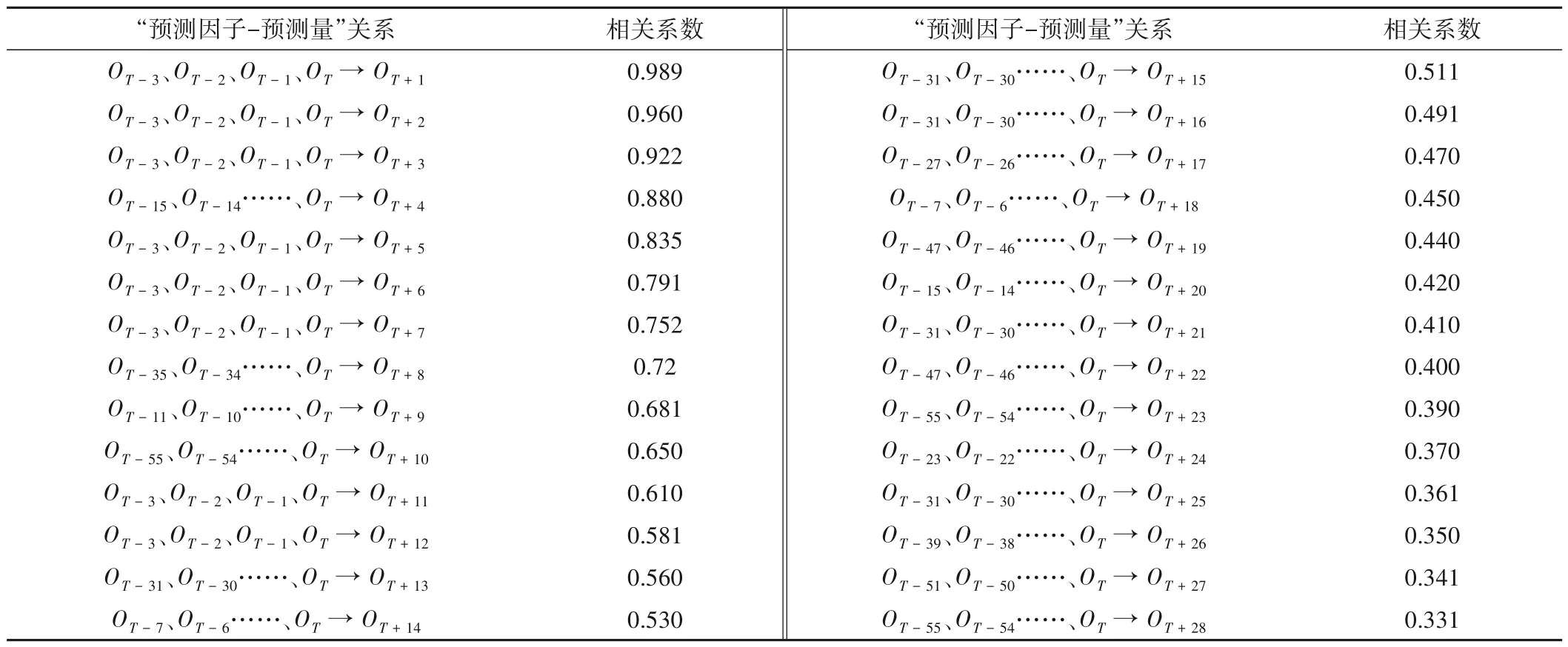
表1 仅考虑吉安站的多重相关性分析结果Tab.1 The multiple correlation analysis results of Ji'an Station

表2 考虑栋背站和吉安站的多重相关性分析结果Tab.2 The multiple correlation analysis results of Dongbei station and Ji'an station

表1 和表2 仅列出了与吉安径流多重相关性系数最大，且预测因子时段最短的组合。对比表1 和表2 可知，增加栋背径流信息对“预测因子—预测量”复相关性系数增益较为明显，因此研究选择表2中预测因子开展短期径流预测。

2.5 径流预测实例分析

采用数据留出法［19］进行评估，将样本数据的前80%作为模型训练样本，后20%作为模型检验样本，即训练期为2010 年1月1 日0∶00 至2016 年11 月19 日18∶00 的实测径流数据，时段间隔为6 h；检验期为2016 年11 月19 日18：00 至2018 年4 月14日的实测径流数据，时段间隔为6 h。根据表2 中的预测因子，建立28 个基于GPR 的短期径流预测模型，分别对面临T+1～T+28 时段的吉安径流进行预测。为分析不同核函数对GPR 短期径流预测模型的作用效果，研究分别选用了有理二次、径向基、马顿和指数核函数建立不同的GPR 短期径流预测模型，还加入了MLR、回归树（Regression Tree，RT）、SVM、BP 等模型方法的预测结果作为对比。以上模型的训练以及检验均采用MATLAB R2020b 进行处理，GPR、MLR、RT 和SVM 模型训练基于Regression Learner 模块，BP 模型训练基于采用的Neural Net Fitting模块。

图3 给出了吉安站不同模型短期径流预测在检验期的结果，见T+1～T+27 时段4 种评价指标的热力图。4 张热力图均为颜色越深，检验期预测效果越差。相关实验结果表明：①从4种指标综合来看，研究建立的4 种GPR 模型和RT 模型均优于MLR、SVM、BP 模型，在DC指标上差异最为显著，4 种GPR 模型和RT 模型的DC均在0.9以上，而MLR、SVM、BP 模型DC前2个时段大于0.9，随预见期增长DC锐减至不足0.4；②从4 种GPR模型对比来看，有理二次、指数GPR 优于径向基和马顿GPR，结合核函数表达式（11）～（14）来看，径向基和马顿核函数明显比有理二次、指数核函数更复杂，这表明复杂的核函数形式不一定能提升GPR 模型非线性回归分析能力；③随着预测期的增加，MLR、SVM、BP 模型的4种评价指标均呈现劣化的趋势，4种GPR 模型和RT 模评价指标有略微波动，但整体较为稳定；④综合各项评价指标来看，有理二次、指数GPR 模型结果最为突出，而指数GPR 模型的RMSE、MAE、QR明显优于有理二次GPR，指数GPR 模型在28个时段的QR中仅有1处合格率不足100%，明显少于有理二次GPR 的22 处。综上所述，本文提出的指数GPR在吉安站短期径流预测中显著优于其他6种模型方法。

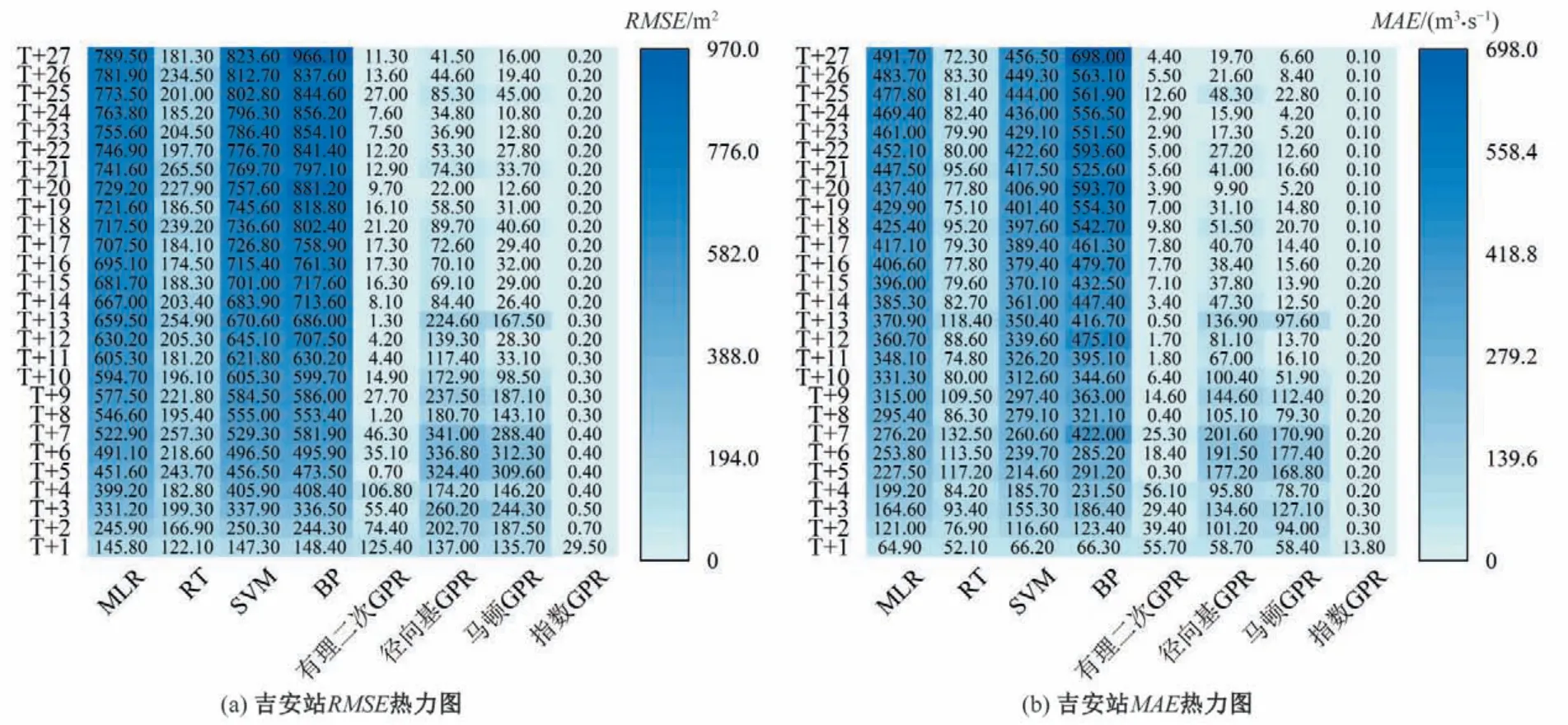
图3 吉安站检验期各模型评价指标热力图Fig.3 Heat map of each model evaluation index for the testing period at Ji'an Station

图4和表3分别给出了吉安站不同模型短期径流预测T+28时段的预测结果和4 种评价指标统计结果，7 种模型方法在训练期和检验期4 项评价指标变化不大。此外，研究发现4 种GPR 模型检验期4项评价指标在T+1到T+9时段逐渐劣化，4项评价指标随后在T+10到T+28时段变好并趋于稳定。结合多重相关性分析结果，可知T+10 时段以后预测模型输入信息激增，有助于数据驱动的GPR 模型开展回归预测分析。这也说明应用多重相关性系数分析筛选出的“预测因子—预测量”关系，并不能完全反映自身和上游站点径流的非线性关系。

表3 吉安站T+28时段训练期和检验期结果评价指标Tab.3 Evaluation indexes for the results of the training and testing period of the T+28 period at Ji'an Station

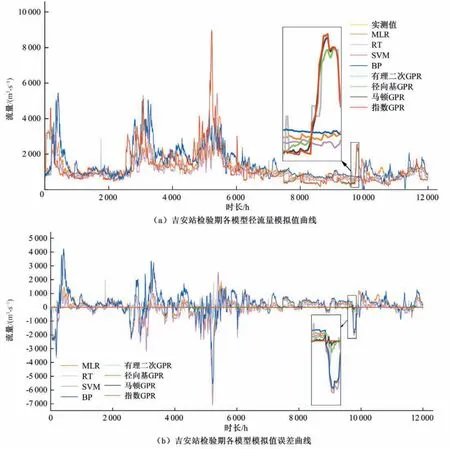
图4 吉安站检验期T+28时段预测结果Fig.4 Forecast results for the T+28 period of the testing period at Ji'an Station

3 结 论

（1）以赣江流域吉安水文站为对象的预测步长为6 h 预见期为7 d 的实例分析为例，应用不同核函数的GPR 模型预测结果表现存在明显差异，不同方法预测表现由好到差分别为指数GPR、有理二次GPR、RT、马顿GPR、径向基GPR、SVM、MLR、BP。指数GPR 预测效果最好，28 个时段的DC和QR均分别接近1和100%。

（2）从4 种GPR 模型对比来看，径向基和马顿核函数表达式比有理二次、指数核函数更复杂，但预测结果不如有理二次、指数核函数的GPR 模型，说明复杂的核函数形式不一定能提升GPR模型非线性回归分析能力。

（3）4 种GPR 模型检验期预测精度在T+1 到T+9 时段逐渐降低，但在T+10 到T+28 时段，随预测模型输入因子信息激增，预测精度提高并趋于稳定。

（4）多重相关性系数分析筛选出的“预测因子—预测量”关系，主要依据线性关系，并不能反映自身预测量和上游站点预测因子的非线性关系。在未来的研究中，需探究能够精准描述预测因子与预测量复杂非线性关系的分析方法，从而更为准确的筛选预测因子。