基于全耦合的地表水土壤水运动与溶质运移数值模拟

鲁舒心，万愉快，孙伯颜，农睿，朱磊

（1.宁夏大学土木与水利工程学院，银川 750021；2.宁夏回族自治区黄河水联网数字治水重点实验室，银川 750021）

0 引 言

降雨径流从坡面流下的过程中会发生下渗[1]，与此同时，溶质也会随着水分运动在地表与土壤间进行迁移转化[2]。由水分运动驱动的溶质迁移往往是坡地养分流失的主要原因，不仅降低了耕地肥力造成经济损失，还会导致农业面源污染，产生河湖等地表地下水体污染和富营养化的风险[3,4]。在水资源短缺，水污染尤其是面源污染问题日益严峻的当下，研究地表水土壤水水分运动与溶质迁移规律，对防治和解决水资源与水生态问题具有重要意义。

目前，有关地表水土壤水运动与溶质运移过程的研究，大多是通过野外现场监测和室内模拟试验相结合的方式进行。野外监测能够通过现场试验直观地理解水分和溶质迁移过程[5]，获取较为真实的数据资料，为数值模型的开发奠定基础。室内试验的数据采集和监测更加方便准确，可以人为控制实验条件并具有可重复性。近年来，随着计算性能的提高和数值求解算法的改进，构建数值模拟模型成为定量化研究地表水土壤水与溶质迁移的一个重要手段[6]。相比于野外监测和室内试验，数值模拟克服了试验过程人为因素多、监测手段受限等不足，不仅可以获取整个研究区内水分和溶质浓度的空间分布状态以及指定位置处的连续变化过程[7]，还可以高效地改变水力与介质参数和边界条件，对不同场景中的水分和溶质运移做出预测和解析，已经被国内外众多学者广泛运用。

在应用数学模型方法对地表水与土壤水进行模拟研究时，以往的研究中常将两者分开单独进行模拟，忽略了两者间的相互作用[8]。而地表水土壤水耦合模拟则是从系统分析的角度考虑水分在地表和土壤两部分中的运移转化，选用一定的耦合方法对表述两者的圣维南方程和连续性方程进行耦合。根据耦合方法的不同，可以将地表水土壤水水分耦合模型分为松散耦合模型、顺序迭代耦合模型、完全耦合模型等三类[9,10]。松散耦合模型[11-13]通常先求解地表模块，再求解地下水流，两模块间利用交换通量进行连接。此方法虽然计算效率较高，但由于采用了过多简化计算，且未考虑土壤水对地表水的反馈作用，使其模拟精度较低并可能导致质量平衡错误[10]，难以表述地表和土壤存在强交互作用时的水分运动。顺序迭代耦合模型[14-16]通过将交换量作为源汇项，交替求解地表和地下模块，实现了土壤水与地表水的双向反馈，提高了模拟精度，但计算的复杂度增加，使得计算效率降低。完全耦合模型[1]则是用全局隐式格式将地表水土壤水方程进行统一离散并同步求解，能够同时解决饱和模块、非饱和模块和界面边界条件问题[17]，模拟精度得到进一步提高，但由于计算的复杂性，国内外研究较少。在水量耦合研究的基础上，加入溶质运移方程，从物理机制上对地表地下水分运动与溶质迁移进行模拟的全耦合模型研究则更鲜见。

国内外对地表地下水溶质耦合模型的研究多基于现有的商业软件及其二次开发，如GMS，MODFLOW，Hydrus-2d等软件及各软件中的模块组合以建立耦合模型：付强等[18]利用GMS-FEMWATER构建了河流与地下水水流溶质运移耦合模型，李跃鹏等[19]将GMS-Borehole模块和MODFLOW模型结合，用以模拟浅层地下水水流，通过Hydrus-2D，RT3D，MT3DMS模型，建立了饱和-非饱和带污染物联合模拟模型。陈志慧等[20]通过构建SWAT-MODFLOW-MT3DMS耦合模型对沙颍河流域地下地表水硝酸盐通量过程做出了定量解析。此外，一些学者提出的部分水文模型也开发了溶质耦合模拟功能，如将地表和地下水互为边界条件结合菲克定律进行溶质运移耦合的PAWS模型[21]；通过溶质梯度计算地表地下交界处溶质通量的WASH123D模型[22]；以及耦合了地表模型FLUXNoah、PIHM模型、生物地球化学模型（RT）的BioRT-Flux-PIHM模型等[23]。上述模型在求解溶质运移问题时往往将地下水和地表水单独处理，通过较为松散的结果将两者进行耦合，导致地表与地下水相互影响的区域计算结果会有较大的偏差，进而影响溶质运移的模拟精度。为提高交界处的水通量和溶质交换量的计算准确度，有学者提出了双层结点法[24,25]，与公共节点法[26]相比，双层结点法不依赖于两个系统间的水头连续性假设，而是通过达西流关系来描述地表与地下水体之间的交换量[27]，提供了更多的灵活性，在描述地表-地下界面处的水头连续性更为准确，计算效率更高[28]。

本文针对地表水土壤水水分运动与溶质运移完全耦合模型研究相对较少的现状，基于二维扩散波方程和传统的三维Richards方程，采用双层结点法进行耦合，使用二维和三维对流弥散方程分别描述地表水和土壤水中的溶质运移，根据地表水和土壤水中的溶质浓度与两者间的交换水量计算溶质的交换量，从而构建地表水土壤水水分运动与溶质运移全耦合模型。根据已发表文献中不同算例的实验结果，验证本研究所提出模型的合理性和准确性并分析降雨条件下地表水土壤水运动与溶质迁移规律。

1 全耦合模型的构建

1.1 地表水土壤水运动耦合模型

1.1.1 土壤水运动数学模型

使用经典的变饱和土壤水分运动方程(Richards方程)表述地下区域的土壤水分运动[1,29]：

式中：θs为土壤饱和含水率，cm3/cm3；Sw为饱和度，其值大小等于土壤体积含水率θ和θs的比值；ϕ为土壤水分负压，cm；Qs为地表以下的源汇项，s-1；Qos为土壤水地表水交换量，s-1；xi(i=1，2，3)为三维笛卡尔空间坐标，对于垂直截面的平面流动，x1=x表示水平坐标，x1=z表示垂直坐标，取向下为负；t表示时间，s；Kij为土壤饱和导水系数张量，cm/s；Krw为相对非饱和导水率。

1.1.2 地表水运动数学模型

采用二维扩散波方程描述地表径流运动[30]：

式中：h0为地上水面高程，cm；h0=z0+d0，z0是地表高程，cm；d0是地表水深，cm；Qo是地表水的源汇项，cm/s；kox和koy分别为x、y方向上的地表水力传导系数，cm/s。

1.1.3 地表水与土壤水运动的耦合

朱磊等[1]采用双层结点法对土壤水运动模型和地表水运动模型进行全耦合，并通过对比分析模型试验结果验证了该方法的合理性和可靠性，因此本文采用其提出的全耦合模型模拟地表径流和土壤水分运动，其关系式表示为：

两者之间水量交换的驱动因素主要为水力梯度，交换水量Qos为[1]：

式中：kso为垂直方向上的土壤饱和渗透系数张量，cm/s；hs为土壤水水头，cm；h0为地表水水头，cm；lso为耦合长度，cm；对于kr，当hs＞h0时，kr为地表的相对渗透率，当hs＜h0时，kr为土壤相对非饱和导水率。

1.1.4 模型参数的处理

采用van Genuchten模型来表示土壤水分特征曲线和饱和非饱和土壤水力传导率[31]：

式中：Ks为饱和水力传导度，cm/s；Se为有效饱和度，无量纲；h为土水势，cm；α为进气吸力倒数，cm-1；a和b是与土壤水分特征曲线相关的经验常数；l为孔隙连通性参数，对大多数土壤常取0.5；θr为残余体积含水率，cm3/cm3。

对于地表径流运动参数，kox和koy可以由曼宁方程推导求出：

式中：nx、ny分别为x、y方向上的曼宁糙率系数，s/cm1/3。

1.2 地表水土壤水运动与溶质运移全耦合模型

采用经典的对流弥散方程描述溶质在二维地表水与三维地下水中的运移，根据达西通量和溶质浓度得到地表水与土壤水的溶质交换量，在水分耦合模型的基础上建立水分运动与溶质运移耦合模型，两者采用相同的空间和时间离散。

土壤水中的溶质运移方程[32]：

地表水中的溶质运移方程[32]：

地表水土壤水之间的溶质交换量：

式中：q和qo分别是土壤水渗流通量和地表水渗流通量，cm/s；C和Co分别为土壤水和地表水中溶质的浓度，mg/cm3；D和Do分别为土壤水和地表水的水动力弥散张量，cm2/s；Ωo、Ωs和Ωos分别为地表水溶质的源汇项、土壤水溶质的源汇项、地表水和土壤水之间溶质的交换通量，mg/(L·s)；R和Ro分别为溶质在土壤水和地表水中的阻滞系数，无量纲；∇代表梯度算子，是在三维空间各方向上的全微分，∇ˉ代表平面上的二维梯度算子；CL+1为上游节点处的溶质浓度，mg/L，当水分由地表向地下补给时，CL+1是地表水中的溶质浓度，当水分由地下向地表补给时，CL+1是土壤水中的溶质浓度。

水动力弥散张量D和Do由下式计算：

式中：αl和αt分别为纵向和横向弥散系数，cm；|q|是达西通量的大小，τ是基质的弯曲度，无量纲；Dfree是自由溶液扩散系数，cm2/s；I为单位张量。

对于溶质阻滞系数R和Ro，可由下式给出[33]：

式中：ρb为土壤容重，g/cm3；K′为Freundlich吸附等温线的平衡分布系数。

2 模型验证

选取已发表的野外坡面降雨产流试验与室内土槽坡面氮素迁移试验对本文构建的模型进行验证。利用野外坡面降雨产流试验对水分运动耦合模型进行检验；坡面氮素迁移试验中包含硝态氮迁移过程，用来验证本研究中的水分运动与溶质运移耦合模型。通过比较地表径流量和径流溶质浓度的观测值和模拟值，来进一步评价模型效果。采用均方根误差（root mean square of error，RMSE)和平均相对误差（averaged relative error，ARE）作为判别指标，RMSE和ARE的数学计算公式为：

式中：Swsim,i是通过实测参数并优化参数进行建模得到的模拟值；Swobs,i是试验观测值；N为样本总数；RMSE和ARE的值越小代表拟合效果越好。当观测值和模拟值相同时，RMSE和ARE的值为0。

2.1 水分运动耦合模型的验证

算例1选自XING等[34]的野外边坡人工降雨试验，实验设置如图1所示，裸露的斜坡宽5 m，长10 m，试验期间没有作物生长。实验前在试验地块上施加一定强度的降雨，直到产生径流，以此对坡面进行预湿处理，保证各处理的初始含水率一致。试验过程中分别以75 mm/h和50 mm/h的雨强在土壤容重为1.45 g/cm3的不同坡度坡面进行试验，每次模拟降雨持续50 min，地表径流在坡面出流口处收集。详细实验步骤参见文献[34]。

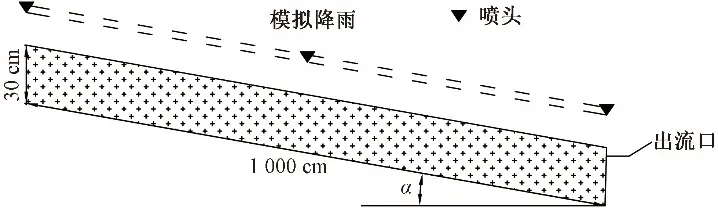
图1 实验设置示意Fig.1 Schematic diagram of the experimental setup

根据实验设置，本模型中将模拟区上部边界设置为降水输入边界，四周为渗流面边界，底部为透水边界，地表出流口为临界深度排水边界。在模型离散中，空间步长在坡面和垂直坡面方向均为10 cm，垂向上划分为10层。为在表层水流强交互作用处加密网格，设置上面5层网格尺寸为2 cm，下面5层网格尺寸为4 cm，模拟区域共生成56 661个节点。迭代计算时，设定初始时间步长0.001 s，最小时间步长乘数为0.5，最大时间步长乘数为5.0，最大时间步长为30 s，饱和度Sw迭代精度为0.05。模型计算所采用的主要参数可分为实测和经验参数两部分。实测参数直接从参考文献[34]中选取，参考文献中未提供的参数主要有van Genuchten模型中的参数，依据试验区土壤质地选取经验值并经过率定得到。模型主要输入参数如表1所示。

表1 模型主要参数Tab.1 Main parameters of the model

选取研究中的3种坡度（5°、10°和15°）和两种降雨强度（50 mm/h和75 mm/h）共6种试验情景，以其中50 mm/h降雨强度下3个不同坡度坡面的试验数据对本模型参数进行率定，75 mm/h雨强的3组试验数据用于验证。将整个模拟期内坡面出口处径流单宽流量的模拟值与实测值进行对比，两种降雨强度下不同坡度的产流过程分别如图2和图3所示。从图2和图3中可以看出，在几种实验情景下产流后的单位径流流量均急剧增加，后随时间推移逐渐趋于稳定。通常情况下，降雨初期土壤入渗能力受土壤水势影响较大。随着降雨入渗使土壤水分含量增大，土壤水势减小，使得土体渗透率快速减小，而后径流量随着渗透率的逐渐稳定也趋于平稳。

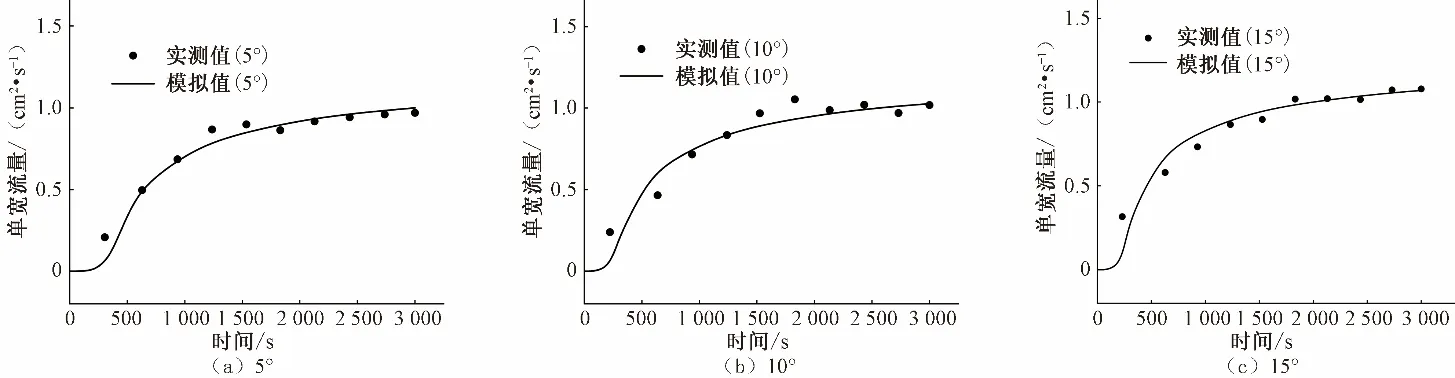
图2 雨强为50 mm下不同坡度坡面的单宽流量Fig.2 Unit width flux of different slopes under 50 mm rainfall intensity

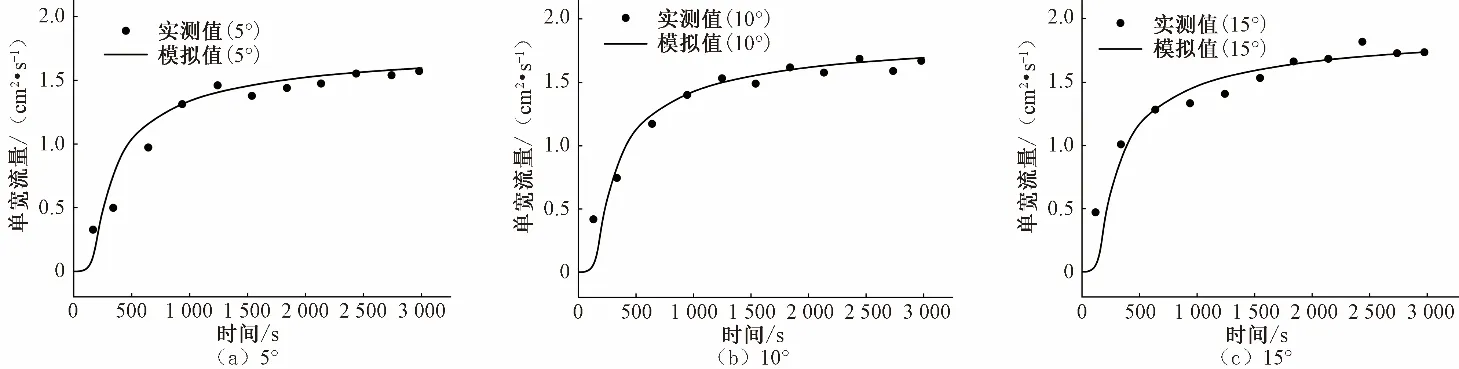
图3 雨强为75 mm下不同坡度坡面的单宽流量Fig.3 Unit width flux of different slopes under 75 mm rainfall intensity

地表径流过程同时受降雨强度和坡度的影响。由表2可以看出，模拟后期出流趋于稳定时，在75 mm/h的降雨强度下，坡度为5°、10°、15°的坡面出口处单宽流量分别为1.596 cm2/s、1.697 cm2/s、1.741 cm2/s。这是由于在径流过程中，当斜坡坡度增大时，径流沿坡面方向的重力分力随之增加，径流速度的提高缩短了入渗时间，降水渗入到土体的部分减少，从而产流量不断增大，因此同等降雨强度下，径流流量与坡面坡度呈现正相关关系。在50 mm/h的降雨强度下也可以观察到同样现象。数值模拟结果也与此前研究一致。在坡度为5°的坡面上，50 mm/h和75 mm/h的降雨强度下的坡面出口处单宽流量分别为1.001 cm2/s、1.596 cm2/s。即坡度一定的情况下，当雨强增大时，地表径流量随之增加，同时径流过程能够更快地趋于平稳。在对10°和15°坡面的模拟中也得到同样结果。这主要是由于降雨过程中土壤孔隙逐渐被水分填满，土体下渗强度在减小后趋于稳定，使得多余的水量积于地表形成径流。一般来说，随着降雨强度的增加，渗透率更容易达到稳定状态。

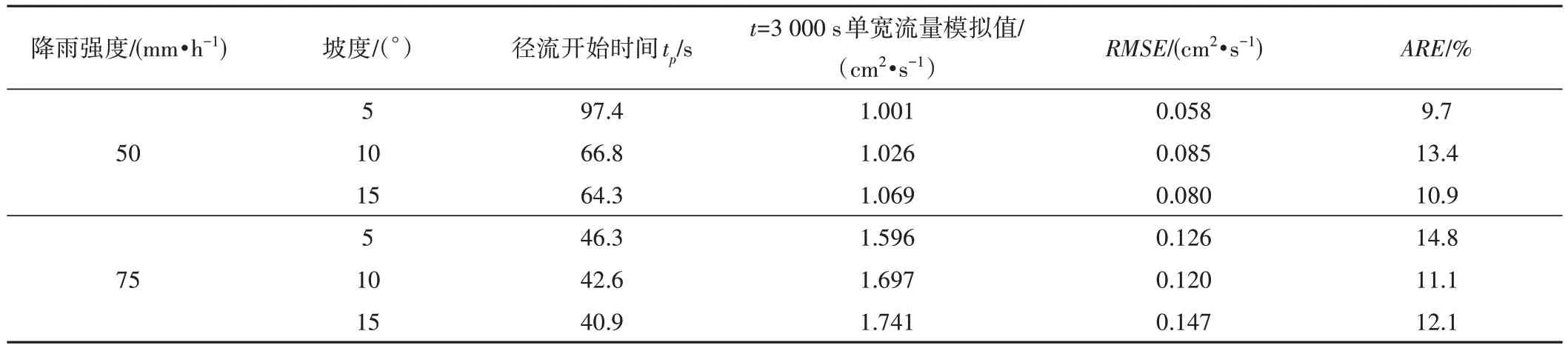
表2 不同雨强和坡度下的径流开始时间、稳定单宽流量及单宽流量实测值与模拟值误差分析Tab.2 Runoff start time，stable unit width flux and error analysis of measured and simulated values of unit width flux under different rain intensities and slopes

坡面产流速度也与降雨强度和坡度相关。由表2可知，在50 mm/h的降雨强度下，坡度为5°、10°、15°的坡面径流开始时间分别为97.4、66.8、64.3 s，说明降雨强度一定时，坡面产流速度随坡面坡度的增加而趋于加快。在75 mm/h的降雨条件下亦有此规律。这是由于降雨条件相同时，随着坡面坡度的增大，降雨的入渗损失减小，同时重力沿坡向的分力使水分在坡向的运动速度更大，土壤表面的水流汇集速度更快，从而使径流形成的时间更短。此外，对比相同坡度坡面在不同降雨强度下的产流时间，可以发现降雨强度越大时，坡面产流时间越短。一般情况下，随着降雨强度增大，土壤孔隙能够更快被填满，也提高了水分在地表的积累速度，从而使得产流时间更早。

不同降雨强度和坡度下模型模拟计算的评价结果列于表2。坡面单宽流量的RMSE值在0.058 cm2/s到0.147 cm2/s之间，ARE均在14.8%以内，且水分运动耦合模型的模拟结果与该算例实验数据拟合情况良好（图2和图3），验证了本文方法和程序的正确性及适用性。

2.2 水分运动与溶质运移全耦合模型的验证

算例2来自朱焱等[35]2017年的室内非饱和坡面降雨径流和氮素迁移土槽试验，试验包括2个长1.5 m，高0.6 m宽0.3 m的钢制土槽，坡角分别为8.85°和7.55°，编号分别为1号和2号。实验设置示意见图4。两个土槽试验的进行时间分别为3 260和3 200 s。试验期间，两土槽降雨强度分别为0.00 181、0.00 145 cm/s。详细试验步骤参见文献[35]。采用本文构建的水分运动与溶质运移耦合模型对该试验的地表径流过程和径流中硝态氮浓度进行模拟。

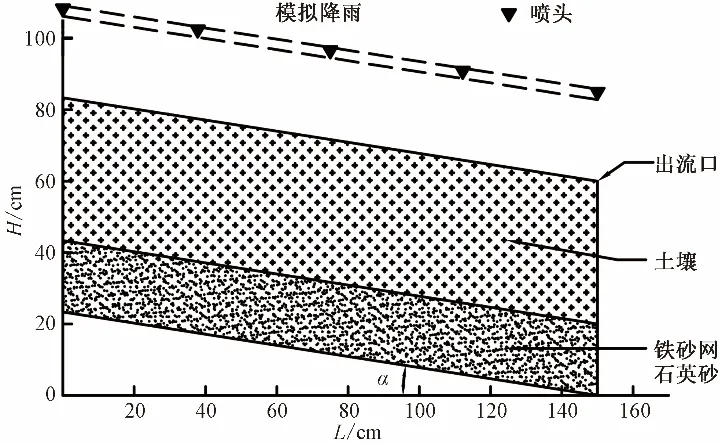
图4 土槽试验设置示意图（1号）Fig.4 Schematic diagram of the soil tank experimental setup（No.1）

根据试验建立三维模型，初始状态下土壤表层含有一定浓度的硝态氮，试验过程中上界面有指定强度和溶质浓度的降雨输入，因此将模拟区上部边界设置为降水边界和指定质量通量边界；钢制土槽四周不透水，因此侧向均为隔水边界；底部由铁砂网和石英砂，将其概化为透水边界；地表出流边缘设置为临界深度排水边界，使边界处的深度等于临界深度。采用等间距矩形网格对模拟区域进行空间离散，设置坡面方向网格尺寸为5 cm，垂直坡面方向尺寸为10 cm，垂向上剖分成20层。因土壤表层中含有一定浓度溶质，为在水分与溶质强交互作用处加密单元格，设置上面10层网格尺寸为0.5 cm，下面10层网格尺寸为3.5 cm，模拟区域共生成7 497个节点。两土槽模拟时长分别为3 260和3 200 s。在进行迭代计算时，设定初始时间步长0.001 s，最大时间步长乘数为5.0，最小时间步长乘数为0.2，最大时间步长为20 s，饱和度Sw迭代精度为0.01，溶质浓度求解迭代精度为1.0×10-10。溶质运移相关参数直接从文献中选取，因此利用试验的径流数据对模型水力参数进行率定后，即可根据径流中溶质浓度数据对水分与溶质耦合运动模型做出验证。试验条件与模型主要输入参数如表3所示。

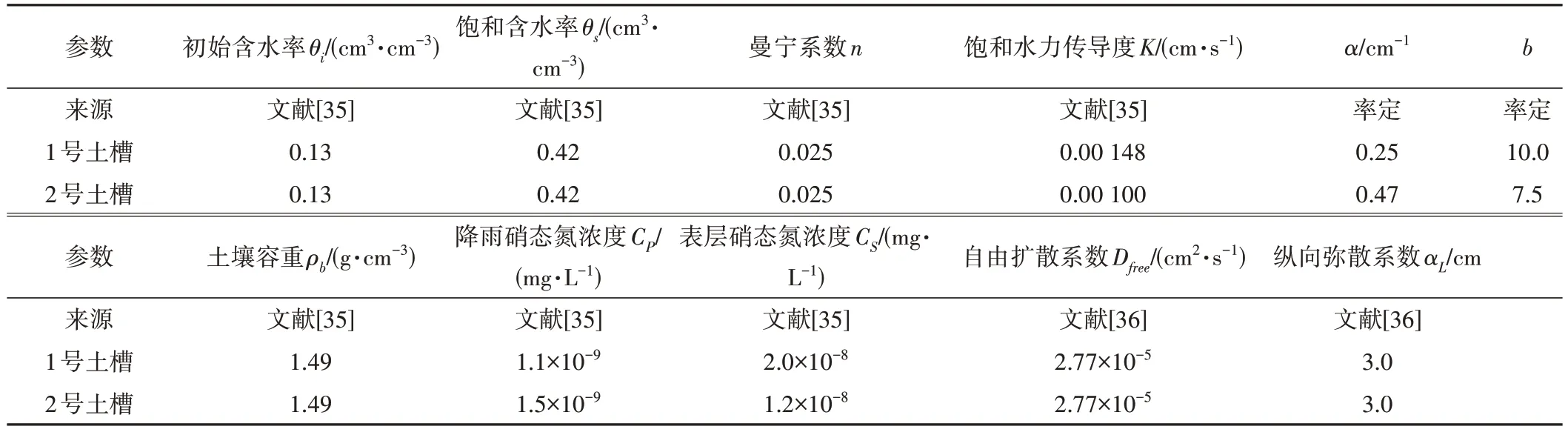
表3 土槽试验模型输入参数Tab.3 Input parameters of simulated soil tank test model

两土槽坡面出口位置的地表径流单宽流量、径流中硝态氮浓度的试验数据与模拟计算结果的拟合情况如图5所示。整体上看，针对坡面径流出口处单宽流量的模拟，在初始产流阶段与实测情况有所偏差。如图5（a）所示，1号土槽在初始产流阶段流量实测值波动较大，而数值模拟结果变化则较为平缓，如图5（c）所示，2号土槽在模拟前期的实测流量与模型模拟结果偏差较大，多点实测数据均大于模型模拟值。造成该现象的原因可能是降雨初始阶段非饱和坡面的入渗情况较为复杂，试验中的土槽坡面也并非完全均质平整，致使该阶段模拟结果产生偏差。随着试验的进行，坡面径流过程逐渐趋于稳定，后期实测流量与模型模拟结果的拟合情况相对较好。1号土槽单宽径流量计算的RMSE值为0.583 cm2/s，ARE值为11.8%；2号土槽单宽径流量计算的RMSE值为0.833 cm2/s，ARE值为21.5%。造成2号土槽径流计算误差较大的原因主要是由于该土槽的实测数据点分布较为离散，波动较大，而利用模型计算的径流与径流溶质浓度数值模拟结果均为平滑曲线，相对平缓。整体而言，本研究模型的径流模拟计算结果良好。

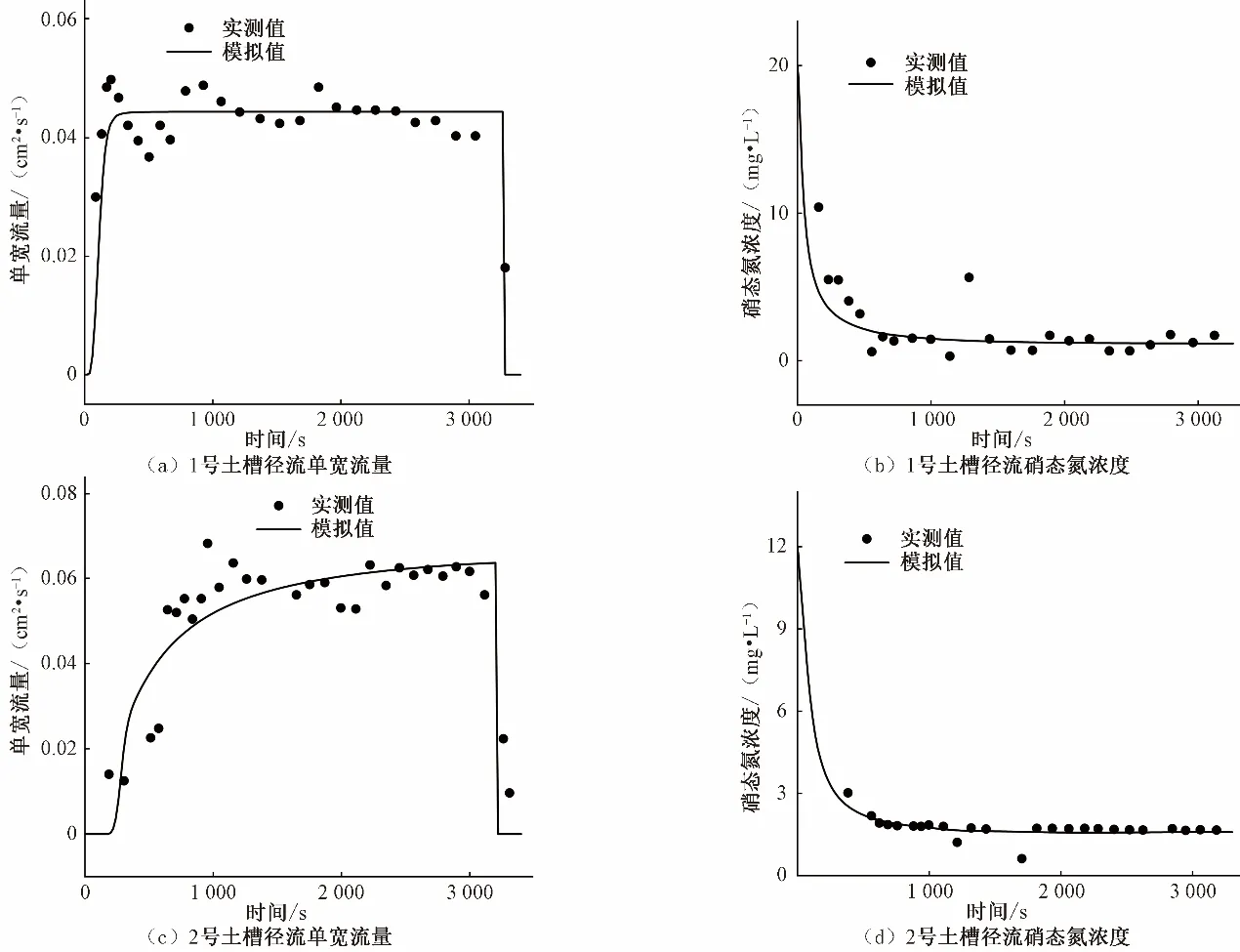
图5 两土槽坡面径流量、径流中硝态氮浓度的实测与模拟对比Fig.5 Comparison between the experimentally measured and model simulated values of runoff and nitrate nitrogen concentration on the slopes of the two soil trenches

两土槽径流中硝态氮浓度的变化过程如图5（b）和图5（d）所示，由于降雨与土壤中的硝态氮存在较大浓度差，表层土壤中的硝态氮在对流扩散作用的驱动下随径流不断流失，使得径流中硝态氮浓度呈现先急剧下降后趋于稳定的变化。模拟结果与试验值的偏差在模拟初期较为明显，多数模拟值均小于试验结果，可能是受径流计算偏差的影响。当1号土槽稳定出流且径流中硝态氮浓度变化相对平稳时，在1 285 s处有一实测的径流硝态氮浓度数据与整体偏离较多，为更准确评价模型的模拟效果，选择在误差计算时除去该点数据。1号土槽径流中硝态氮浓度计算的RMSE值为1.334 mg/L，ARE值为24.7%，2号土槽径流中硝态氮计算的RMSE值为0.248 mg/L，ARE值为12.1%。由图4-14-2可知，1号土槽在初始产流阶段流量实测值波动较大，且径流硝态氮浓度模拟值与实测值的误差主要是在模拟初期产生，故1号土槽硝态氮浓度计算误差较大的原因可能是受模拟初期径流计算偏差的影响。总体而言，模型模拟计算结果与试验数据拟合较好。综合以上分析，本文构建的水分运动与溶质运移耦合模型能够准确模拟地表径流过程及径流中硝态氮的浓度变化过程。

2.3 参数敏感性分析

在模型的构建过程中，通过引入耦合长度lso这一参数来实现水分和溶质在地表与土壤两者间运动迁移的耦合，因此选择分析该参数的敏感性。使用的敏感性分析方法是：通过调整模型中参数取值，比较模拟变量计算结果的变化情况，分析过程中采用控制变量法。具体来说，本文在最佳耦合长度lso的基础上分别上调（+）和下调（-）10%后进行模型计算，观察此参数对地表流量和径流中溶质浓度的影响。

算例1中降雨强度设置为50和75 mm/h，坡度设置为5°、10°和15°。算例1中情景1-6的降雨强度和坡度分别为50 mm/h和5°、50 mm/h和10°、50 mm/h和15°、75 mm/h和5°、75 mm/h和10°、75 mm/h和15°，计算结果如表4所示。由表4可知，不同的耦合长度设置对地表径流和径流氮素浓度模拟的影响不同。随着耦合长度的增加，模拟的地表单宽流量和径流硝态氮浓度均有不同程度的改变，但总体上看，两者的变化均与耦合长度参数呈正相关关系。从表4中还可以看出，在对算例1的6种实验情景的模拟中，耦合长度lso变化10%对地表出流量的改变量均在0.5%以内；在对算例2两个土槽试验的模拟中，耦合长度lso变化10%对地表出流量和径流硝态氮浓度模拟结果的改变均小于5%，因此可认为模型中该参数不敏感。

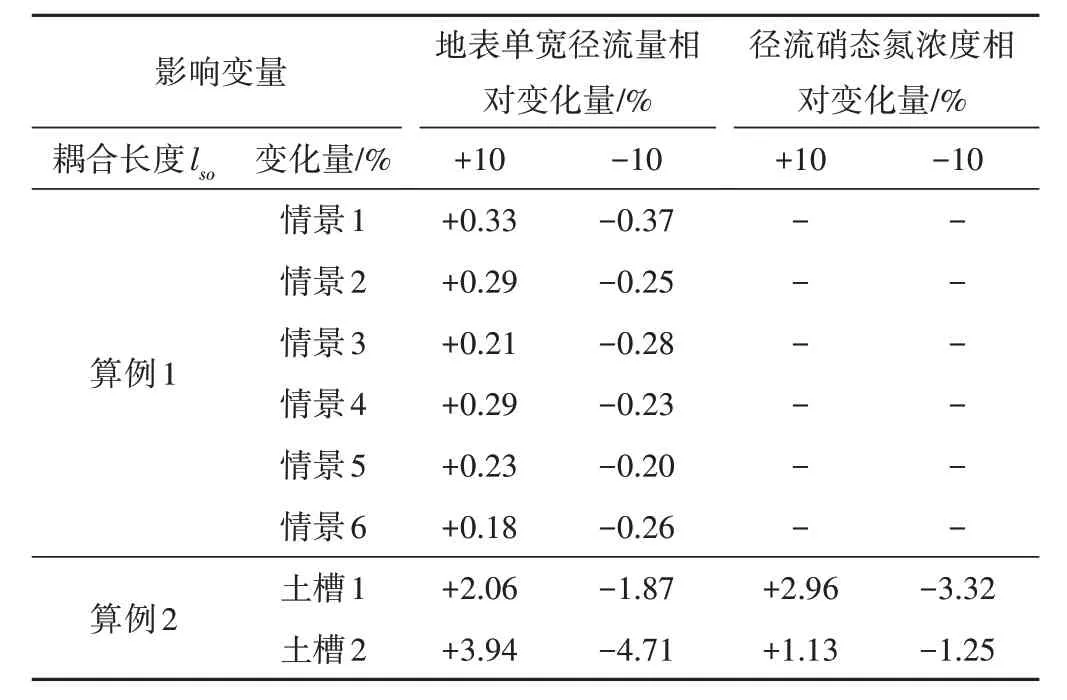
表4 参数敏感性分析Tab.4 Sensitivity analysis of parameters

3 结 论

本文采用二维扩散波方程和传统的三维Richards方程描述地面径流和土壤水分运动，选用双层结点法对两者进行耦合，根据达西定律和地表与土壤水中的溶质浓度，计算地面径流和土壤水分的溶质交换量，从而构建地表水土壤水运动与溶质运移全耦合数值模型。野外边坡降雨产流试验观测数据与模型模拟结果的对比显示，本模型水分计算的平均相对误差小于14.8%，均方根误差小于0.147 cm2/s。室内坡面径流与氮素迁移试验监测数据与模型模拟结果的对比显示，本模型水分计算的平均相对误差小于21.5%，均方根误差小于0.833 cm2/s，硝态氮浓度计算的平均相对误差小于24.7%，均方根误差小于1.332 mg/L。说明本文构建的全耦合模型对地表水土壤水水分运动与溶质运移过程的模拟准确可靠，模型对地表和地下不同模块间的耦合关系表述合理。