基于GA-FUZZY-PID算法的精准施肥控制系统研究

2023-08-28王昊张立新吴勋王梦帆李靖闫梓洋

节水灌溉 2023年8期

王昊，张立新，吴勋，王梦帆，李靖，闫梓洋

（石河子大学机械电气工程学院，新疆石河子 832000）

0 引言

棉花作为纺织业的主要原材料，是一种与国家经济发展密切相关的战略资源。相关数据表明，在2022年，新疆地区的棉花产量539.1 万t，占全国棉花总产量的90%以上，是我国最大的棉花产区[1]。棉花生长发育过程需要大量用水、大量用肥，但新疆地区年均蒸发量远大于年均降水量，水资源严重短缺。针对这一问题，新疆地区棉田灌溉采用水肥一体化技术[2]。

水肥一体化技术是一种广泛应用于新疆棉花种植的节水节肥新技术。水肥一体化技术的原理是通过对棉田内传感器所获取的监测数据进行智能化分析和处理，利用智能算法推导出灌溉决策并反馈至终端执行。该技术实现了棉田水肥精准施肥，提高了土壤的水肥利用效率，达到保护环境、提高产量、节省劳力的效果[3]。

目前水肥一体化技术的控制方法主要集中在PID控制算法与模糊控制算法。但传统PID算法对于时变对象和非线性系统的处理性能差，易引起超调，产生振荡[4]；模糊算法中参数设定大多基于人工经验，存在控制欠细腻的问题。因此，通过结合遗传算法计算简单、功能强、优化效果好的特点，实现对肥料流量快速有效的调整，降低了流量调节过程中时滞性、非线性等因素带来的影响[5]。

1 棉田施肥灌溉系统总体结构

棉田施肥灌溉系统主要由蓄水池、储肥罐、过滤器、电磁阀、流量传感器、压力表、软管泵等装置组成，棉田施肥灌溉系统总体结构图如图1所示。其中，储肥罐的过滤器两端安装了压力表，用于判断过滤器的堵塞情况，实现定期对过滤器的清洗更换，防止肥料中的固体沉积物堵塞管道[5]。灌溉管道上安装有稳压器，确保灌溉时管路的压力稳定。各管道均装有单向阀，防止管内液体的倒流。在灌溉管道上装有流量计，用以监测灌溉流量。施肥系统的输送装置选择软管泵，三相异步电动机与软管泵泵体相连，被输送物料由软管包围，不与其他零件接触。当转子转动时，随着滚轮位置的变化，软管被压缩和回弹，使泵产生吸入和压出作用，达到输送肥料的目的。系统通过改变与软管泵相连的变频器的频率来精确调节软管泵出口的施肥流量。

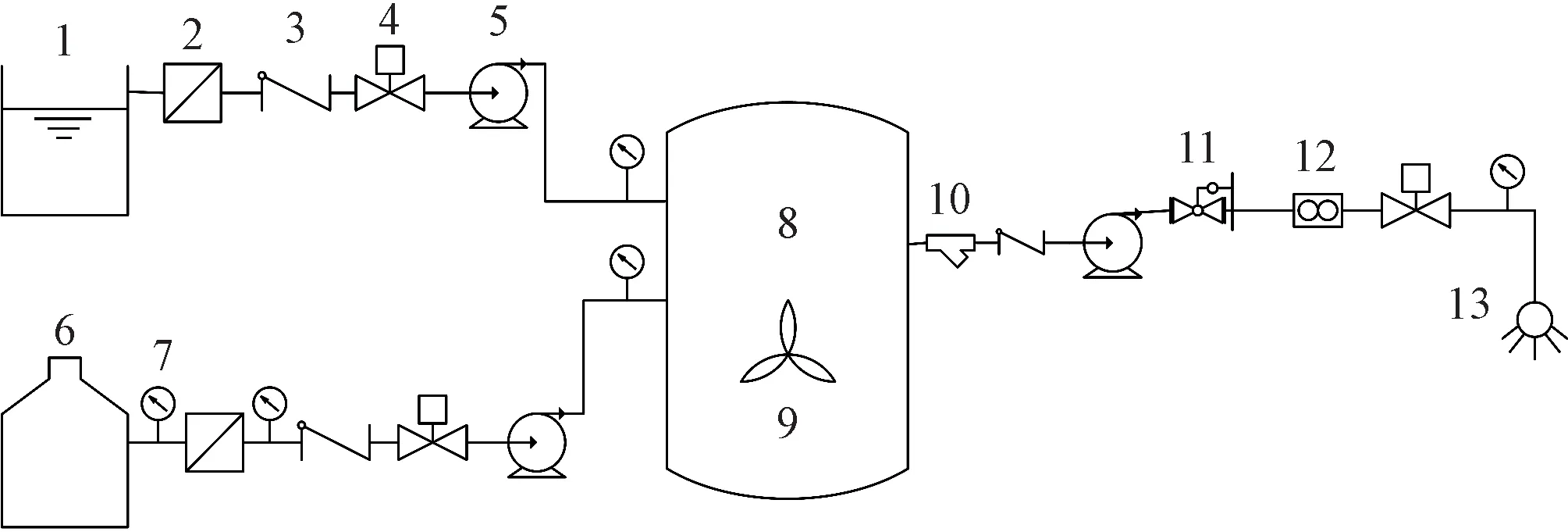
图1 棉田施肥灌溉系统结构Fig.1 Structure diagram of cotton field fertilization and irrigation system

棉田施肥灌溉系统的工作流程如下：将蓄水池和储肥罐的电磁阀开启，相应线路的软管泵将水和肥料按比例抽入混肥罐中，通过搅拌泵进行搅拌混合，当搅拌混合结束后，混合肥液由灌溉管道的软管泵输送到棉田。当灌溉管道上的流量传感器监测到肥料流量与设定值出现偏差时，系统将自动调整混合罐出口处软管泵流量，以保持稳定状态。

2 棉田施肥灌溉系统控制模型建立

基于施肥灌溉的特性和系统的复杂程度，选择一阶惯性加延迟环节的传递函数作为数学模型[4,5]，数学模型方程如下：

式中：K为增益系数；τ为延迟时间；T为时间常数；s为复频率。

将施肥流量的期望值作为开环系统的输入，采样时间间隔设定为1 s，获得流量变化的数据。采用一阶近似方法，在Matlab软件中对数据进行拟合，得到系统的增益系数K为0.06、延迟时间τ为8 s、时间常数T为28。

2.1 PID控制器设计

PID控制器由比例部分、积分部分、微分部分组成，具有操作简单、鲁棒性高等优势，在工业领域具有广泛的应用[6]。在实际应用过程中，控制器输入常为设定值r(t)与输出值y(t)之差e(t)，输出控制量u(t)由差值e(t)决定，输出控制量u(t)具体表达式如下：

式中：Kp为比例增益；Ti为积分时间常数；Td为微分时间常数。

采用Cohen-Coon参数整定法初步整定KP、Ti、Td3个参数。Cohen-Coon参数整定法的主要工作原理如下：通过配置系统的主导极点使对象的过渡曲线按4∶1的衰减率衰减，从而得到最优的PID参数整定值[7]。参数整定经验公式如下：

根据棉田施肥灌溉系统的数学模型，将对应参数值代入式（3）中，并通过试凑法对PID的各系数进行调整，使设定量与反馈量之间的误差不断减小直至满足系统要求。参数最终设定为：Kp=20，Ki=2，Kd=12。其中，Ki为积分增益，Ki=Kd为微分增益，

2.2 模糊算法优化设计

模糊PID控制器是通过模糊算法对PID控制器参数进行动态调整，使系统达到良好的控制效果。本文设计的模糊优化系统为双输入三输出系统，模糊控制方法为Mamdani直接推理法，即模糊控制规则共由49条语句构成，但实际的输入数据仅与其中4条语句有关，利用这4条被激活的语句进行推理计算得到控制目标的输出量[8]。模糊控制器决策模型如图2所示。

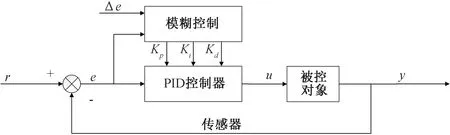
图2 模糊控制器决策模型ΔeFig.2 Fuzzy controller decision model

该决策模型的输入变量为流量偏差值e和流量偏差变化率Δe，输出变量为比例增益Kp、积分增益Ki、微分增益Kd。流量偏差值e和流量偏差变化率Δe的量化因子为K1、K2，比例增益Kp、积分增益Ki、微分增益Kd的比例因子为K3、K4、K5。设定流量偏差值e和流量偏差变化率Δe的模糊论域为[-2, 2]，根据相关经验，则量化因子K1=1、K2=1；比例增益Kp、积分增益Ki、微分增益Kd的模糊论域均为[-3, 3]，量化因子分别设定为K3=5、K4=0.6、K5=3。输入输出变量的模糊集论域分为7个模糊集合，分别由NB（负大）、NM（负中）、NS（负小）、ZO（零）、PS（正小）、PM（正中）、PB（正大）语言值来表示[9]。模糊控制规则根据专家经验给出，比例增益Kp、积分增益Ki、积分增益Kd的控制规则分别如表1～表3所示。

表1 比例增益Kp的控制规则Tab.1 Control rules for proportional gain Kp

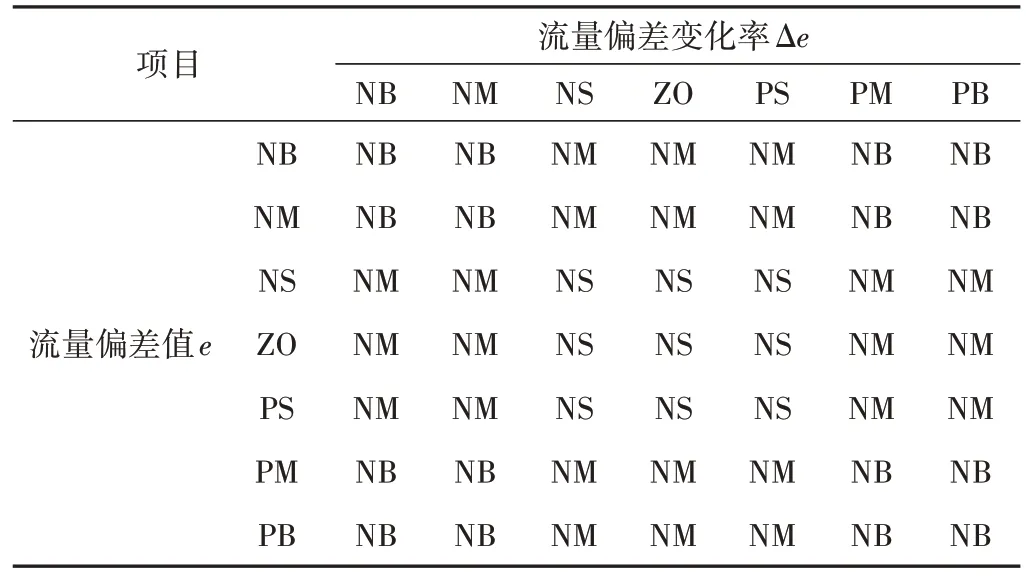
表2 积分增益Ki的控制规则Tab.2 Table of control rules for integral gain Ki

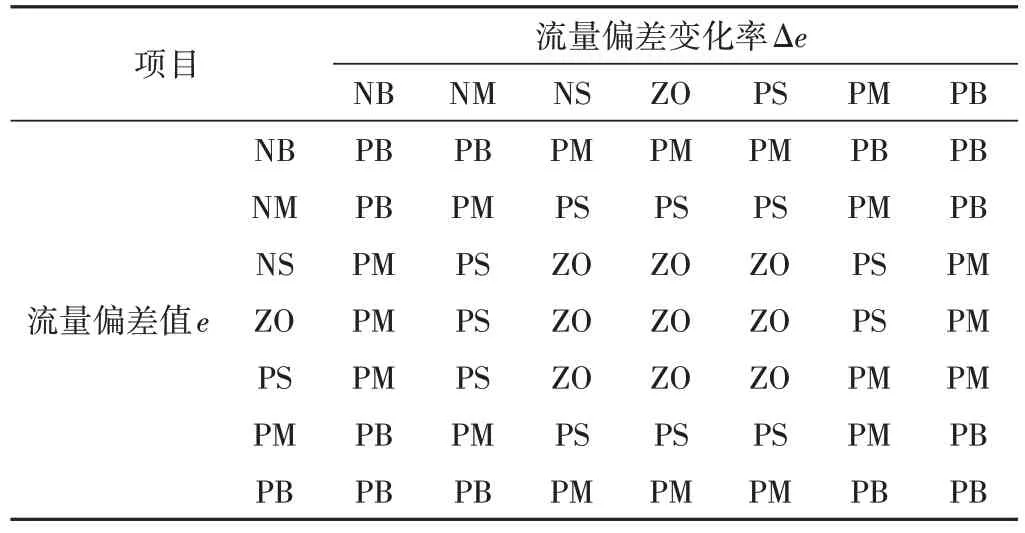
表3 微分增益Kd的控制规则Tab.3 Table of control rules for integral gain Kd

实际控制过程中，单条模糊控制规则对应的模糊推理语句为多重多维条件语句，其基本形式为：

公式（4）表明若流量偏差值e的输入语言值为A，流量偏差变化率Δe的输入语言值为B，则根据模糊规则推理，比例增益Kp的输出语言值为C，积分增益Ki的输出语言值为D，微分增益Kd的输出语言值为E。总的模糊控制规则R是49条多重多维条件语句的并运算。为提高系统的灵敏度，系统模糊控制器的输入输出量均采用三角形隶属度函数。流量偏差值和流量偏差变化率的隶属度函数如图3所示，比例增益Kp、积分增益Ki、微分增益Kd的隶属度函数如图4所示，比例增益Kp、积分增益Ki、微分增益Kd的特性曲面分别如图5～图7所示。

图3 流量偏差值e和流量偏差变化率Δe的隶属度函数Fig.3 The membership function of flow deviation value e and flow deviation change rate Δe

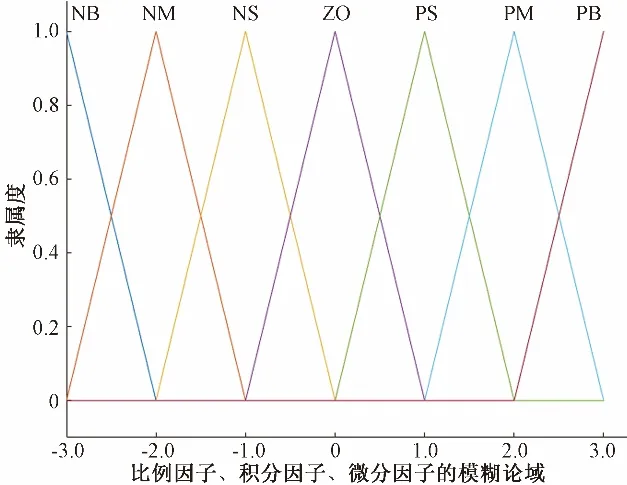
图4 比例增益Kp、积分增益Ki、微分增益Kd的隶属度函数Fig.4 Membership functions of proportional gain Kp, integral gain Ki,and differential gain Kd

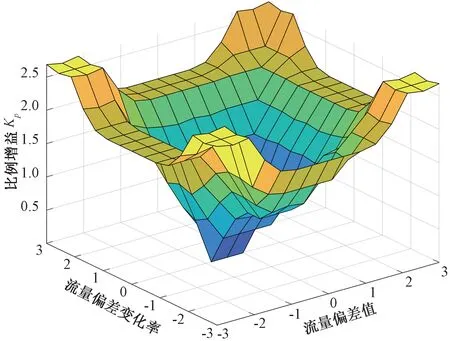
图5 比例增益Kp的特性曲面Fig.5 Characteristic surface of proportional gain Kp

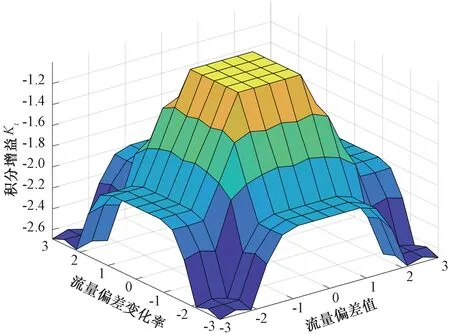
图6 积分增益Ki的特性曲面Fig.6 Characteristic surface of integral gain Ki

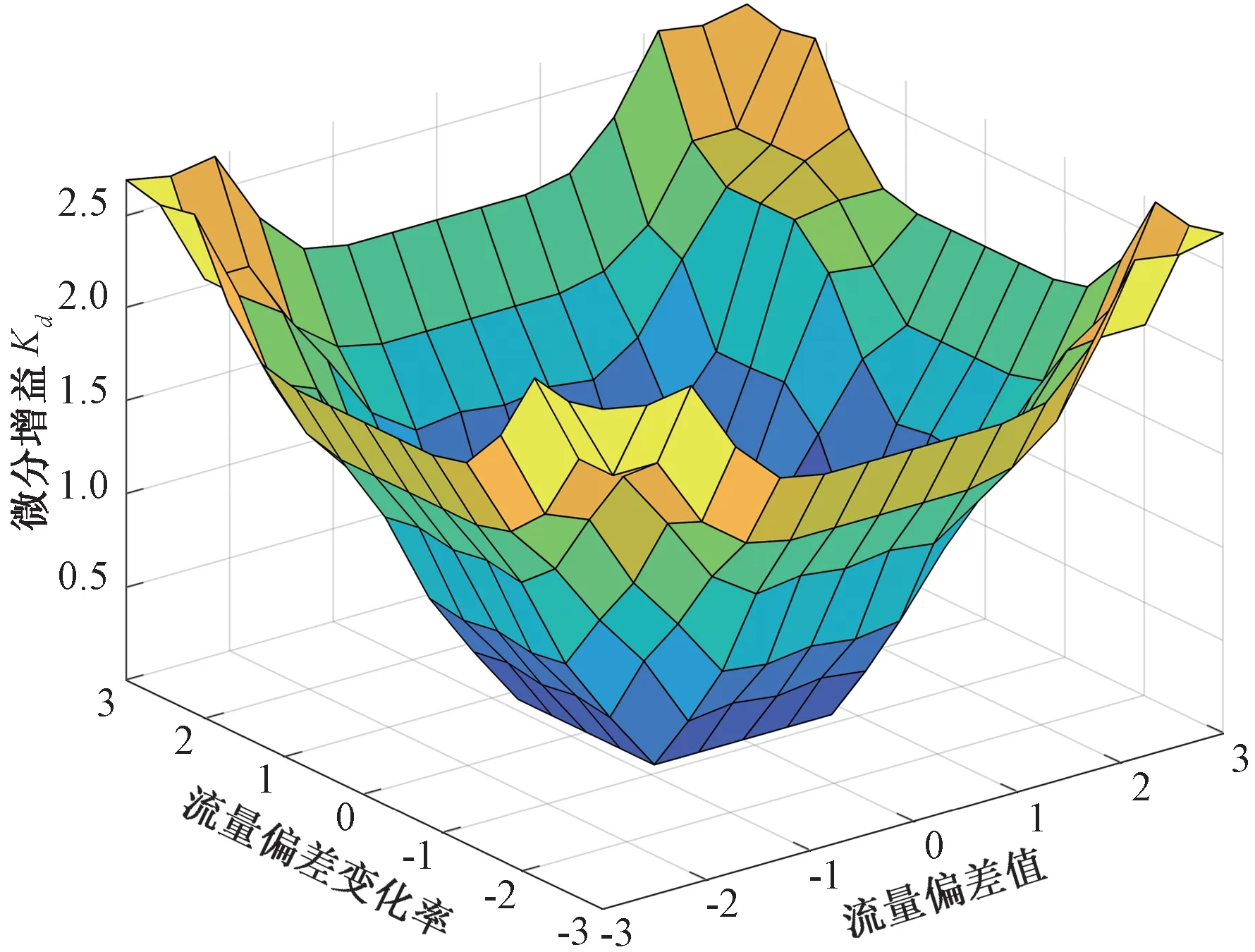
图7 微分增益Kd的特性曲面Fig.7 Characteristic surface of differential gain Kd

系统的清晰化方法选用重心法，其公式如下：

式中：K(i)表示某一输出变量模糊集合的隶属函数有值处；P为隶属函数有值处的个数；μk(i)为有值处的隶属函数值。

2.3 遗传算法优化设计

遗传算法作为一种高效启发式算法，具有隐藏的并行性，是从解空间中多个体出发，寻找最优解的算法，具有高效稳定的特点，在自动控制、图像处理、生产调度问题等方面有着广泛应用[9]。图8为遗传算法流程图。

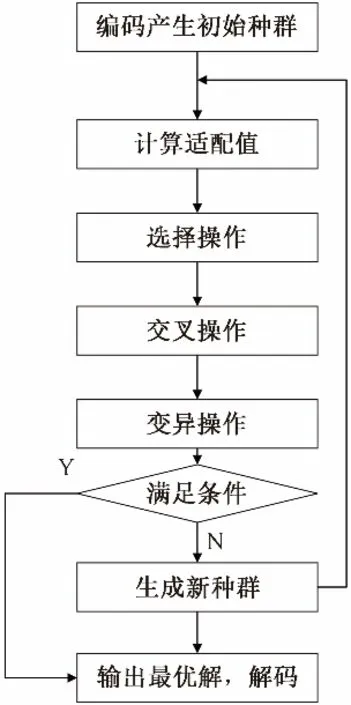
图8 遗传算法流程Fig.8 Flow chart of genetic algorithm

（1）初始种群。使用遗传算法对比例因子K3、K4、K5进行优化，编码方式采用浮点数编码方法，将K3、K4、K5编为三维列向量，以提高运行效率，初始种群为随机生成的20个初值。

（2）适应度函数。适应度函数体现了个体的优劣性，为选择提供了标准与动力[10]。控制器的瞬态性能指标主要有上升时间、稳态时间、最大超调量[11]。上升时间、稳态时间反映了控制器的响应速度，最大超调量反映了控制器控制过程的稳定性。针对文中确定的模型而言，误差函数W公式如下：

式中：T表示使用PID算法输出到达设定值的时间；y(t)表示系统实时最终输出值；y0表示目标函数的设定值；tα表示使用优化算法后输出最终到达设定值并平衡的时间；ym表示系统最终输出的最大值。

根据专家经验及实践，当系统越差时，误差W值将越大，个体保留至下一代的可能就越小，因此可采用误差W作为目标函数来评价系统的性能，设置系统的适应度函数等于目标函数，将问题转换成求适应度函数最值问题。适应度函数计算公式为：

（3）选择操作。是指在生物遗传进化过程中，使适应度更强的个体遗传到下一代的机率更大，选择的主要目的是避免基因缺陷，提升全局的收敛性与计算效率。本文使用的选择机制为常规的轮盘赌选择法，即个体的适应度函数值越小，被选择的概率就越大。

（4）交叉操作。是指群体内的个体随机两两配对，以一定概率交换部分染色体。通过2个染色体的交换组合，产生新的优良品种。本文使用的交叉机制为单点交叉，即随机设置一个交叉点，在该点后字符相互交换，设定交叉概率为0.6。

（5）变异操作。是指以一定概率随机改变个体中某个串的位置，防止丢失一些有用的遗传因子，决定了遗传算法的局部搜索能力，设定变异概率为0.1。

终止条件：遗传算法可通过对最大迭代次数的设定或使适应度函数到达特定范围来终止程序运行。本文采用设定最大迭代次数作为终极条件，设定迭代次数为100代，最终通过解码得到最优解。3种不同的初始设定值在100次迭代过程中的适应度函数变化曲线如图9所示。

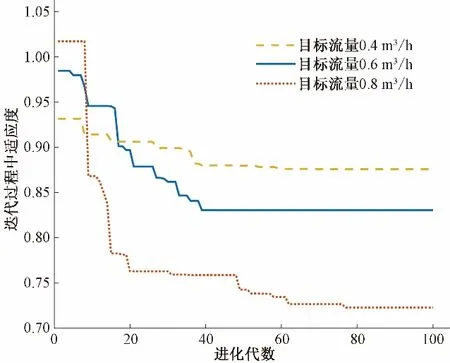
图9 不同设定流量值的迭代过程中适应度函数变化曲线Fig.9 Adaptability function change curve during iteration with different set flow values

3 仿真分析

为验证本文设计的GA-Fuzzy-PID算法策略的优越性，在Simulink中分别搭建了PID控制器、Fuzzy-PID控制器、GAFuzzy-PID控制器模型，如图10所示，并对仿真结果进行比较。在棉花实际灌溉过程中，流量选择{0，1 m3/h}，因此算法应适应范围内任一流量设定值[12]。当设定流量值在该范围内取值时，为验证GA-Fuzzy-PID算法是否优于其他2种算法，选取目标流量值为0.6 m3/h、0.8 m3/h、0.4 m3/h 3种不同目标设定流量值进行仿真，0.6 m3/h的仿真结果如图11所示，并给出3种不同设定流量值的性能指标如表4～表6所示，讨论不同设定目标流量值下3种算法的性能指标。

表4 设定流量值为0.6 m3/h时的3种控制器性能指标Tab.4 Three controller performance indicators when the flow rate is set to 0.6 m3/h

图10 Simulink控制系统模型Fig.10 Simulink control system model diagram

在设定流量值为0.6 m3/h的情况下，如表4所示，PID最大超调量为45.29%，稳态时间为263.0 s，远落后于其他2种算法。Fuzzy-PID算法的使用，使得最大超调量稳定在18.67%，稳态时间在188.5 s，相对于PID算法降低了系统最大超调量，缩短了稳态时间。GA-Fuzzy-PID算法的最大超调量则降低至1.68%，稳态时间分别缩短至115.5 s，表明使用遗传算法对Fuzzy-PID算法优化效果明显。

在设定流量值为0.8 m3/h的情况下，如表5所示，PID最大超调量为43.30%，远高于其他2种算法。稳态时间为279.0 s，远落后于其他2种算法。Fuzzy-PID算法的最大超调量稳定在17.59%，稳态时间在197.5 s，表明算法具有良好性能。GA-Fuzzy-PID算法的最大超调量则减少至0.87%，稳态时间缩短至120.0 s，表明GA-Fuzzy-PID算法在大流量设定值时，能够适应设定流量值的变化。

在目标流量为0.4 m3/h的情况下，如表6所示，PID最大超调量为42.35%，稳态时间为248.0 s。Fuzzy-PID算法的最大超调量稳定在19.74%，稳态时间为207.0 s，相对于PID算法性能有所提升。GA-Fuzzy-PID算法最大超调量减少至4.14%，稳态时间缩短至147.0 s，表明GA-Fuzzy-PID算法在低设定流量值时，仍具有优越性。

表6 设定流量值为0.4 m3/h时的3种控制器性能指标Tab.6 Three controller performance indicators when the flow rate is set to 0.4 m3/h

由表4～表6可知，PID算法表现差，3种不同设定流量值下的最大超调量均在40%以上，稳态时间在240 s以后，性能指标远落后于其他2种算法。Fuzzy-PID算法的使用，使得最大超调量稳定在20%以内，稳态时间在200 s左右，相对降低了系统最大超调量，缩短稳态时间，具有良好的工作性能。GA-Fuzzy-PID算法的使用，使得最大超调量稳定在5%以内，表明GA-Fuzzy-PID算法具有更好的调控系统，避免系统严重过冲。稳态时间稳定在150 s以内，表明GA-Fuzzy-PID算法响应速度快，能快速将系统调整到设定状态上。在设定流量值的范围内，GA-Fuzzy-PID算法能够适应设定流量值的变化，具有优异的性能。

4 精准施肥控制系统流量调节实验

为了验证GA-Fuzzy-PID算法的实用性能，本文搭建了相应的流量调节实验平台，以STM32F103ZET6单片机为控制元件，将I/O口接收的流量传感器的信号在单片机内部进行运算，转换成可变化的电压信号，对变频器的输出频率作出调整，最终改变混合罐出口处的肥料流量。软管泵的最大输送流量为1 m3/h，额定功率为1.5 kW，额定电压为380 V。变频器额定功率为2.2 kW，输出频率为0～400 Hz，额定电压为380 V。流量传感器选择美控中国的不锈钢电磁流量计，型号为LDG-MIK，精度为0.5%。操作过程中将混合罐中液体的体积保持在50 L。流量调节实验平台如图12所示。

图12 实验平台Fig.12 Test platform

本次实验设定流量为0.6 m3/h，对PID控制器、Fuzzy-PID控制器、GA-Fuzzy-PID控制器进行测试。实验结果如图13所示，3种控制器性能指标如表7所示。

表7 实验流量值为0.6 m3/h时的3种控制器性能指标Tab.7 Three controller performance indicators at a test flow rate of 0.6 m3/h

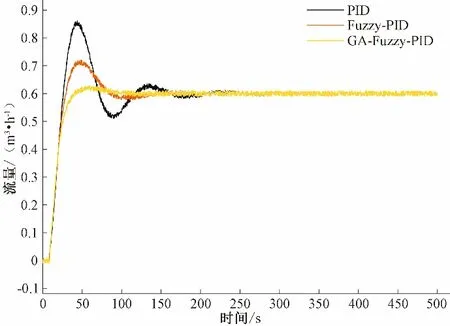
图13 实验流量为0.6 m3/h时3种控制器的调控曲线Fig.13 Control curves of three controllers at a test flow rate of 0.6 m3/h

实验设定目标流量为0.6 m3/h，性能指标如表7所示，PID算法的最大超调量为41.93%，稳态时间为257.1 s，远落后于其他2种算法。Fuzzy-PID算法的使用，使得最大超调量稳定在20.07%，稳态时间在182.4 s，相对于PID算法降低了系统最大超调量，缩短了稳态时间。GA-Fuzzy-PID算法的最大超调量则降低至4.41%，稳态时间缩短至126.3 s，说明使用遗传算法优化后的Fuzzy-PID控制器具有优异的性能。