有机朗肯循环机器学习模型关键参数集识别
2023-08-28闫栋杨富斌张红光许永红吴玉庭
闫栋, 杨富斌, 张红光,3, 许永红, 吴玉庭,3
(1.北京电子科技职业学院, 北京 100176; 2.北京工业大学 环境与生命学部, 北京 100124; 3.传热与能源利用北京市重点实验室, 北京 100124)
2030年实现碳达峰、2060年实现碳中和是时代赋予能源领域的神圣使命,实现中低温热能高效热功转换是节能减排的关键。有机朗肯循环(organic Rankine cycle, ORC)以其结构简单、适应性强、转化效率高等优点成为极具潜力的中低温热能热功转换技术之一。目前在太阳能[1]、地热能[2]、生物质[3]等可再生能源开发,以及工业过程节能[4-5]、内燃机余热利用[6-8]等方面的应用得到了广泛研究。
ORC系统参数对其性能有着重要影响。学者们分别就工质特征参数[9]、透平效率[10]、循环水流量[11]、工质流量[12]、工质泵效率[13]对ORC系统性能的影响进行了深入研究。ORC是一个由多部件组成的循环系统,许多系统参数都会对系统性能产生影响,这些系统参数间不可避免地就会出现冗余信息。另一方面,ORC系统性能不可能完全由1或2个关键系统参数决定。这就需要识别出ORC系统的关键参数集,准确描述ORC系统参数与系统性能的关联规律。
由于不可逆损失的存在,常规的热力学方法难以实时准确可靠的描述ORC系统参数与其性能之间的关联规律。统计学方法可以从信息学角度描述系统参数与系统性能的关联关系,为建立准确可靠的ORC系统模型提供了可能。Bademlioglu等[14-15]采用了Taguchi和ANOVA方法获得了ORC系统参数对系统性能的贡献率和重要性排序。Kalina等[16]建立了ORC黑箱模型识别最佳的系统运行工况。Larsen等[17]建立了ORC系统线性统计模型研究系统参数与系统性能的关联规律。另一方面,ORC系统参数高度耦合(例如,蒸发温度与蒸发压力之间的强相关关系),理论研究和简单试验分析难以实现参数解耦。主成分分析(principal component analysis, PCA)可获得多个参数之间的隐含数据结构,并通过构建包含参数信息的主成分从而实现参数的解耦。此外,它还可以实现参数降维,降低分析的难度。基于PCA的优势,已经在热力学领域的研究中得到了广泛应用[18-20]。
ORC系统是一个多部件联合运行的热功转换系统,系统运行过程中有很多参数(如:蒸发器出口压力和温度、冷凝器入口压力和温度、工质泵效率、膨胀机轴效率、工质流量、管路压力损失和系统热损失等)都会对系统性能产生影响。在这些参数中,蒸发器出口压力和温度、冷凝器入口压力和温度、工质泵效率和膨胀机轴效率是6个基本系统参数,其它参数对系统性能的影响也是通过改变这6个基本参数而实现的。
本文选择蒸发器出口压力pe和温度Te、冷凝器入口压力pc和温度Tc、工质泵效率ηP、膨胀机轴效率ηSSE6个基本参数作为初始变量,并对其进行相关性分析和主成分分析。随后,将ORC系统热效率ηORC作为系统性能指标,建立ORC系统参数与ηORC之间的机器学习模型。最终,根据回归模型的预测性能利用枚举法识别出ORC系统关键参数集。
1 有机朗肯循环性能试验
该ORC系统的示意如图1所示。该系统主要包括3个子循环:导热油循环、有机朗肯循环和冷却水循环。

图1 有机朗肯循环系统示意Fig.1 Schematic diagram of the ORC test system
1.1 导热油循环
在该试验系统中,导热油循环为系统提供热源。导热油循环主要由3个部件构成:导热油锅炉、油泵和蒸发器。在试验过程中,导热油首先在导热油锅炉中被电阻丝加热,然后进入蒸发器,将热量传递给ORC系统工质,最后在油泵的作用下重新进入导热油锅炉。
1.2 有机朗肯循环
在该试验系统中,ORC系统主要由4个部件组成:工质泵(离心泵)、蒸发器(管壳式)、膨胀机(单螺杆式)和冷凝器(管壳式)。R123[21]作为系统工质。在试验过程中,工质首先在工质泵的作用下进入蒸发器吸收热量成为高温高压蒸汽。随后,高温高压蒸汽进入膨胀机做功。最终,完成做功后的工质被冷凝器冷却为液态工质,再重新进入工质泵开始新的循环。
循环过程的T-s图如图2所示。ORC中所用传感器的主要参数如表1所示。这些传感器的位置分布如图1所示。

表1 ORC系统所用传感器的参数Table 1 Parameters of measurement sensors in the ORC system
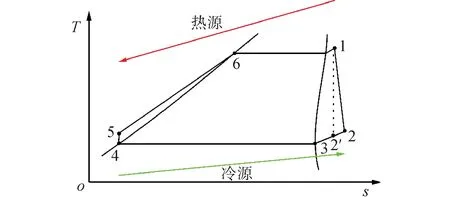
注:图中数字1~6依次表示工质高温高压状态、膨胀做功后的过热状态、膨胀后的等压干饱和状态、膨胀后的等压湿饱和状态、工质泵加压后状态、工质泵加压后工质湿饱和状态。图2 有机朗肯循环T-s图Fig.2 T-s diagram of the ORC system
1.3 冷却水循环
在该试验系统中,冷却水循环为试验系统提供冷源。冷却水循环主要由3个部件组成:水泵、冷却塔和冷凝器。冷却水循环从系统冷凝器中带走热量,并将热量释放到环境中。
1.4 试验设计
在该ORC系统中开展了一系列试验工作。研究ORC的pe、Te、pc、Tc、ηP和ηSSE系统参数对系统性能的影响规律。该试验系统使用的单螺杆膨胀机对应的最佳工作效率时的转速约为2 500 r/min, 因此,在试验过程中膨胀机的转速被设定在2 500±30 r/min的范围内。当该试验系统暖机工作完成后,通过调整导热油循环和工质泵的运行状态,使蒸发器出口的工质参数从初始状态(T=80.50 ℃,p=0.424 MPa)缓慢变化到最终状态(T=120.60 ℃,p=1.054 MPa)。在试验过程中,所有的测量数据均被实时记录。ORC系统的试验数据变化范围如表2所示。在试验过程中共计获得了2 043个有效数据点,受文章篇幅所限,本文仅在表3中展示了部分原始试验数据。ORC系统ηORC的不确定度ΔY为:

表2 ORC系统试验数据变化范围Table 2 Variation ranges of ORC system test data
表3 部分原始试验数据Table 3 Part of the original experimental data
(1)
式中:Y为目标变量;ΔXi为测量变量的不确定度。ORC系统热效率的不确定度最大值、最小值及平均值分别为0.000 34、0.000 17和0.000 255。
2 机器学习模型
2.1 主成分分析
PCA是一种常用的分析多维数据的统计学方法,以最少的信息损失为前提,将原有变量转变为几个线性无关的综合指标,并将这些综合指标称为主成分PCs[22]。PCs按照包含变量方差信息的大小分为第1主成分PC1、第2主成分PC2、第3主成分PC3等。PC1包含了最多的变量信息,接下来依次是其他PCs。
PCA的计算步骤为:1)将原始数据矩阵X标准化为新矩阵X*;2)计算新矩阵X*的系数矩阵R;3)利用Jacobi方法求解特征方程∣λI-R∣=0获得特征值;4)计算获得各主成分的贡献率和累积贡献率以及载荷因子。
在ORC系统中,系统参数常常呈现出强关联性。PCA可以减少系统参数的维度,识别出系统参数的基本数据结构。并且通过建立新的变量,避免了系统参数之间的强关联性。
2.2 回归模型
在ORC系统中,由于压力损失、散热损失、机械损失等不可逆损失的存在,传统的ORC热力学模型的准确度会降低[23]。机器学习模型是基于统计学原理,在试验数据的基础上训练获得,因而有较高的准确性。本文分别建立ORC系统的基于多元线性MLR、人工神经网络BP-ANN和支持向量机SVR的回归模型。回归模型是以pe、Te、pc、Tc、ηP和ηSSE为变量,以ηORC为目标函数。试验数据集按照5∶1∶1的比例分别划分为训练集、验证集和测试集。在构建多元线性回归模型时,由于没有用到验证集,因此将训练集和验证集组合在一起作为训练集。基于这3种机器学习方法建立ORC模型过程为:
1)建立MLR模型,用多元线性方程来直接描述变量与目标函数值的关联规律;
2)建立BP-ANN模型。BP-ANN是一种误差反向传播的人工神经网络[24]。它以适应性强、非线性、高精度等优点在ORC研究领域得到了广泛应用[24]。本文采用Matlab工具箱建立BP-ANN模型。所使用的隐含层层数为1,神经元个数为10,学习率为0.1,训练函数为Levenberg-Marquardt;
3)建立SVR模型。SVR是支持向量机的重要分支,是支持向量机中的超平面决策边界,是一种性能强大的机器学习方法[25]。本文采用libsvm-3.24工具箱建立SVR模型,采用网格法获得最优参数。
2.3 枚举法特征选择
特征选择是简化数据维数的重要手段,它从最初的特征集合中按照一定的规则删除冗余以及不重要的特征,从而获得一个最优特征集合的过程。在机器学习中常采用特征选择的方法来应对高维问题[26-28]。枚举法是利用计算机运算速度快、准确度高的优点,对有穷集合逐一进行检查,从而确定符合要求的集合。通常,枚举法首先确定枚举对象、枚举范围和判定条件,然后枚举可能的集合并验证是否是最佳集合。利用枚举法进行特征选择是一个在相关参数中确定出最优参数集的有效方法。本文通过枚举法在系统参数数量从1变化到6的过程中,从不同的系统参数组合中筛选出使回归模型性能达到最优的参数组合,称这个参数组合为关键参数集。
3 机器学习模型性能分析
3.1 系统参数相关性和主成分分析
在对ORC系统参数进行主成分之前,首先对系统参数的相关性进行检查。在本文中,将pe、Te、pc、Tc这4个系统参数定义为工质状态参数;将ηP和ηSSE定义为设备运行效率参数。该6个系统参数的相关系数如表4所示,具有较强的相关性,其中工质状态参数之间的相关性最强,相关系数均超过0.971;设备运行效率参数与工质状态参数之间的相关性稍弱;设备运行效率参数之间的相关性最弱,其相关系数为0.814。由此可知,设备运行效率参数是相对独立的2个参数。系统参数的各主成分载荷因子及特征值如表5所示。PC1、PC2、PC3、PC4、PC5和PC6依次代表了ORC系统参数的6个不同的主成分。系统参数不同的PCs对总体变量信息的贡献率及累积贡献率如图3所示。PC1的贡献率为94.33%,PC1和PC2的累积贡献率已经超过97%,因此需要对PC1和PC2进行深入分析。对于PC1,4个工质状态参数的载荷因子相当,且均大于设备运行效率参数,这表明PC1包含了更多的工质状态变化信息。在PC2中设备运行效率参数的载荷因子明显大于比在PC1中的大,这意味着PC2中包含了更多的设备效率参数。因此,PC1可以定义为工质状态参数指标,PC2可以定义为设备运行效率参数指标。
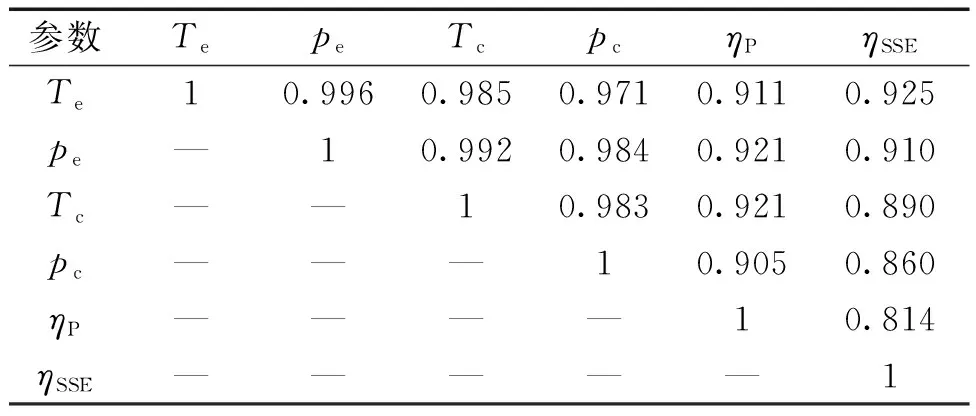
表4 系统参数之间的相关性系数Table 4 Correlation coefficients between the system parameters
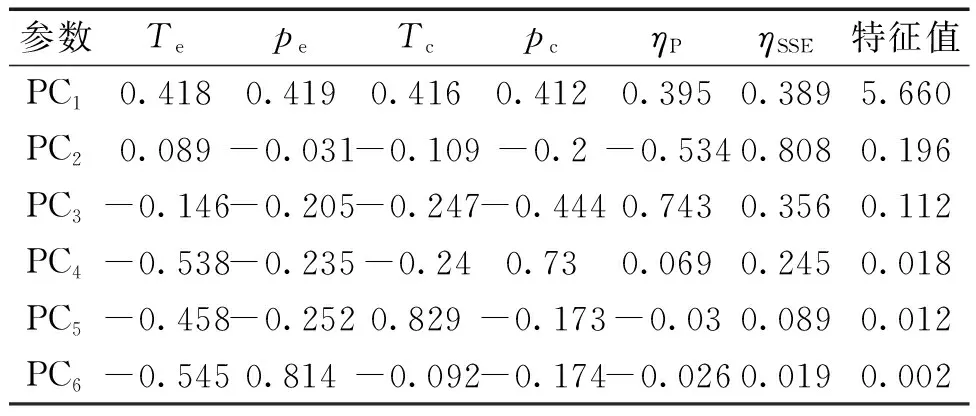
表5 系统参数各主成分的载荷因子及特征值Table 5 PCA factor loadings and eigenvalues of system parameters
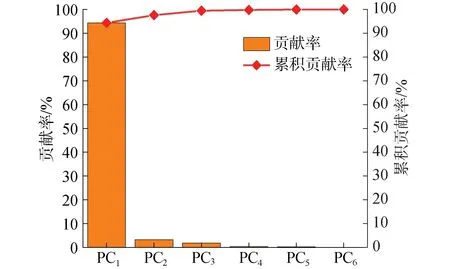
图3 各主成分对变量信息的贡献率和累积贡献率Fig.3 Contribution percentage and cumulative contribution percentage of the PCs
对PC1与PC2与设备性能的相关性进行分析,发现与ORC系统性能的关联规律。PC1与PC2与ηORC的相关性分别为0.958 4和0.173 0。表明PC1对于ηORC表现出了很强的相关性,远大于PC2和ηORC之间的相关性,由此可以看出ORC系统性能受工质状态参数的影响超过了受设备运行效率的影响。尽管PC2与ORC系统性能的相关性较低,但PC2包含了系统运行必不可少的设备运行效率的参数信息,对建立ORC系统模型是必要的。
3.2 模型性能对比
决定系数R2与均方误差EMSE是评价回归模型性能的2个重要指标。基于MLR、BP-ANN、SVR方法建立的ORC回归模型的R2和EMSE分别如表6所示。基于3种方法建立的ORC系统ηORC模型的R2均超过0.99。且采用3种方法建立的ORC系统ηORC模型的均方误差均低于2.8×10-7。对比3种方法建立的ORC回归模型的性能,可以看出MLR方法虽然精度比BP-ANN和SVR方法略低,但是对ORC系统性能的预测已经达到了相当高的精度。为了提高模型的可解释性与计算的方便性,本文选用了MLR方法在PCA分析的基础上建立ORC系统回归模型,简称PCA-MLR模型。

表6 PC1与PC2和ORC系统性能之间的相关系数Table 6 Correlation coefficients between each PC and ORC system performance
3.3 关键参数集识别
ORC系统关键参数集的选取是获得准确系统性能的前提,对于实际ORC系统,测量的变量有很多,然而并非这些变量都会对系统性能产生影响,且由于变量间强关联关系的存在,这些变量未必都是造成系统性能改变的直接原因。另一方面,ORC系统包含了多个热力过程,系统性能并非由单一的关键变量完全确定的。此外,从统计学角度来看,选取过多的参数会造成模型的过拟合,过少的参数会降低模型的精度。因此要获得准确的ORC系统性能,首先需要识别出系统关键参数集。
基于建立的PCA-MLR模型,采用枚举方法依次减少系统参数的变量个数,根据PCA-MLR预测模型精度的变化,逐步确定关键系统参数,并最终确定关键参数集。在确定关键参数集的过程中,当所选择的变量个数大于1时,采用的PCA-MLR模型是基于第1和第2主成分建立的;当系统参数个数为1时,所采用的PCA-MLR模型是仅基于第1主成分建立的。另外,在此过程中PCA-MLR的预测性能是基于测试集分析获得的。
随着系统参数数量变化,ORC系统参数的筛选结果如下:当变量个数从1增加到6的过程中,依次增加的变量为Te、ηP、ηSSE、pe、pc和Tc。系统参数数量变化过程中,最优的PCA-MLR模型的R2变化如图4(a)所示。随着变量个数从1变化到6,PCA-MLR的R2呈现出先增大后减小的变化规律,在变量个数为3时取得最大值,结合筛选变量结果,可以确定出此时的变量集合为(Te、ηP、ηSSE)。由此可知,提高ORC系统蒸发温度、提高工质泵效率、提高膨胀机轴效率可以明显提高系统热效率。系统参数数量变化过程中,PCA-MLR模型预测ηORC的MSE变化规律如图4(b)所示。MSE的变化呈现出与R2一致的变化规律。MSE随着变量个数从1变化到6,先减小后增大,在变量个数为3时取得最小值。结合PCA-MLR模型R2和EMSE的变化规律及枚举法所筛选出的关键参数,可以确定出ORC系统的关键参数集为(Te、ηP、ηSSE)。
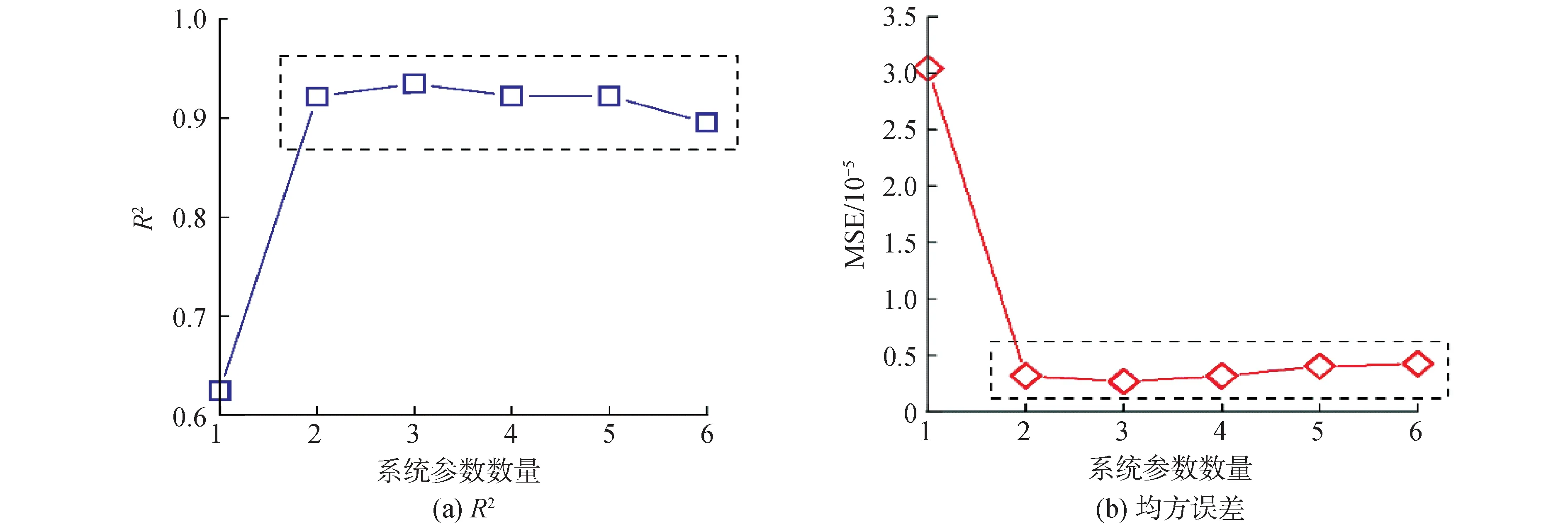
图4 不同数量系统参数建立PCA-MLR模型的R2与均方误差对比Fig.4 R2 and MSE of the PCA-MLR models using different numbers of system parameters
以6个系统参数建立的PCA-MLR模型ηORC的平均误差为1.66×10-3;而基于关键参数集建立的PCA-MLR模型ηORC的平均误差为1.44×10-3,平均误差降低了13.36%。基于关键参数集建立的PCA-MLR模型的绝对误差如图5所示。从图中可知ηORC的绝对误差范围为-0.05%~0.05%,此时模型已获得较优的预测精度。
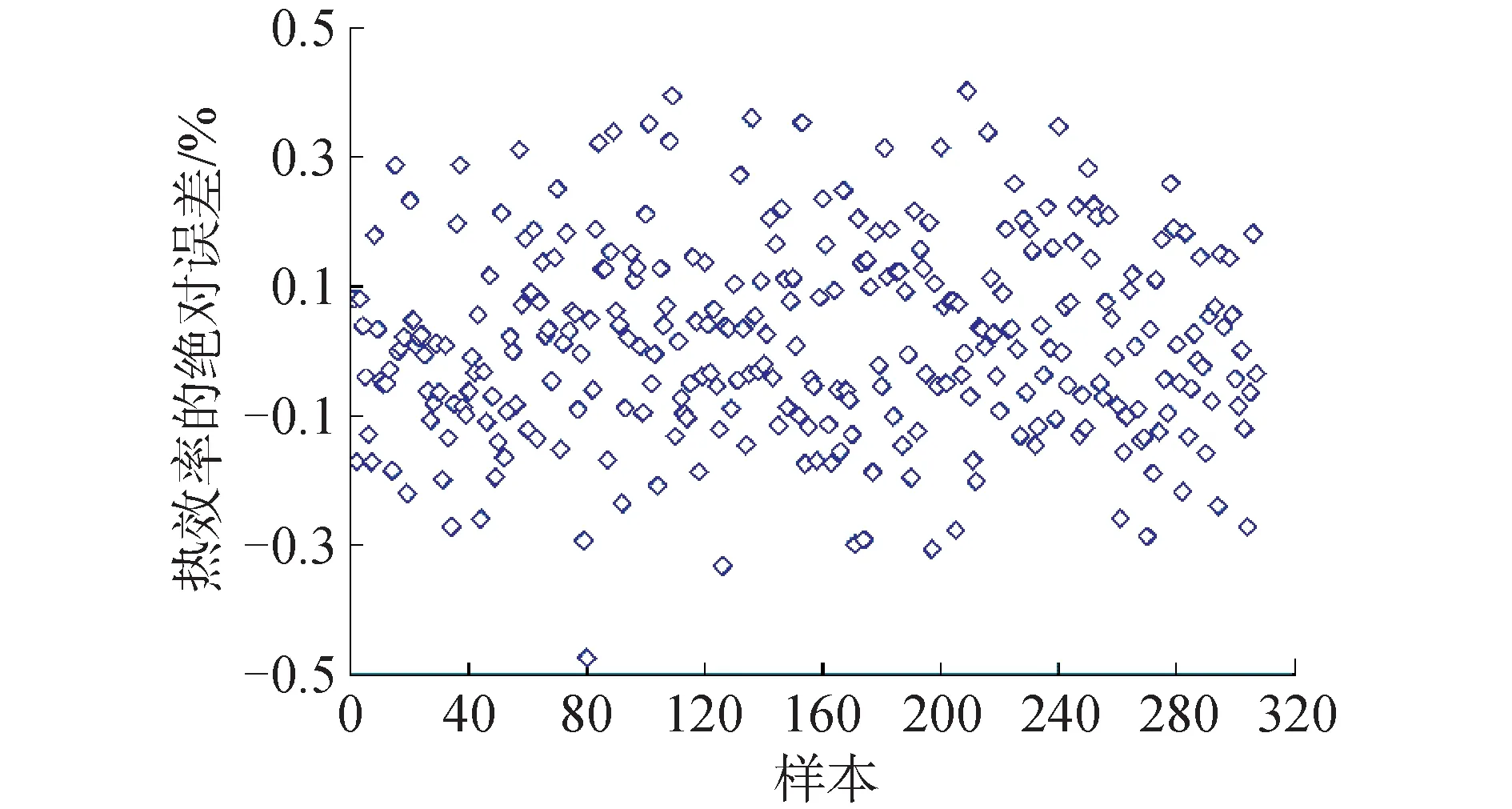
图5 基于关键参数集的PCA-MLR模型系统热效率的绝对误差Fig.5 Absolute error of the PCA-MLR model for thermal efficiency based on key parameter subset
4 结论
1)基于关键参数集建立的PCA-MLR模型可以使平均误差降低13.36%。采用关键参数集建立ORC系统机器学习模型,可以有效提高模型精度。
2)6个系统参数,相互之间均表现出明显的相关性,工质状态参数对系统性能的影响超过了设备运行效率参数的影响。调节系统运行时,优先改善工质状态参数可以提高ORC系统热效率。
