基于机器视觉的圆孔类尺寸精确测量

王若瑾，张旭

（201620 上海市 上海工程技术大学 机械与汽车工程学院）

0 引言

随着制造业的不断发展和工业水平的提高，对于工业零件尺寸测量的精度与速度要求越来越高。以孔类尺寸为例，当前工业检测中仍然以内径百分表或千分表为主要测量方法，传统人工检测手段存在效率低、对检测人员技术水平及经验要求高等问题，基于机器视觉的测量方法正凭借其低成本、非接触、简单高效等优点逐步成为机械零件尺寸测量的革新手段。

为实现高精度的工件尺寸自动化测量，传统的机器视觉尺寸测量算法主要依赖图像采集、图像预处理、边缘提取、数据拟合4 部分，这4 部分的共同进步推动尺寸测量算法精度的提升。在传统算法基础上，王高杰等[1]通过研究人工标志定位点的分布对单目相机位姿解算精度的影响，针对人工标志的布设和点位选择给出了合理的建议和指导，有助于提高相机标定的准确性，从图像采集部分减少误差，为后续图像处理打下了良好基础。图像预处理的作用在于消除图像中的无关信息，恢复有用的真实信息；王智文等[2]提出了一种基于多元统计模型的分形小波自适应图像去噪算法，在有效去噪的同时能够保持图像的精细结构。边缘提取作为基于机器视觉的尺寸测量算法中最为关键的部分，近年取得了长足进步；童胜杰等[3]提出一种基于2阶微分算子和数学形态的改进工件边缘检测方法，在去除工件表面划痕的同时提高了边缘清晰度和峰值信噪比；李凯等[4]融合了各向同性和自动各向异性高斯核边缘检测方法的优势，提出了一种加入边缘强度修正因子的边缘检测算法，获得了更优的噪声鲁棒性和弱边缘检测能力。随着精度要求的提高，以上单像素边缘已经不能满足实际需求，因此边缘检测算法进一步深入到了亚像素边缘，亚像素边缘检测技术主要分为3 类：基于矩的[5-6]、基于拟合[7-8]的和基于插值[9]的。其中，矩法准确性高但抗噪能力差且计算时间长；插值法的计算量相对较小，且具有较强的抗噪能力，但其定位精度较低；拟合法虽受拟合曲线限制，但具有较强的抗干扰性，定位精度也较高。数据拟合部分则影响着尺寸测量结果的直接输出，针对离群点会对拟合结果产生影响的问题，郭斯羽等[10]应对不同边缘点数量的实验条件分别提出了一种基于截断最小二乘法和2 种基于双点移除法的改进椭圆拟合算法。

为应用于实际测量系统，本文建立了一套结合改进Canny 和拟合法亚像素边缘提取的圆孔类尺寸测量方法，通过对标准内径环规的内径边缘进行检测完成像素标定，再通过针对圆孔类样本的曲线边缘检测进行尺寸测量，从而实现对圆孔类尺寸的高精度测量。

1 优化Canny 的像素级边缘检测

较为经典的像素级边缘检测算子大致可分为1 阶微分算子和2 阶微分算子。其中，1 阶微分算子（如Roberts 算子、Sobel 算子、Prewitt 算子等）的基本原理是通过对目标微分突出其灰度值的变化，将灰度变化值较高的部分视为边缘点，计算简单快速，但同时存在检测得到的边缘较粗且容易得到虚假边缘的缺点，因此通常仅适用于精度要求较低的场景。Laplace 算子是基于2 阶导数的边缘检测算子，不依赖边缘方向，对孤立点和阶跃型边缘点定位准确，但对噪声敏感且容易丢失边缘信息，故而通常不以其原始形式进行边缘检测。Canny 算子[11]一经提出便凭借其较为平衡的边缘检测与去噪效果一跃成为最受广泛应用的边缘检测算子。

原始Canny 算子的基本流程：首先采用高斯滤波对输入图片去噪，接着通过计算差分1 阶偏导得到图像的灰度梯度的大小及方向，然后经由非极大值抑制对边缘进行细化，最后通过双阈值的设置对图像进行滞后连接，得到完整的目标图像边缘轮廓。

但传统的高斯滤波存在会丢失边缘细节信息的固有弊端，而相较于同样具有边缘保持特性的双边滤波，由于引导滤波[12]的时间复杂度与窗口大小无关，故有计算速度更快的特点，且能够克服双边滤波可能引入“梯度反转”伪影的问题。为此，本文对传统Canny 中的滤波部分进行改进，利用具有良好保边效果的引导滤波代替高斯滤波对图像进行去噪处理。引导滤波示意图如图1 所示。

图1 引导滤波示意图Fig.1 Schematic diagram of guided filter

另外，在双阈值选取部分，为实现针对不同光源、拍摄环境均能获得自适应阈值的选取，本文通过灰度迭代来获取高低阈值，即选取图像灰度均值为初始阈值，再对高于初始阈值和低于初始阈值的部分分别求取均值，对得到的2 个均值再做平均得到新的阈值。当前后2 次阈值差小于迭代终止条件时完成选取，否则继续迭代至获得最佳阈值。其中，迭代终止条件可根据灰度直方图中的双峰收敛情况而定，以终止条件选择灰度差大于双峰各自内部灰度上下限的宽度为宜。改进后的Canny 边缘检测具体流程如图2 所示。

图2 改进Canny 滤波部分流程图Fig.2 Flow chart of improved Canny

2 基于像元分割的拟合高斯曲线亚像素边缘检测

边缘模型根据其灰度切面大致可分为：阶跃型、斜坡型和屋顶型[13]3 种，而实际中由于数字图像的边缘不可避免地存在被模糊和带有噪声，故而边缘灰度切面常被视为更加接近灰度斜坡。如图3 所示，图3（a）中的灰度值差别是受聚焦机理和电子元件影响产生的，可以看出越靠近实际边缘位置灰度变化最多；由图3（b）可见，当灰度值差分达到最大时即为实际边缘点；图3（c）显示灰度差分的外包络线接近高斯曲线。考虑到图片生成中存在的模糊效应及噪声中存在的主要部分为高斯噪声，因此考虑测量系统的实时性和准确性，本文选择使用高斯模型进行拟合更符合实际情况。

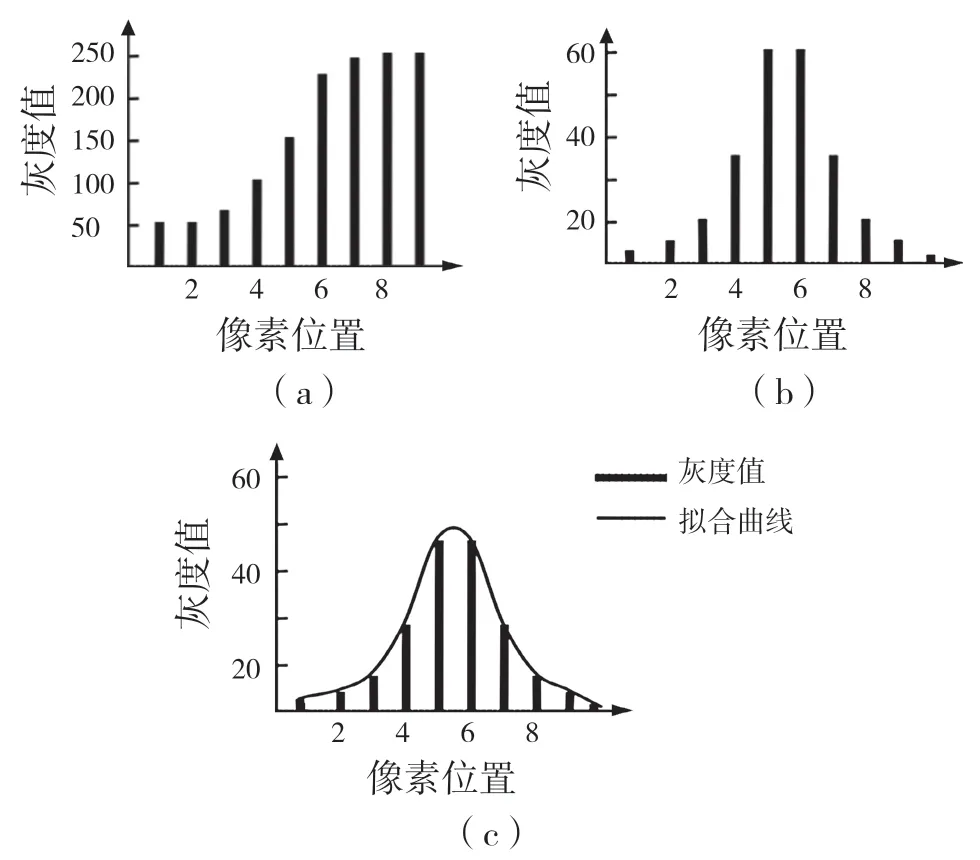
图3 斜坡型灰度图Fig.3 Grayscale image of slope

采用改进Canny 算子得到粗提取的像素级边缘检测结果后，再利用改进Sobel 算子的Scharr 算子求得每个单像素边缘点处的梯度幅值及方向，Scharr 算子的1 对卷积模板为

式中：GX——水平方向梯度算子；GY——竖直方向梯度算子。

具体在运算中，表现为每个像素灰度值与卷积模板对应位置的元素进行卷积运算，得到该点处的灰度梯度大小为

考虑开方带来的计算复杂度，常选用式（4）代替式（3）

则其对应的梯度方向为

接着，在边缘法线方向上对梯度幅值进行采样。由于拟合过程本质上是使真实数据曲线与拟合函数之间误差最小化，故采样点的选取十分重要。本文选择沿着每个边缘点所在的法线方向取若干个像素点，并将这些像素点向法线投影得到采样点（为兼顾算法的准确性和实时性，本文选择提取5 个采样点）。如图4 中，虚线网格表示图像整像素单元，实线方框为经过改进Canny 检测到的像素级边缘点，实线箭头所示为边缘的法线方向，A、B、C、D、E 点分别向梯度方向的投影点即为所取采样点，由于采样点不在整像素位置，故要获得采样点处的梯度幅值，需通过像元分割的方法将灰度法线方向上图像的最小单位进行细化分割，能够提高灰度图特征点的提取精度。

图4 拟合点的选取Fig.4 Selection of fitting points

由于双三次插值能够克服最近邻插值的不连续性与双线性插值中可能导致的细节退化等问题，为提高分割精度，本文设计使用双三次插值并借助采样点周围16 个像素点的梯度幅值与其变化率综合计算，实现采样点梯度幅值的获取。

具体来讲，用于拟合梯度曲线的高斯模型为

式中：μ——均值，也即所求亚像素的位置坐标；σ——标准差。

直接对高斯函数进行拟合较为困难，不妨对式（6）两边同时取对数，将其变换为如式（7）所示形如y=Ax2+Bx+C 的二次曲线来简化计算

其中抛物线顶点所在的横坐标值为

利用最小二乘法得到二次曲线的系数，即找到使函数均方误差最小的系数A、B 和C，对于拟合点坐标（xi，lnyi），均方误差表达式为

3 Taubin 法拟合圆

圆拟合问题根据其实际解决方案可大致分为2类：（1）几何拟合：使数据点到圆的几何（正交）距离最小；（2）代数拟合：使其他代数表达式达到最小化。而由于基于几何拟合的方法通常是迭代的，且其迭代准确性受初始值的影响较大，这就导致运算时间势必较长。而代数拟合方法凭借其非迭代的特点，在检测中能够实现更好的实时性，且能够避免初值选取不当造成的拟合偏差。此外，根据Chernov[14]的误差分析证明，经过仔细设计的代数拟合法（如Taubin 算法）可以在统计学上实现和几何拟合法几乎一致的精度。因此，本文中选用Taubin 法进行圆拟合。

代数法中主要是基于圆方程的代数形式

区别于其他代数方法，Taubin 法对该方程设置的约束条件为

故有Taubin 法的能量函数为

使能量函数最小化即可得到的最优解，本文中采用Levenberg-Marquardt 法进行最优化求解。最后，通过圆方程的几何参数与代数参数的转换：，即可求得拟合圆的圆心和半径。

4 实验结果与分析

4.1 实验环境

本文的边缘尺寸测量系统实验是在MATLAB R2019a 环境下实现的。借助MATLAB 实现仿真图片的生成，真实图像则通过搭建机器视觉采集系统完成采集。本文搭建的采集系统由光学平台、支架、背光板、CMOS 工业相机、计算机等组成，如图5所示。其中，相机选用大恒ME2P-1840-6GC-P 工业相机，分辨率为4 508×4 096，像元尺寸2.5μm，帧率为6.4。镜头配备大恒HN-1624-20M-C1/1X，焦距为16 mm，畸变＜0.1%。

图5 测量平台Fig.5 Measurement platform

4.2 实验测量与分析

由MATLAB 合成的仿真圆孔型零件图如图6所示。图6 表示了不同半径的圆（圆内强度为0，圆外强度为255），分别对其添加标准差为0.01～0.1共10 个不同程度的高斯白噪声，检测不同半径、不同噪声条件下的圆心位置和半径。

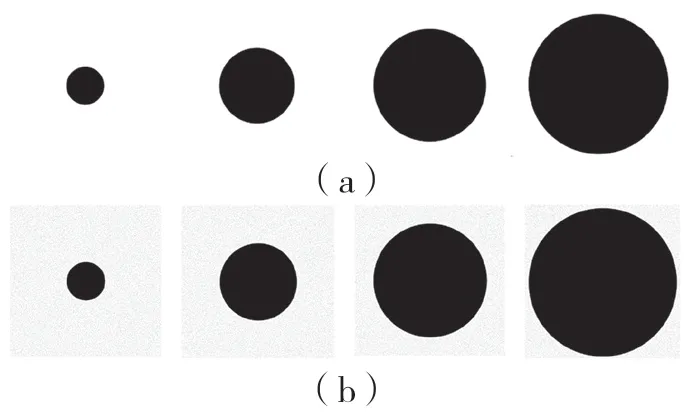
图6 仿真孔型图Fig.6 Simulated hole diagram

图7 和图8 为仿真圆孔型零件在不同半径和噪声条件下不同方法检测误差对比。可以看出，传统Canny 在与Zernike 矩结合进行测量时，针对较小内径的圆测量表现较差，在半径50 像素的圆测量中误差可达0.27 个像素，而与插值法结合则在圆心位置检测的准确度上明显劣于其他方法。利用本文提出的检测方法，对仿真图像的圆孔半径检测误差基本控制在0.01 个像素之内，而对圆心的定位检测在准确度和稳定性上均优于其他2 种方法。

图7 不同方法对圆孔半径的检测误差比较Fig.7 Comparison of positioning errors of hole detection with various methods

图8 不同方法对于孔圆心定位误差的比较Fig.8 Comparison of positioning errors of hole center detection with various methods

在对实际图像进行尺寸测量前，需要对当前视觉系统进行标定，找到像素与实际尺寸之间的转换关系，即确定标定系数。本文选择在背光环境下对内径环规进行尺寸测量，得到标定系数q，即1 像素对于实际尺寸的定标结果。

分别以圆形标定板和内径环规等作为不同大小的圆形样本，模拟孔类尺寸的测量，得到实际尺寸与误差，实验结果如表1 所示。

表1 部分圆孔样本检测结果Tab.1 Detection results of part of the hole samples

实验结果表明，本文方法对于直径7.5 mm 的圆孔类样本测量误差在0.003 mm 以内，平均相对误差为0.028%，对于直径12 mm 的孔类样本测量误差在0.015 mm 以内，平均相对误差为0.075%，而对较大尺寸孔径如40 mm 的样本测量误差则控制在0.05 mm 以内，平均相对误差为0.080%。由表1 可以看出，本文提出的测量方法在小直径样本尺寸测量上相较于传统Canny 与亚像素边缘检测结合的测量方法精度有显著提升，随着样本尺寸增大，精度差距有所降低，但仍存在一定优势。由此可见，本文提出的测量系统可以实现针对圆孔类尺寸的高精度测量。

5 结论

为了适应工业环境，本文设计了一套基于机器视觉的圆孔类尺寸精确测量方法，既保证了测量精度，又避免了人工检测精度低、效率低、易损伤加工表面等传统检测方法的固有缺点。实验结果显示，本文提出的测量方法相较于传统Canny 与亚像素边缘检测结合的测量方法实现了更高的检测精度与更好的稳定性。在仿真图片中，误差小于0.01个像素；对不同尺寸的样本真实图片平均相对误差小于0.080%；在小直径样本中表现最优，孔径误差在0.003 mm 以内；由于较大孔径的样本受镜头畸变影响更大，故测量误差相对较大，最大相对误差为0.123%。

该系统目前仅对背光环境下的圆孔类尺寸适用性最佳，如何克服不同光照方向导致的表面纹理和污染等噪声对测量带来的影响仍需进一步研究和完善。另一方面，对于相机镜头畸变的矫正问题也是下一步研究中需要考虑的问题。在接下来的研究中将着重改进上述问题，并对测量系统的适用性和鲁棒性加以改进和提高。