转角脉冲试验中横摆角速度误差注入与模拟

邹安帮，李鹏，吴婷婷，熊威

（210037 江苏省 南京市 南京林业大学 汽车与交通工程学院）

0 引言

随着计算机技术的发展，虚拟样机技术在汽车试验中得到广泛应用，如ADAMS、CarSim 等[1]。虚拟样机技术通过车辆动力学模型进行仿真，可以仿真车辆对驾驶员、路面及空气动力学输入的响应，也可用来预测和仿真汽车整车的操纵稳定性、制动性、平顺性、动力性和经济性等试验。

虚拟样机中动力学模型输出的数据是理想化的，不存在传感器等设备的误差，而在实车试验测量中，由于外界条件、仪器设备等因素的影响，测量所得到的的数值与被测参数的真实值之间总会有所不同，二者之间存在误差。目前有关动力学模型输出数据注入误差的文献较少，多为针对提升测量单元的精度进行传感器的标定和补偿。如贾浩男等[2]分析MEMS 惯性测量单元的误差原理以提高MEMS-IMU 传感器精度，建立微陀螺仪和微加速度计的误差模型，并对其进行标定和补偿实验来提高导航与定位的精度；马亚平等[3]针对传统的正交补偿方法难以保证惯性测量单元具有较高正交补偿精度的问题，提出了一种改进的适用于大角度和小角度安装误差角情形的正交补偿方法；杨莉等[4]对惯性传感器的误差来源进行了分析，建立了精简后向传播神经网络来表征环境温度、机械安装误差、机械振动与电磁干扰因素对误差的影响模型，并利用该方法对惯性传感器误差进行了标定。

为了使操纵稳定性试验数据接近实车试验数据，本文采用ADAMS/Car 软件建立整车模型进行操纵稳定性中的转角脉冲试验，建立传感器误差模型，对试验数据进行误差注入与模拟。

1 整车模型的建立

在ADAMS 中搭建一个完整的车辆模型，需要包括车辆的车轮、悬架、转向以及车身子系统[2]。ADAMS/Car 仿真软件自带各个系统的模板，在模板的基础上加上各系统的属性文件，最后装配组合成整车模型[3]。整车建模的顺序如图1 所示。ADAMS/Car 仿真软件中的整车模型如图2 所示。

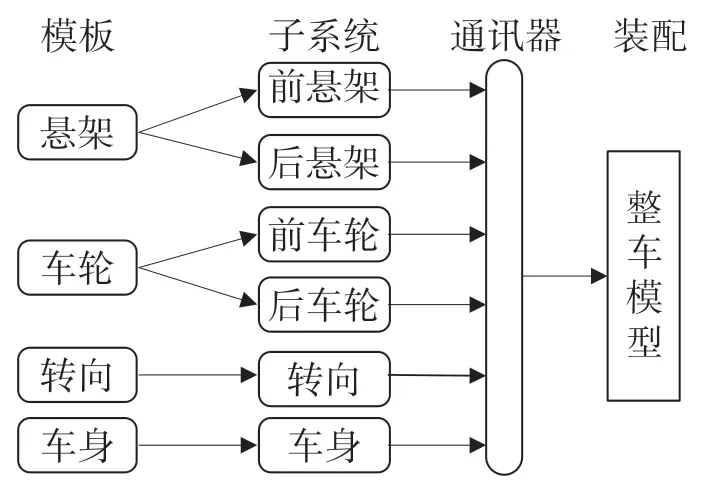
图1 整车模型的建立过程Fig.1 The process of building vehicle model

图2 ADAMS/Car 中的整车模型Fig.2 Full vehicle model in ADAMS/Car

2 误差理论简介

在所有的测量环节中，由于仪器自身原因和外界影响都会影响测量数据的准确性，被测量参数的真实值会和测量值有一定的偏差，即测量误差。测量误差可分为以下3 类。

（1）系统误差。系统误差可分为固定系统误差和变化系统误差。变化系统误差会具有一定的规律性，如累进系统误差为每次测量都成倍增加或减少一个固定误差。比如，测量仪器在制造时，指针没有精确指在零位；加速度传感器设计时3 个轴没有正交产生的误差，此时加速度传感器每个轴都会有一个零漂值。

（2）随机误差。在相同条件下，对同一个被测参数进行多次重复性测量，可能会得到不完全相同的测量数据，得到的测量数据存在的误差在数值和符号方面可能各不相同，这些误差称为随机误差。随机误差是由于一些因素产生细微变化时对测量数据产生的影响，且这些因素相互独立。如电阻产生感应信号的传感器会因为环境温度的细微波动产生误差。随机误差由于影响因素相互独立，且没有规律性，所以对于个体的随机误差没有规律且无法避免，但是对于总体而言，随机误差在测量次数达到一定程度后会服从正态分布的统计学规律[4]。

（3）过失误差。造成过失误差的原因可能是在测量工作时疏忽大意或者错误使用仪器。随着目前科学技术的进步，传感器多是带有数字输出功能，不会出现操作错误和疏忽大意的情况，所以过失误差不再过多讨论。

3 陀螺仪误差模型

陀螺仪的基本原理为：在经典哥氏惯性力理论的基础上，利用哥氏效应得到角速度值。陀螺仪产生的误差主要分为系统误差和随机误差。

3.1 陀螺仪系统误差

陀螺仪的系统误差主要有零偏与标度因素误差、安装误差以及比力有关项误差[5]。

（1）零偏与标度因素误差。由于传感器内部器件会有干扰力矩，相应产生的误差即为传感器的零偏误差。当传感器零输入时，对其进行多次测量，求得输出值的平均值即为零偏值。在陀螺仪的量程内，对输入和输出值进行拟合，传感器的输出值与输入值的斜率偏差即为标度因素。标度因素包括标度因素的重复性、非线性、不对称性等多项指标[6]。

（2）安装误差。指传感器中各元件安装时会产生安装误差角，主要是由于六面体安装不正交引起的。

（3）比力有关项误差。主要成因有两方面：①由于本身原理以及工艺不完善；②由于过载的角运动等力学因素[7]。所以由力学引起的误差均为比力有关项误差。

由以上系统误差的组成得到陀螺仪的系统误差模型为

式中：ωtx，ωty，ωtz——轴陀螺仪输出值，(°)/s；ωx0，ωy0，ωz0——轴陀螺仪的零偏漂移值，(°)/s；Sgx，Sgy，Sgz——轴陀螺仪的标度因素；δij——i 轴偏向j 轴的安装误差系数；ωlx，ωly，ωlz——陀螺仪输入值(°)/s；dij——i 轴陀螺仪输出与向j 轴比力有关系数，即与g有关项；ax，ay，az——各轴非引力加速度。

3.2 陀螺仪随机误差

陀螺仪在车载运动时，处于振动状态，传统的误差分析方法无法分析出误差的种类、幅值和比重等信息。本文采用Allen 方差分析法来确定误差的类型、大小和比重，并据此建立陀螺仪的随机误差模型。

Allen 方差分析的各种误差源如图3 所示，特征参数指标如表1 所示。不同指标对应不同的斜率。

表1 Allan 标准差分析曲线中各种误差源Tab.1 Various error sources in collimation analysis curves

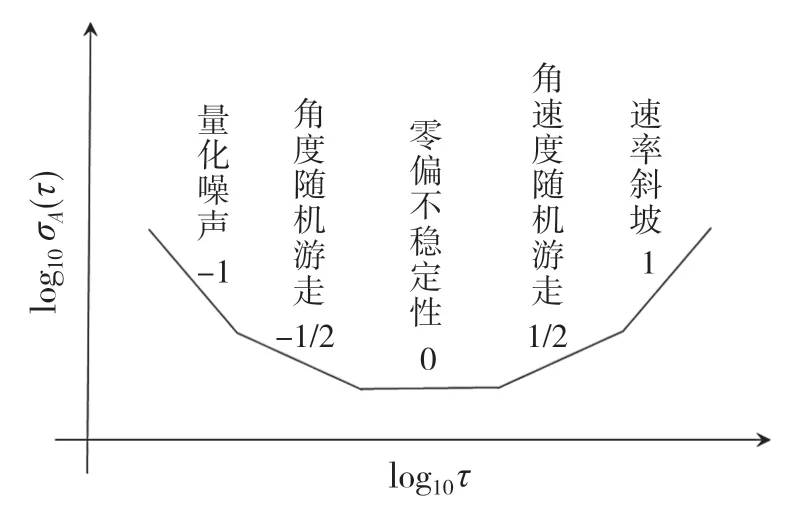
图3 曲线斜率与误差成分关系Fig.3 Relation between curve slope and error component

则陀螺仪的Allen 方差为

式中：σQ——量化噪声标准误差；σN——随机游走标准误差；σB——零偏不稳定性标准误差；σK——速率随机游走标准误差；σR——速率斜坡标准误差。

4 陀螺仪误差注入与模拟

由于转角脉冲试验中需要对横摆角速度进行测量，而横摆角速度由陀螺仪的Z 轴测量得到，且陀螺仪包含系统误差和随机误差，可得陀螺仪误差注入模型为

式中：ωt——加入误差后输出值；ω0——动力学模型输出值；fω——系统误差；Δω——随机误差；ωi=ω0+fω——动力学模型输出值与系统误差的和。

陀螺仪误差模型的系数可根据具体传感器标定系数进行设置，误差模型系数如表2 和表3 所示。

表2 陀螺仪与g 有关项系数Tab.2 Coefficients of gyroscope and g-related term

表3 陀螺仪的系统误差模型系数Tab.3 Systematic error model coefficients of gyroscope

则陀螺仪的系统误差模型为

将式（4）和陀螺仪Z 轴Allen 方差带入式（3）得

式中：ωlx，ωly，ωlz——动力学模型中3 个方向的角速度输出值；ax，ay，az——各轴非引力加速度；Δω——服从均值是0、方差是σωtotal的正态分布随机数，由MATLAB 中normrnd()函数生成。

设置的陀螺仪传感器的Allen 方差如表4 所示。

表4 陀螺仪Allen 方差Tab.4 Gyroscope Allen variance

由式（2）可得陀螺仪的横摆角速度（Z 轴）随机误差的方差为σωtotal=0.073 376°。

4.1 陀螺仪误差注入实例

本文针对转向盘转角脉冲试验得到的横摆角速度进行误差注入与模拟。采用GB/T 6323-2014《汽车操纵稳定性试验方法》[8]进行试验，本文车辆模型设计最高车速为174.2 km/h，则试验车速为V=174.2×70%=120 km/h；方向盘转角脉宽输入为0.5 s；最大转角需使侧向加速度达到4 m/s2。

通过试验得到的侧向加速度随时间变化曲线如图4 所示，表明本次试验符合国家标准规定的试验工况。根据陀螺仪误差模型式（5）可知，比力有关项还需要输出纵向加速度和垂向加速度，如图5 和图6 所示。

图4 侧向加速度随时间变化曲线Fig.4 Curve of lateral acceleration with time

图5 纵向加速度随时间变化曲线Fig.5 Curve of longitudinal acceleration with time

图6 垂向加速度随时间变化曲线Fig.6 Curve of vertical acceleration with time

根据陀螺仪误差模型式（5）可知，还需要动力学模型中三个方向的陀螺仪输出值。转角脉冲试验三个方向的角速度随时间变化曲线如图7、图8、图9 所示。

图7 横摆角速度随时间变化曲线Fig.7 Curve of yaw angular velocity with time

图8 侧倾角速度随时间变化曲线Fig.8 Curve of roll angular velocity with time

图9 俯仰角速度随时间变化曲线Fig.9 Curve of pitch angular velocity with time

根据陀螺仪误差注入模型即式（5），通过误差计算并对注入误差后的横摆角速度进行模拟，可得到注入误差后的横摆角速度随时间变化的曲线如图10 所示。

图10 横摆角速度随时间变化曲线Fig.10 Curve of yaw angular velocity with time

4.2 误差注入验证

判断误差时，测量数据需满足一定的数量要求，所以在原试验基础上再进行9 次转角脉冲试验，提取所有试验的横摆角速度峰值，如表5 所示。由表5 测量数据可得正态分布概率图如图11 所示。使用MATLAB 中lillietest()函数对数据进行正态分布检验，lillietest()函数返回值H 为假设,只有0 和1 两种情况，H=0 假设符合正态分布，H=1 假设不符合正态分布。返回值P 为方差概率，即事情的发生概率：P<0.05 为不可能事件，拒绝假设；P>0.05，接受假设。对表5 中的数据进行正态分布检验返回结果H=0，P=0.211 5>0.05，表示其符合正态分布。说明存在随机误差。

表5 10 次试验的横摆角速度峰值Tab.5 Peak yaw rate for 10 trials

图11 正态分布概率图Fig.11 Normal distribution probability plot

为了检验传感器的系统误差，需要改变试验条件，即对陀螺仪的系统误差系数重新设置。重新设置的系统误差系数如表6、表7 所示。

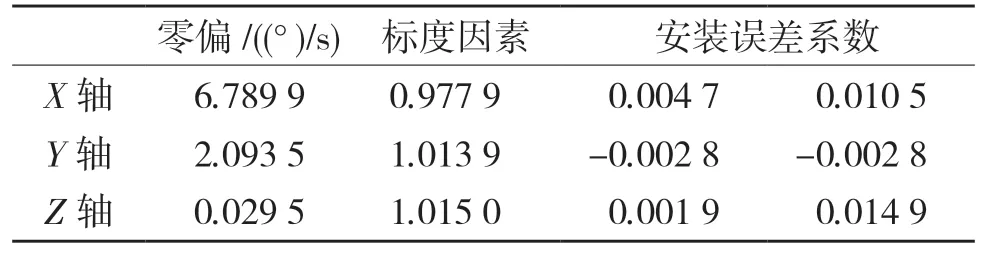
表6 重新设置后陀螺仪系统误差系数Tab.6 Error coefficient of gyroscope system after reset

表7 重新设置后陀螺仪与g 有关项系数Tab.7 Coefficients of gyroscope and g-related term after reset

根据式（1）可得到重新安装后的陀螺仪误差模型为

式中：Δω——服从均值是0、方差是σωtotal=0.073 376 °的正态分布随机数；其余变量含义与式（5）相同。

将重新设置系统误差系数的误差模型进行转角阶跃试验10次，提取横摆角速度峰值如表8所示。

表8 陀螺仪重新设置后注入误差后的横摆角速度峰值Tab.8 Peak yaw rate after injecting error after gyro remount

由表8 数据可得正态分布概率图，如图12所示，数据符合正态分布，且使用MATLAB 中lillietest()函数对数据进行正态分布检验，返回结果H=0，P=0.145 8>0.05，表示其符合正态分布，说明存在随机误差。

图12 重新设置后横摆角速度峰值正态分布概率图Fig.12 Probability map of normal distribution of peak yaw rate after reset

将表5 和表8 中的数据绘制于一张正态分布概率图，如图13 所示。由图13 可知，数据不符合正态分布，且使用MATLAB 中lillietest()函数对数据进行正态分布检验，返回结果H=1，表示其不符合正态分布。

图13 正态分布概率图Fig.13 Normal distribution probability plot

根据分布检验法，若随机误差服从正态分布，则包含随机误差的测量值也服从正态分布。所以，测量列若服从正态分布，则测量列含有随机误差，反之，若测量列不服从正态分布，则有理由怀疑测量列中含有系统误差[9]。

综上，根据分布检验法，重新设置系统误差系数前后的数据分别符合正态分布，表明其各含有随机误差，而重新设置系统误差系数前后所有测量数据不服从正态分布，则表明陀螺仪含有系统误差。由上文可知给陀螺仪注入了系统误差和随机误差，与误差判别的结论一致，所以传感器误差模型与误差注入方法可行。

5 结语

（1）本文根据陀螺仪传感器的构造与误差产生机理，对陀螺仪系统误差和随机误差的数学特性进行分析，建立了相应的误差模型。

（2）本文提出一种随机误差注入方法，对车辆动力学模型输出的横摆角速度数据进行误差注入模拟，由分布检验法验证了误差注入方法的有效性。

（3）本研究存在一定的局限性，由于传感器需要经过实验标定才能确定误差的具体数值，所以本文验证方法只能确定误差的类型。