基于ANSYS 的汽车传动轴模态识别

陈美宏，徐传燕，许春晓，李光胜

（250357 山东省 济南市 山东交通学院 汽车工程学院）

0 引言

弯曲振动和扭转振动是目前传动轴动平衡研究的两个主要方面。当传动轴工作时，假如自身固有频率与外部激励的频率相近时就会产生共振现象，整个传动系统将发生弯曲振动[1]。扭转振动的研究当前仍以理论计算为主。随着有限元方法的兴起，利用有限元仿真解决传动轴振动问题的应用也越来越多。Righettini 等[2]提出了一种有限元分析的计算方法，得到了简化的有限元模型；张立军等[3]从激励—传递路径—响应的分析角度，探讨了十字轴万向节激励、传递路径和传动轴激励的响应等三方面的解决方案；谢亮亮等[4]对传动轴模型进行简化并多次利用Workbench 仿真软件进行仿真得出重要模态参数，在此基础上运用MATLAB 进行优化设计，提高了传动轴的临界转速，使传动轴的设计得到了优化。上述研究虽取得很大进展，但多为仿真，未通过具体试验测试验证其结果的可靠性。

本文首先基于ANSYS 软件对传动轴进行有限元模态仿真，得出固有频率和振型等动态参数，进而通过LMS SCADAS 数据采集器利用锤击法对传动轴进行试验模态分析，测试传动轴传递函数，提取其固有频率和主振型，从而验证有限元分析结果的正确性。避开传动轴工作过程中出现共振现象，从而达到减振降噪的作用[5]。而且为选择合适的材料来满足传动轴工作时的强度、刚度要求提供可靠数据。

1 有限元模态分析

1.1 模型建立

本实验采用间接建模的方式，利用卷尺、直尺、游标卡尺等测量工具，测得传动轴中间轴管的大径是75 mm、中间轴管的总长315 mm 等尺寸，传动轴中间是封闭的壳体，无法测具体厚度，查阅有关资料知其厚度为1.5～3.0 mm。为方便建模，忽略传动轴表面局部凹坑和凸起部分，采用三维设计软件UG 建立三维实体模型[6]。传动轴实体和三维模型如图1 所示。

图1 传动轴Fig.1 Transmission shaft

在有限元分析软件ANSYS 中，设置传动轴参数并进行网格划分。选择尺寸长度为0.005 m 的三角形单元，共划分15 526 个单元，包括58 946 个节点，如图2 所示。通过查阅有关资料定义传动轴的材料属性如表1 所示。

表1 传动轴材料属性Tab.1 Material properties of drive shaft

图2 传动轴网格划分Fig.2 Transmission shaft grid division

1.2 有限元结果分析

边界条件设为自由边界，进行自由模态分析计算。得到传动轴自由模态前12 阶最大位移和固有频率如表2 所示。自由模态分析前6 阶为刚体模态，从表2 可以看出模态分析结果中的前6 阶振型固有频率接近于0，因此非刚体模态分析结果应从第7 阶开始计算[7]。相邻两阶7 和8 阶、9 和10 阶、11 和12 阶固有频率值大致相等，说明它们是系统振动方程的重根，对应振型相同，相位不同。传动轴前4 阶自由模态振型如图3 所示。

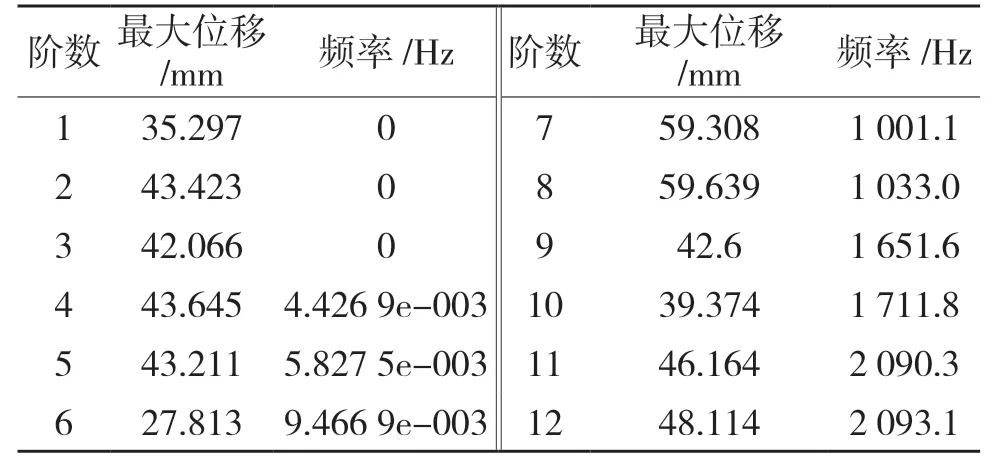
表2 传动轴自由模态下前12 阶最大位移及固有频率Tab.2 Maximum displacement and natural frequency of the first 12 orders under free mode of transmission shaft

图3 传动轴前4 阶自由模态振型Fig.3 The first four free mode shapes of transmission shaft

有限元分析中，传动轴的第1 阶和第2 阶振型为膨胀，第3 阶和第4 阶振型为弯曲，第5 阶和第6 阶振型仍为膨胀[8-9]。由于在实际中传动轴的主要破坏形式是弯曲，故本文主要分析传动轴第1 阶和第2 阶弯曲变形的振型和固有频率，即有限元分析的第9 阶和第10 阶结果。如图4 所示。表3 为传动轴第1 阶、第2 阶弯曲变形振型和固有频率。

表3 传动轴两阶弯曲变形振型和固有频率Tab.3 Vibration mode and natural frequency of two-order bending deformation of transmission shaft

图4 传动轴两阶弯曲变形振型Fig.4 Vibration mode of transmission shaft two-order bending deformation

2 试验模态分析

2.1 试验设置

采用锤击测试法对传动轴进行试验模态分析[10]。模态试验所用仪器如表4 所示。

表4 模态试验仪器Tab.4 Modal test instruments

传动轴测点位置选择及传感器布置应能完整反映待测构件的基本外形和特征，合理安排试件测点的位置和数量，对提高模态参数的精度有着重要的影响。高频模态的振型驻波波长相对较短，为了更好地描述这些模态，需要更多的测点[11]。综合考虑以上因素，沿传动轴布置54 个测点，主要位于传动轴中间的壳体部分，从1～54 开始标记，线框图如图5 所示，布置3 个加速度传感器，分别位于测点18、29、38 处，将传感器贴附于传动轴，为测量传动轴自由状态下的模态参数，用有弹性的绳子将传动轴竖直悬置固定在架子上，如图6 所示。

图5 传动轴线框图Fig.5 Block diagram of transmission axis

图6 支承的传动轴Fig.6 Supporting drive shaft

在LMS Test.Lab 软件中设置通道、锤击示波以及量程，根据力锤敲击力选择合适的带宽。为提高激励信号的信噪比、降低试验误差，采用5 次测量取平均值的方法，试验过程中如果出现连击和过载则数据无效，需要重新测量[12]。最后计算传动轴的频响函数（frequency response function，FRF），识别模态振型，提取固有频率。

2.2 试验结果分析

2.2.1 相干函数与频响函数

为评估试验有效性，选取第38 测点+y 方向响应第29 测点+x 方向激励的相干函数与FRF，如图7 所示。相干系数取0～1，该系数越接近于1，说明输出完全由输入引起。由图7（a）可知：相干系数接近于1，说明图7（b）中FRF 有效，结构的响应完全由激励引起，并充分激起了传动轴两阶模态频率范围内的模态。

图7 第38 测点+y 方向响应、第29 测点+x 方向激励的相干函数与FRFFig.7 Coherence function and FRF of the response of the 38th measurement point +y direction to the excitation of the 29th measurement point +x direction

试验所得稳态图如图8 所示，图8 中o，f，d，v，s 的含义如表5 所示。稳态图是从测量数据中提取极点的有效工具，随着参与拟合的模态阶数增加，稳态图中出现系统极点，即稳点的s 列，极点位置代表1 阶模态，由此来确认模态阶数[13-14]。

表5 模态极点的符号及意义Tab.5 Symbolic meaning of modal poles

图8 稳态图Fig.8 Steady state diagram

2.2.2 固有频率与模态振型

在LMS Test.Lab 软件的Poly MAX 模块提取传动轴的固有频率和模态振型。试验得到的模态阵型如图9 所示。由图9 可知：传动轴两阶试验模态振型与图4 传动轴两阶弯曲变形振型基本一致，验证了有限元分析结果的准确性。试验模态与有限元模态固有频率对比如表6 所示。

表6 试验模态与有限元模态固有频率对比Tab.6 Comparison of natural frequencies between experimental modes and finite element modes

图9 1～2 阶试验模态振型Fig.9 Experimental mode shapes of order 1～2

由表6 可知，有限元模态分析数据和试验模态分析数据的最小相对误差为0.73%，最大相对误差为2.6%，最大相对误差未超过5%，在可接受误差范围内。造成误差的原因有以下几个方面:（1）尺寸误差，由于采用卷尺人工测量尺寸以及不确定传动轴内壁厚度，查阅资料估计建模，精度不够，导致尺寸存在一定误差；（2）几何建模时，省略倒角和圆孔等产生的误差；（3）有限元软件ANSYS中构件的材料较为理想，而实验对象的材料不均匀，导致建模的密度、弹性模量与实际有差别；（4）试验环境条件对传感器的影响。

2.3 试验模态验证

验证所得模态结果的正确性，可采用不涉及数学工具的直观检验。由于测点位置得到的每阶模态参数有偏差，需要通过曲线拟合获得更精确的模态参数，绘制拟合FRF 曲线与实测FRF 曲线进行对比，验证试验所得模态结果。在LMS 软件的Poly MAX 模块下进行模态提取，根据获取的模态参数对某个测点进行FRF 拟合，如图10 所示。

图10 拟合FRF 与实测FRFFig.10 Fitted FRF and measured FRF

对各阶模态进行模态置信度分析，检验模态质量，如图11 所示。模态置信度表示任意2 个模态振型向量几何上的相关性，取值为0～100%，如果模态置信度接近0，则2 个振型向量之间相关性很小，或者是正交的。由图11 可知，试验所得各阶模态相关性都比较低，基本在9%以下，不存在明显的线性关系，表明模态振型的独立性较好。

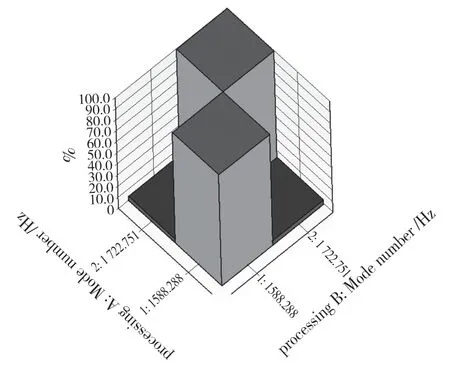
图11 试验模态置信度柱状图Fig.11 Histogram of test modal confidence

3 结论

本文采用有限元分析法与试验模态测试法，分别得到传动轴固有频率与振型并进行对比，验证了有限元结果的准确性。主要结论如下：

（1）运用ANSYS 建立传动轴实体模型，进行有限元模态分析，计算出传动轴两阶弯曲变形的模态振型和固有频率；（2）采用锤击法对传动轴进行试验模态测试，测出其传递函数，并提取传动轴两阶弯曲变形的模态参数及固有频率；（3）对比有限元模态仿真和试验模态分析结果，得出传动轴两阶弯曲变形的固有频率误差在5%以内，2 阶振型基本一致，验证了有限元分析结果的正确性。

研究结果可为传动轴结构优化、材料更新以及提高汽车NVH 性能提供参考。由于尺寸测量、建模简化、试验对象材料不均匀、试验环境误差以及操作不当等因素影响，试验结果与真实值存在着一定误差。后续研究还可以进一步改变传动轴的壁，厚、传动轴的材料属性、结构刚度、质量，计算分析传动轴的固有频率和振型，为传动轴设计时避免共振的发生提供更多参考，从而节约人力和物力。