基于模型预测控制的无人驾驶主动避障策略

崔玉定，熊豪杰，贺满川，薛仁强

（430065 湖北省 武汉市 武汉科技大学 汽车与交通工程学院）

0 引言

无人驾驶是汽车技术发展的重要趋势之一，可以降低交通事故的发生率，减少拥堵现象，同时能提高资源的利用率。其中主动避障技术作为无人驾驶的关键受到广泛的研究。

主动避障技术主要涵盖了局部路径规划和轨迹跟踪。局部路径规划主要的控制目标是在已知环境模型中，从当前位置到目标点间寻找一条可行的无碰撞路径[1]。目前常用的算法有人工势场法、基于搜索的轨迹优化算法和图窗搜索法等[2]。人工势场法是一种虚拟力法，由Khatib[3]最早提出并应用于路径规划，规划出的路径相对平滑，算法简单可靠，实时性较好。但传统人工势场法也存在容易陷入局部最优和目标不可达的问题。安林芳等[4]通过在斥力场中加入虚拟目标点，避免了目标点不可达问题的发生。修彩靖等[5]改变了传统的引力场目标函数构建方式，建立高斯组合隶属函数，并在其中加入了调节因子，消除了传统人工势场法容易出现局部最优的问题。在轨迹跟踪控制方面，Tagne 等[6]采用滑模控制算法，以实际轨迹与参考轨迹的侧向偏差为基础设计滑动面，实现对目标轨迹的跟踪。虽然该方法鲁棒性较好，但会引起严重的系统抖振，系统稳定性较差。Fan 等[7]利用 LQR控制算法对线性化后的车辆系统进行闭环控制，最终设计的控制系统具有稳定性高和实时性好的优点，但跟踪过程中出现了较大的偏差且LQR 算法无法对状态量和控制量加以限制处理约束问题。

基于模型预测控制（MPC）设计了分层式主动转向避障控制器。在上层避障轨迹规划层，接收传感器传入的障碍物信息和全局期望路径信息，为避开障碍物引入了避障惩罚函数并在目标函数中考虑了车辆运动学约束，规划出一条无碰撞的局部路径。下层轨迹跟踪控制层接收上层规划器传来的局部参考轨迹信息，将车辆安全行驶包络线约束与模型预测控制算法相结合，求解出前轮转向角的最优解[8]。

1 局部路径规划控制器

1.1 车辆点质量模型

为减小计算量、提高计算速度同时兼顾控制性能，选用车辆点质量模型，该模型将车辆看作一个质量点，忽略车身尺寸、轮胎受力和载荷变化[9]，如图1 所示。图1 中：O——车辆质心；x——车辆纵向位移；——车辆纵向速度；y——车辆侧向位移；——车辆侧向速度；φ——车辆横摆角。

图1 车辆点质量模型Fig.1 Point mass model of autonomous vehicle

在大地参考坐标系下，车辆点质量模型表示为

1.2 规划层预测模型

路径重规划层的实时性要求较低，且采用的点质量模型也有一定程度的简化。采用非线性模型预测控制算法（NMPC）在满足轨迹重规划的要求外具有更高的求解精度，对于后续的二次规划求解函数的设计也带来了便利。

采用欧拉法对点质量模型进行离散化，得到车辆点质量模型的差分方程

在小学生的成长过程中，家庭教育不可或缺，家庭也应该对学校的教学起监督作用。但是在调查中发现，出于对学生成绩的考虑，部分家长并不关心教学改革，也不关心多媒体在教学中的应用，只关心学生的成绩是否优秀，如果学生的成绩得到了提升，就会对教师和学校给予高度的评价，反之则评价较低。这在无形之中对于教师形成的压力，也在一定程度上阻碍了教学改革、教学创新。

式中：k——当前采样时刻；T——离散时间；y（k），x（k）——车辆在k 时刻横、纵向位移；——车辆在k 时刻的横、纵向速度；φ（k）——车辆在k 时刻的横摆角。

为简化计算，假设车辆纵向速度为一恒定常数，即纵向加速度ax=0,以汽车横向加速度为控制变量即u=ay，以为状态变量，将式（2）整理为

式中：i=1，2，…，Np，j=1，2，…，Nc；f（·）——点质量模型的差分方程函数表达式；Np——预测时域；Nc——控制时域；t——采样时间。

式中：Jobs——具体的惩罚函数值；Sobs——权重系数；（xi，yi）——障碍物第i 个端点在大地坐标系下的位置坐标；（xo，yo）——车辆质心坐标；κ——一个极小的非0 正数，目的是防止惩罚函数的分母为0。

1.3 优化问题构建与求解

为使智能车辆准确高效跟踪上层控制器规划的局部轨迹，需考虑车辆纵向、侧向和横摆3 个维度的运动，建立更加精确的车辆动力学模型。如图2 所示，图2 中：m——整车质量；Iz——车辆绕Z轴转动惯量；Fxf，Fyr——车辆前后轮胎所受到的侧偏力；Fxf，Fxr——前后轮胎受到的纵向力。

小学科学的最终目标应当是促使学生能够主动将科学技能与生活实践联系起来，进而实现科学教学内容的生活化以及学生课外活动的生活化。达到这一最终目标，除了需要科学教师自身拥有超高的专业素养，还需要其主动将教学内容与学生生活实际有机结合起来，运用科学的引导作用，促使学生将科学知识运用到课外的实践活动中，帮助学生理解科学与生活的密切联系性，为生活服务。

为躲避行驶路径上的障碍物，需要在上层控制器的目标函数中加入避障惩罚函数。龚建伟等[10]提出根据障碍物点与目标点之间的距离偏差和车辆行驶速度设置障碍物惩罚系数，当车辆与障碍物越近、车速越高，惩罚值越大。具体惩罚功能函数为

式中，f(x,y)为回波信号函数, Xc为脉冲波形形心的时间位置.用式(1)对脉冲激光波形建模，激光雷达形心算法基于式(3)计算形心，为了降低信号中噪声对形心计算的影响，在对采样点进行滤波预处理后，通过滑窗找到波形位置，根据形心计算理论分别计算发射波的形心位置xf和回波的形心位置xr，距离信息的计算公式为

根据式（3）可得NMPC 控制时域内的预测表达式为

（x）通过加权集结算子将子组Ey（y=1，2，…，10）群决策矩阵y=1，2，…，10）转化为组E群决策矩阵D=（dij）m×n（i1，2，...，10，j=1，2，3，4，y=1，2，…，10）。

1.3.2 轨迹重规划层目标函数设计

将线性化后的Pacejka 轮胎模型引入车辆动力学模型中得到

利用式（16）和式（17）进行迭代运算，可以得到预测时域内系统输出量表达式为

式中：Yref——预先给定的全局参考轨迹；Q——上层控制器中的输出权重系数矩阵；R——控制输入的权重系数矩阵；Jobs——避障惩罚函数值。

1.4 重规划轨迹拟合

在轨迹重规划算法中，重规划后的轨迹是离散点的形式。如果直接以离散点的形式传输给下层控制器，会占用太多的控制器输出与输入接口，控制器的设计会变得更加复杂[11]。此外由于多个控制周期的轨迹可以包含在规划控制器的一次求解范围内，因此上层规划周期与下层控制周期并不相同。为了确保上层局部规划控制器与下层跟踪控制器之间的顺利对接，采用5 次多项式拟合重规划后的离散轨迹点，形式为

式中：ai，bi（i=0，1，2，3，4，5）——待求轨迹拟合和航向角拟合参数。

2 轨迹跟踪控制器

2.1 车辆动力学模型

1.3.1 避障惩罚函数设计

图2 车辆动力学模型Fig.2 Dynamic model of autonomous vehicle

本文只涉及转向避障控制，车辆纵向速度被设定为常数，只考虑侧向和横摆2 个维度的运动，根据车辆受力平衡和力矩平衡可以得到：

第Ⅲ含矿带赋存于石闫背斜南翼，位于第Ⅱ含矿带以南，以东石门断层为界可分为东西两个区段，东段为石门铁矿黄牛岭铁矿区，向东至白水牛石断层，控制长度约2.4km，矿带核部被剥蚀，矿带倾向SW，S，倾角45°～65°。矿带发育2个矿层，矿层总厚度在13.45～14.94m之间，厚度稳定；西段为中钢山东矿业小闫庄铁矿区南翼，为隐伏矿床，发育核部，与第Ⅱ含矿带在核部相连，矿带倾角由上至下由缓变陡，控制长度约2.6km，向西尚无工程控制，矿带发育3个体，矿体总厚度23.50m，厚度稳定。

基于小角度假设，选用线性化的魔术轮胎模型[12]。具体计算公式为

式中：Cα——车轮等效侧偏刚度；Cs——车轮纵向刚度；α——轮胎侧偏角；S——轮胎滑移率。

重规划后的轨迹应满足：（1）能避开障碍物，满足安全避障要求；（2）车辆的运动学及性能约束；（3）与全局参考路径之间的偏差足够小。因此设计的轨迹重规划层的目标函数为

可改写为如式（12）、式（13）的形式

在生活质量评分方面，观察组显著优于对照组（P＜0.05）；在肢体功能评分情况方面，观察组较对照组优势显著（P＜0.05），充分表明其临床优势。

2.2 轨迹跟踪层预测模型

由于用于轨迹跟踪层的车辆三自由度模型比较复杂，且采样周期短，非线性模型预测控制不能满足实时性的要求。基于状态轨迹线性化方法对整车模型进行近似线性化，以获得线性时变模型预测控制[13]。状态轨迹线性化的基本原理是通过对车辆系统连续施加恒定的控制量来获得车辆状态轨迹，然后通过车辆状态轨迹与实际状态量之间的偏差来线性化整车模型。

假设车辆状态方程有一工作点为[χ0，u0]，在[χ0，u0]以泰勒公式展开，为提高计算速度，忽略1阶以上的高阶项，可得

得到在每一采样时间t 有

为保证车辆输入量变化平稳，所以在模型预测控制中对控制量采用增量方式，以线性时变模型当前状态量和上一采样时刻的控制量为新的状态变量，即ξ(k)=[χ(k);u(k-1)]。将线性时变模型控制量的变化量即Δu(k)作为控制变量,得到系统状态方程和系统输出方程

甘薯又名地瓜、山芋、番薯等，是旋花科一年生或多年生草本块根植物。我国是世界上最大的甘薯生产国，占世界总产量的75.3%。我们日常食用的部分，就是甘薯的块根。

目前辣椒辣度的测定方法中，国标(GB 10783-2008)法[2，3]测定辣椒碱含量，存在使用巨毒药品、重复性差等问题；Scoville感官评定法[4，5]存在测试环境限制较多、主观成分较大的问题；高效液相色谱法(High Performance Liquid Chromatography，HPLC)[6-8]的操作环境难以摸索，体系难以建立，并且仪器维护费用较高，且不便于田间应用。因此，需要建立一种便携式的快速、准确、稳定的检测技术。

2.3 轨迹跟踪层优化问题构建与求解

2.3.1 车辆安全行驶包络线约束构建

当智能车辆进行轨迹跟踪时，势必会产生横向运动，车辆容易发生失稳现象。所以一个完整的轨迹跟踪控制器，除了要满足轨迹跟踪精度要求，还要保证车辆系统的稳定。Bobier 等[14]提出车辆质心侧偏角和横摆角速度对于车辆稳定性起着非常重要的作用。车辆稳定包络线如图3 所示，只要车辆质心侧偏角和横摆角速度处于车辆横向稳定安全区域即包络线之内，就可以保证车辆稳定行驶。将车辆安全行驶包络线与模型预测控制相结合，设计出具有车辆稳定控制的轨迹跟踪控制器。

3.7 中医耳压疗法 减少或消除ICU综合征，除了上述治疗及护理外，传统的中医治疗也有一定效果。曾影红等［29］报道，对63例ICU综合征患者进行中医耳压疗法，总有效率约68.3%，且此法具有较好的疗效，无损伤、无不良反应、操作简便和经济等优点。

式中：vx——车辆纵向速度；——横摆角速度上限值；αlim——轮胎侧偏角上限值。

图3 车辆安全行驶包络线约束Fig.3 Constraints of envelope for safe driving of vehicles

需要声明的是，该模型不考虑变电站、线路的短时过载能力和转供条件下的N-1安全校验。通过该模型的应用，可以为变电站全停进行升级改造提供参考依据。

由于车辆行驶时前后轴距受荷载转移、悬架运动等影响，后轮载荷相对于前轮载荷较大，后轮的侧偏力更容易达到饱和状态，且当车辆发生横摆失稳时，后轴侧滑造成的危害更大[15]，所以安全包络线边界受后轮侧偏角决定。由魔术轮胎公式可知，后轮的最大侧偏角为

式中：μ——路面摩擦系数；l——车辆轴距；Cαr——后轮等效侧偏刚度。

为将安全包络线约束与模型预测控制相结合，可以使用一个线性不等式约束实现。同时当车辆轮胎进入非线性区域时，并不一定导致车辆侧向失稳，可以在线性不等式中加入松弛因子，对约束值进行适当的放宽，具体形式为

2.3.2 目标函数设计

在跟踪过程中，应使实际轨迹与参考轨迹偏差尽可能小，转角及转角增量应在一定的范围内，同时考虑安全行驶包络线约束，构建出优化形式的线性模型预测控制的目标函数为

式中：Yref——二次规划后的局部参考轨迹；umin——转角上下边界；Δumax，Δumin——转角增量的上下边界；ymax，ymin——系统输出的约束。

国际数学教育大会（ICME）是代表数学教育界最高水平的学术会议，也是世界各国数学教育最新进展和成果的展示、交流平台，迄今为止已召开了13届．经过中国数学教育工作者的不懈努力，华东师范大学获得2020年ICME-14的举办权，这是国际数学教育大会首次在中国举办．以此为契机，西南大学将承办ICME-14少数民族数学教育卫星会议，旨在让世界各国研究者相互交流本国民族数学教育问题，分享民族数学教育中的特色、经验，探讨民族数学教育发展的路径，目前会议正在紧锣密鼓的筹备中．

3 仿真验证

为验证提出的分层式MPC 规划控制器的可靠性，基于汽车动力学仿真软件MATLAB/Simulink和CarSim 建立联合仿真模型，设置路面附着系数为0.85，对应车辆行驶路面；设置双移线全局参考轨迹，并在双移线路段上30 m 处设一个5.0 m×0.5 m 的静止障碍物，验证车辆在低、中、高速行驶时避障的有效性和稳定性。

仿真结果表明，当智能车辆以不同车速行驶时，为躲避可能碰撞的障碍物，提出的控制器牺牲了规划局部轨迹与预先设定的全局参考轨迹之间的跟踪精度。由图4 可知，车辆以30、60、90 km/h 速度行驶时，2 种规划控制器都使车辆顺利避开障碍物且在最后都跟踪上了全局参考轨迹，由图5 可得，实际行驶轨迹与全局参考轨迹之间的最大偏差分别为0.50、0.69、0.92 m。结果表明提出的控制器在低、中、高速工况下都可以有效避开障碍物，且实际行驶轨迹与全局参考轨迹之间的横向误差也足够小。

图4 不同行驶速度下的车辆轨迹Fig.4 Moving trajectories of vehicle at various velocities

图5 不同行驶速度下的横向偏差Fig.5 Lateral deviation of vehicle at various velocities

在30、60、90 km/h 车速下，汽车避障行驶的质心侧偏角变化情况如图6 所示。结果显示，车辆以不同车速进行避障跟踪时，质心侧偏角峰值分别为0.53°、0.02°和0.88°，均不超过1°，控制在一个较小的范围内。

“王九，不要着急，慢慢的会有人来的，你瞧，这莲蓬，不是大爷们的路数？咱们呆一会儿，就来玩个什么给爷们看看，玩得好，还愁爷们不赏三枚五枚？玩得好，大爷们回家去还会同家中学生说：嗨，王九赵四摔跤多扎实，六月天大日头下扭着蹩着搂着，还不出汗！（他又轻轻的说）可不是，你就从不出汗，天那么热，你不出汗也不累，好汉子！”

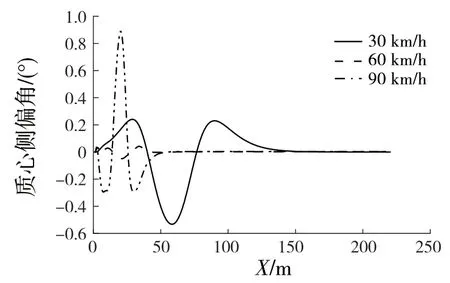
图6 不同行驶速度下的质心侧偏角Fig.6 Side-slip angles of vehicle at various velocities

图7 显示，随着车速的提高，车辆在进行主动避障时，横摆角速度值会相应提高。在汽车附着系数为0.85 的路面上，汽车以30 km/h 速度行驶时，横摆角速度峰值为3.94 (°)/s；以60 km/h和90 km/h 速度行驶时，横摆角速度的峰值分别为6.98 (°)/s 和10.45 (°)/s。上述横摆角速度峰值均在15 (°)/s 的行业经验限制范围内[16]。实验结果表明，改进后的控制器能够保证车辆在避障行驶时的稳定性，避免车辆失稳的发生。

图7 不同行驶速度下的横摆角速度Fig.7 Yaw velocity of vehicle at various velocities

图8 显示，当汽车以30 km/h 和60 km/h 速度行驶时，最大侧向加速度均不超过0.4g 的行业经验限制[16]，但当车辆90 km/h 高速行驶时，侧向加速度在躲避障碍物时会短暂超过0.4g，之后车辆又恢复稳定行驶 。

图8 不同速度下的侧向加速度Fig.8 Lateral acceleration of vehicle at various velocities

4 结语

针对车辆主动避障技术，提出了基于车辆点质量模型和车辆三自由度动力学模型建立的分层控制架构的规划控制器。在上层局部轨迹规划器中提出了改进了的避障惩罚函数，同时在下层轨迹跟踪控制器中融入了车辆安全行驶包络线约束，保证车辆避障行驶的稳定性。

通过MATLAB/Simulink 和CarSim 联合仿真，得出主要结论：（1）提出的双层MPC 规划控制器可以成功避开障碍物，保证实际行驶轨迹与全局参考轨迹之间偏差较小，并且在规避障碍物后可以重新跟踪全局参考轨迹；（2）车辆以低中高速进行避障行驶时，控制器可以确保车辆稳定参数均在允许范围内，说明提出的规划控制器可以有效保证车辆行驶的安全稳定性。