球面手腕康复机构逆运动学解新方法及应用
2023-08-25焦文杰姬帅旭郝惠敏黄家海李利娜李诗雨
焦文杰,姬帅旭,郝惠敏,黄家海,李利娜,李诗雨
(太原理工大学 机械与运载工程学院,山西 太原 030024)
随着国内人口老龄化的加速,中风发病率呈逐年增加的趋势.据统计可知,国内中风患者目前已达1 300多万,预计2030年可能会超过3 000万人[1].中风患者的高效康复训练是当前的关注点之一,相对于传统理疗和药物治疗,康复机器人可以节约大量人力、物力,手腕康复训练装置是其中之一[2-3].
近年来,国内外学者对腕部康复机器人/装置开展了较多的研究工作,如气动人工肌肉手腕康复装置[4]、绳索驱动腕部康复机构[5]、混联式腕关节康复机构[6]以及基于3RRR球面并联机构(spherical parallel mechanism,SPM)的手腕康复装置[7].其中,SPM手腕康复装置具有结构紧凑、贴合手腕运动特征的优点.
SPM具有俯仰、偏航和滚动的运动特点[8],Gosselin等[9-11]对该机构的运动学特性开展了一定的研究工作.通常将该机构逆运动学的研究转换为3个一元二次方程的求解问题,由于方程组最多存在8个解,给驱动系统控制器的设计带来了一定的挑战[12].目前,3RRR球面并联机构逆运动学唯一解的求解方案有2个:方案1是建立3RRR球面并联机构逆运动学方程,选取一元二次方程正根对应的解作为机构逆运动学解[13];方案2是在8组解中选取与初始姿态相同工作模式的一组解作为唯一的逆运动学解[14-15].上述2种方案都存在不足,方案1存在部分动平台姿态无逆运动学解的问题,方案2不能得到具体的逆运动学解析解.
针对共轴3RRR球面并联机构(CSPM)逆运动学唯一解求解方法的不足,提出基于欧拉角的逆运动学分步求解方法.该方法将基于欧拉角描述的动平台姿态分解为绕Z轴和绕X、Y轴旋转的子姿态A和子姿态B,并分别求解出子姿态A的逆解和子姿态B的最优解,将2个子姿态最优解线性相加,可以获得CSPM唯一逆解.将该方法与单位四元数相结合,并应用于球面手腕康复装置的轨迹规划中,以提高装置运动控制的实时性,这对CSPM控制器设计具有实际的工程意义.
1 球面手腕康复机构的运动学模型
1.1 人体腕关节的简介
人体腕部具有3个自由度,以人体腕部建立坐标系,腕部分别可实现绕Z轴转动的屈曲(F)/伸展(E)运动、绕Y轴转动的内收(A)/外展(O)和绕X轴转动的旋内(M)/旋外(L)运动,如图1所示.由GB/T 15499—1995及其他资料[16-17]可知,正常情况下实现所述6个运动时手腕转动角度γ的范围,如表1所示.
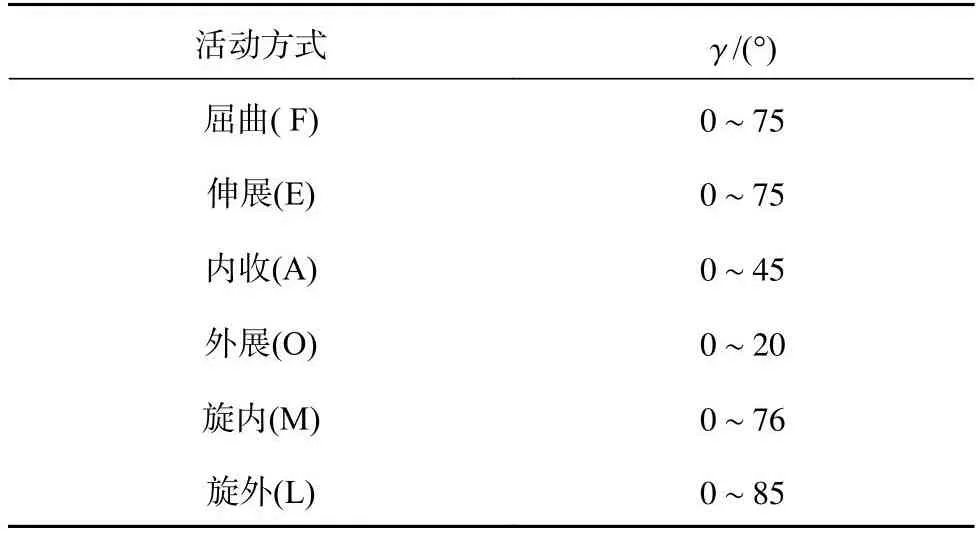
表1 手腕活动范围Tab.1 Wrist range of motion

图1 人体腕关节运动模型Fig.1 Human wrist joint movement model
1.2 坐标系设定
共轴3RRR球面并联机构如图2所示,由3个近端连杆(弯曲弧度为α1)、3个远端连杆(弯曲弧度为α2)、动平台和底座组成,其中近端连杆为驱动杆.近端连杆与底座、近端连杆与远端连杆、远端连杆与动平台均采用转动副连接,使得CSPM动平台在空间中只能作旋转运动,与手腕运动相贴合.在初始条件下,CSPM动平台和底座呈水平状态,3根近端连杆呈120°均匀分布.CSPM的特点是所有关节轴线相交于O点,后文将其称为旋转中心.
以图2的O点为坐标原点建立固定坐标系,Z轴垂直于底座,方向向上.在共轴3RRR球面并联机构中,3根驱动轴存在共轴关系,驱动杆轴向量、近端连杆与远端连杆相连的轴向量、动平台姿态向量分别采用Ui、Wi、Vi(i= 1,2,3)表示.Vi与Z轴的夹角为β.定义Z轴与Wi所组成的平面为测量平面Pi(i= 1,2,3),Y轴位于P1平面内,利用右手定理可以确定X轴方向.
设定驱动轴关节转角θ=[θ1,θ2,θ3]是测量平面Pi转动的角度,逆时针方向为正,顺时针为负,如图3所示.在工作空间内,使用XYZ欧拉角表示动平台姿态,初始姿态下,动平台呈水平状态,设定驱动杆转角为θ=[θ1,θ2,θ3].
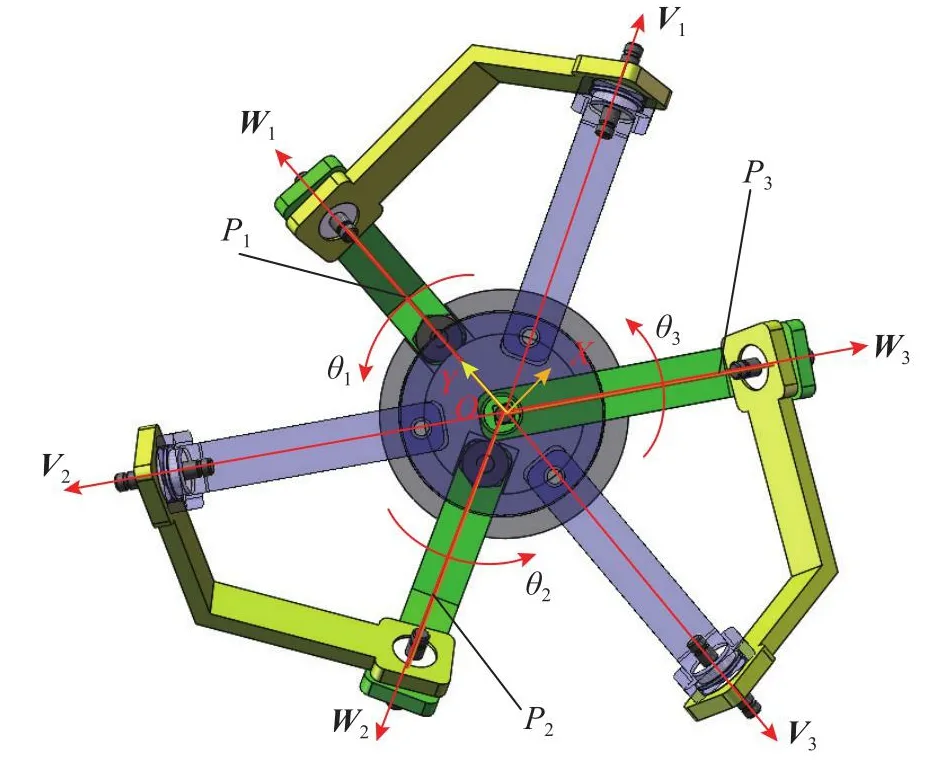
图3 CSPM驱动轴正方向的设定Fig.3 Setting of CSPM drive shaft positive direction
1.3 运动学模型
1) 初始姿态.在固定坐标系下,3个驱动轴单位向量相同,
在初始时刻,Wi*(i=1,2,3)为
式中:α1为机构参数;ηi=2(i-1)π/3,i=1,2,3.
在初始姿态下,V1水平投影与平面P1的夹角为δ,如图3所示.根据几何关系可知,在初始时刻,
式中:β为机构参数.
2) 非初始姿态.当输入角度为θi时,Wi为
动平台姿态Vi为
式中:
其中,φ1、φ2、φ3为欧拉角参数.
2 基于欧拉角逆运动学求解的新方法
使用欧拉角()表示动平台姿态,CSPM最多存在8组逆运动学解,但只有一组解满足与初始姿态工作模式相同的要求,称为手腕康复装置的唯一逆运动学解.
2.1 共轴球面并联机构求解的新方法
联立式(4)、(5),根据几何约束列出方程:
将式(4)、(5)代入式(7),可以简化为
由于CSPM具有3根输入轴重合的特征,当动平台绕Z轴旋转φ时,3个驱动杆也会旋转φ.由此可知,在CSPM逆运动学的求解过程中,驱动杆旋向差异主要取决于动平台姿态角φ1、φ2.基于上述特性,提出基于分步计算CSPM逆运动学求解的新方法.将动平台姿态分解为绕Z轴和绕X、Y轴旋转的2个部分,分别计算出2个部分姿态近端连杆所需的最优输入角度及;根据输入轴重合的特点,将进行加法运算后,得到完整的逆运动学解.
1)根据CSPM的特点,将动平台姿态分解为绕X、Y轴旋转的和绕Z轴旋转的,动平台姿态向量使用Vi表示.
3)根据式(10)计算:
4)结合式(9),可得
5)利用式(9)、(10),计算Ti对应的关节转角.
式中:min表示取最小值,abs表示取绝对值.
7)当动平台绕Z轴旋转0,0,φ3时,近端连杆所需的输入角度为
将θ*与进行加法运算后,可得唯一的逆运动学解,即当CSPM动平台旋转角度φ1,φ2,φ3时,近端连杆输入角度为
对上述过程归纳整理后,得到如图4所示的唯一逆运动学解流程图.
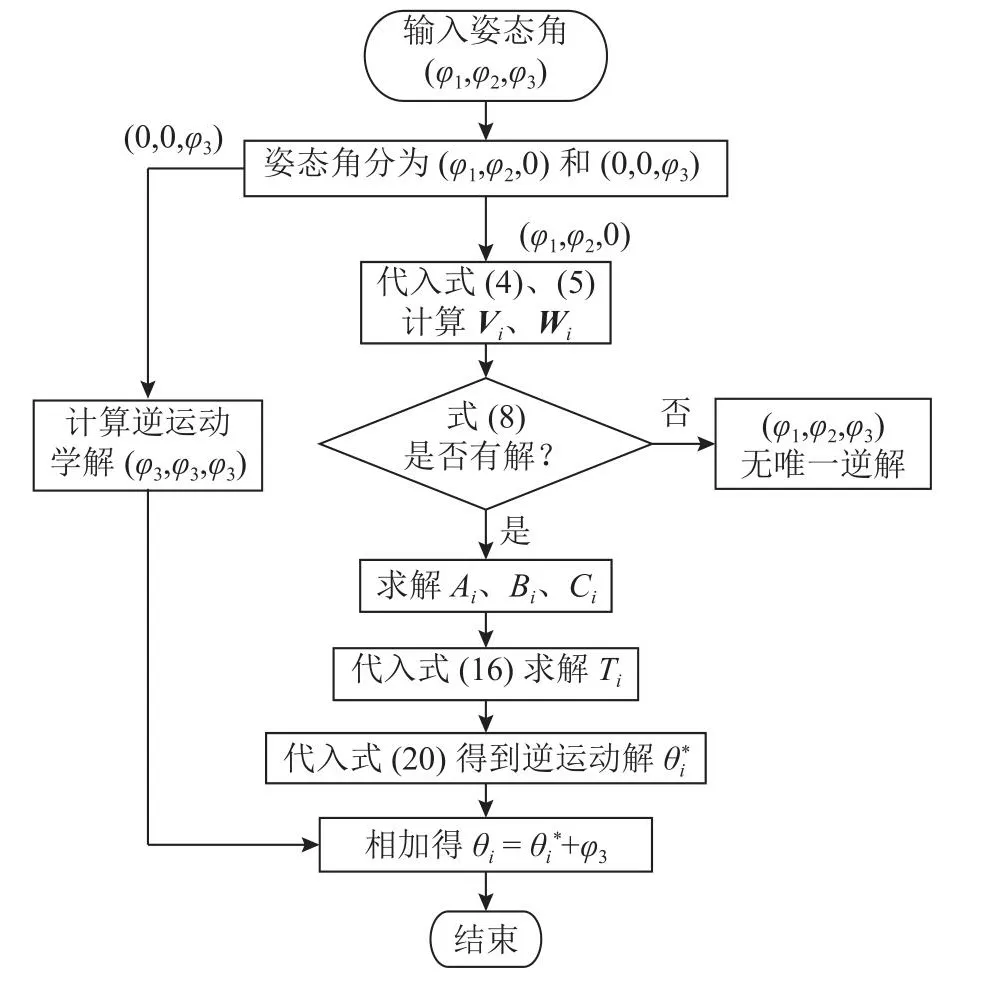
图4 求解唯一逆运动学解的流程图Fig.4 Flow chart for solving unique inverse kinematics
2.2 结果验证与讨论
以图2所示的共轴3RRR球面并联机构为例,机构参数为α1=50°,α2=57.6°,β=75°,δ=60°.机构的装配方式为远端连杆均在近端连杆的左侧,如图3所示.设动平台的位姿角为(30°, 15°, 20°),利用式(5)求解得到
根据式(14)~(19),求解得到
利用文献[14]的正运动学方法对逆运动学新解法进行验证,将得到的逆运动学解θ代入式(4),可得
根据CSPM动平台任意2个姿态向量之间的几何约束关系,存在
式中:φ3为相邻姿态向量Vi之间的夹角,有α3=2arcsin(cosβcos(π/6)).
将式(5)、(27)代入式(7),结合式(27)、(28)可得
式中 :v1x、v1y、v1z为V1的X、Y、Z轴分量.
根据机构初始姿态下的装配方式,确定方程的初值为
使用matlab中的fsolve函数,求解得到
将式(31)的正运动学解与式(25)所示的初始值进行对比可知,两者的误差非常小,验证了所提方法的正确性.
3 基于逆解新方法的手腕康复机构工作空间
3.1 奇异位形分析
手腕康复装置的奇异性是指CSPM处于某些特殊姿态时会失去固有刚度且机构可控性变差.球面并联机构运动路径应该远离奇异位形,以免机构丧失自由度,降低机构的可控性.
对式(7)求导,得到
将式(33)、(34)代入式(32),化简得到
式中:J为雅可比矩阵,J=[J1,J2,J3]T,
条件系数定义为
通过ζ(J)可以判断机构姿态是否处于奇异位形.当ζ(J)→0时,CSPM姿态处于奇异位形附近;反之,CSPM姿态远离奇异位形.定义ζmin(J)来判定机构位姿点是否位于工作空间内,参考众多研究, 将ζmin(J)定义为0.25.
3.2 连杆碰撞检测
根据文献[18]可知,CSPM连杆碰撞的原因是相邻驱动杆之间的夹角过大或者过小,本文采用欧式距离判断碰撞是否发生.如图5所示,假设近端连杆和远端连杆的连接点为Bi(i=1,2,3),动平台与上端连杆的连接点为Ci(i=1,2,3).通过几何距离测量可知,共轴上点Ai、Bi、Ci与O点的欧式距离都为100 mm,即OAi=OBi=OCi=100mm,计算Ai、Bi、Ci在固定坐标系下的坐标为
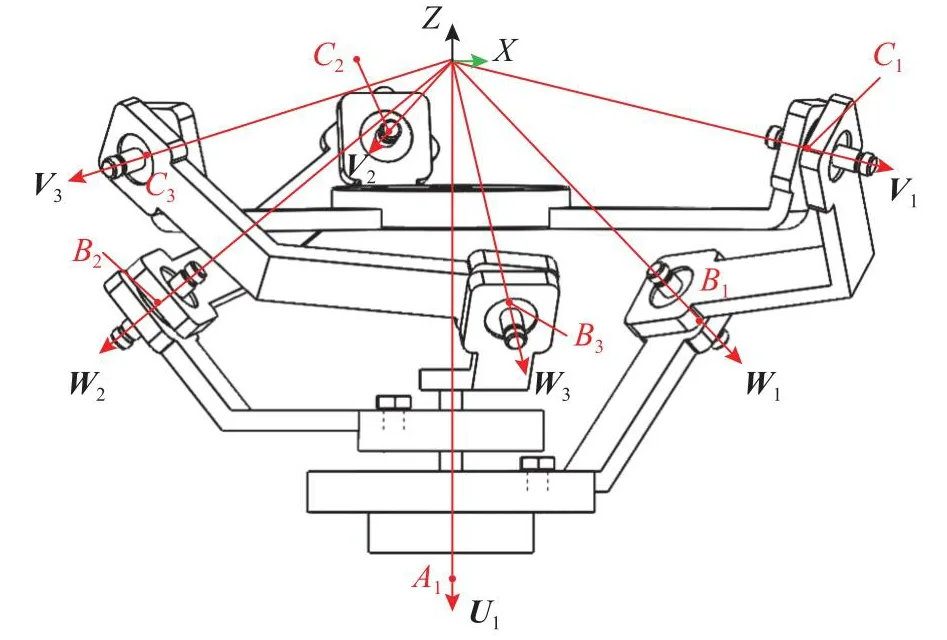
图5 3RRR球面并联机构连接点位置Fig.5 3RRR spherical parallel mechanism connection point position
CSPM在运动过程中只能发生以下2种类型的碰撞[18]:1)在相邻2个驱动杆与远端连杆的连接点处发生碰撞;2)动平台与底座之间发生碰撞.
对于所研究的CSPM手腕康复装置而言,第1类碰撞是近端连杆末端之间发生碰撞.设定碰撞点为D,如图6(a)所示,此时测量BiBj=22mm,i、j=1,2,3,i≠j,因此碰撞边界条件为
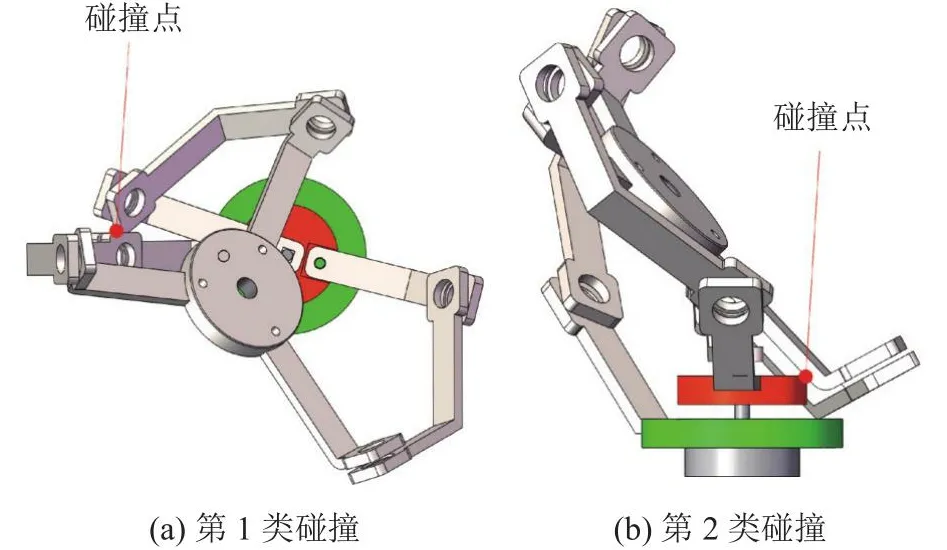
图6 不同碰撞的碰撞点位置Fig.6 Collision point position of different collisions
对于所研究的CSPM手腕康复装置而言,第2类碰撞是动平台与底座边缘之间发生了碰撞,碰撞点为F,如图6(b)所示.此时测量∠AiOCi=22°,ACi=38mm(i=1,2,3),碰撞的边界条件为
3.3 手腕康复机构的姿态角空间与实际工作空间
对于CSPM 手腕康复装置而言,设定不发生奇异和碰撞的欧拉角=为姿态角工作空间Ω.采用蒙特卡洛法进行工作空间计算,采样点数为200 000,假设绕X轴转动的姿态角φ1的采样范围为[-90°,90°];绕Y轴转动的姿态角φ2的采样范围为[-90°,90°];绕Z轴转动的姿态角φ3的范围为[-180°,180°].以每一个采样点姿态角对应的ζ(J)是否大于0.25以及是否满足第1、2碰撞条件作为判断依据,若某一采样点姿态角满足上述条件,则判定该点属于欧拉角工作空间Ω.由于CSPM在工作空间可以绕旋转轴无限旋转,求解得到工作空间中绕Z轴转动角度φ3仍为[-180°,180°],如图7所示.
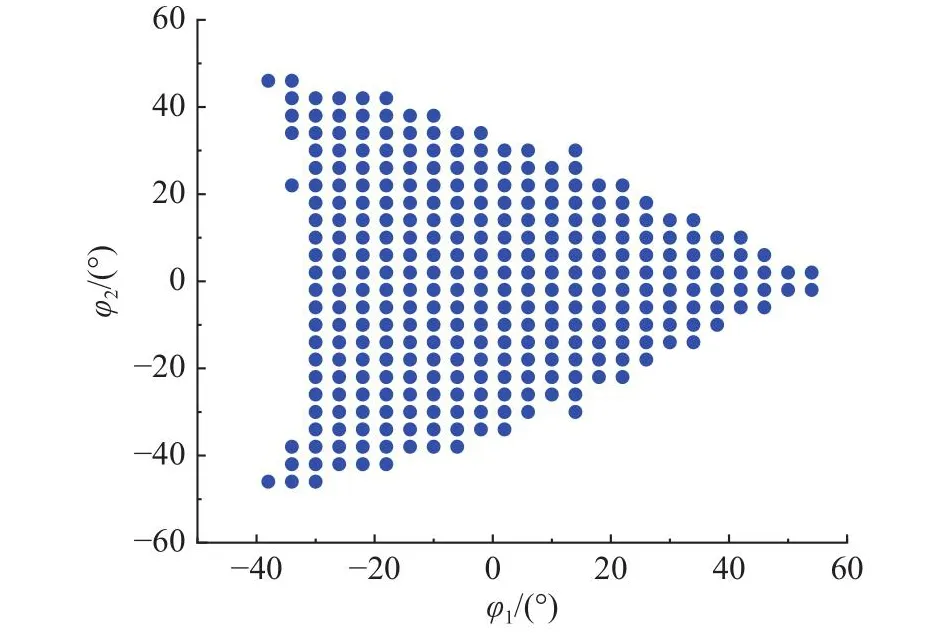
图7 CSPM欧拉角工作空间Fig.7 Euler angle workspace of CSPM
为了确保中风患者康复训练时的手腕运动角度小于表1所示的极限运动角度,避免患者手腕受到损伤,将CSPM手腕康复装置的实际运动空间限定在以下范围:φ3转动角度为,φ2转动角度为-15°,30°,φ1转动角度为.如图8所示.
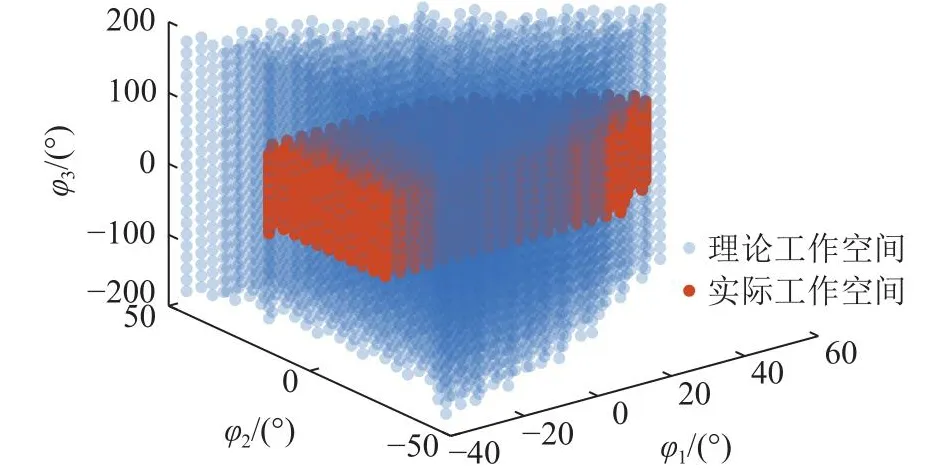
图8 CSPM实际工作空间Fig.8 Actual workspace of CSPM
4 逆解新方法在路径规划中的应用
根据CSPM手腕康复装置的设计目标,使用者只能在固定轨迹下进行康复训练.根据欧拉角和单位四元数之间存在的转换关系,可以将手腕实际工作的空间姿态点转化为单位四元数,结合所提的逆运动学新方法与单位四元数插补,实时得到平滑的曲线.
4.1 单位四元数插补
q可以表示为
单位四元数q可以转化为欧拉角:
设定机构起始姿态为初始位姿,经过旋转变换q1,机构姿态为“姿态1”;在初始位形下经过旋转变换q2,q1≠q2机构姿态为 “姿态2”,如图9所示.
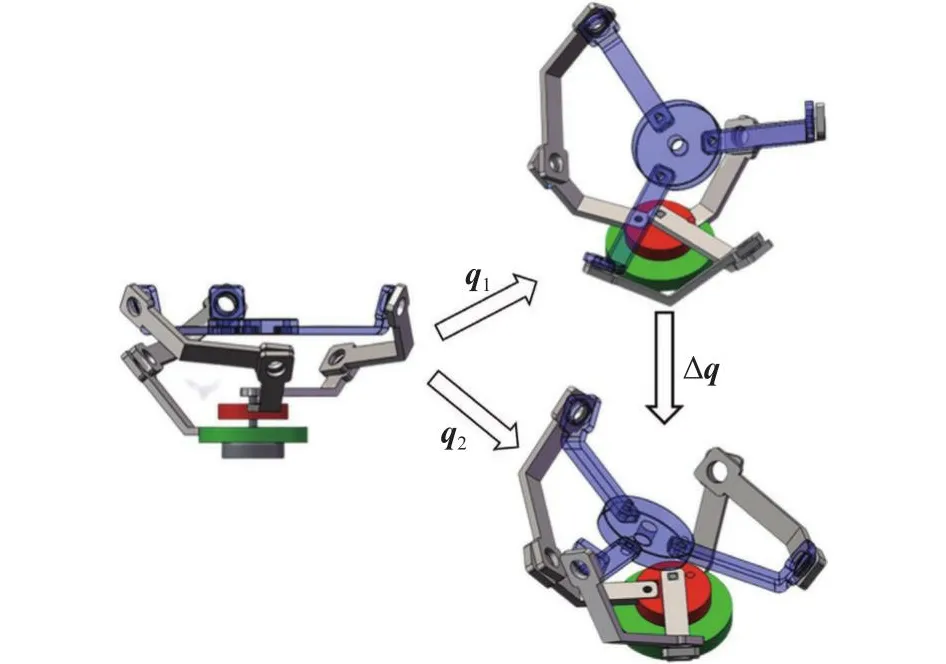
图9 单位四元数表示旋转Fig.9 Unit quaternion representation rotation
从图9可知,“姿态1”与“姿态2”可以通过单位四元数Δq表示:
根据单位四元数性质q-1=q*,得到“姿态1”到“姿态2”的插补表达式:
式中:q*1为q1的共轭四元数,t为时间.
将插值点qt使用式(47)转化为欧拉角,利用求解运动学唯一逆运动学解的方法对全部插值点进行求解,可以得到路径点的关节转角.
4.2 实验验证
搭建如图10所示的实验装置.选择初始位姿γ1=[0°,0°,0°]为“姿态1”,在CSPM手腕康复机构实际工作空间中选取为“姿态2”,代入式(45)转换为单位四元数:

图10 手腕康复机构样机Fig.10 Wrist rehabilitation mechanism prototype
通过LabVIEW编写上位机程序,arduino编写下位机程序,下位机接收上位机发送的初始点和终点欧拉角度,使用所提的方法进行运动学逆求解及驱动步进电机.通过查询相关资料,将实验运动时间设定为4 s,采用等值压缩方法,将运动时间点映射到[0,1.0],并代入式(47)获得路径点姿态.为了保证实验过程中速度更加平滑,引入T型曲线规划算法规划速度.使用无线位姿传感器测量动平台姿态,反馈给上位机.
实验结果和理论结果如图11所示.可知,理论计算结果与试验测试结果均为光滑曲线,φ1、φ2的最大误差约为1°,φ3的最大误差约为2.5°,误差均在合理范围内.上述结果表明,所提的逆运动解方案是可行、可信的.该实验过程中的误差产生原因如下.1)实验为开环控制策略.2)结构安装误差.转动副在安装过程中未能消除间隙,导致了动平台姿态误差的产生.3)零件弹性变形.驱动杆和远端连杆发生了微小的弹性变形,造成了动平台的姿态误差.图11所示的实验曲线比较光滑,表明CSPM手腕康复机构在运动过程中姿态变化平滑,为后续手腕康复机构的实时控制器设计提供了良好基础.

图11 轨迹规划中欧拉角实验值与理论值的对比Fig.11 Comparison of experimental value and theoretical value of Euler angle in trajectory planning
5 结 论
(1) 提出并验证了共轴3RRR并联机构逆运动学解的新方法,解决了球面手腕康复装置逆运动学解完备性和无解析解的问题.
(2)基于逆运动学解的新方法,以无连杆碰撞和无奇位形为约束条件,得到手腕康复装置欧拉角姿态空间.通过分析手腕运动的特点,获得手腕康复装置实际工作空间:
(3) 提出并验证了基于四元数插补的实时轨迹规划方案,φ1、φ2的最大误差为1°,φ3的最大误差为2.5°,为手腕康复机构的控制器设计提供了基础.
