多参数耦合作用下海洋立管动力响应实验
2023-08-23郑润王春光何文涛张震洋任梦琪
郑润, 王春光,2*, 何文涛, 张震洋, 任梦琪
(1.山东理工大学建筑工程与空间信息学院, 淄博 255000; 2. 山东省海洋工程重点实验室, 青岛 266100; 3.中国海洋大学工程学院, 青岛 266100)
全球正面临着日趋严重的能源危机,中国能源过度依赖海外是一个亟需解决的问题。相对于陆地油气资源,全球海洋油气资源更加丰富,据统计,未被开发的海上油气储量的90%是在超过1 000 m水深的海底地层下,而中国深海面积广阔,海上油气资源非常丰富[1],海洋油气开发是解决能源危机的重要方法[2]。
海洋立管在整个海洋油气开发中扮演着举足轻重的角色,它是将海底油气输送到海洋平台的管道。海洋环境复杂多变,在洋流作用下,海洋立管两侧会交替产生从立管表面分离出来的涡旋,即产生卡门涡街现象,进而引起立管的涡激振动(vortex induced vibration, VIV)。Ferguson 等[3]开创性的采用声学液位压力传感器的实验研究,发现了圆柱体涡旋激发震荡的表面和尾流现象。涡激振动将导致立管的疲劳破坏,为了防止立管的疲劳破坏,Liu等[4]提出建立立管涡激振动的预测模型是抑制涡激振动的重要手段,并提出大长径比立管的涡激振动研究还需进一步深入。马烨璇等[5]提出要结合不同环境,不同条件,从而给出相对应的抑制涡激振动的方法,这就要求学者们综合考虑多因素的共同影响。但目前多数研究仍停留在单因素或少量几个因素的影响研究上,多因素耦合作用涉及不多。
影响海洋立管动力响应的主要因素包括:立管本身的材料特性、洋流流速、顶部张力、边界条件以及波浪等。以往的研究往往只针对单因素影响作用进行探索。关于顶张力对立管在涡激振动中频率的影响方面,Yang等[6]通过实验得出预张力的增加,组合激励下的顶部张紧提升管(top-tensioned riser,TTR)的不稳定性会被抑制,但抑制效果的提升与预张力增加不成比例。李文华等[7]将立管简化为典型的 Euler-Bernoulli 弹性梁模型,根据传递矩阵理论得出表观重力和立管内外侧压力差引起的海洋立管轴向拉力的变化可影响立管本身固有频率的结论。张永波等[8]针对顶张力因素对立管涡激振动的影响进行研究,并根据实验数据得出立管的自振频率会随着顶张力的增大而增大的结论。关于来流方向,柳军等[9]通过实验得出结论,在均匀流速条件下,立管的顺流向涡激振动频率基本是横流向涡激振动频率的2倍,顺流向涡激振动也应受到重视,特别是在高速流下,需同时重视两个方向的影响。殷布泽等[10]通过总结过往的海洋立管涡激振动实验提出要更加注重波浪对于海洋立管涡激振动的影响。李莹等[11]针对边界条件对幅值影响进行研究,发现同种情况下,两端铰接时立管的振动幅度大于立管两端固接时的振动幅度,Gao等[12]通过数值分析方式研究得出在一定范围内立管长径比(L/D)越小,不同边界条件下的涡激振动位移差异越大。此外,巫志文等[13]建立了随机波浪和涡流激励联合作用下海洋立管动力响应的数学分析模型,并利用该模型探索了随机波浪对立管涡激振动的影响情况。Wang等[14]进行了多因素实验,研究了立管材料、流速、顶张力和边界条件几个因素综合对立杆涡激振动的影响,但是并没有考虑波浪的影响。葛士权等[15]通过利用ANSY软件进行海洋立管多因素耦合作用下涡激振动的有限元分析。
现借鉴崔阳阳等[16]和娄敏等[17]的立管实验设计方案,并进行优化和改进,即在立管的一个观测点上粘贴8个应变片,不仅在顺流向和立管横向进行应力应变的检测,同时对单个点位的XY两个方向进行观测。因此在前人基础上,现考虑立管本身材料,洋流流速、顶部张力、边界条件以及波浪等多方面的因素,开展洋流-波浪-立管耦合作用下的海洋立管动力响应的模型实验及各参数影响性分析。
1 海洋立管动力响应设备
为了研究海洋立管动力响应特性,设计了电测法实验方案。实验主体为铝管(aluminium,Al)和有机玻璃管(polymethyl methacrylate,PMMA)。试验系统由波流系统、流场监测系统、边界条件施加系统、数据采集系统构成。
1.1 实验主体
海洋立管模型是本次研究的实验主体,目前常见的钢制立管多采用弹性模量为207 GPa的X80高强度钢,而新型纤维增强复合材料海洋立管的等效弹性模量约为30 GPa,两类海洋立管的弹性模量相差大[18]。为了定性分析两类不同材料海洋立管弹性模量的影响,本次实验分别采用了弹性模量相差大的铝管和有机玻璃管模型定性代表工程实际中的钢制海洋立管和纤维增强复合材料海洋立管[14]。海洋立管模型尺寸为外径20 mm,壁厚2 mm,长度1 250 mm。具体海洋立管模型尺寸及属性如表1所示。

表1 立管模型尺寸及材料弹性模量Table 1 The size and the elastic modulus of the materials
作为弹性阶段的表征,铝管及有机玻璃管的拉伸弹性模量与压缩弹性模量结果相差不大,采用材料压缩弹性模量(图1)实验确定其参数,结果如表1所示。利用应变片获得材料应变数据。根据水槽参数与实验目的,确定水深采用0.7 m,即Z=0.7 m位置是水平面。在Z=0.30、0.60、0.90 m处,环立管一周等距布置4组应变片,每组应变片分为立管径向(y)和立管环向(x)两个。

图1 压力实验机Fig.1 The pressure tester
在顺流方向,以水流第一个经过的位置,即迎水面位置设为A,水流后经过的位置,即背水面位置设为C。在横流向方向,分别为B和D。具体布置如图2所示。

图2 应变测点粘贴位置图Fig.2 Location of pasted strain gauge
1.2 波流系统
实验场地位于中国海洋大学的山东省海洋工程重点实验室,波流系统在实验室中的清水水槽来实现,该波流联合水槽内径1 m、高1.2 m、长30 m,能够制造出不同流速的均匀流与不同波浪要素的波,如图3所示。

图3 波流联合水槽Fig.3 Combined current and wave channel
采用的波流系统可控流速范围为0~1.2 m/s,可控波浪周期为0.8~2 s,可控波高为1.5~15 cm。
根据文献[19]可知,墨西哥湾的百年洋流和百年飓风条件下的洋流流速相差约1.8倍,波高相差4.5倍,波浪周期相差1.8倍,同时考虑试验设备性能,本次试验流速选择相差2.3倍的0.3 m/s和0.7 m/s,波高选择相差3倍的5 cm和15 cm,波浪周期选择相差2倍的1 s和2 s,用以定性模拟不同工况下的海洋环境情况。
1.3 波流监控系统
水槽控制系统中设定的流速为造流口流速及造波口波浪参数,经过立管流速及波浪参数有差异,故需结合流速及波高监控系统调整造流流速及波浪参数,使得流经立管的流速及波高参数达到实验要求。流经立管模型的流速及波高的测量采用天津水运工程科学研究院的多路流速仪及波高仪测定。为了尽量减少流速仪及波高仪对立管模型的干涉影响和切实保证过立管的流速与波浪参数符合要求,将流速仪及波高仪放置在立管模型前约2 m。具体仪器外形和信号采集设备如图4所示。

图4 流速及波浪参数监控系统Fig.4 Velocity and wave parameter monitoring system
1.4 边界条件施加系统
1.4.1 铰支顶座
本次实验的上端边界为可施加顶张力的铰支座,为此专门设计使用了能使立管小幅度转动的含铰支座的支架。此支架使用时固定在水槽上方不动,使管件上部穿过铰支座,夹到推拉力计的夹具上,给立管模型提供上端铰接的边界条件。使用前需加润滑油降低摩擦力,避免立管与上支座摩擦,消耗立管振动的机械能,影响实验结果。具体上端铰接支架图如图5所示。

图5 实验上端支架Fig.5 Top simple support in the experiment
1.4.2 HF数显式推拉力计
采用HF数显式推拉力计施加顶张力。HF数显式推拉力计优势在于采用进口传感器,高精度采样芯片,使得测量头中心点更稳定,测量数据更准确。根据立管模型外部特征,采用三爪夹具连接推拉力计和立管模型,如图6所示。根据美国航运局(American Bureau of Shipping,ABS)规范[20]要求,承载力极限状态顶张力验算建议取2.25倍的含泥有效重度,根据本实验模型尺寸及材料情况,其最大含泥有效重度的计算值约为13.2 N。故本实验中选择30 N及10 N,分别定性模拟承载力及正常使用极限状态。

图6 HF数显式推拉力计及连接整体Fig.6 HF digital push &pull tester and integral connection
1.4.3 固支底座与铰支底座
为了研究不同边界条件对立管动力振动的影响,设计了固支底座(图7)与铰支底座(图8)两种底座,以提供不同的边界条件。支座底端固定在半径500 mm、厚度10 mm的圆形涂漆铁饼上,以防底端支座因为水流问题移动位置。

图7 固支底座Fig.7 Fixed support on the bottom

图8 铰支底座Fig.8 Simple support on the bottom
1.5 数据采集系统
使用DH3820N分布式应力应变测试分析系统如图9所示,该系统与电脑连接整体如图10所示。应变片采用BX120-3AA型电阻式应变片。由于此次实验含有水下工况,所以应变片的防水措施必不可少。防水措施选用704RTV硅橡胶。704RTV硅橡胶在常温下接触潮气固化,24 h之后即可投入使用。

图9 动静态应变仪Fig.9 Dynamic static strain gauge

图10 数据采集系统Fig.10 Data collection system
2 实验方法
从5种实验参数(弹性模量、边界条件、顶张力、外流流速、波浪参数)着手,研究了海洋立管动力响应。弹性模量主要靠两种材料的不同来改变,选定Al、PMMA两种材料。边界条件主要选取铰接-铰接(S-S)和铰接-固接(S-F)两种支撑。顶张力选择10 N和30 N。外流流速选取0.3、0.7 m/s两种。波浪考虑周期和波高两个参数,分别选择1 s和5 cm、2 s和15 cm定性代表小波和大波工况。综合以上实验参数,整理32组实验工况,具体工况参数组合如表2所示。
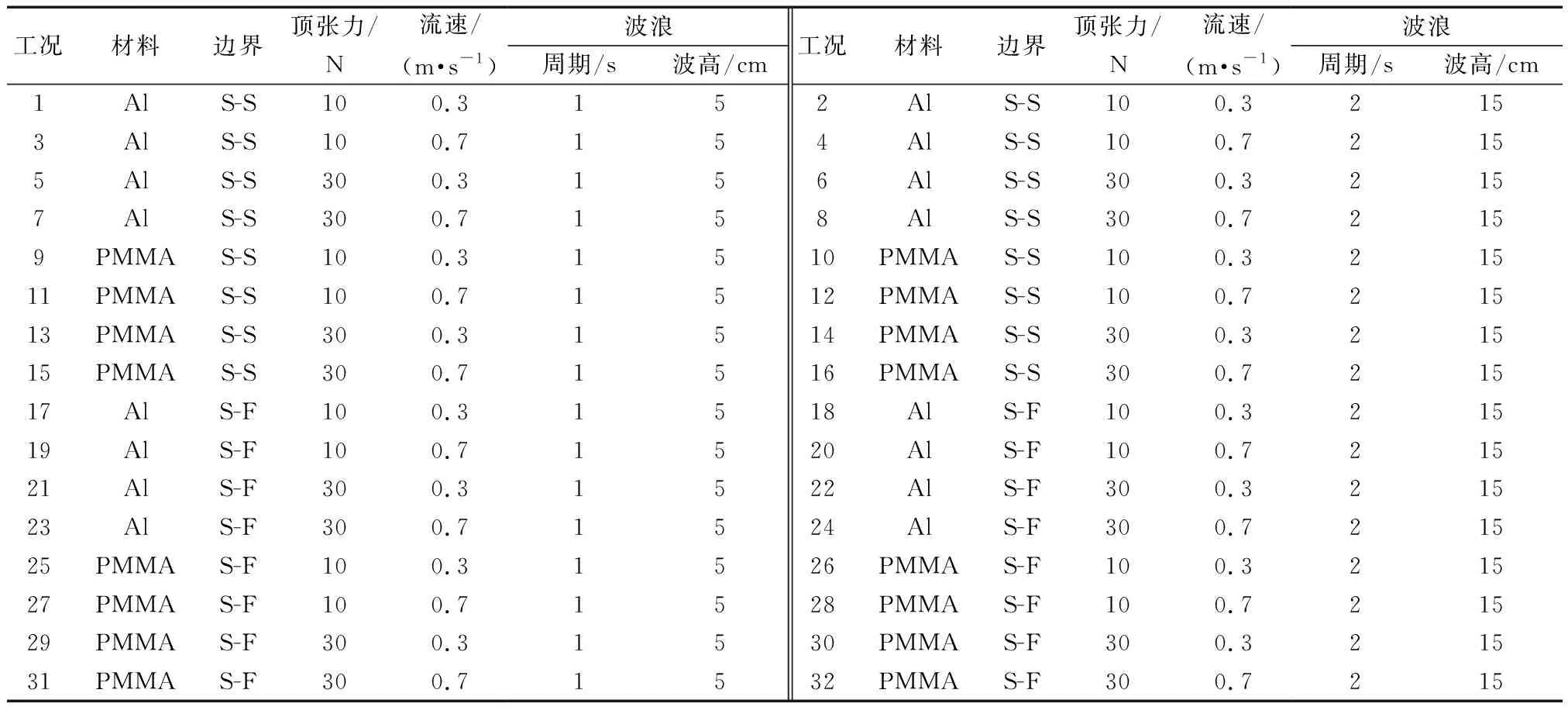
表2 立管实验工况参数组合Table 2 Parameter combination of riser test conditions
对于处于水面以下的应变片采用公共温度补偿片。通过电测法获得到32组实验立管的时域振幅数据,并通过这些数据研究不同实验参数对立管动力响应的影响情况。
3 自振频率
通过等力、等时间间隔敲击,分别采集两种立管模型在水中的时域应变信号,通过傅里叶变换得到各立管模型的自振频率。图11为立管静水中自振波形图和自振频率图以PMMA-(S-F)-10N为例,具体数据如表3所示。

图11 自振波形图Fig.11 Strain history curve of the natural frequency
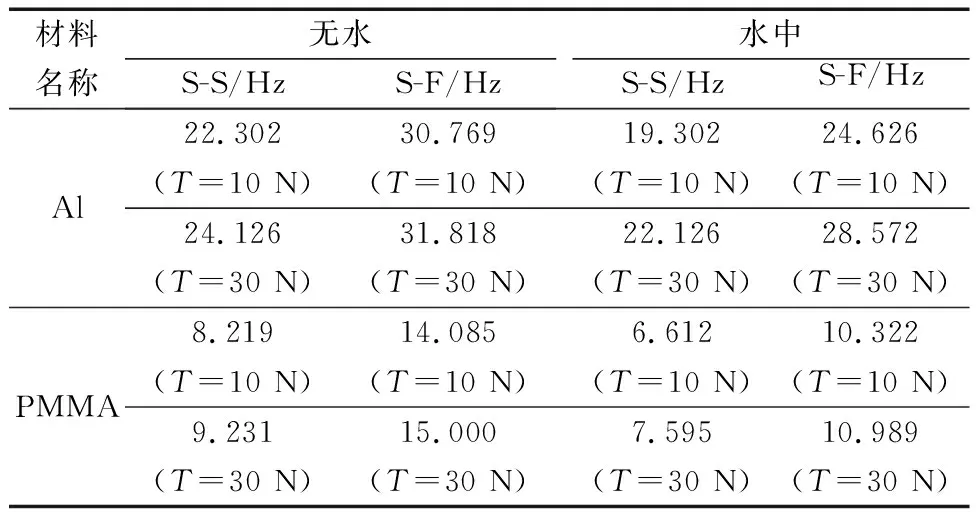
表3 两种边界条件立管自振频率表Table 3 The natural frequency with different boundary condition
从表3可以看出,同条件下,Al管的自振频率高于PMMA管的自振频率。相同边界条件下,立管模型的自振频率会随着顶张力变大而变大。两种材料在等大顶张力作用下,S-S边界条件的立管的自振频率低于S-F边界条件的立管的自振频率,由此得出立管材料的弹性模量、边界条件的约束个数以及施加在立管模型上的顶张力均与立管的自振频率成正相关。
4 立管模型的动力振动响应
4.1 弹性模量对立管顺流向及横流向振动幅值的影响
以工况4和工况12(材料不同,其他参数相同,且为小顶张力、大波浪周期、大流速、大波高、少约束数工况)的Ay(顺流向,z=0.9 m)及By(横流向,z=0.9 m)测点数据为例(图12和图13),说明不同弹性模量对立管顺流向及横流向振动的影响情况。从图12和图13中可以看出,工况4和工况12的顺流向振动幅值分别为36、407 με,横流向振动幅值分别为27、553 με。在两个方向的振动上,在其他条件相同的情况下,Al管的振动幅值小于PMMA管的振动幅值接近,说明两个方向振动幅值均与立管的弹性模量成反比;此外,在立管顺流向振动时发现出现规律性波动现象,波动周期与波浪周期接近。

图13 两种工况下不同立管By点横流向振动应变时程曲线Fig.13 The microstrain time curve for the two different test case in the cross-flow direction of By point
4.2 约束情况对立管顺流向及横流向振动幅值的影响
以工况12和工况28(铰-铰及铰-固约束,其他参数相同,且为小顶张力、大波浪周期、大流速、大波高、小弹性模量工况)的Ay(顺流向,z=0.9 m)及By(横流向,z=0.9 m)测点数据为例(图14和图15),说明不同约束情况对立管顺流向及横流向振动的影响情况。
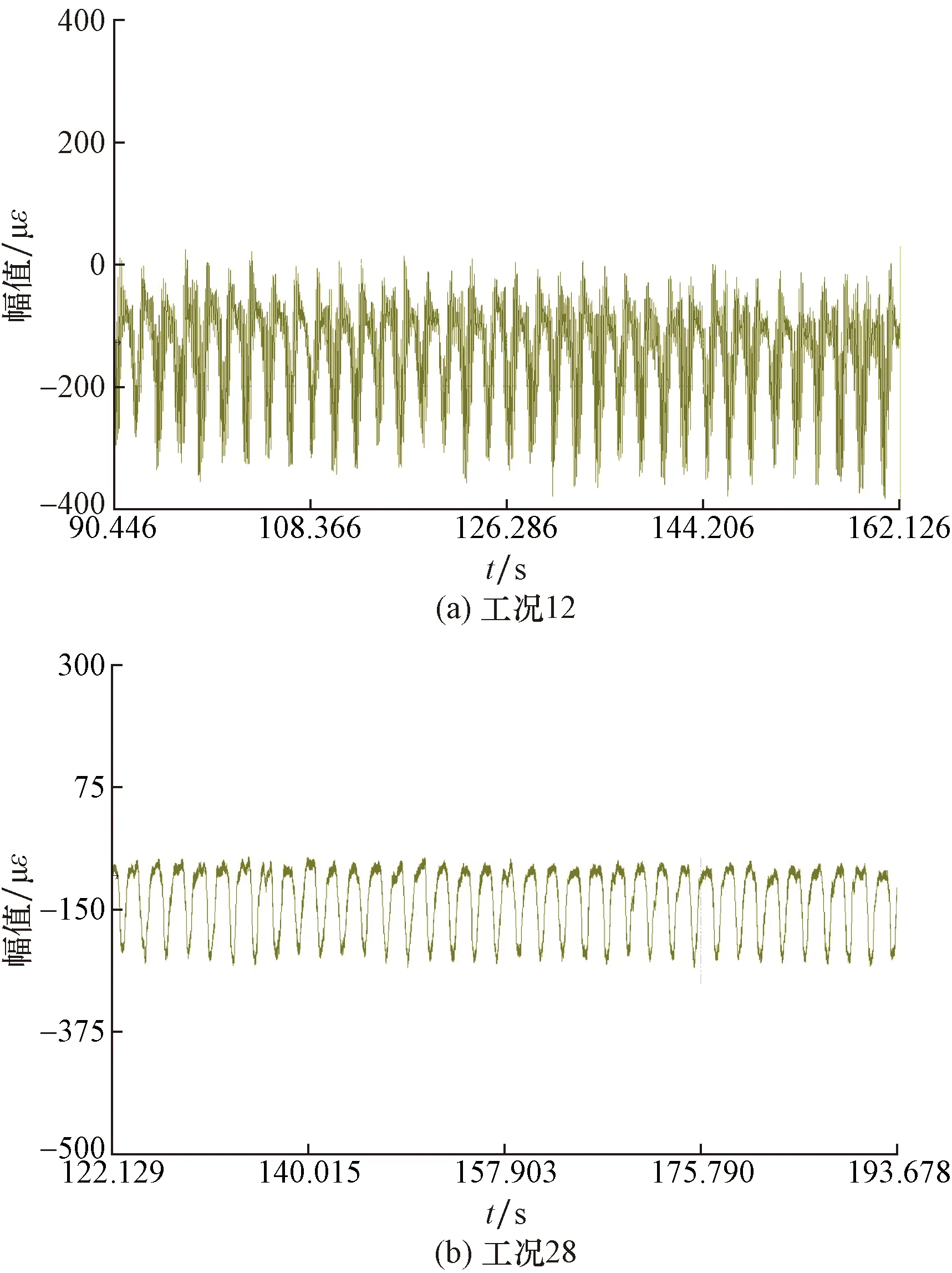
图14 两种工况下PMMA立管Ay点顺流向振动应变时程曲线Fig.14 The microstrain time curve for the two different test case in the flow direction of Ay point
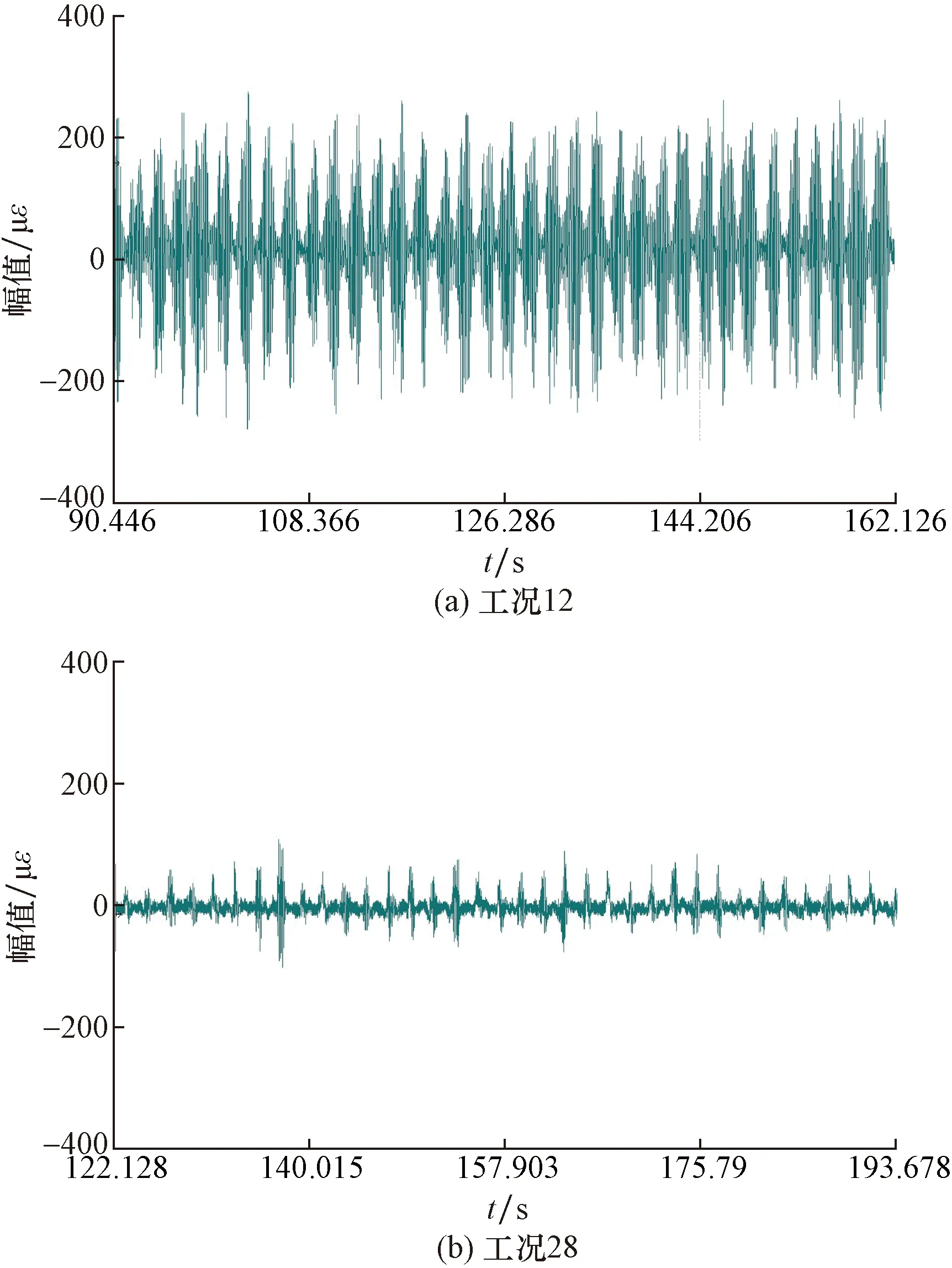
图15 两种工况下PMMA立管By点横流向振动应变时程曲线Fig.15 The microstrain time curve for the two different test case in the cross-flow direction of By point
从图14和图15中可以看出,工况12和工况28的顺流向振动幅值分别为407、205 με,横流向振动幅值分别为553、209 με。在两个方向的振动上,在其他条件相同的情况下,S-F约束在两个方向均明显限制了立管的振动,特别是在垂直来流方向,直接影响到同流速下是否发生明显的涡激振动现象。
4.3 顶张力对立管不同流向振动幅值的影响
以工况12和工况16(顶张力不同,其他参数相同,且为大波浪周期、大流速、大波高、少约束数、小弹性模量工况)的Ay(顺流向,z=0.9 m)及By(横流向,z=0.9 m)测点数据为例(图16和图17),说明不同顶张力对立管顺流向及横流向振动的影响情况。

图16 两种工况下PMMA立管Ay点顺流向振动应变时程曲线Fig.16 The microstrain time curve for the two different test case in the flow direction of Ay point

图17 两种工况下PMMA立管By点横流向振动应变时程曲线Fig.17 The microstrain time curve for the two different test case in the cross-flow direction of By point
从图16和图17中可以看出,工况12、工况16的顺流向振动幅值分别为407、126 με,横流向振动幅值分别为553、141 με。在两个方向的振动上,在其他条件相同的情况下,顶张力的提升在两个方向均明显限制了立管的振动,特别是在垂直来流方向,直接影响到同流速下是否发生明显的涡激振动现象。
4.4 流速对立管顺流向及横流向振动幅值的影响
以工况9和工况11(流速不同,其他参数相同,且为小波浪周期、小顶张力、小波高、少约束数、小弹性模量工况)的Ay(顺流向,z=0.9 m)及By(横流向,z=0.9 m)测点数据为例(图18和图19),说明不同弹性模量对立管顺流向及横流向振动的影响情况。
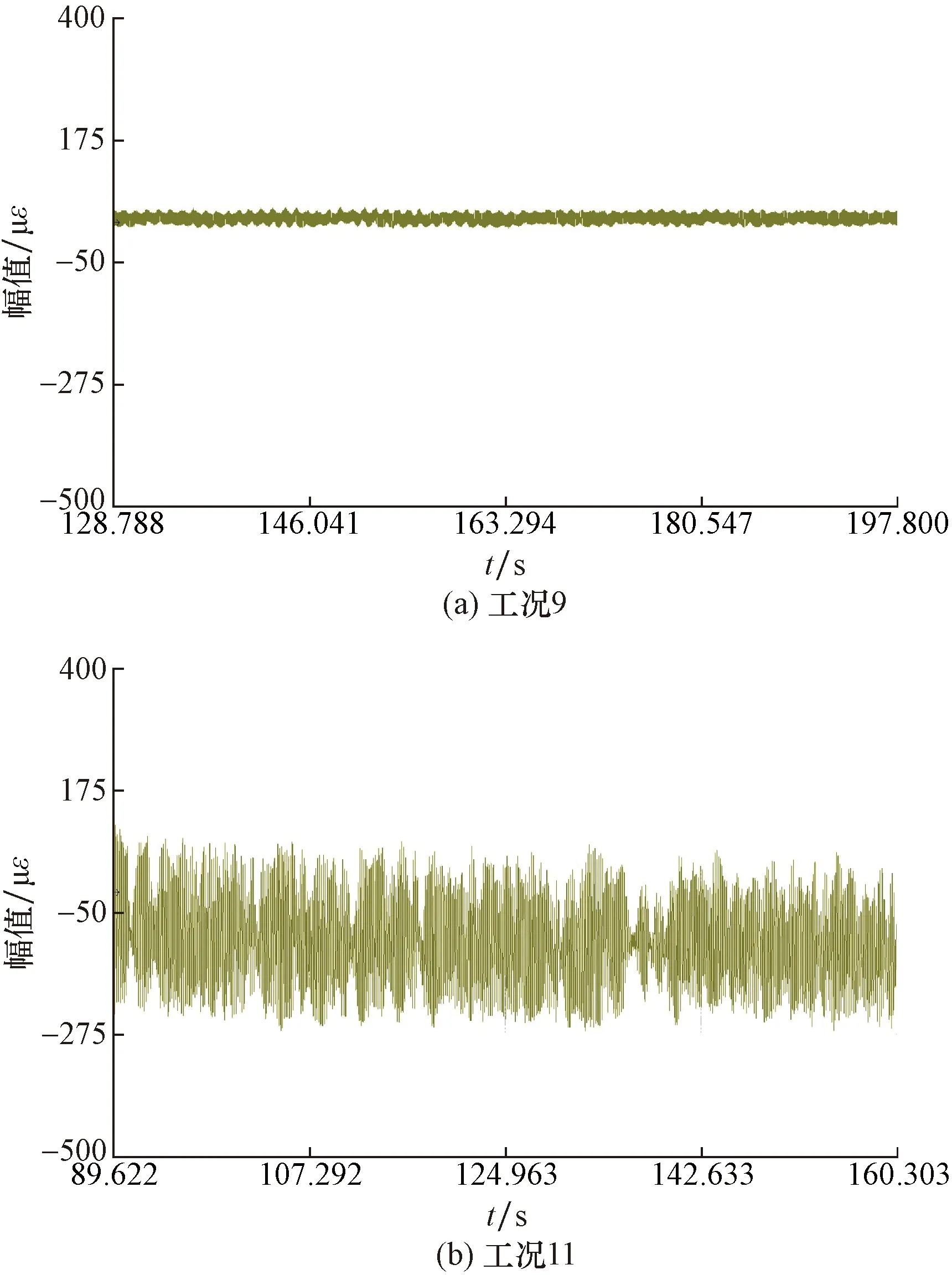
图18 两种工况下PMMA立管Ay点顺流向振动应变时程曲线Fig.18 The microstrain time curve for the two different test case in the flow direction of Ay point

图19 两种工况下PMMA立管By点横流向振动应变时程曲线Fig.19 The microstrain time curve for the two different test case in the cross-flow direction of By point
从图18和图19中可以看出,工况9和工况11的顺流向振动幅值分别为40、387 με,横流向振动幅值分别为40、513 με。说明随着流速的增加,两流向的振动幅值均增大。
4.5 波浪大小对立管顺流向及横流向振动幅值的影响
以工况9和工况10(大波浪为长周期大波高,小波浪为短周期小波高,其他参数相同,且为小顶张力、小流速、大波高、少约束数、小弹性模量的工况)的Ay(顺流向,z=0.9 m)及By(横流向,z=0.9 m)测点数据为例(图20和图21),说明不同波浪周期对立管顺流向及横流向振动的影响情况。大流速时波浪周期影响不明显。
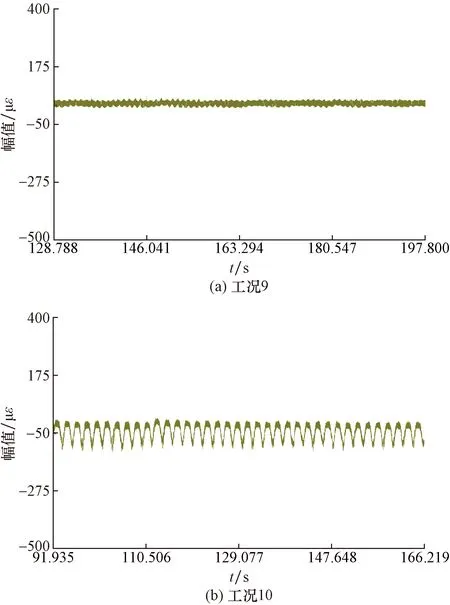
图20 两种工况下PMMA立管Ay点顺流向振动应变时程曲线Fig.20 The microstrain time curve for the two different test case in the flow direction of Ay point

图21 两种工况下PMMA立管By点横流向振动应变时程曲线Fig.21 The microstrain time curve for the two different test case in the cross-flow direction of By point
从图20和图21中可以看出,工况9和工况10的顺流向振动幅值分别为40、134 με,横流向振动幅值分别为40、109 με。说明在其他条件相同的情况下,大波浪作用下立管的振动幅值大于小波浪作用下的立管振动幅值。同时可以看出,小流速下,立管振动的大周期接近于波浪周期,特别是顺流方向。
5 结论
(1)顺流向及横流向两个方向振动幅值均与立管的弹性模量和约束数量成反比,低流速下顺流向和横流向振幅接近,随着流速增加,横流向振幅增长更明显。
(2)在其他条件相同的情况下,S-F约束及增大的顶张力在两个方向均明显限制了立管的振动,特别是在垂直来流方向,直接影响到同流速下是否发生明显的涡激振动现象。
(3)立管的振动频率受波浪因素的影响,大多情况下顺流向振动的频率与波浪的频率一致且波高增大将明显导致立管振动幅值的增大。
(4)流速的增加是立管发生涡激振动的重要因素,随着流速的增加,立管两个方向的振幅明显增大。
