八音盒视频运动音符识别综合实验设计

于 蕾，张 宇，柳守一，汲清波

（哈尔滨工程大学信息与通信工程学院，哈尔滨 150001）

0 引 言

“机器视觉”［1］作为一门综合性创新实验课程，综合了光学［2］、机械自动化、电子信息、计算机软硬件［3］等课程。涵盖专业知识广泛：包括信号处理、计算机视觉、计算机工程等专业知识。“机器视觉”实验课程，有利于将知识融会贯通并应用于实际工程中。

本文针对实验课程实例——“八音盒视频处理”，设计了基于图像处理［4］的视频关键特征检测［5］实验方案。实验实例对象为18 音阶机械八音盒，其运行视频的截图如图1 所示。实验方案，将对实例对象八音盒的运行视频，通过数字图像处理、提取特征等方式，完成乐谱特征提取，将识别到的音符特征表征出来并演奏。

图1 实例对象——八音盒

1 相关原理

八音盒核心部件有（见图1）：①滚轴部、②音板、③储能弹簧。针对给定的八音盒视频，以提取并恢复相应音符信息为目标进行设计。八音盒是由滚轴旋转，滚轴上的凸起拨动音板发声的，包含音符信息的位置集中在2 个区域：②银色不同长度的音板部分和③滚轴上不同位置的凸起。在音符信息变化过程中，音板的明暗变化较弱，易受光源不均匀等外界因素干扰，滚轴部分虽存在明显噪声干扰，却包含更明确的音符特征信息。设计实验针对滚轴部分凸起进行图像处理提取特征，并结合音频频率分析对提取到的音符特征进行恢复。

实验设计的原理包括数字图像处理、信号时域频域分析、乐器数字接口（Musical Instrument Digital Interface，MIDI）编程等技术［6］。

1.1 图像形态学

图像形态学［7-8］也被称作数字形态学，以形态结构单元为工具对图像进行处理。形态学通过不同大小、不同形状存放不同权重的基础结构单元，对整幅图像做平移不变性的计算处理，以达到提取特征、消除噪声、图像映射变换等目的。图像形态学一般对灰度图像或者二值图像进行处理。一类典型的应用是通过形态学运算降低图像干扰噪声，在很大程度上保留图像本身的必要特征［9］。图像形态学的基本运算包括：形态学开操作、形态学闭操作、形态学膨胀和形态学腐蚀［10］。

（1）二值形态学。结构元素是形态学操作中最重要的基本单元，不同的基本单元对图像进行处理会产生截然不同的结果。常用的结构元素形状包括矩形和十字形等。在进行形态学操作时，其基本结构单元被称作形态学算子。形态学算子直接决定了形态学处理的结果。形态学运算的本质是形态学算子在图像上的平移不变性运算，类似于加窗。基本的形态运算包括腐蚀和膨胀。

（2）形态学腐蚀。形态学腐蚀是一种常用的形态学图像处理手段，通过腐蚀操作，可在一定程度上保留目标特征而消除部分噪声干扰。常常与形态学膨胀同时使用。假设用B（x）代表结构元素，对工作空间E中的每一点x，形态学腐蚀运算结果

式中，“⊙”为腐蚀运算符。形态学腐蚀如图2 所示。

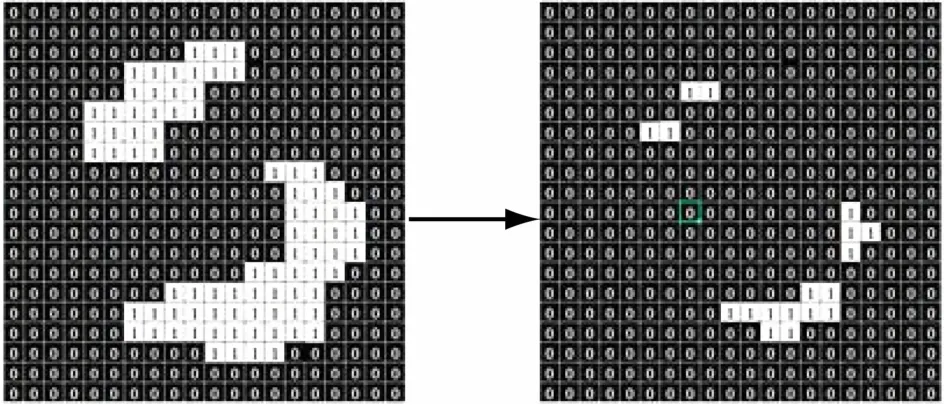
图2 形态学腐蚀

（3）形态学膨胀。与形态学腐蚀相反，形态学膨胀如图3 所示，膨胀运算结果

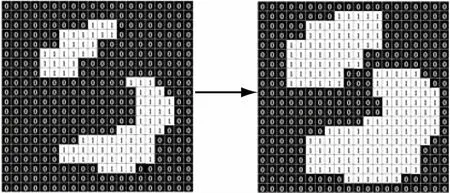
图3 形态学膨胀

式中：“⊕”为膨胀运算符；B（y）为点y位置对应的原素结构；ø为空集。

1.2 音频信号时频分析

傅里叶变换在解决信号时频问题时具有很大的局限性，为解决傅里叶变换不能区分时间尺度上不同频率信息，提出短时傅里叶变换（Short Time Fourier Transform，STFT）［12-13］。其本质是对目标信号与窗函数相乘，分析一段时间内的频谱特性，将窗函数按时间顺序平移计算下一个窗口的频谱特性。在进行STFT的过程中：首先假定一个非平稳信号在窗口内是平稳的，将目标信号x（t）与有限窗函数h（t）相乘再进行傅里叶变换，即可得到窗口时间内频谱，对h（t）在时间轴x上的移动，对信号进行逐段分析得到信号的一组频谱。信号x（t）的STFT定义［14］为

式中，h（τ－t）为h（t）在时间轴τ 上的被动得到的有限窗函数［15］。分别截取小时间段内的短信号做快速傅里叶变换（Fast Fourier Transform，FFT）变换，即可得到信号x（t）的时域频域分析结果。

1.3 MIDI编程

MIDI［16-17］是桌面系统底层封装的应用程序接口（Application Programming Interface，API），通过调用API接口可实现驱动声卡发声，常用于音乐相关项目的开发。不但可播放本地文件，还可通过链接库实现不同音阶的音符播放。

2 音符实时识别系统

系统总体流程如图4 所示，将八音盒运行视频分为2 个部分：视频图像信息和音频信息；图像信息经过右路图像处理部分获取图像特征。音频信息经过左路得到时域频域分析结果，将视频图像特征与音频的时域频域分析结果在时间上匹配，获得不同时刻图像上特征所代表的具体音符（频率）信息，通过MIDI 编程将音乐演奏播放。

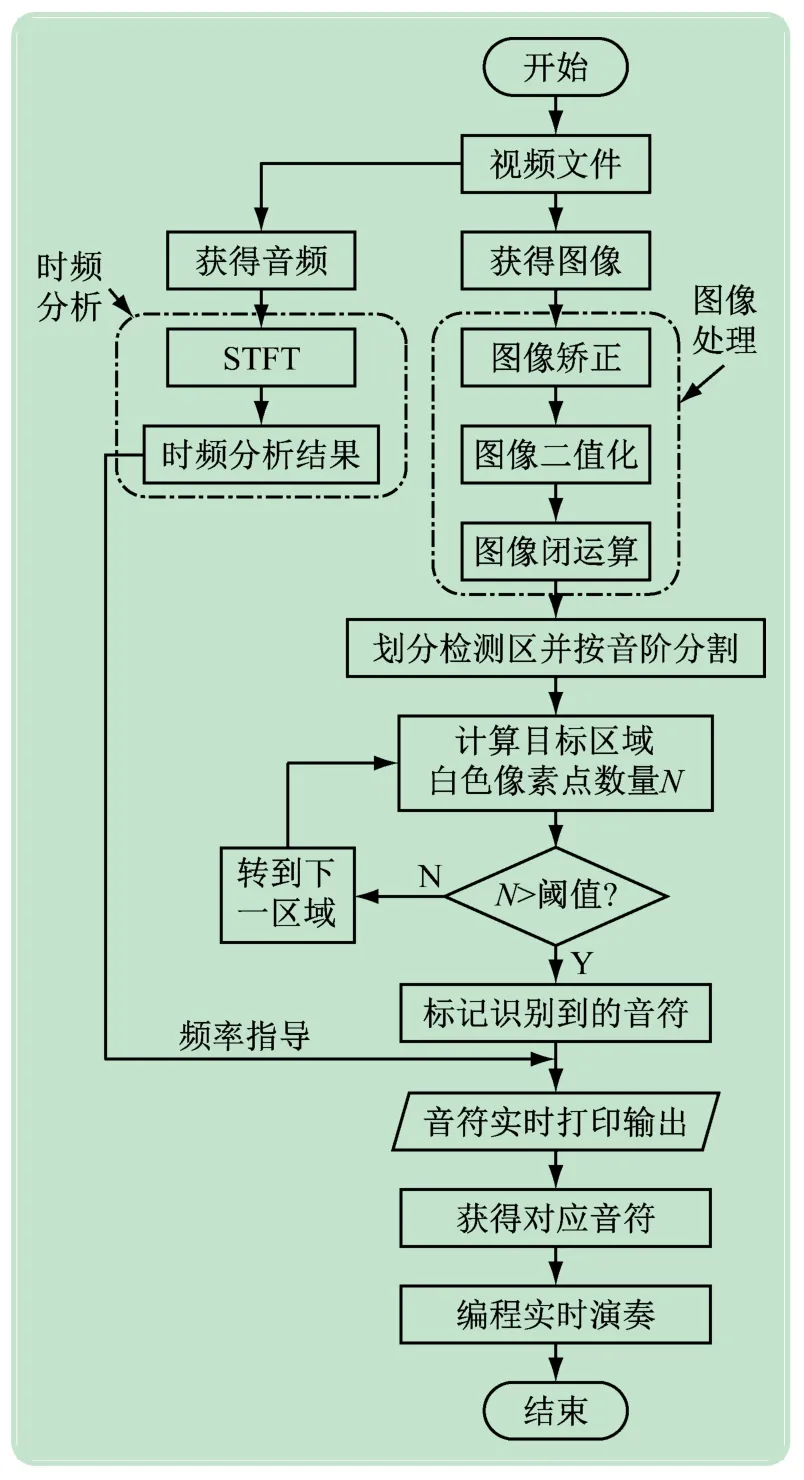
图4 系统总体流程图

2.1 图像处理

视频中图像信息过于复杂，大部分图像对乐谱的识别没有作用。采用提取感兴趣区域（region of interest，ROI）选择包含乐谱信息的部分进行处理。这里选择匀速转动的滚轴区域作为感兴趣区域。

选定感兴趣区域后，从视频中获取每一帧图像并截取感兴趣区域，对每一帧图像进行灰度处理和图像二值化，处理结果如图5 所示。

图5 图像处理过程

由图5（a）、（b）可知，滚轴左右两侧部分存在难以去除的反光干扰噪点，中间部分图像虽然存在部分噪点，但去除相对容易，所以将滚轴轴体中部作为主要分析对象。在图5（b）的二值图像中，存在2 种主要的噪点：滚轴上的固有缺陷产生的小型噪点（下称为小噪点）和接缝处印有型号的钢印造成的大范围噪点（下称为大噪点）。

对不同类型的噪点，采用的去除噪声的手段也不一样。对于小噪点，采用形态学运算的方式，在保留足够有效特征的基础上，去除图像中的小噪点。先利用3 ×2 的矩形算子对图像做开运算去除小噪点，再用1×2 的矩形算子对图像进行膨胀操作，在纵向上弥补开运算对图像特征造成的损失。处理后的图像如图5（c）所示。可看到小噪点被有效去除，大噪点依然存在。对于大噪点，将在后面的音符识别中进行静默过滤操作。通过对大噪点的出现范围及其白色像素数量与阈值比较，当识别到大噪点转动到目标区域时，将音符识别算法静默。

2.2 音符识别

经过图像处理，中间部分只剩大噪点的干扰，在此基础上设计音符识别提取部分。如图6 所示，绘制长条矩形区域，纵向涵盖滚轴18 个音节对应的凸起，横向宽度略大于一个凸起特征。将长矩形18 等分，分别对应不同位置的音符凸起。通过判断每个格子内的白色像素点比率来判定是否有音符特征经过，若当前帧的图像指定格子里存在音符特征，则白色像素比率将会大于阈值，此时将当前帧的目标格子标记为白色。

图6 分区检测过程

在标记音符特征的同时，将特征信息按时间序列绘画并显示，输出音符乐谱特征如图8（b）所示。

2.3 音频信号的时频分析

为获得视频中不同位置音符特征所对应的实际音符（频率），采用对视频的音频信号进行时域频域分析。从视频文件中提取到相应的wav 音频文件，将音频文件输入到程序中。其中时域信号如图7 所示。

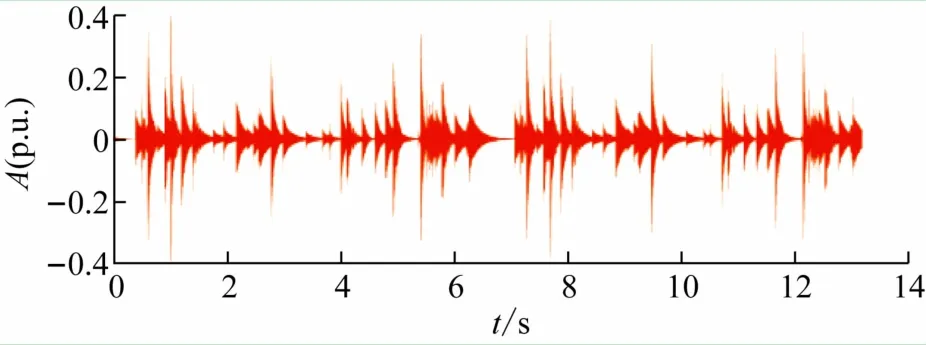
图7 音频时域信号

对音频时域信号进行STFT，得到信号的时频特性，如图8（a）所示，由图可获得各音符的频率。

图8 音符特征与视频特征对比

2.4 获得音符频率

在音符识别和时频分析后，得到音频中的视频图像中的音符信息特征与音频信号的时频特征，分别如图8（a）、（b）所示。其中时频特征包含了每个音符的频率信息，还包含了不同频率的音符出现的时序信息。图8（b）中包含了滚轴上不同位置的音符图像的位置信息以及不同音符出现的时序信息。两幅图的时序信息是存在对应关系，可得图8（b）中每个位置所代表的频率。例如图8（a）、（b）中虚线内为一个周期T，以黑色矩形内信息为例，上下两图之间具有同样的音符时序变化信息，将特征输出一一对应，即可获得视频图像中每个位置的音符的频率。位置序号与音符频率对应关系见表1。

表1 位置序号与音符频率对应关系

由表1 可见，不同序号位置同凸起对应的音符，结合图8（b）即可获得完整的乐谱信息。获取的完整乐谱信息将用于后续的MIDI编程中。

2.5 MIDI编程实现

MIDI编程可发出不同音色的音符和旋律。选择钢琴作为实施演奏的音色乐器。MIDI 编程以一个8位十六进制参数来控制输出音符的音量、音调和音色。以0x00403C90 为例，有效位为后6 位，即0x403C90。其中：0x40 为音量；0x3C 为音调；范围为0x0-0x 7F；0x90 为乐器范围应该是0x90-0x9F。其中，0x99 为鼓类，其余皆为不同音色的钢琴。

在演奏实现中，由表1 中位置与音符对应关系预设到程序内，以图6 右图中小格子内颜色变化为激励信号，当颜色由黑色变白色时，即识别到音符到来，利用MIDI播放当前位置对应的音符。当对视频实时处理，产生实时输出的处理后视频的同时，完成对识别到的乐谱演奏的效果。

3 结 语

本文提供了对八音盒视频通过计算机视觉等方法，从视频中识别当前所演奏的音符，并能以实时演奏和打印输出的2 种方式实现对识别到的音符特征的重现。

本方案的优点：采用的图像处理算法相对简单易于操作，识别音符信息具有较高的准确性，能实时演奏且效果直观等。在其他方面还具有一定的局限性，如：短时傅里叶变换这种时频分析方法，对音频主旋律的频率有很好的解析效果，但由于实际音频中还包括伴奏的旋律，伴奏的信号强度要小于主旋律音符信号，对伴奏旋律音符频率的分析结果存在一定误差。可改进对音频信号的时频分析方法，如采取更高精度的小波变换、滤掉主旋律频率后单独对和音频率进行时频分析等方法，来获得更高的频率精度。