基于虚拟仿真的电力系统暂态过程中的能量分析与计算

2023-08-22李亚龙

实验室研究与探索 2023年5期

田旭，刘岩，李亚龙，杨佳

（中国矿业大学（北京）机电与信息工程学院，北京 100083）

0 引言

稳定性是电力系统运行的基本要求，电力系统暂态稳定是《电力系统分析》课程的重要且难于理解的知识点之一，包括利用等面积定则分析简单电力系统的暂态稳定性以及强行励磁、快关汽门等措施对于暂态稳定性的影响。由于电力系统暂态过程复杂，等面积定则的推导过程十分粗略，学生理解起来比较困难。采用虚拟仿真的方式开展实验研究，既可直观看出暂态过程中发电机各物理量的变化曲线，进行理论分析，同时，还可避免实际实验的安全和高成本，是提高教学效果的有效方法。

张夏恒等［1］利用Matlab／Simulink 软件建立三机九节点系统的仿真模型，研究静止无功补偿器对复杂电力系统暂态稳定性的影响。文献［2］中建立了单机-无穷大系统的仿真模型，研究强行励磁、变压器中性点经小阻抗接地、快关汽门对于暂态稳定的影响。代传波等［3］分析了单机-无穷大系统暂态稳定性的影响因素，并运用小波变换模极大值法精确定位出故障点位置。文献［4］中研究了电力系统暂态过程中，电力系统稳定器，强行励磁对发电机功角、转速、电磁功率以及机端电压的影响。根据目前掌握的文献来看，电力系统暂态过程中加速以及减速过程中的能量计算与比较，损耗能量的计算分析以及暂态过程中的能量守恒问题的研究，还未见报道。

本文利用RT-Lab 实时数字仿真平台［5］，建立单台同步发电机经变压器、输电线路接入无穷大电网的电磁暂态仿真模型，提出暂态过程中加速能量、减速能量以及损耗能量的计算方法。通过定量的计算，精准地验证了单相接地、两相接地短路条件下，电力系统暂态过程中的能量守恒，加深了对等面积定则的理解。研究了强行励磁、快关汽门对电力系统暂态过程中加速、减速能量的影响，分析了它们对于暂态稳定性的影响。

1 电力系统暂态稳定性与等面积定则理论基础

电力系统暂态稳定性通常采用单机-无穷大电网来说明［6］。单机-无穷大系统如图1（a）所示。

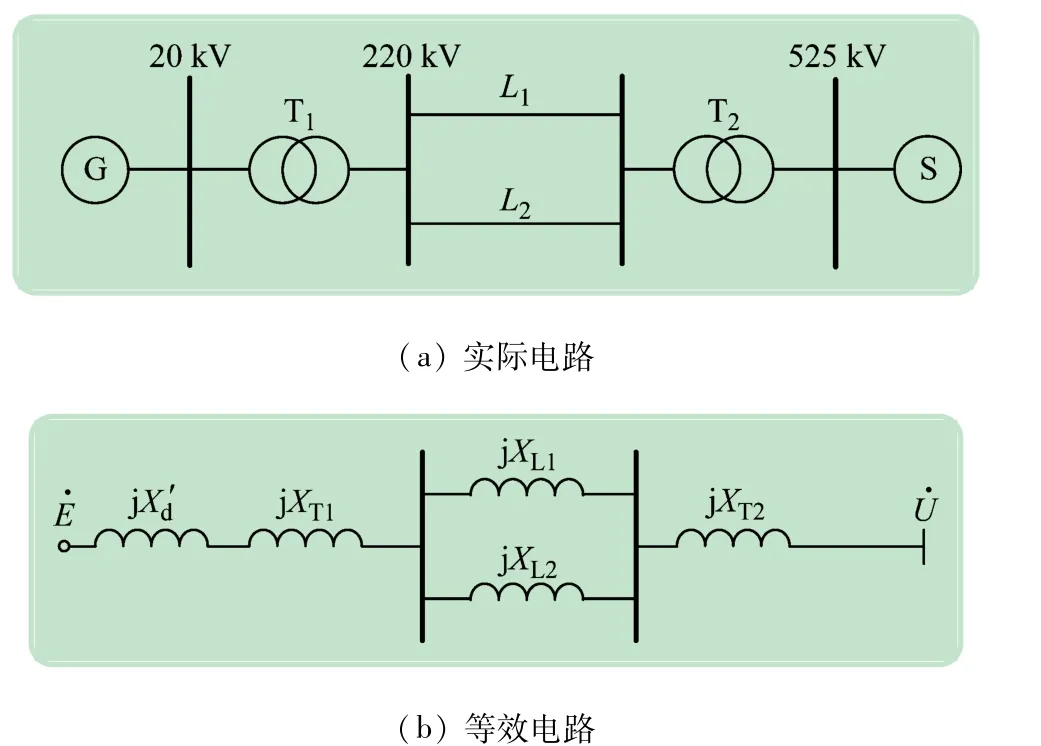
图1 单机-无穷大系统图

在暂态稳定性研究中，通常假设无穷大电网频率恒定为50 Hz，忽略发电机的非周期分量及负序分量，发电机输入机械功率恒定。将发电机用电动势和电抗串联支路来等效，则单机-无穷大电网的等效电路如图1（b）所示。

若系统发生大扰动（例如短路故障）过程中，系统的功率特性曲线如图2 所示。

图2 单机-无穷大电网故障发生前、切除前、切除后的功率特性曲线

图中：PⅠ、PⅡ、PⅢ分别为系统正常运行、故障发生和故障切除后的功率特性；PT为原动机输入的机械功率；δ0、δc、δk分别为故障前稳态条件下、故障切除瞬间、故障切除后系统进入新稳态时的功角值；δm为故障期间功角振荡过程中能达到的最大值。

发电机从系统故障发生前到故障排除后进入新稳态的整个过程可分为以下几个阶段［7-8］：

（1）故障前正常运行。对应图2 中的a点。该点在曲线PⅠ上，对应的功角为δ0，此时原动机输出的机械功率PT＝P0。

（2）故障发生且被切除之前。发电机的运行点瞬间降低到b点，功率特性同样也降低到PⅡ，此阶段发电机的电磁功率小于机械功率，发电机转子一直加速，随着功角δ逐渐增大，运行点由b点向c点移动。

（3）故障切除后。假设发电机功角增大到c点时，故障线路断路器动作，将故障线路切除。发电机的功率特性瞬间变成PⅢ，发电机的输出功率大于机械功率，转子转速降低。但由于此时速度已经高于同步转速，功角δ 还要继续增大。当运行点到达f点时转速降低为同步转速，此时电磁转矩大于机械转矩，转子将继续减速，δ继续减小，运行点沿着功率特性PⅢ由f点向e、k点移动，最终稳定运行于k点。

由于发电机在a点和f点的转速均为同步转速，所以发电机动能没有变化。如果忽略发电机由a点运行到f点的过程中的能量损耗，则加速过程和减速过程的能量之和应该为零，即

经过简单变换可得

按照高等数学中积分的几何意义，式（2）中的左、右两边分别对应图2 中加速过程和减速过程阴影部分的面积，所以式（2）又被称为等面积定则［9］。

等面积定则的理论推导过程忽略了能量损耗，在工程实际以及实验仿真中，能量损耗却不可忽略，所以，必须研究加速过程、减速过程中实际的能量变化过程，并提出能量损耗的计算方法，使学生对暂态过程中能量守恒的理解更加深入。

2 仿真模型的建立与发电机功角计算

根据图1（a）所示单机-无穷大电网搭建的仿真模型如图3 所示。

图3 单机-无穷大系统仿真模型

仿真模型参数设置如下（下标“*”为标幺值）：

发电机P＝660 MW，UN＝20 kV

变压器T1连接方式D11／Yg

S＝730 MVA，20／220 kV，R1*＝0.01，L1*＝0.07，R2*＝0.01，L2*＝0.07。

变压器T2连接方式Yg／Yg

S＝1 000 MVA，220／525 kV，R1*＝0.005，L1*＝0.03，R2*＝0.005，L2*＝0.03。

线路L1和L2三相线路

L10＝0.78 mH／km，L00＝4.126 4 mH／km，R10＝0.01 Ω／km，R00＝0.386 4 Ω／km，C10＝6.79 nF／km，C00＝7.751 5 nF／km，线路长度：100 km。

负荷UN＝20 kV，P＝10 kW。

无穷大电网UN＝525 kV，f＝50 Hz。

需要特别指出的是，RT-Lab仿真平台无法直接测量同步发电机的功角，只能测量稳态下的功角值［10］。所以，需采用计算的方式得到暂态过程中同步发电机的功角。假设故障发生前，稳态时的功角为δ0，则暂态过程中功角的变化量Δδ 应该等于发电机转子角速度ω与发电机端电压角速度（同步角速度）ωN之差的积分，故暂态过程中的功角

按照上式搭建的功角测量模块如图4 所示。

图4 功角测量模型

3 暂态过程中的能量计算方法

3.1 加速以及减速过程中的能量计算

设置图3 所示的RT-Lab 仿真模型的总仿真时间为40 s，仿真步长为10 μs，在用于显示仿真结果的示波器（Scope）中设置每仿真20 个步长保存一个数据，则示波器中每个通道共有200 001 个数据。将仿真中各示波器的结果导入Workspace，其中Scope1、Scope2、Scope3分别是电磁功率、功角、发电机定子电流。在Matlab中编写代码，利用plot函数绘制功率特性曲线，以单相接地短路故障仿真模型为例，代码如下：

代码运行结果如4.1 节中图6 所示。

通过观察g数组的数值，发现第1 051 个数据最接近额定电磁功率的数值，因此数组g以1 051 个数据为分界点，前半段为加速面积，后半段为减速面积。加速面积以及减速面积利用trapz函数进行计算，代码如下。

3.2 暂态过程中的损耗计算

同步发电机的损耗主要是定子损耗［11］，现需将定子电阻的标幺值转化为有名值：

利用3.1 节测得的发电机端口线电流，在Matlab里编写程序，利用trapz函数计算瞬时功率对时间的积分，得到发电机定子电阻在暂态过程中的功率损耗P0，代码如下：

4 不同短路故障条件下的能量守恒

4.1 单相接地短路故障

设定单相接短路故障发生在线路L2上，在L2两端各设置一台断路器。为使发电机在暂态过程功角振荡幅度较大，更好地展示加速面积和减速面积，设定故障发生后0.2 s断路器动作，切除线路L2。仿真中的功角和电磁功率变化曲线如图5 所示。图5（a）的右上部分是仿真时间19.80～20.10 s 的功角曲线放大图，在仿真运行到10 s 时，发电机进入稳态，功角为20.53°，电磁功率为571 MW。仿真时间为20 s时，发生单相接地故障，功角发生振荡，振荡过程中功角峰值为53.80°，仿真时间为20.2 s时，故障被切除，此时的功角为31.49°，接下来功角进行幅值不断衰减的振荡，最终达到新的稳态，发电机稳定状态下的功角为29.96°，电磁功率仍然为571 MW。

图5 单相接地短路故障时的功角、电磁功率变化曲线

图5（b）右下角部分小图是电磁功率曲线在故障发生后的放大图，放大范围是时间t在20～20.52 s的区间（大图中两条蓝色虚线所包含区域），其中20.20 s时故障切除，因此20～20.20 s 区间的功率曲线与额定机械功率围成的面积对应等面积定则中的加速面积，20.20～20.52 s区间的功率曲线与额定机械功率围成的面积对应等面积定则中的减速面积。

将图5（a）中的功角作为横坐标，图5（b）中的电磁功率作为纵坐标，利用本文3.1 节的Matlab 程序绘制出单相接地短路时的功率特性曲线如图6 所示。

图6 单相接地短路功率特性曲线

利用本文3.1 节中的程序计算加速与减速过程中的能量分别为32.428 MJ和28.860 MJ。利用本文3.2节中的程序计算暂态过程中损耗的能量为3.446 MJ。显然，加速过程的能量约等于减速过程的能量与损耗能量之和，满足能量守恒定律。

4.2 两相接地短路故障

设定两相接短路故障发生在线路L2上，故障发生后0.1 s断路器动作，切除线路L2。仿真中的功角和电磁功率变化曲线如图7 所示。图7（a）的右上部分是仿真时间19.80～20.10 s的功角曲线放大图，在仿真运行10 s左右时，发电机的功角已经基本达到稳态值，其值为20.54°，电磁功率为571.40 MW。仿真时间进行到20 s 时，发生两相接地故障，功角值逐渐上升，到达峰值后再减小，甚至低于稳态值，功角的峰值是55.94°。故障在20.10 s 被切除，此时的功角为25.55°，接下来功角曲线进入振荡状态，直到35 s 左右，功角又达到稳态值，其值为29.97°，电磁功率仍然为571.40 MW。

图7 两相接地短路故障时功角、电磁功率变化曲线

图7（b）右下角部分小图是电磁功率曲线在故障发生后的放大图，放大范围是时间t在20～20.47 s的区间（大图中2 条蓝色虚线所包含区域），其中20.10 s时故障切除，20～20.10 s区间的功率曲线与额定机械功率围成的面积对应等面积定则中的加速面积，20.10～20.47 s区间的功率曲线与额定机械功率围成的面积对应等面积定则中的减速面积。

运行3.1 节的Matlab 程序代码绘制出两相短路接地功率特性曲线如图8 所示。利用本文3.1 节中的程序计算加速与减速过程中的能量分别为39.918 MJ和35.524 MJ。利用本文3.2节中的程序计算暂态过程中损耗的能量为3.943 MJ。显然，加速过程的能量约等于减速过程的能量与损耗能量之和，满足能量守恒定律。

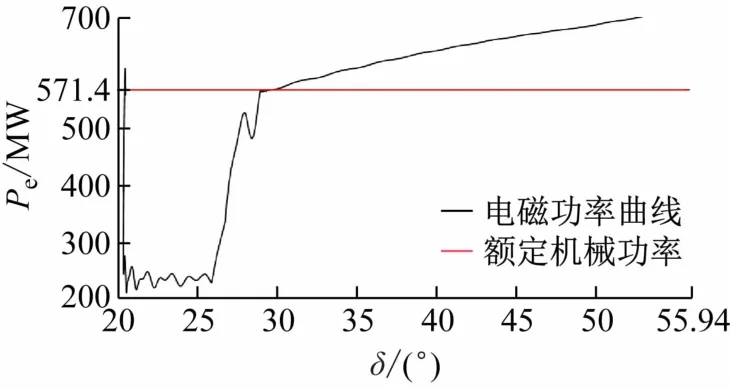
图8 两相接地短路功率特性曲线

5 强行励磁、快关汽门对暂态过程能量的影响

5.1 强行励磁对暂态过程能量的影响

为提高发电机在短路故障时输出的电磁功率，可通过增大励磁电流，提高发电机的电动势来实现，这被称为强行励磁［12-13］。以单相接地短路故障为例，分析强行励磁对于暂态过程中能量的影响。在仿真中设定单相短路故障发生后，励磁电压升高至正常运行时的2 倍，按照上一节给出的方法，绘制出故障过程中的功率特性曲线如图9 所示。

图9 单相接地短路下有无强行励磁的功率特性曲线

由图9 中结果可见，加入强行励磁后，发电机的电磁功率增大，导致的结果是加速面积减小，减速面积增大，显然，加入强行励磁装置有利于提升电力系统的暂态稳定。通过计算可得，加速和减速过程中的能量分别为31.071 MJ、29.935 MJ，损耗的能量为1.124 MJ，满足能量守恒。

5.2 快关汽门

快关汽门是指通过快速关闭主控制阀门或者截止阀［14］，迅速降低汽轮机的机械功率输入，短时间降低发电机组的电功率输出，以适应电力系统在故障后的暂态过程需要，保持事故后电力系统稳定运行［15］。在仿真中设定单相短路故障发生后，快速关闭汽门，发电机输入的机械功率由571 MW变成540 MW，故障过程中的功率特性曲线如图10 所示。